振动压实填石路堤动力响应试验研究

陈爱军，张家生，贺建清，王志斌

（1.中南大学 土木工程学院，长沙 410075；2.湖南工程学院 建筑工程学院，湖南 湘潭 411108；3.湖南科技大学 土木工程学院，湖南 湘潭 411201）

西部工程建设中由于软岩石或硬岩石填料具有强度高、稳定性好、资源多等优点广泛用于铁路、公路路堤。石质路堤压实方法一般采用振动、冲击及强夯补充压实。其中振动压实因效果好、施工成本低、适用范围广等被普遍采用。对振动压实研究主要集中在振动频率、振幅及含水量对压实效果影响［1－2］及特殊土振动压实工艺［3－4］，对由振动压实形成机制及土体动力响应研究较少。据振动及波动理论，振动压路机在土层表面产生振动波，振动波属于固定频率受迫振动并在土体内部以应力波方式传播形成波动。由于土粒振动及相互间应力传递使填料不断被压实。因此，进行填石路堤振动压实的动力响应测试对深入研究振动压实机理具有较强理论意义及实践意义。

针对振动压实路基的动力响应现场测试的相关研究较少见。对路基动力响应研究主要集中于：① 移动车辆荷载及高速列车荷载作用的动力响应［5－6］，此为基于移动载荷对路基周围环境影响角度的研究；② 冲击、强夯击实的动力响应［7－8］，但其产生的瞬时冲击波与振动压实产生的受迫振动有所区别。文献［9］通过对压路机与土壤的整体系统进行仿真建模分析二者的关系；文献［10］利用能量传递原理对振动压实机理进行理论分析及试验。为从动力响应角度深入探讨振动压实机理，本文在风化板岩路堤试验段修筑过程中通过在路基不同深度埋设动土压力盒，对填石路堤的振动压实过程动态响应实时记录，分析竖向及水平动应力传播规律，所得结论可供参考。

1 现场试验方案

现场试验地点为贵州省三穗－黎平高速公路第12标K84＋140～K84＋190处，该段路堤为全填石路堤，中心最大填高30 m，路基顶宽21.5 m，边坡坡度从上至下依次为1：1.5、1：1.75、1：2.0。路堤填料为强风化砂质板岩，抗压强度0.3～0.6 MPa，属软岩，填料颗粒径最大50～60 cm，颗粒级配极不均匀且受开挖方法影响较大。现场用水平分层填筑振动压实，分层厚度40～80 cm。

1.1 动土压力盒埋设方案

振动测试的动土压力盒为双膜电阻应变式动土压力盒，由长沙金码高科技实业有限公司生产，型号JMYJ－1406M，测试量程600 kPa，测试精度3 kPa。动土压力盒埋设在K84＋180左侧距边坡10 m处，埋设前路堤已填筑20 m高。第1层两个动土压力盒间隔50 cm水平放置用于测试竖向动应力；第2、3层两动土压力盒一个水平放置另个竖向放置，分别用于测试竖向、水平动应力。为防止板岩填料在上料过程中对土压力盒的破坏，待上层填料平整后在预埋设位置开挖宽50～80 cm沟，用中粗砂将土压力盒包围后埋设，开始在沟中回填板岩填料，同时将土压力盒数据线用钢管引出避免压断。土压力盒布置见图1，现场埋设见图2。

图1 土压力盒竖向布置图Fig.1 Vertical layout of earth pressure cell

图2 土压力盒现场布置图Fig.2 Site laying diagram of earth pressure cell

1.2 动土压力测试方案

动土压力测试仪器用东华DH5937采集仪，通过与安装有DHDAS动态信号采集分析系统的笔记本电脑相连，实时获取的动土压力变化动态曲线数据保存于电脑硬盘。测试时将振动碾压前的静土压力归零处理，即动土压力实测值不含静土压力，采样频率500 Hz。用陕西中大机械有限公司的YZ32D振动压路机（超大功率压路机）及柳州工程机械有限公司的CLG620振动压路机（重型压路机）现场振动碾压，两台压路机技术参数见表1。填筑碾压第1层时测试其层底动土压力；填筑碾压第2层时测试第1、2层底动土压力；填筑碾压第3、4层时分别测试第1、2、3层底动土压力。测试前该层填料已碾压密实，压路机停在距土压力盒上方10 m外，待土压力盒与采集仪连接好并启动电脑后压路机开始向土压力盒方向振动行驶。压路机正常行驶至距土压力盒上方8 m处开始采集数据，直至压路机在土压力盒上方经过后继续行驶2～3 m停止数据采集。每种工况重复测试两次，若有一次测试波形出现异常，则重测直至其中两次测试结果一致。现场测试见图3。

图3 现场动应力测试Fig.3 Site testing of dynamic stress

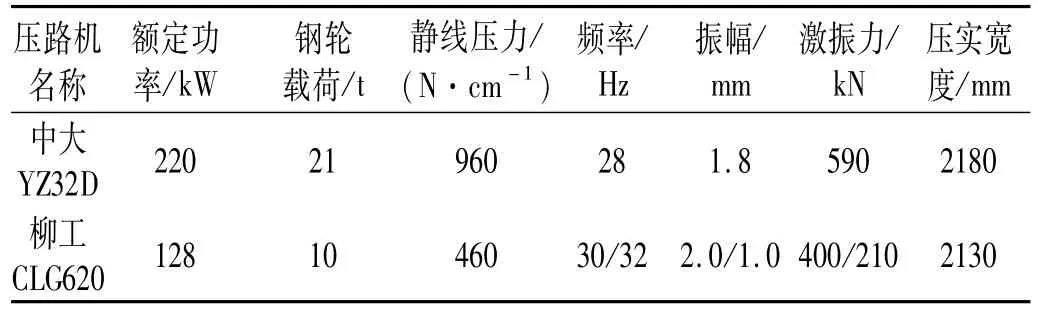
表1 振动压路机参数Tab.1 Parameters of vibratory roller

2 试验结果及分析

2.1 动应力水平传播规律

2.1.1 不同深度动应力水平传播

以第二层底埋设的动土压力盒519745＃、519754＃为例，中大YZ32D压路机分别在碾压第二、三、四层时将土压力盒动力响应较大段时程曲线转换成动应力与距离的关系，便于直观分析应力波水平传播规律。动应力与距离关系见图4。图4（a）、（b）、（c）为碾压第二、三、四层动应力波形。每幅图左、右侧分别表示侧向、竖向动应力与距离之关系，该距离为压力路光轮中心到土压力盒埋置处铅垂高度。由图4看出，动应力表现为某固定频率波形图，据动应力时程曲线峰值段所得频率在25～28 Hz范围内变化，与压路机自身振动频率28 Hz较接近，说明振动波在土中近距离传播时频率基本不变或略有降低。每一振动周期最大振幅是变化的，距土压力盒越近最大振幅越大，而最小振幅为负值且变化较小。在振动波作用下土颗粒由静态变为动态，同时承受动应力加压－卸载的循环过程；动应力足够大时土粒发生疲劳破碎成更小粒径，细小颗粒的增加有利于改善土粒级配并填充粗颗粒间空隙；动应力将克服土粒间摩擦及咬合作用，促使土粒间相互脱离发生位移，排除土中气相，互相楔紧而达到密实状态。

图4（a）土压力盒埋设深度38 cm，侧向动应力、竖向动应力波形图有所差异，即侧向动应力先负后正，最大值均约20 kPa，竖向动应力峰值在距土压力盒100 cm处达－35 kPa，距60 cm时由负变正并显著增大，在土压力盒上方峰值接近200 kPa后逐渐降低并与左侧成对称形态。在压路机碾压过程中表层土受钢轮推挤作用（剪切力）较明显，即钢轮并非完全自行行驶，此剪切力造成钢轮前表层土松散后又被压实，故水平剪应力先于竖向动应力到达表现为负应力（即卸荷）；随竖向动应力的增加而由负转正；侧向动应力先负后正亦为因推挤作用先期到达表现负应力，其后随竖向振动力的到达而表现为正应力。随土层深度增加，钢轮推挤作用影响减小。图4（b）、（c）（对应埋深分别为91 cm，149 cm）中均未发现该明显的推挤作用。

振动轮离土压力盒较远时动应力在0值上下小幅波动，说明振动轮对压力盒影响较小，不会产生土的压实作用。钢轮离压力盒越近，达到某“临界距离”时，无论侧向或竖向动应力均开始线性增加，增加到峰值后表现为对称线性减小，超过“临界距离”在0值附近小幅波动。图4（a）因受水平推挤作用影响难以确定“临界距离”，图4（b）临界距离约 60 cm，图 4（c）临界距离约120 cm。产生临界距离可理解为钢轮振动作用以一定扩散角斜向下扩散，在竖向动应力明显增大位置即可认为竖向振动力斜向下扩散到土压力盒，此时土压力盒距钢轮的水平距离即为“临界距离”。由“临界距离”除以深度的反正切值计算获得压路机碾压的动应力扩散角，本试验中大YZ32D的动应力扩散角在34°～38°之间，柳工 620动应力扩散角在 37°～41°之间。

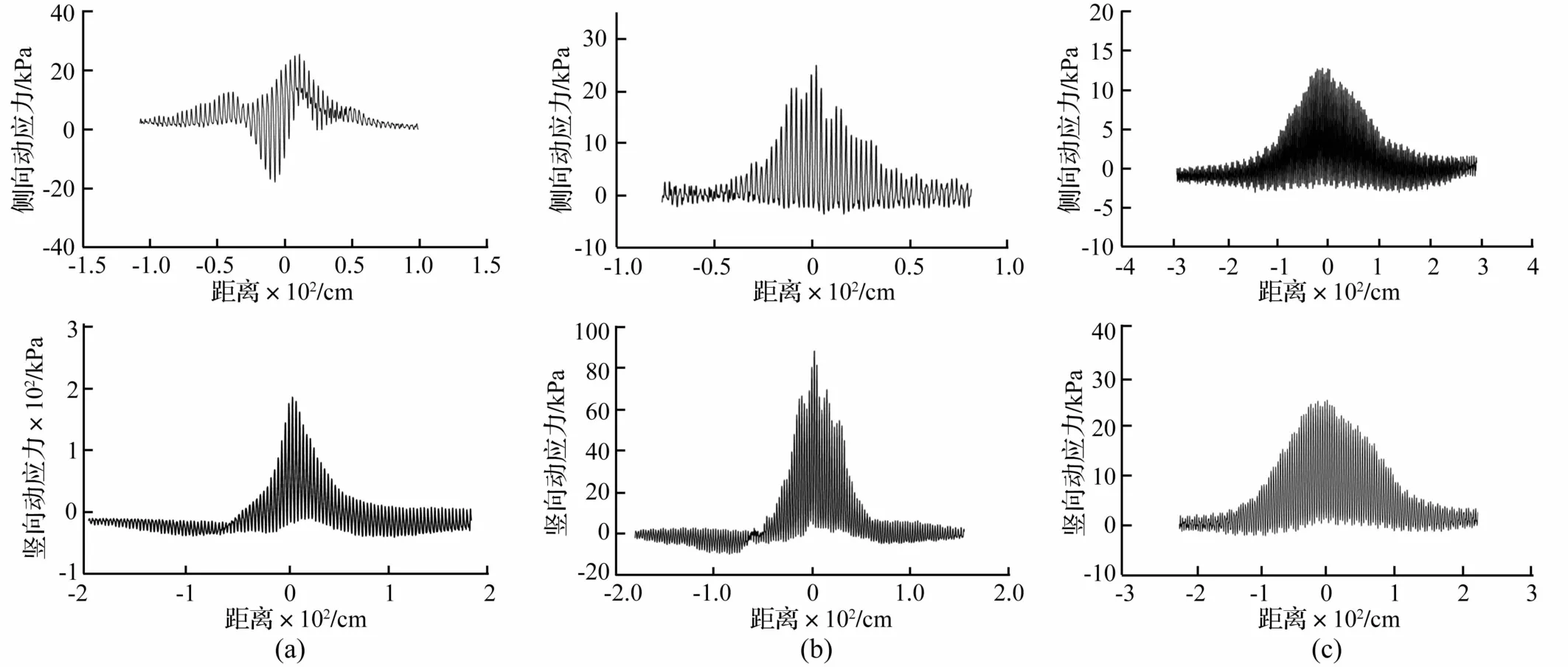
图4 不同深度动应力随水平距离的变化（中大YZ32D）Fig.4 Curve of dynamic stress varying with horizontal distance for different depth

2.1.2 不同压路机动应力水平传播

为比较不同压路机与振动方式在动应力水平方向传播的差异，在中大YZ32D、柳工620强振、弱振碾压第三层时将第三层底土压力盒接收的动应力时程曲线转换成动应力与距离的关系，见图5。由图5看出，同一土压力盒在相同埋深的动应力－距离关系与压路机振动轮重量有关，中大YZ32D振动轮重量21 t，故在土中产生的推挤作用较明显；柳工620振动轮重量10 t，由于对土的推挤作用难以到达层底（深度53 cm），故图5中显示的负动应力不超过－5 kPa。柳工620强、弱振产生的动应力在水平方向传播规律无明显差异，两者“临界距离”均在150 cm附近，振动轮驶离临界距离前动应力在0轴上下波动；驶离临界距离后动应力在0轴以上波动，说明经振动压实后土颗粒间的应力状态较碾压前高。

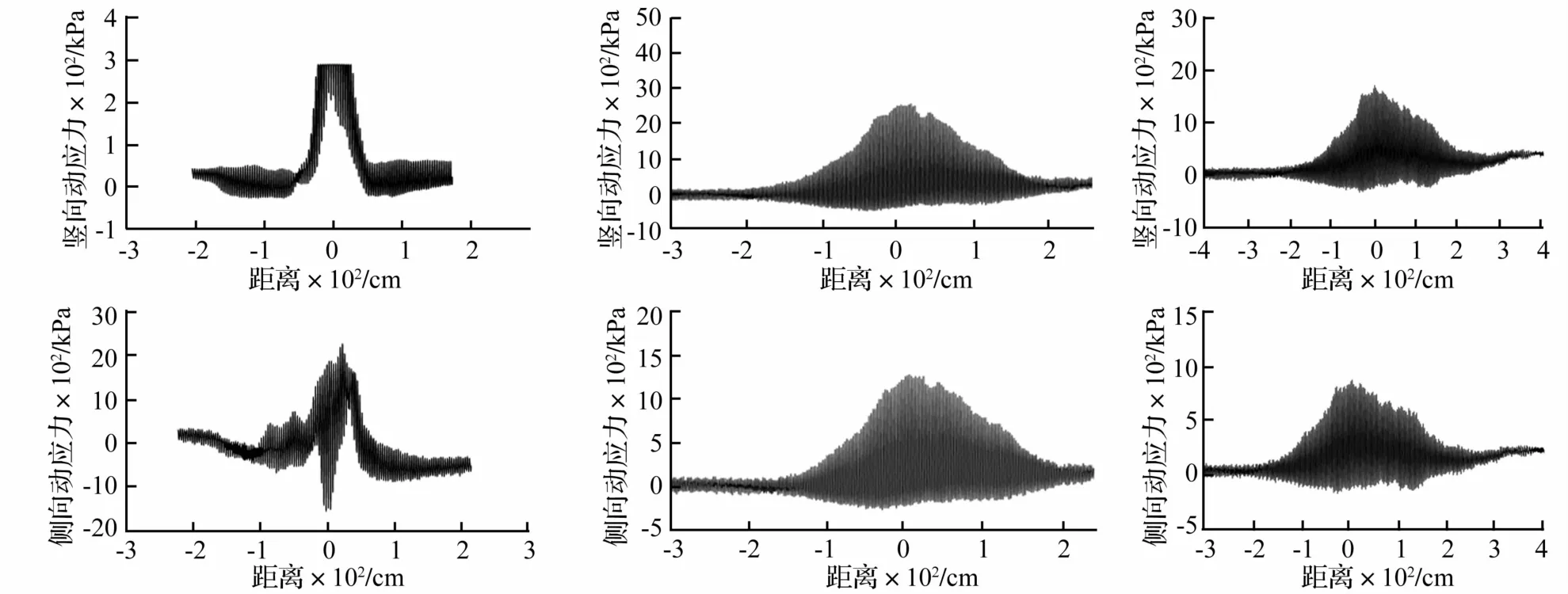
图5 不同压路机的动应力随水平距离的变化Fig.5 Curve of dynamic stress varying with horizontal distance for different roller

2.2 动应力深度衰减规律

2.2.1 动应力沿深度衰减理论推导与验证

据应力波能量衰减理论，应力波在介质中传播时能量会衰减，波强在土中随深度衰减规律为

式中：I为土中h深度波强；I0为初始波强；a为波强衰减系数，与波频率及土体性质有关。

土中某点波强I按正弦函数周期变化，最大值为

式中：ρ为土密度；ω为角频率；A为振幅。

由式（2）知，Imax与振幅A的平方成正比，对弹性介质，在循环荷载初期，动应力σd＝Edεd，每个循环周期的动应变εd幅值等于振幅A，所得波强Imax与每个循环周期动应力幅值σdmax的关系为

结合式（1）、（3），得关系为

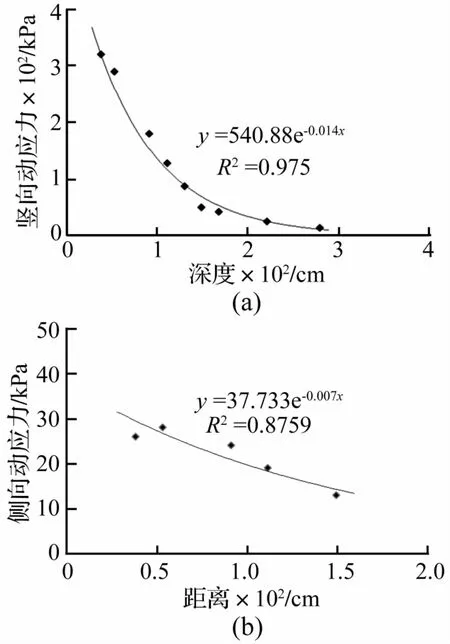
图6 动应力随深度变化曲线Fig.6 Curve of dynamic stress varying with depth

由式（5）知，动应力与深度表现为自然数的指数函数关系，与波强衰减规律一致。

为验证式（5）的正确性，对本次采集的有限数据采用指数函数进行拟合，见图6。由图6看出，动应力由上至下逐渐减小，但竖向动应力衰减速率大于侧向动应力衰减速率。竖向动应力在深度150 cm内迅速衰减，深度149 cm的动应力为50 kPa，仅为深度38 cm处动应力320 kPa的15%；深度超过150 cm后动应力衰减幅度较缓慢，可认为150 cm是中大YZ32D的影响深度。侧向动应力随深度衰减缓慢，由38 cm的26 kPa降低至149 cm的13 kPa，降幅50%，但竖向动应力强度仍明显大于侧向动应力。

据拟合结果（图6），竖向动应力与水平动应力相关性系数R2分别为0.975与0.876，相关性较好。从而由实验角度验证了式（5）的正确性。拟合的竖向动应力衰减系数为0.014，侧向动应力衰减系数为0.007，前者为后者的2倍，说明方向不同动应力衰减速率亦不同。

2.2.2 不同压路机动应力对比及共振探讨

中大与柳工压路机分别在第三、四层顶面碾压时，据不同层位土压力盒测试的动应力最大值获得不同深度动应力值见表2。由表2看出，因振动轮重量及激振力差别，无论柳工强振或弱振，其动应力水平较中大YZ32D小得多。以深度53 cm为例，中大竖向、水平动应力分别为柳工强振的11.1倍及2.1倍；中大竖向、水平动应力为柳工弱振的17倍及3.1倍。由于对土体的压实作用为竖向动应力，当填筑层厚度大于50 cm时，中大YZ32D的压实效果远好于柳工620压路机。

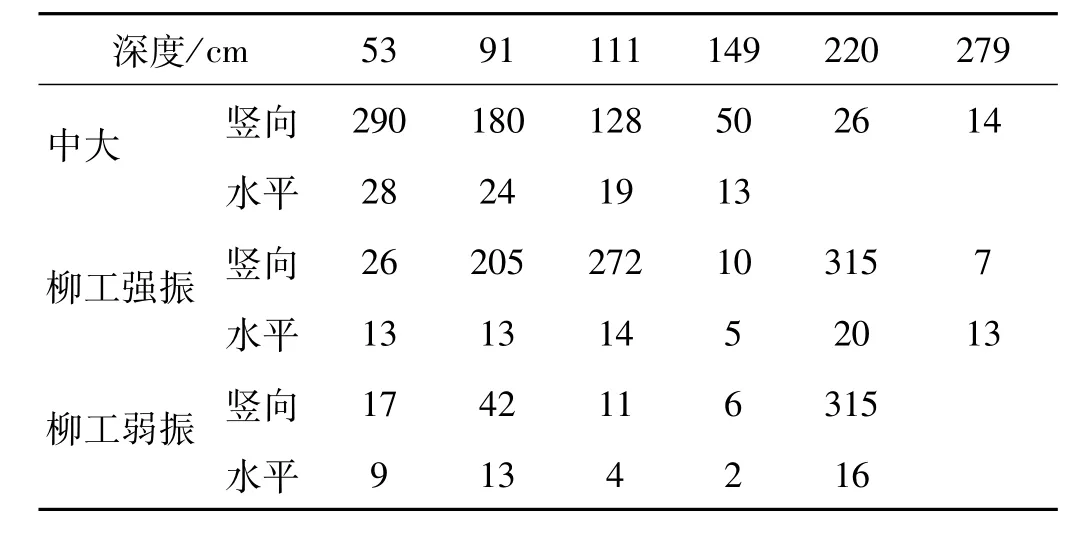
表2 柳工620与中大YZ32D动应力值对比（k Pa）Tab.2 The dynamic stress value contrast between LIUGONG 620 roller and YZ32D roller（kPa）

值得注意的是表2中几个动应力值较异常，如柳工强振在深度91 cm、111 cm、220 cm处的竖向动应力、弱振在深度220 cm处竖向动应力均超过200 kPa且随深度增加而增大。深度220 cm处竖向动应力达315 kPa，为中大YZ32D压路机在此处竖向动应力的12倍。此异常增大现象可能由土体“共振”所致。该“共振”为由激励频率与土体固有频率接近时振幅与应力显著增大的表现。压路机的激励频率为固定的，而土体自身频率与颗粒组成、密度及含水量等有关，在压实过程中填料密度不断增加，“共振”只在土体达到某种临界状态时才会出现。深91 cm、111 cm处柳工强振的动应力与距离关系见图7。由图7看出，柳工强振时91 cm及111 cm动应力波形类似，压路机通过土压力盒上方时并未出现应力明显增大，在所测长度范围内每个周期应力水平相差不大，91 cm处竖向动应力最大值在140～180 kPa之间，111 cm处竖向动应力最大值在200～240 kPa之间。应力最小值为负且相等，91 cm处竖向动应力最小值为－77 kPa，111 cm处竖向动应力最小值为－97 kPa，原因是土压力为测试前设静止状态压力为0，而实际的土压力盒已受到静土压力作用。由此可推算91 cm处竖向静压力77 kPa，111 cm处竖向静压力97 kPa。

2.3 动侧压力系数讨论

侧压力系数表示土中某点水平方向应力与竖向应力之比，能反映地基中水平向应力变化。在地铁、轻轨、基坑工程勘察中通常要求测试静止侧压力系数；但在路堤挡墙填土的振动碾压及隧道、矿井爆破开挖过程结构物安全设计与计算分析时均涉及到水平动应力，而水平动应力可据动侧压力系数计算。动侧压力系数因测试技术复杂及应用理论不成熟，对其研究成果少有报道。

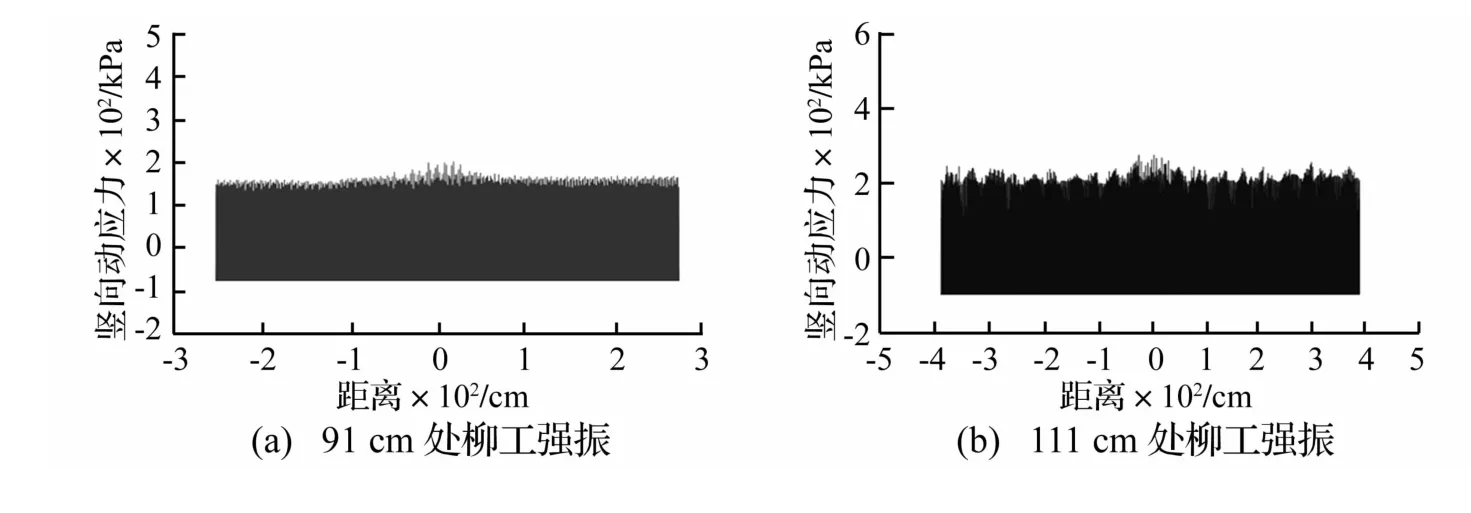
图7 柳工压路机共振波形Fig.7 Resonance wave of LiuGong 620 roller

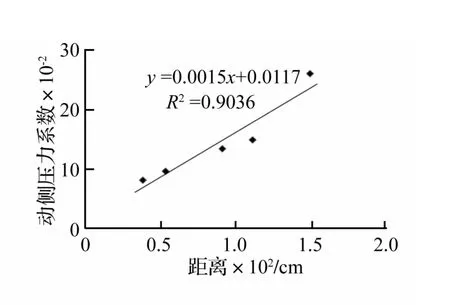
图8 动侧压力系数随深度变化Fig.8 Curve of dynamic lateral pressure coefficient with depth

本文试验在同一水平位置埋设两个动土压力盒分别测试同一深度的水平向、竖向动应力。据不同深度水平向、竖向动应力可计算动侧压力系数Kt，获得Kt与深度之关系，见图8。由图8看出，动侧压力系数随深度的增加而增大，深38 cm时，Kt为0.08，竖向动应力远大于水平向动应力，说明在浅表层土中水平动应力影响较小；深111 cm处Kt为0.15，虽深度增加192%，但其侧压力系数只增加87%；深149 cm时Kt增大到0.26，仍远小于1，即在动应力影响深度范围内水平向动应力所占比重仍较小。本次试验获得5个不同深度的动侧压力系数，采用线性拟合获得系数 R2高达0.903 6，线性相关性较好，说明动侧压力系数并非固定值，而随深度线性增加。

3 结 论

（1）中大YZ32D对表层土产生明显的推挤作用，且产生的水平剪切造成填料松散。振动轮产生动应力在土中以一定角度扩散。中大YZ32D的扩散角为34°～38°，柳工620的扩散角为37°～41°。

（2）据波动理论推导获得动应力在土中的衰减规律，即动应力随深度以自然数指数函数衰减，试验数据亦验证该规律的正确性。竖向动应力衰减速率快于水平动应力衰减。

（3）深度50 cm以下，柳工620产生的竖向动应力远小于中大YZ32D，两者产生的水平动应力相差约1倍；柳工620强振及弱振会在土中局部产生共振。而共振只在土体密度及颗粒级配达到某临界状态时才会发生，本试验测试中大YZ32D未发现共振现象。

（4）据不同深度的水平及竖向动应力实测值，计算获得动侧压力系数在0.08～0.26之间，且随深度增加线性增大。

［1］姚运仕，冯忠绪，董秀辉，等.多频合成振动压实的机理［J］.长安大学学报（自然科学版），2006，26（1）：90－93.YAO Yunshi，FENG Zhongxu，DONG Xiuhui， et al.Mechanism of multi frequencies vibrating compaction［J］.Journal of Changpan University（Natural Science Edition），2006，26（1）：90－93.

［2］Minaev O P.Development of vibratory method for soil compaction during construction［J］.Soil Mechanics and Foundation Engineering，2011，48（5）：190－195.

［3］杨人凤，曾家勇，林冬，等.风积沙压实机理及压实特性［J］.长安大学学报（自然科学版），2011，31（4）：22－26.YANG Renfeng，ZENG Jiayong，LIN Dong， et al.Compacting mechanism and features of aeolian sands［J］.Journal of Changpan University（Natural Science Edition），2011，31（4）：22－26.

［4］申爱琴，郑南翔，苏毅，等.含砂低液限粉土填筑路基压实机理及施工技术研究［J］.中国公路学报，2000，13（4）：12－15.SHEN Aiqin，ZHENG Nanxiang，SU Yi，et al.Study of compacting mechanism and construction technology of filling road bed with bearing sand silt of low liquid limit［J］.China Journal of Highway and Transport，2000，13（4）：12－15.

［5］聂志红，李亮，刘宝琛，等.秦沈客运专线路基振动测试分析［J］.岩石力学与工程学报，2005，24（6）：1067－1071.NIE Zhihong，LI Liang，LIU Baochen，et al.Testing and analysis on vibration of subgrade［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（6）：1067－1071.

［6］郭志广，魏丽敏，何群，等.武广高速铁路无砟轨道路基动力响应试验研究［J］.振动与冲击，2013，32（14）：148－153.GUO Zhiguang，WEI Limin，HE Qun，et al. Tests for dynamic response of ballastless track subgrade of wuguang highspeed railway［J］.Journal of Vibration and Shock，2013，32（14）：148－153.

［7］张锋.深季节冻土区重载汽车荷载下路基动力响应与永久变形［D］.哈尔滨：哈尔滨工业大学，2011.

［8］贾宝印，楼梦麟，宗刚，等.车辆荷载引起地面振动的实测研究［J］.振动与冲击，2013，32（4）：10－14.JIA Baoyin，LOU Menglin，ZONG Gang，et al.Field measurements for ground vibration induced by vehicle［J］.Journal of Vibration and Shock，2013，32（4）：10－14.

［9］Pietzsch D，Poppy W.Simulation of soil compaction with vibratory rollers［J］.Journal of Terramechanics，1992，29（6）：585－597.

［10］Gray W A，Rhodes G T.Energy transfer during vibratory compaction of powders［J］.Powder Technol，1972，6：271－281.