裂纹参数对航空发动机叶片频率转向特性影响研究

张俊红，杨 硕，刘 海，2，林杰威

（1.天津大学 内燃机燃烧学国家重点实验室，天津 300072；2.中国汽车技术研究中心，天津 300162）

叶片作为航空发动机关键零件承担能量转换重任，工作环境恶劣、受载复杂，除受离心载荷、气动载荷及振动载荷外，亦受高温、腐蚀影响，疲劳断裂故障常见。工作中出现裂纹不仅影响发动机性能，且高速脱离的断裂叶片对转子系统其它部件或机匣的安全造成严重威胁［1－3］。裂纹萌生及扩展会改变叶片原有振动特性，伴随以频率转向、振型转换为主要特征的耦合振动。不同长度、位置的裂纹对叶片频率、振型影响规律不同，即使相同长度、位置对叶片不同阶模态影响亦不同。因此，研究裂纹叶片振动特性变化规律，对叶片裂纹故障早期预测及诊断十分重要［4］。

频率转向指系统特征值轨迹随某些系统特性参数先汇聚但不交叉再分离现象［5］，并广泛存在于工程振动中。Marugabandhu等［6］分析转速引起的叶片频率转向及振型转换特性；王建军等［7］通过有限元法讨论旋转叶片多阶模态相互耦合导致的复杂频率转向及振型转换问题；任兴民等［5］基于薄板弯曲理论，采用梁函数组合法分析叶片展弦比对频率转向特性影响规律；Kenyon等［8］分析航空发动机叶盘失谐对频率转向及振型转换特性影响；Vincenzo等［9］分析斜拉桥系统中因锁链位置不同引起的频率转向问题；Lopez等［10］研究轮胎转速导致的频率转向特性；Satio等［11］以悬臂板为研究对象，分析裂纹参数变化引起的频率转向及振型转换。

航空发动机叶片几何形状复杂且曲线变化较大，振动特性研究困难，Rao等［12］使用Timoshenko梁理论研究带初始扭转角及初始锥度的旋转梁振动特性；Witek等［13］通过有限元与试验结合方法验证振动为叶片失效主因；Kuang等［14］分析裂纹对旋转叶盘振动局部化影响；丁镇军等［4，15］基于有限元法分析裂纹形状、深度、位置等对叶片固有频率影响；Shih等［16］应用Galerkin法研究周期载荷激励下含裂纹板振动不稳定及非线性响应特性。大量成果中，对叶片疲劳破坏为多阶模态振型联合作用研究较少。本文以裂纹叶片为基础，研究裂纹参数对多阶模态振型影响规律，分析模态特征中频率转向、模态耦合及振型转换特性，拟通过试验模态技术建立叶片精准有限元模型，分析不同裂纹长度、位置对叶片固有振动及受迫振动影响规律，探讨裂纹参数引起叶片频率转向及振型转换问题，为航空发动机叶片疲劳破坏机理研究及故障诊断提供理论帮助。

1 结构模态分析理论

模态是结构的固有振动特性，每阶模态的特定固有频率、阻尼比及振型由计算或试验分析获得，计算或试验分析过程称模态分析，此为结构动态设计及设备故障诊断的重要方法及各类动力学分析基础［17］。研究结构各阶主要模态振动特性可充分了解结构参数对固有频率、模态振型影响规律，进一步探索结构参数变化引起的频率转向及振型转化特性。

对多自由度振动系统，其弹性结构动力学求解可据达朗贝尔原理推导动力平衡方程，即

式中：［M］为结构整体质量矩阵；［C］为结构整体阻尼矩阵；［K］为总体刚度矩阵；｛｝，｛｝，｛u｝，｛F｝分别为系统各节点加速度响应、速度响应、位移响应及载荷向量。

对式（1）进行拉氏变换，引入模态坐标｛q｝，解耦得系统方程组为

式中：Mi，Ci，Ki分别为系统模态质量、模态阻尼、模态刚度；n为刚度矩阵K的维数，即结构系统自由度数；ωi为第i个特征值，即第i阶固有频率；i为第i个模态振型。

2 叶片数值分析模型

用FEM软件建立典型航空发动机旋转叶片有限元模型，见图1（a）。叶片材料Ti－6Al－4V钛合金，弹性模量 E＝110 GPa，密度 ρ＝3 100 kg／m3，泊松比 μ＝0.3。对叶片进行数值模态分析，约束叶片根部模拟真实叶片所受位移约束，计算叶片约束模态下固有频率特征。为验证叶片有限元模型的正确性，使叶片仿真模型与实际叶片动态特性一致，对实际叶片进行模态试验，见图1（b），并与模态试验结果进行对比，模态频率计算、试验结果见表1。由表1看出，采用有限元法所得计算频率与试验频率相差较小，表明叶片有限元模型精度满足要求，可进行下一步分析。

图1 叶片模型Fig.1 Blade model

表1 叶片模态频率计算值与试验值对比Tab.1 Comparison of blade frequencies between calculation and measurement

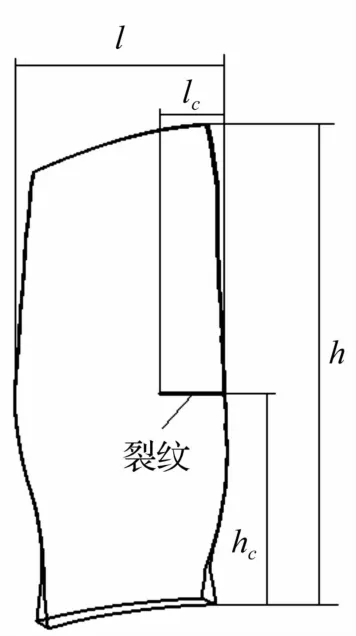
图2 裂纹叶片分析模型Fig.2 Blade crack analysis model

在叶片模型基础上构建裂纹叶片数值分析模型见图2。研究叶片裂纹参数，包括裂纹长度、位置对叶片固有、受迫振动影响规律。设裂纹沿叶片弦向扩展，h为叶片高度，hc为裂纹距叶根距离，l为叶片宽度，lc为裂纹长度。定义裂纹长度与叶片宽度比值（lc／l）为裂纹长度比，表征裂纹相对长度；定义裂纹高度与叶片高度（hc／h）比值为裂纹高度比，表征裂纹相对位置。

裂纹萌生及扩展会改变叶片原有振动特性，并伴随频率改变及振型转换，不同长度、位置裂纹对叶片频率、振型影响规律不同。

3 裂纹长度对叶片频率转向特性影响

3.1 固有振动特性研究

为分析裂纹长度对叶片频率转向特性影响规律，裂纹位置选择较关键。通过应力计算知A点应力最大，易出现疲劳裂纹，选A点为裂纹源，见图3。此处为叶片气流出口，裂纹高hc／h＝0.1，裂纹相对长度取值0≤lc／l＜0.98，计算分析不同裂纹长度引起的频率转向及振型转化。前10阶固有频率与裂纹长度关系曲线计算结果见图4。由图4看出，随裂纹长度的增加固有频率均呈减小趋势，此为裂纹扩展导致叶片刚度减小所致。随裂纹长度变化，叶片表现出频率转向、模态耦合及振型转换等特性（图中圆圈处）。随裂纹长度增加纯弯曲模态固有频率降低较慢，如6、9阶模态；扭转模态及带扭转耦合模态固有频率降低较快，如7、10阶模态，此即造成频率转向原因；研究发现频率转向一般发生在弯曲模态与弯－扭耦合模态之间，单纯弯曲模态间与扭转模态间不会出现频率转向；在频率转向区附近，两阶模态均为复合模态振型。

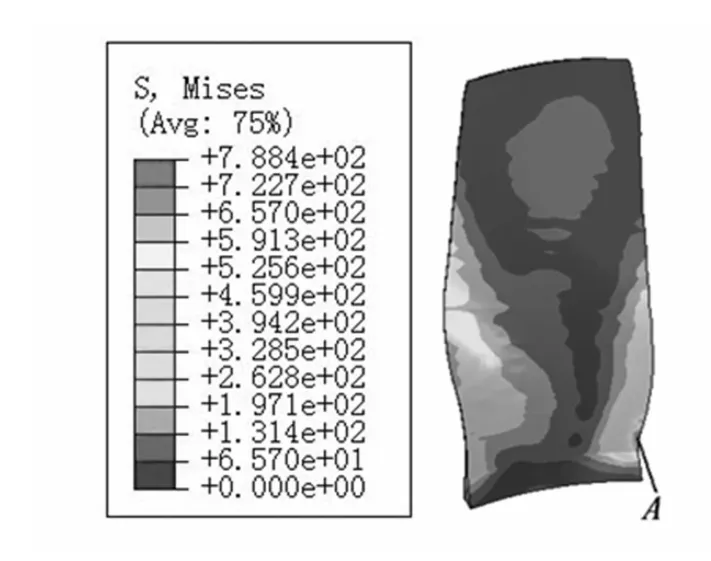
图3 叶片应力分布云图Fig.3 Blade stress distribution

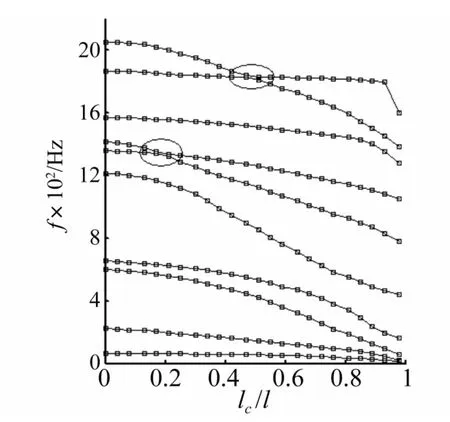
图4 裂纹长度对固有频率影响Fig.4 Crack length compared with natural frequency

图5 第6、7阶频率曲线、模态振型Fig.5 Frequency veering and mode shape of 6 and 7 mode varying with crack length

频率转向本质为模态间振动耦合与振型转换。随裂纹长度变化叶片第6、7阶模态频率曲线及典型位置模态振型见图5。由图5看出，裂纹长度较小时第6阶模态为3弯振型，第7阶模态为3弯1扭振型。随裂纹长度增加第6、7阶模态之间频率线较接近，裂纹相对长度lc／l＝0.2时最接近，之后发生分离，表现为频率曲线间转向。经频率转向区后第6、7阶模态发生互换，第6阶模态变为3弯1扭振型，第7阶模态变为3弯振型，在转向区域，两阶模态均为弯－扭复合振型。叶片第9、10阶模态间同样存在频率转向、振型转换。

3.2 受迫振动特性研究

叶片受迫振动分析可模拟叶片受外界冲击作用时叶片响应。在叶尖中间节点叶面法向施加1 N冲击力，分析裂纹长度变化对叶片受迫振动特性影响。选裂纹相对长度比 lc／l＝0、0.17、0.34、0.51、0.68、0.85时，叶尖节点受迫振动响应的1阶模态频率随裂纹相对长度变化趋势见图6。由图6看出，随裂纹长度增加共振频率逐渐减小，裂纹长度越长，频率降低趋势越快。

图6 裂纹长度对1阶模态受迫振动响应影响Fig.6 1 Mode forced vibration response varying with crack length

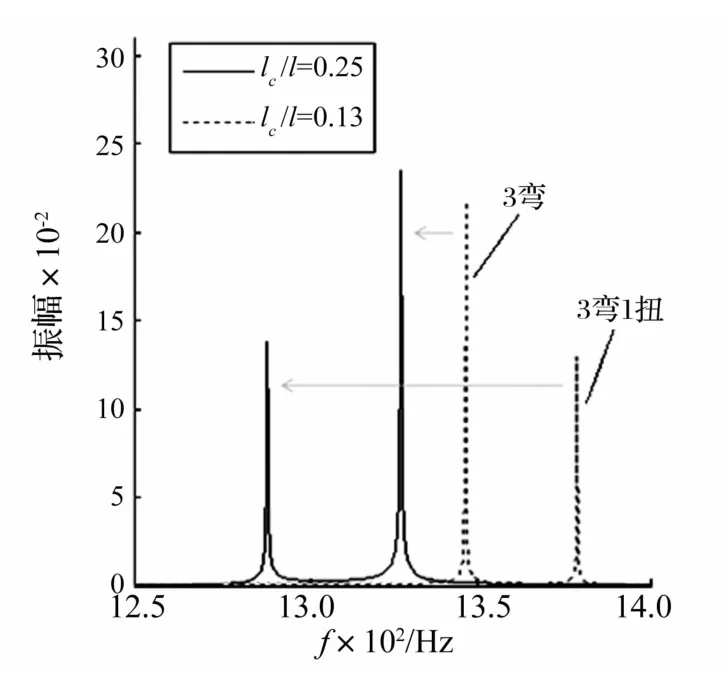
图7 裂纹长度对6、7阶模态受迫振动响应影响Fig.7 Crack length compared with 6 and 7 mode forced vibration response

图8 裂纹位置对固有频率影响Fig.8 Natural frequency varying with crack location

图 7为裂纹相对长度 lc／l＝0.13、0.25时叶片第6、7阶模态受迫振动响应。其中右边虚线裂纹长度比lc／l＝0.13，左边实线裂纹长度比 lc／l＝0.25。由图 7看出，随裂纹长度增加3弯模态频率下降较慢，3弯1扭模态频率下降较快，两者之间完成频率转向及振型转换。

4 裂纹位置对叶片频率转向特性影响

4.1 固有振动特性研究

固定裂纹长度不变，研究裂纹相对位置对叶片频率转向特性影响规律。考虑叶片边缘受外物损伤影响易出现凹坑、缺口，形成疲劳裂纹，因此分析裂纹源选叶片进气边。研究裂纹相对长度lc／l＝0.5、相对高度为0≤hc／h＜0.95时，不同裂纹位置引起的频率转向及振型转化。前10阶固有频率计算结果见图8。由图8看出，裂纹位置引起的频率变化较复杂。

图9为叶片前3阶弯曲模态频率随裂纹位置变化示意图。由图9看出，距叶根35%处裂纹对叶片1阶弯振影响较大，距叶根10%、60%处裂纹对叶片2阶弯振影响较大，距叶根30%、75%处裂纹对叶片3阶弯振影响较大。此因3阶模态对应振型不同所致。裂纹处于某阶模态振型节点附近时，对该阶频率影响较大。由于叶片根部较厚，且存在不规则扭转，因此振型节点不在叶片径向的等分处。

裂纹较长时，裂纹位置变化也会引起频率转向、模态耦合及振型转换特性。图10为第9、10阶模态频率曲线及模态振型。由二图看出，裂纹位置较低时，9、10阶模态分别为4弯、4弯1扭振型。随裂纹位置升高两阶模态变为4弯1扭、4弯振型；在转向区域，两阶模态均为弯－扭复合模态。

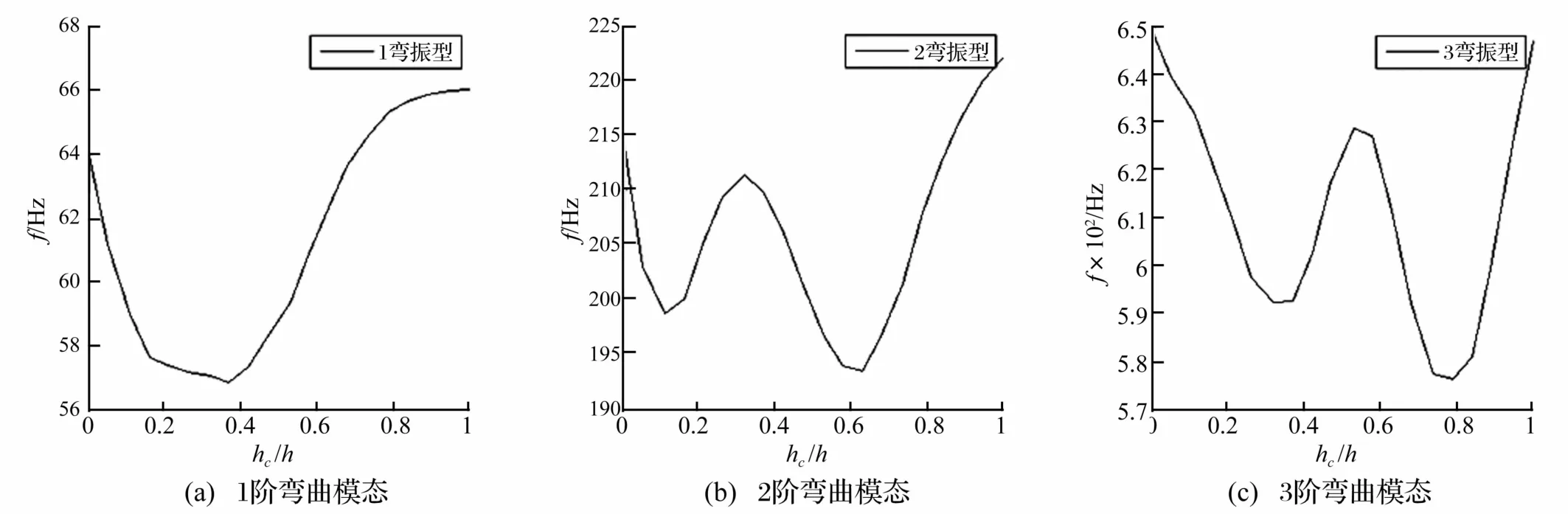
图9 裂纹位置对弯曲模态频率影响Fig.9 Bending mode natural frequency varying with crack location

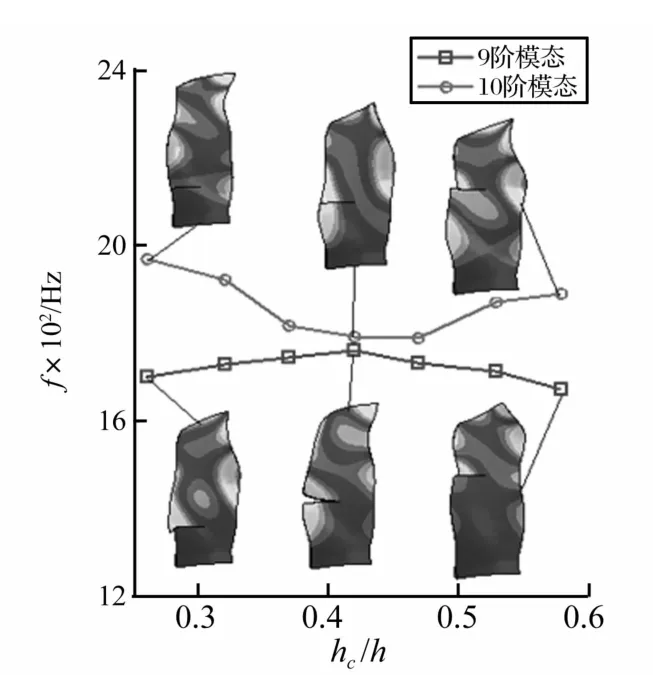
图10 第9、10阶频率曲线及模态振型Fig.10 Frequency veering and mode shape of 9 and 10 mode varying with crack location

图11 裂纹位置对1阶模态受迫振动响应影响Fig.11 Crack location compared with 1 mode forced vibration response

4.2 受迫振动特性研究

选裂纹相对位置分别为 hc／h＝0、0.32、0.64、0.96，分析叶尖节点随裂纹长度变化。1阶模态受迫振动响应曲线见图11。由图11看出，随裂纹高度比增大，叶片1阶模态共振频率先降低后升高，说明裂纹出现在某阶振型节点附近时会对该阶模态影响较大。裂纹位置对叶片振动影响更复杂，与裂纹长度相比，通过振动判断叶片裂纹位置更困难。

图12为裂纹高度比 hc／h＝0.37、0.47时叶片第9、10阶模态受迫响应曲线，其中虚线为裂纹位置比hc／h＝0.37，实线为裂纹高度比 hc／h＝0.47。由图 12看出，随裂纹位置增加4弯模态频率增加，4弯1扭模态频率下降，两者之间完成频率转向及振型转换。

5 结 论

本文以航空发动机裂纹叶片为基础，研究叶片裂纹相对长度及位置参数变化对固有、受迫振动特性的叶片频率转向特性影响，结论如下：

（1）分析裂纹长度对频率特性影响发现，裂纹存在会降低叶片频率，但在裂纹扩展初期频率大小下降较慢。

（2）裂纹长度较小时，裂纹位置变化对频率影响较小，由固有频率确定裂纹位置较困难。裂纹位于模态振型节点时对模态频率变化影响较大。

（3）裂纹长度增加、位置变化均会使叶片出现频率转向、振型转换特性，导致叶片同阶振动模态在裂纹长度、位置不同时模态振型不同。

（4）频率转向一般发生在弯曲模态与弯扭耦合模态之间；在频率转向区附近，两阶模态均为复合模态振型。

［1］Poursaeidi E，Salavatian M.Failure analysis of generator rotor fan blades［J］.Engineering Failure Analysis，2007，14（5）：851－860.

［2］Poursaeidi E，Aieneravaie M，Mohammadi M M.Failure analysis of a second stage blade in a gas turbine engine［J］.Engineering Failure Analysis，2008，15（8）：1111－1129.

［3］Bhaumik SK，Sujata M，Venkataswamy M A，et al.Failure of a low pressure turbine rotor blade of an aeroengine［J］.Engineering Failure Analysis，2006，13（8）：1202－1219.

［4］丁镇军，纪国宜.基于有限元法的疲劳裂纹叶片振动特性研究［J］.机械科学与技术，2010，29（10）：1385－1388.DING Zhenjun， JI Guoyi. A study of the vibration characteristics of a blade with fatigue crack based on finite element method［J］.Mechanical Science and Technology for Aerospace Engineering，2010，29（10）：1385－1388.

［5］任兴民，南国防，秦洁，等.航空发动机叶片“频率转向”特性研究［J］.西北工业大学学报，2009，27（2）：269－273.REN Xingmin，NAN Guofang，QIN Jie，et al.Studying frequency veering characteristics of aircraft engine blade with beam function combination method［J］. Journal of Northwestern Polytechnical University，2009，27（2）：269－273.

［6］Marugabandhu P，Griffin J H.A reducedorder model for evaluating the effect of rotational speed on the natural frequencies and mode shapes of blades［J］.ASME JEng Gas Turbine Power，2003，125：772－776.

［7］王建军，卿立伟，李其汉.旋转叶片频率转向与振型转换特性［J］.航空动力学报，2007，22（1）：8－11.WANG Jianjun， QING Liwei， LI Qihan. Frequency veering and mode shape interaction for rotating blades［J］.Journal of Aerospace Power，2007，22（1）：8－11.

［8］Kenyon JA，Griffin JH，Kim NE.Frequency veering effects on mistuned bladed disk forced response［J］.Journal of Propulsion and Power，2004，20（5）：863－870.

［9］Gattulli V，Lepidi M.Localization and veering in the dynamics of cablestayed bridges［J］.Computers and Structures，2007，85（21／22）：1661－1678.

［10］Lopez I，Doorn R R J J，Steen R，et al.Frequency loci veering due to deformation in rotating tyres［J］.Journal of Sound and Vibration，2009，324（3／5）：622－639.

［11］Satio A，Castanier M P，Pierre C.Estimation and veering analysis of nonlinear resonant frequencies of cracked plates［J］.Journal of Sound and Vibration，2009，326（3／5）：725－739.

［12］ Rao S S，Gupta R S.Finite element vibration analysis of rotating Timoshenko beams［J］.Journal of Sound and Vibration，2001，242（1）：103－124.

［13］Witek L.Experimental crack propagation and failure analysis of the first stage compressor blade subjected to vibration［J］.Engineering Failure Analysis，2009，16（7）：2163－2170.

［14］Kuang J H，Huang B W.The effect of blade crack on mode localization in rotating bladed disks［J］.Journal of Sound and Vibration，1999，227（1）：85－103.

［15］葛永庆，安连锁.裂纹参数对叶片固有频率影响的研究［J］.动力工程，2008，28（4）：519－522.GE Yongqing，AN Liansuo.Study of the influence of crack parameters on the blade natural frequencies［J］.Journal of Power Engineering，2008，28（4）：519－522.

［16］Wu G Y，Shih Y S.Dynamic instability of rectangular plate with an edge crack［J］.Computers＆ Structures，2005，84（1／2）：1－10.

［17］傅志方.模态分析理论与应用［M］.上海：上海交通大学出版社，2000.