随机海浪过程模拟的随机函数方法

刘章军，刘 玲

（三峡大学 土木与建筑学院，湖北 宜昌 443002）

海浪理论可分两类［1］：一类为水波理论（规则波理论），特点为将海浪运动视为确定的函数形式，利用流体力学方法研究海浪动力学性质及运动规律；另一类为随机海浪理论（不规则波理论），特点为将海浪运动视为随机过程，利用随机过程理论研究海浪运动的统计特征及分布规律。我国随机海浪理论研究始于20世纪80年代初［2］，在海浪谱、海浪特征量统计分布、随机波群及深水海浪破碎统计特征等方面取得诸多研究成果，已广泛用于海浪预报、船舶设计、海洋工程及海岸工程设计［3］。随机波浪作用作为海洋工程、海岸工程及船舶的主要动力荷载，如何合理描述、模拟随机波浪作用是海浪理论研究的重要课题。为此，文献［4］对工程设计中的海洋波浪进行模拟；文献［5－6］利用快速Hartley变换对随机海浪过程模拟、分析；文献［7］利用已有的各种方法对不规则海浪进行数值模拟与频谱分析；文献［8］利用能量等分法及有理谱法分别建立随机海浪模型并仿真分析；文献［9］利用本征正交分解方法对多变量随机海浪场进行数值模拟分析；文献［10］在方向谱基础上用谱表示方法模拟三维随机海浪过程。这些模拟方法主要以海浪谱或方向谱为基础，需通过上千个随机变量的模拟方能获得所需精度。由于无法从样本函数集合的角度研究随机海浪过程，极大增加了海洋结构随机动力反应分析难度。

采用随机函数思想研究工程随机激励（过程）为较新途径。文献［11］建立基于随机Fourier函数的物理海浪谱模型，首次从基本随机变量集合的角度研究海浪谱；文献［12］提出随机过程的随机谐和函数表达；文献［13］对谱表示方法的频率选点进行优化，以实现用少量若干基本随机变量描述随机过程的目的；文献［14］提出随机过程模拟的谱表示－随机函数方法；文献［15］提出正交展开－随机函数模拟方法，并应用于地震动过程及脉动风速过程。本文在文献［14－15］基础上进一步模拟随机海浪过程，并进行谱表示－随机函数与正交展开－随机函数两种模拟方法优缺点的对比分析，获得有益结果，可为工程应用提供合理的模拟方法。

1 平稳随机过程模拟的谱表示

对任意一维、单变量、零均值、双边功率谱密度函数Sf0（ω）的实平稳随机过程 f0（t），当功率谱密度函数满足 Sf0（ω0）＝Sf0（0）＝0条件时，模拟的第一类谱表示［14］为

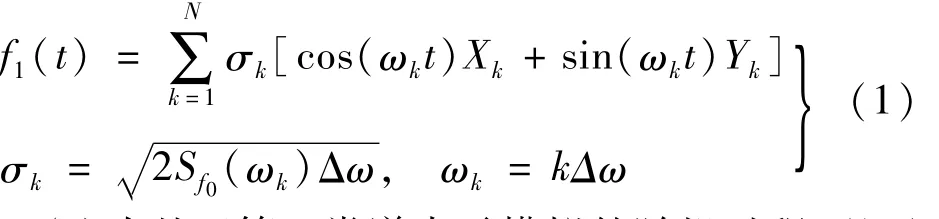
式中：f1（t）为基于第一类谱表示模拟的随机过程，以区别于原随机过程 f0（t）；｛Xk，Yk｝（k＝1，2，…，N）为一组标准正交随机变量［14］，即

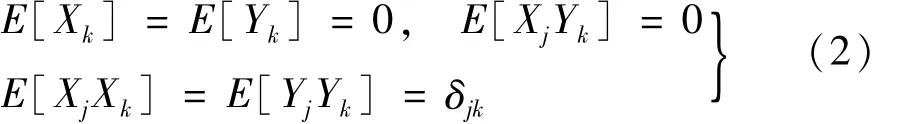
式中：E［·］为数学期望；δjk为 Kroneckerdelta符号。

基于第一类谱表示模拟的均方相对误差［14］为

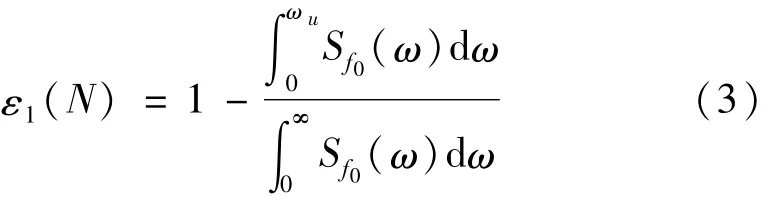
式中：ωu＝NΔω为截断频率，N为截断项数。基于谱表示模拟的均方相对误差 ε1（N）1，对随机海浪过程，本文建议 ε1（N）≤0.001。

2 平稳随机过程模拟的正交展开

设连续的实随机过程｛f0（t），0≤t≤T｝为零均值的二阶矩过程，其近似正交展开式［15］为

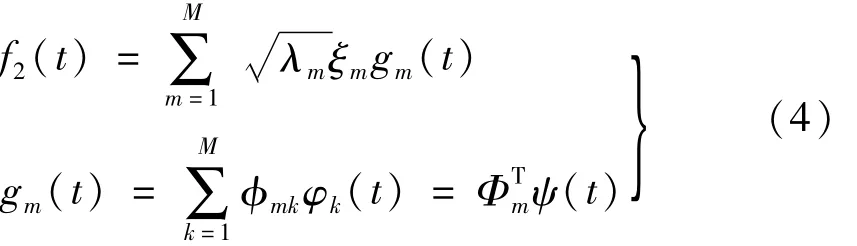
式中：f2（t）为基于正交展开模拟的随机过程，区别于原随机过程 f0（t）；M为展开项数；ψ（t）＝｛φ1（t），φ2（t），…，φM（t）｝T为区间［0，T］上标准三角函数基前 M个基函数组成的正交函数集；ξm（m＝1，2，…，M）为标准正交随机变量，即

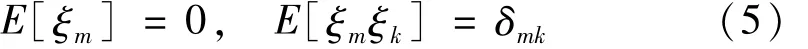
式（4）中 λm与 Φm＝｛m1，m2，…，mM｝T为相关矩阵R的第m个特征值与标准特征向量，即

式中：R＝［rij］M×M为相关矩阵，其元素计算式［15］为

对零均值的实平稳随机过程 f0（t），有 Rf0（t1，t2）＝Rf0（t2－t1）＝Rf0（τ）。于是，基于正交展开模拟的均方相对误差［15］可表示为

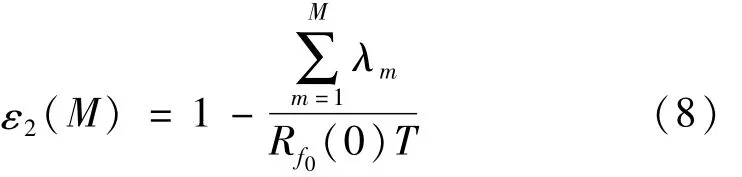
特征值λm与标准特征向量Φm应按特征值大小递减排列。通常基于正交展开模拟的均方相对误差ε2（M）1。对随机海浪过程，本文建议 ε2（M）≤0.01。

3 标准正交随机变量的随机函数表达

若直接用以上两种方法模拟随机海浪过程，往往需对数百上千个标准正交随机变量进行数值模拟，将极大增加海洋工程结构随机动力分析难度。为此采用随机函数思想［14－15］，将两种模拟方法中的标准正交随机变量表达为一个基本随机变量的函数形式。对平稳随机过程模拟的正交展开法，其标准正交随机变量的随机函数形式［6］为

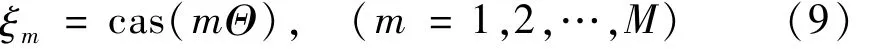
式中：cas（x）＝cos（x）＋sin（x）为 Hartley正交基函数；Θ为基本随机变量，在区间［－π，π］均匀分布。

易验证［15］式（9）构造的随机函数形式满足式（5）基本条件，其标准正交随机变量 ξm（m＝1，2，…，M）一般为非高斯分布。利用式（9）中标准正交随机变量的随机函数形式，即可构造一组高斯标准正交（独立）随机变量［15］，即

式中：Θ为基本随机变量，在区间［－π，π］均匀分布。

易验证式（11）构造的标准正交随机变量Xn，Yn满足基本条件式（2）。同样，由式（11）构造的标准正交随机变量为非高斯。利用式（11）标准正交随机变量的随机函数形式，即可构造二组高斯标准正交（独立）随机变量［14］，即

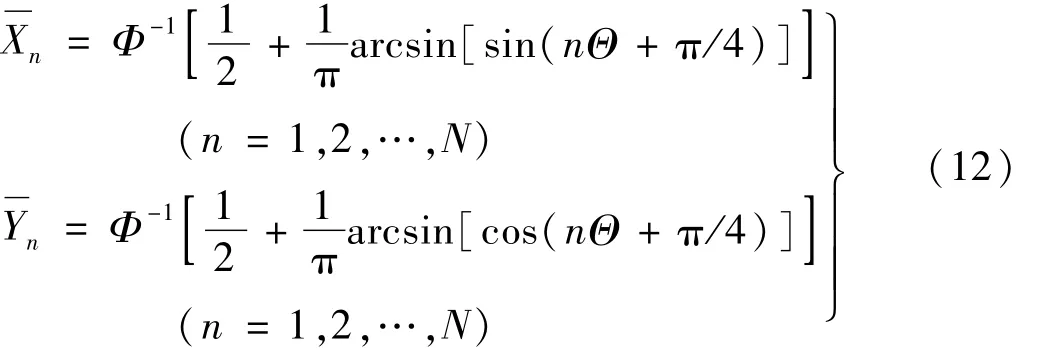
获得非高斯或高斯标准正交随机变量｛n，n｝（n＝1，2，…，N）后，利用 Matlab程序自带的 rand（＇state＇，0）、randperm（N）将｛n｝一一映射到｛Xk，Yk｝，即n→Xkn→Yk。因此式（1）所需标准正交随机变量｛Xk，Yk｝（k＝1，2，…，N）即被唯一确定。

在随机过程模拟的正交展开式（4）中，其标准正交随机变量 ξm（m＝1，2，…，M）直接按式（9）或式（10）的随机函数形式产生。而在随机过程模拟的第一类谱表示中，按式（11）或式（12）生成的标准正交随机变量nn｝（n＝1，2，…，N）需经某种映射才能成为式（1）所需的标准正交随机变量｛Xk，Yk｝（k＝1，2，…，N）。原因可能为在随机过程模拟的正交展开式（4）中，展开级数项按特征值（即携带的能量）大小递减排列，标准正交随机变量的随机函数表达形式亦从低阶到高阶（即从主到次）依次排列，两者排列次序一致。在随机过程模拟的谱表示式（1）中，展开级数项则按功率谱密度函数所在频率区间内能量排列，所携带的能量大小与功率谱密度函数分布有关，与标准正交随机变量的随机函数表达形式排列次序不一致，因而需对随机函数形式生成的标准正交随机变量经某种排序后才能成为谱表示式（1）中所需的标准正交随机变量。

4 随机海浪过程模拟

在随机海浪理论中通常将海浪视为平稳随机过程。为应用谱表示－随机函数与正交展开－随机函数两种方法模拟随机海浪过程，以经典PiersonMoscowitz谱（P－M谱）为目标谱，其单边功率谱密度函数表达式［2］为

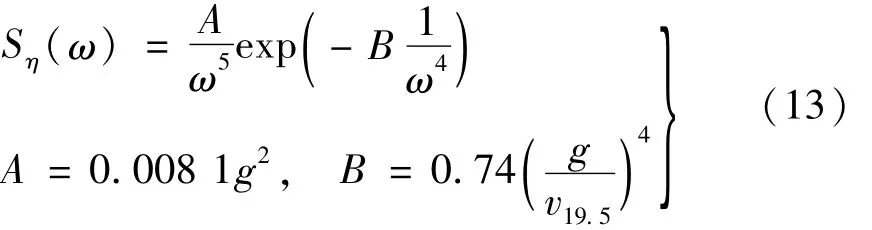
式中：Sη（ω）为海浪过程η（t）的单边功率谱密度函数（m2·s）；g＝9.81 m／s2为重力加速度；v19.5为海面19.5 m高处风速（m／s）。

对零均值的平稳随机过程η（t），据目标功率谱的表达式（13）知目标标准差表达式为

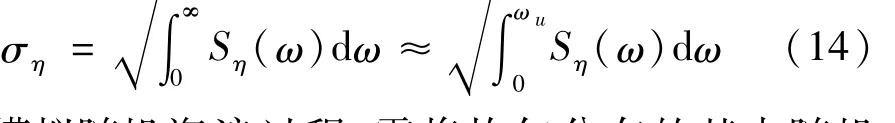
为模拟随机海浪过程，需将均匀分布的基本随机变量Θ在区间［－π，π］离散化，本文建议离散代表点计算式为

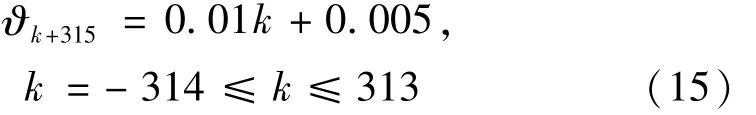
式中：k为整数。

可构成离散代表点集｛1，2，…，628｝，s＝628为离散点数，同时计算离散代表点的赋得概率Pi（i＝1，2，…，s），显然 Pi＝1。将每个离散代表点i（i＝1，2，…，s）代入相应标准正交随机变量的随机函数表达式，即可获得一组标准正交随机变量的离散点值，再将该组离散点值代入对应的随机过程模拟式中，即可产生随机过程的一个样本函数，从而构成随机过程的样本函数集合，而每条样本函数的出现概率即为离散代表点的赋值概率。以式（9）为例，对任意给定的离散代表点i，一组标准正交随机变量的离散点值为＝cas（mi），（m＝1，2，…，M）；再将标准正交随机变量的离散点值（m＝1，2，…，M）代入随机过程模拟的正交展开式（4），即可生成随机过程一条样本函数，该样本函数的出现概率即为Pi。

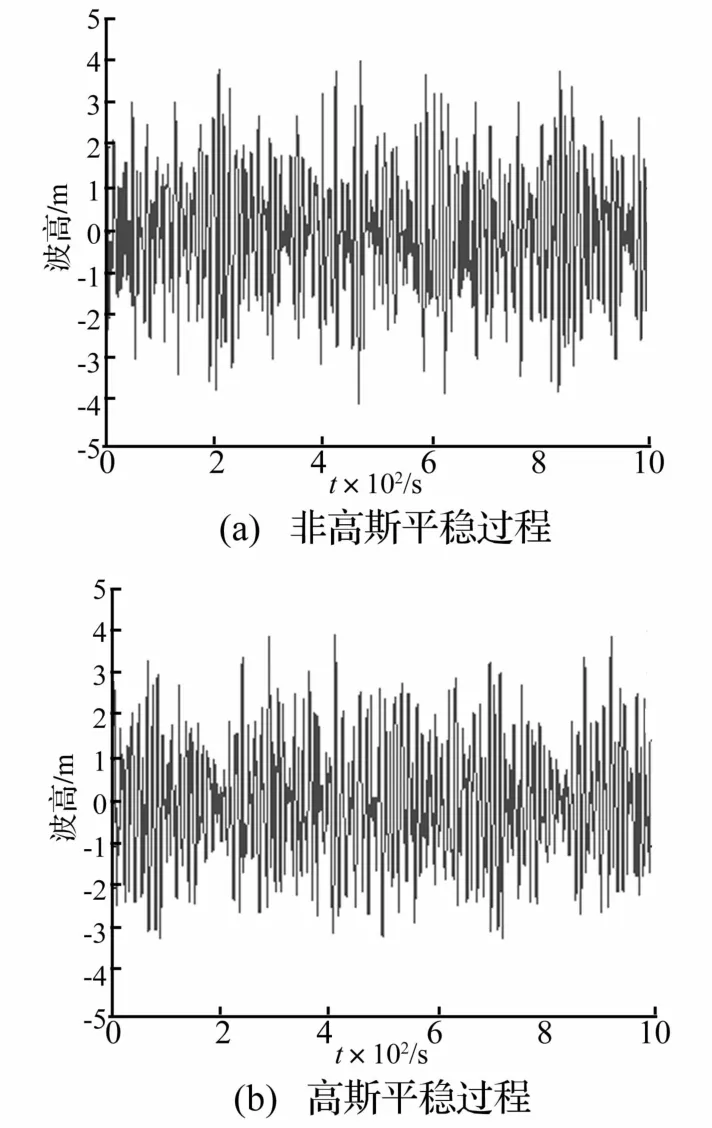
图1 海浪过程的样本函数Fig.1 Time histories of generated wave using spectral representation and random functions

4.1 谱表示－随机函数模拟

在平稳随机过程模拟的第一类谱表示中，截断频率 ωu＝10 rad／s，Δω＝0.01 rad／s，N＝1 000；均方相对误差 ε1（N）＝0.000 01，满足 ε1（N）≤0.001条件。海浪谱参数 v19.5＝16.24 m／s，海浪持续时间 T＝1 000 s，时间步长 Δt＝0.1 s，满足 Δt≤π／ωu条件。非高斯、高斯随机海浪过程的样本时程曲线见图1。

为对平稳随机过程的二阶数值统计特征进行比较，在式（11）或式（12）基础上用平稳随机过程模拟的谱表示式（1）生成628条海浪过程的样本函数集合。目标均值为零、标准差为1.406 4 m。限于篇幅，图2仅给出非高斯海浪过程二阶数值统计特征与目标值比较。其中图2（a）为628条样本函数的总体均值、标准差与目标均值、标准差比较；图2（b）为628条样本函数的总体功率谱与目标功率谱比较。可见其符合程度均十分理想。

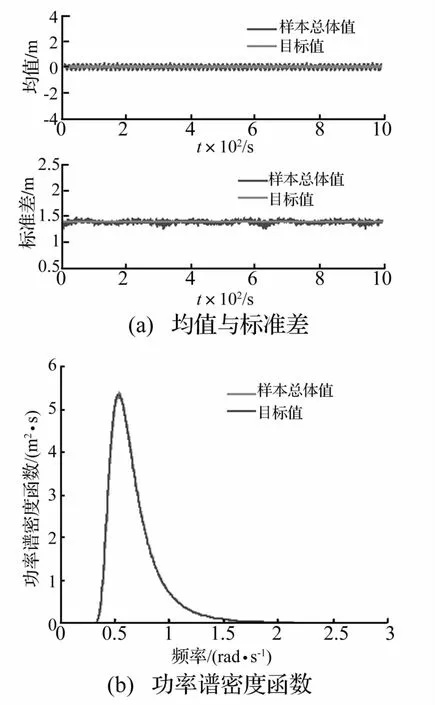
图2 628条非高斯海浪过程样本函数统计特征与目标值比较Fig.2 Comparison the targets and secondorder statistics of 628 generated NonGaussian process’s samples using spectral representation and random functions

4.2 正交展开－随机函数模拟

在平稳随机过程模拟的正交展开方法中需计算相关矩阵R的特征值λm与标准特征向量Φm。而R则由平稳随机过程的自相关函数计算。因此，需据海浪过程功率谱密度函数求出自相关函数。由于通过目标功率谱（式（13））的傅里叶逆变换计算自相关函数较困难，尤其获取解析解答。为此，本文利用有理谱［8］逼近海浪过程的目标功率谱。

利用有理谱定义海浪过程等价功率谱（单边谱）为

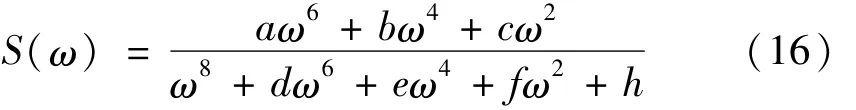
式中：S（ω）为海浪过程的等价功率谱；a，b，c，d，e，f，h为待定参数。

据参数估计理论，有

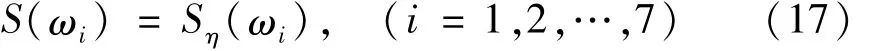
式中：Sη（ω）为海浪过程目标功率谱（式（13））。

本文据 ωi＝0.25 rad／s，0.4 rad／s，0.5 rad／s，0.6 rad／s，0.8 rad／s，1.0 rad／s，1.2 rad／s即可求出 a＝－0.001 9，b＝0.379 9，c＝－0.023 7，d＝－0.918 3，e＝0.550 0，f＝－0.146 2，h＝0.016 1，此处已略去各参数单位。

将等价功率谱改写为

海浪过程的等价功率谱与目标功率谱比较见图3。由图3看出，除局部略有偏差外两者符合程度较好，能满足精度要求。

据自相关函数表达式（19）、（20）并利用式（7）计算相关矩阵R，海浪持续时间T＝1 000 s，时间延滞τ＝t2－t1，展开项数 M＝600，均方相对误差 ε2（M）＝0.008，满足 ε2（M）≤0.01条件。获得 R后即可计算特征值λm与标准特征向量Φm。

据正交展开式（4）可生成628条具有给定赋值概率 Pi（i＝1，2，…，s）的海浪过程样本函数集合，海浪过程样本持续时间T＝1 000 s，时间步长 Δt＝0.1 s。用正交展开－随机函数方法生成的样本时程曲线见图4。高斯海浪过程二阶数值统计特征与目标值比较见图5。图5（a）为样本总体均值、标准差与目标均值、标准差比较；图5（b）为样本总体功率谱与目标功率谱比较。可见其符合程度十分理想。

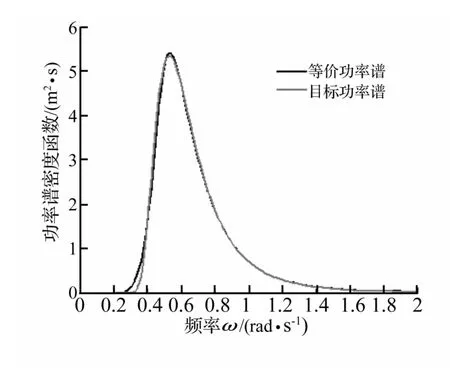
图3 等价功率谱与目标谱比较Fig.3 Comparison the target spectrum and its equivalent power spectrum

图4 海浪过程样本函数Fig.4 Time histories of generated wave using orthogonal expansion and random functions

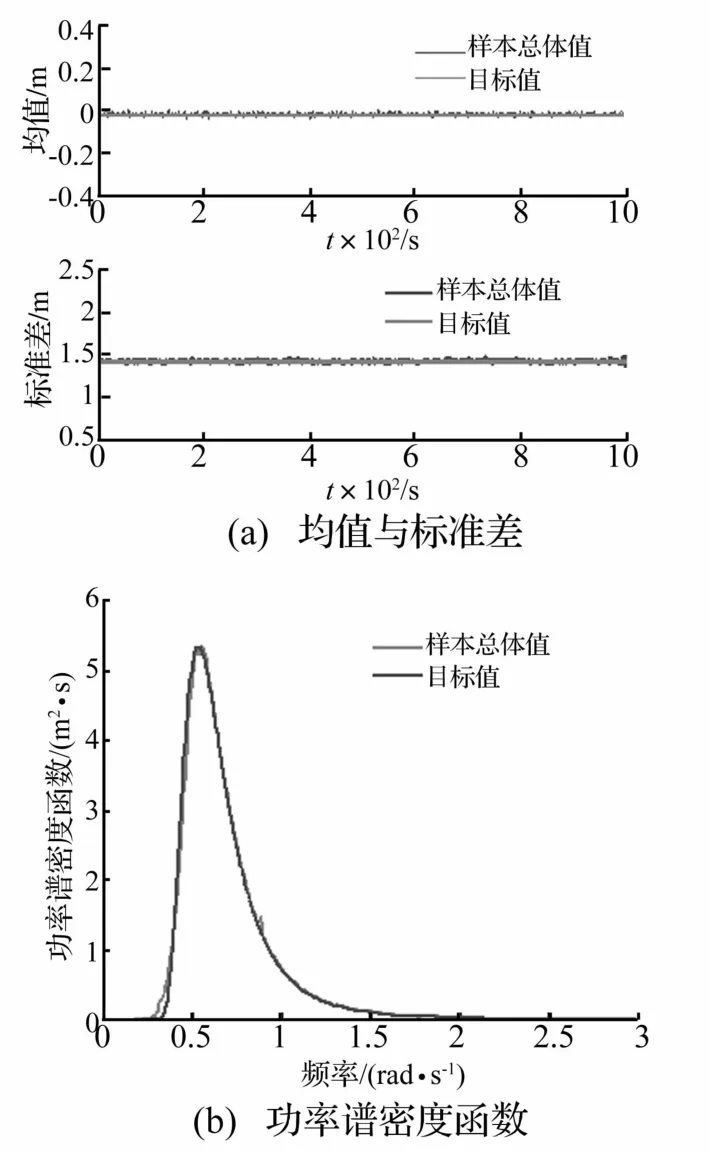
图5 628条高斯海浪过程样本函数的统计特征与目标值比较Fig.5 Comparison the targets and secondorder statistics of 628 generated Gaussian process’s samplesusing orthogonal expansion and random functions

5 两种模拟方法比较

通过两种方法对随机海浪过程模拟，可将平稳随机过程模拟的谱表示－随机函数与正交展开－随机函数方法比较如下：

（1）两种模拟方法均能较好再现平稳随机过程的样本函数及从样本函数集合角度研究随机过程，在二阶数值统计特征上两种方法的模拟效果均较理想。

（2）谱表示－随机函数方法以功率谱密度函数为基础模拟，与工程中大多以功率谱作为随机激励模型一致；而正交展开－随机函数方法以自相关函数或自协方差函数为基础模拟，需计算相关矩阵及特征值与标准特征向量，计算量较大。

（3）在均方相对误差上谱表示－随机函数方法较易实施及控制，仅需控制频率间隔Δω及级数项数N；而正交展开－随机函数方法则较难实施及控制，尤其达到一定精度后哪怕再稍提高精度则需较大计算量。

（4）谱表示－随机函数方法对模拟过程的持续时间可任意选择，即可据所需随时调整；而正交展开－随机函数方法则需事先确定，一旦确定后不能再调整。

（5）随机过程模拟的正交展开－随机函数方法中，标准正交随机变量直接按随机函数表达式产生；而谱表示－随机函数方法中标准正交随机变量不能直接由随机函数表达式产生，需经某种映射后才能成为谱表示中所需标准正交随机变量。

以上两种模拟方法各有优缺点，工程实际中可据所需适当选择。

6 结 论

在平稳随机过程模拟的谱表示与正交展开两种经典方法中，通过引入标准正交随机变量的随机函数表达式，均能实现用一个基本随机变量模拟原随机过程目的。通过选择基本随机变量的离散代表点集，即可获得随机过程的样本函数集合，实现从样本函数集合角度研究随机动力激励，可大幅降低随机动力学分析难度。用谱表示－随机函数与正交展开－随机函数两种方法对随机海浪过程进行模拟分析，均获得较理想结果，但从工程应用角度谱表示－随机函数方法更易实施，且易推广到以方向谱为基础的随机海浪模拟，亦为三维随机海浪模拟提供合理方法。

［1］钱荣.大直径圆柱壳结构动力响应及随机波浪力数值模拟研究［D］.天津：天津大学，2004.

［2］文圣常，余宙文.海浪理论与计算原理［M］.北京：科学出版社，1984.

［3］俞聿修.随机波浪及其工程应用（第三版）［M］.大连：大连理工大学出版社，2003.

［4］Borgman L E.Ocean wave simulation for engineering design［J］.Journal of the Waterways and Harbors Division，ASCE，1969，95（4）：557－583.

［5］Winterstein S R.Random process simulation with the fast Hartley transform［J］.Journal of Sound and Vibration，1990，137（3）：527－531.

［6］Germán R.Analysis and simulation of wave records through fast Hartley transform［J］. Ocean Engineering，2003，30（17）：2255－2273.

［7］Morooka CK，Yokoo I H.Numerical simulation and spectral analysis of irregular sea waves［J］.International Journal of Offshore and Polar Engineering，1997，7（3）：189－196.

［8］邱宏安.随机海浪模型的建立及仿真分析［J］.系统仿真学报，2000，12（3）：226－228.QIU Hongan.Establishing and simulation for random ocean state model［J］.Journal of System Simulation，2000，12（3）：226－228.

［9］Di Paola M，Pisano A A.Multivariate stochastic wave generation［J］.Applied Ocean Research，1996，18（6）：361－365.

［10］白连平，陈秀真.三维随机海浪的数值模拟［J］.海洋工程，2000，18（4）：32－35.BAI Lianping，CHEN Xiuzhen.Numerical simulation of threedimensional random wave［J］.Ocean Engineering，2000，18（4）：32－35.

［11］徐亚洲，李杰.基于拟层流风波生成机制的海浪谱模型［J］.海洋工程，2012，30（1）：83－91.XU Yazhou，LI Jie.An ocean wave spectrum model based on quasilaminar windinduced wave generation mechanism［J］.The Ocean Engineering，2012，30（1）：83－91.

［12］ Chen Jianbing，Sun Weiling，Li Jie，et al.Journal of Applied MechanicsTransactions of the ASME， 2013，80（1）：011001.

［13］Chen Jianbing，Li Jie.Optimal determination of frequencies in the spectral representation of stochastic processes［J］.Computational Mechanics，2013，51（5）：791－806.

［14］刘章军，方兴.平稳地震动过程的随机函数－谱表示模拟［J］.振动与冲击，2013，32（24）：6－10.LIU Zhangjun，FANG Xing.Simulation of stationary ground motion with random functions and spectral representation［J］.Journal of Vibration and Shock，2013，32（24）：6－10.

［15］刘章军，万勇，曾波.脉动风速过程模拟的正交展开－随机函数方法［J］.振动与冲击，2014，33（8）：120－124.LIU Zhangjun， WAN Yong， ZENG Bo. Simulation of fluctuating wind processes with an orthogonal expansionrandom function approach［J］.Journal of Vibration and Shock，2014，33（8）：120－124.