一种新的非高斯随机振动疲劳寿命估计方法
袁 毅,程军圣
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
结构振动疲劳是指结构所受动态交变载荷(振动、冲击、噪声载荷等)的频率分布与结构固有频率分布具有交集或相接近时,结构共振所导致的疲劳破坏现象[1-2]。振动疲劳现象普遍存在于航天、航空、交通运输等工程实际中,但由于其复杂性,相关研究依然不多[3]。
随机应力幅值概率密度函数模型的构造是振动疲劳寿命估计方法的关键,与雨流幅值概率密度越接近,模型精度就越高。到目前为止,频域疲劳寿命估计已经产生许多不同的方法,如 Dirlik,Tovo-Benasciutti和Zhao-Baker等。它们有一个共同特点,都只适用于平稳高斯随机过程。然而,在工程实际中结构承受的载荷经常受到外来随机激励的影响,使得真实载荷表现出一定的非高斯性。如果非高斯特性比较明显,将会对结构产生巨大的损伤,不容忽视[4]。因此,有必要研究非高斯随机过程下振动疲劳寿命估计。
目前,国内外解决非高斯随机过程下的振动疲劳寿命估计问题的方法较少,国外一般利用非高斯载荷的峭度因子进行经验修正,误差较大[5]。按照解决高斯随机过程下振动疲劳寿命估计的思路,解决非高斯问题也需要一个相应的随机应力幅值概率密度函数模型。蒋培等[6]提出利用非高斯概率密度函数的Hermite多项式渐近展开,利用其三维联合高阶统计特征,得到非高斯随机过程下的概率密度函数。该法适用于窄带、宽带、高斯、非高斯随机载荷下的疲劳寿命估计问题,具有很强的适应性,缺点是计算复杂。因此,本文提出采用高斯近似的方法来解决非高斯随机过程下的振动疲劳寿命估计问题。
高斯近似法采用Winterstein传递函数将非高斯随机过程转换成高斯随机过程,并通过非高斯修正系数建立非高斯随机过程下的疲劳损伤与高斯随机过程下的疲劳损伤之间的关系。这样就可以通过估算高斯随机过程下的疲劳损伤得到非高斯过程下的疲劳损伤。
基于高斯近似的非高斯随机过程振动疲劳寿命方法的关键是对非高斯修正系数模型的构造。本文首先证明了非高斯修正系数只与非高斯随机应力和经Win-terstein传递函数转换的高斯随机应力的谱矩有关。然后采用响应面法[7]构造一个关于应力谱矩和非高斯修正系数的多项式响应面模型。最后,利用高斯近似法估算非高斯随机振动疲劳损伤量,并与经过雨流计数和Miner损伤准则估算的非高斯随机过程下疲劳损伤对比,结果表明:高斯近似法具有较好的精度。
1 传递函数法
对一个给定的高斯随机过程X(t),引进一个非线性传递函数 G(·),可以使得满足 Z(t)=G(X(t))的随机过程Z(t)为具有指定偏斜度和峭度的非高斯随机过程。而且,逆传递函数g(·)=G-1(·)可以用来将具有指定偏斜度和峭度的非高斯随机过程转化成高斯随机过程,满足 X(t)=g(Z(t))。目前,对满足 Z(t)=G(X(t))的传递函数G(·)的定义主要有Ochi提出的单调指数函数模型和Winterstein等[8]提出的单调的三次Hermite多项式模型。其中,Winterstein等提出的单调三次Hermite多项式模型在非线性问题中具有较高的精度被普遍采用。
通常用三阶统计量偏斜度γ3和四阶统计量峭度γ4来描述非高斯信号:

当峭度值γ4>3时,非高斯随机过程Z(t)的Win-terstein的传递函数G(·)定义为:
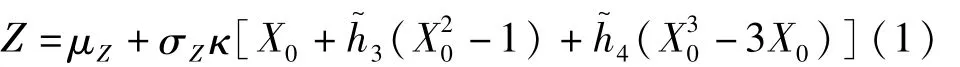
其中,X0为标准正态随机过程,X0=(X-μX)/σX;h~3和h~4是与非高斯随机过程偏斜度γ3和峭度γ4相关联的系数;系数κ保证非高斯随机过程和高斯随机过程具有相同的均方根值。
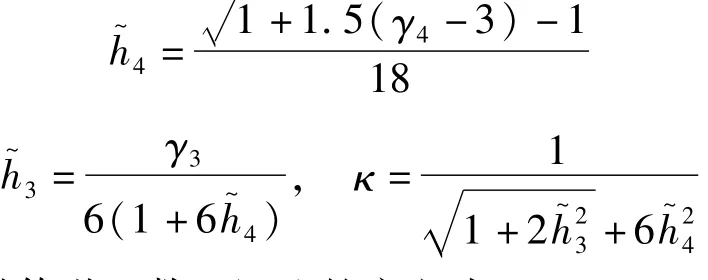
对逆传递函数g(·)的定义为:
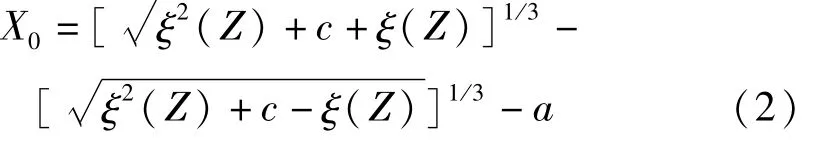

当峭度值 γ4<3,非高斯随机过程 Z(t)的 Winter-stein的逆数g(·)定义为:
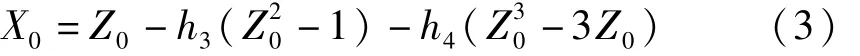
其中,Z0=(Z-μZ)/σZ,h3=γ3/6,h4=(γ4-3)/24。
2 基于高斯近似法的非高斯疲劳寿命估计
高斯近似法:采用Winterstein传递函数将非高斯随机过程转换成高斯随机过程,并通过非高斯修正系数建立非高斯随机过程下的疲劳损伤与高斯随机过程下的疲劳损伤之间的关系。如式(4)所示:

其中,表示非高斯随机过程下结构的振动疲劳损伤;表示经Winterstein传递函数转换的高斯随机过程下的振动疲劳损伤;λ表示非高斯修正系数。
这样就可以通过估算高斯随机过程下的疲劳损伤得到非高斯过程下的疲劳损伤。
目前,对于高斯随机过程下的振动疲劳研究已经比较成熟,研究非高斯随机过程下的振动疲劳的关键就是非高斯修正系数的模型。下面将首先讨论,非高斯修正系数由哪些参数决定。
2.1 非高斯修正系数
一般宽带随机过程的雨流幅值分布模型可以假设由n个双参数Weibull分布表示[9]
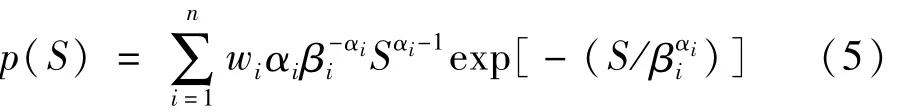
其中,wi为权重系数,且αi和 βi分别为Weibull分布的形状参数和尺度参数。并且各参数都是关于应力功率谱的零阶、一阶、二阶和四阶谱矩等四个参数的函数。任意阶谱矩定义为[10]:
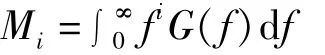
其中,f表示频率;G(f)表示单边功率谱密度。
总疲劳失效可以表示为:
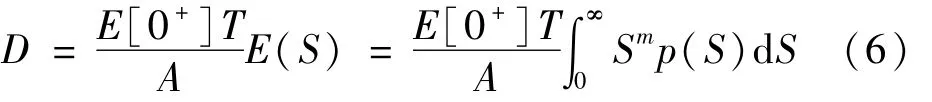
其中,E[0+]表示应力幅值正穿越0值频率;A和m为材料参数,T代表总时间。
联立式(5)和式(6)得到:
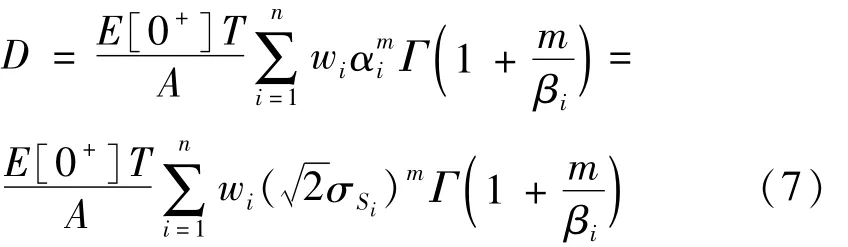
其中,σS表示应力幅值均方根值和Γ表示伽马函数。
因此,非高斯修正系数可以表示为:
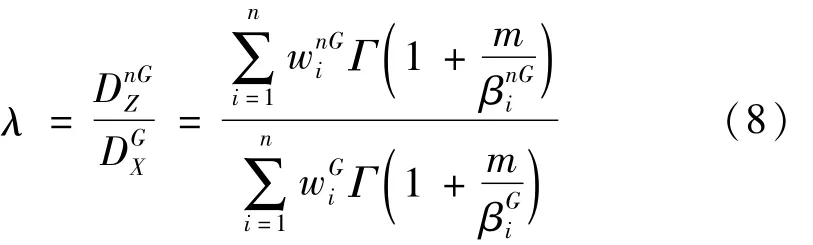
从上式可以看出,非高斯修正系数λ只与高斯随机过程下的谱矩:M′0、M′1、M′2、M′4,非高斯随机过程下的谱矩 M0、M1、M2、M4,以及材料参数 S-N曲线中双对数斜率m有关。因此,针对某一特定材料的非高斯修正系数将只与8个谱矩有关。又由于Winterstein传递函数模型保证了转换前后零阶谱矩相等,所以非高斯修正系数将只与7个谱矩参数有关。因此,可以构建非高斯修正系数与7个谱矩之间关系的模型。
2.2 非高斯修正系数的多项式响应面模型
响应面法是一种结合实验设计与统计理论的优化设计方法。响应面法的关键是用简单的表达式逼近复杂的隐式函数,反映输入变量和响应的映射关系。目前,主要的响应面模型有:多项式响应面法和神经网络响应面法。多项式响应面法运用不同阶次的多项式对样本进行拟合,构造目标响应与输入变量的近似表达式,表达式形势简单,模型计算量小,收敛速度快,是目前研究和应用比较广泛的一种响应面法[7]。因此可以构建一个关于非高斯修正系数和谱矩之间的多项式响应面模型。
为了满足一定的精度,同时为了使得模型不太复杂,选择构建非高斯修正系数与谱矩之间的多项式响应面模型为二阶多项式模型。具体表达式如式(9)所示:
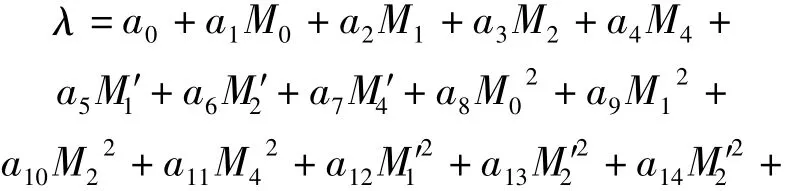

其中,ai(i=0,1,2…35)表示二次多项式响应面模型的系数。
下面将具体讨论非高斯修正系数的二次多项式响应面模型系数的确定。
首先,根据非高斯修正系数只与7个谱矩参数有关,确定采用二阶模型所需要的基函数个数:

然后,利用Winterstein传递函数模型将具有一定偏斜度和峭度的非高斯随机过程转换成高斯过程,并求出他们各自的谱矩,最后结合雨流计数与Miner准则求出单位时间非高斯随过程和高斯随机过程在材料参数A=1,m=3时的非高斯修正系数。需要的总样本数大约为60组,这里列举了10组样本,如表1所示。可以清楚的看到两点:第一,经Winterstein模型转换之后的高斯随机过程与原来的非高斯随机过程具有相同的一阶谱矩,与Winterstein模型保证转换前后均方根值不变这一结论相吻合;第二,强化系数都大于1,这符合非高斯随机过程对结构造成更大程度的损伤这一结论。此外,这里的非高斯修正系数普遍偏小的一个重要原因是材料参数m=3偏小,如果m=10,强化系数可以达到100~200,甚至更大,这与文献[3]中提到的非高斯修正系数为295比较吻合。
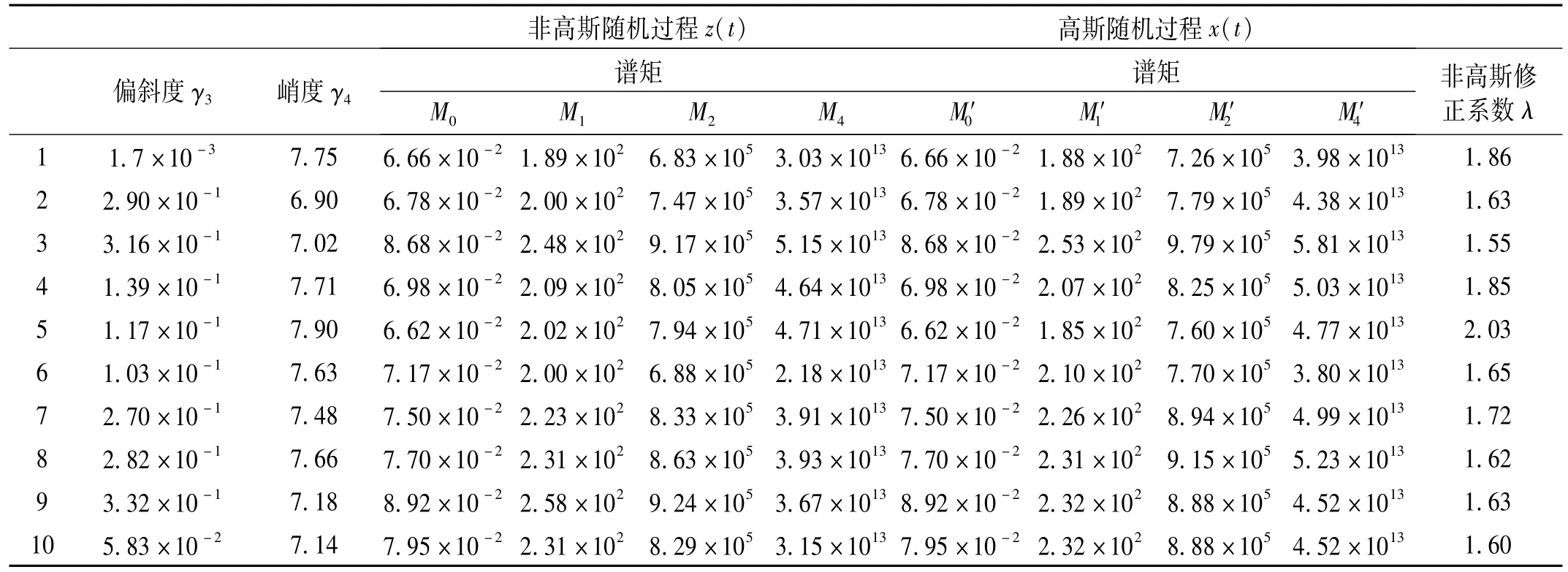
表1 10组非高斯随机过程样本及经W interstein模型转换后高斯随机过程对比Tab.1 A 10 samples comparison of non-Gaussian random process and the Gaussian random process after converted byW interstein model

表2 非高斯修正系数的多项式响应面模型系数Tab.2 The polynom ial response surfacemodel coefficient of the non-Gaussian correction coefficient
从表1中可以清楚的看到非高斯随机过程和高斯随机过程的零阶谱矩是相等的,这与Winterstein模型很符合。
最后,通过最小二乘拟合求得非高斯修正系数的多项式响应面法模型系数如表2所示。
2.3 高斯近似法在非高斯振动疲劳寿命估计中的应用
首先,构造1 000组具有不同偏斜度和峭度值的非高斯随机应力信号,计算出非高斯随机应力的4阶谱矩,并采用雨流计数和Miner损伤准则得到非高斯随机应力下的单位损伤量。
然后,利用 Winterstein模型中传递函数将上述1 000组非高斯随机应力信号近似成1 000组高斯随机信号,计算出高斯随机应力的4阶谱矩,并再次采用雨流计数和Miner损伤准则得到高斯随机应力下的单位损伤量。
然后,用本文构建的多项式响应面模型,计算出1 000组非高斯随机信号的非高斯应力修正系数。
然后,利用高斯随机应力下的单位损伤量和非高斯应力修正系数得到经非高斯修正后的非高斯随机应力下的单位损伤量。
最后,对两次得到的非高斯随机应力下的单位损伤量进行误差分析。结果如图1。
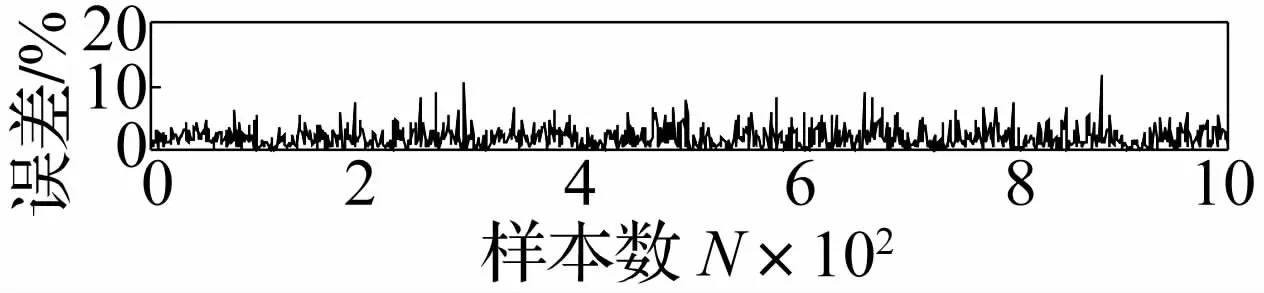
图1 1 000组不同非高斯随机应力信号的误差分析Fig.1 Error analysis of 1 000 samples for non-gaussian random signal
从上图可以看出,1000组样本中,除了个别样本的误差大于10%,大部分的样本信号都具有很好的效果。因此,本文提出的非高斯修正法对解决非高斯随机振动疲劳问题具有较好的效果。
3 结 论
(1)本文提出的采用高斯近似的非高斯随机过程下振动疲劳寿命估计方法具有较好的精度,为非高斯随机过程下振动疲劳问题提出了一种新的解决思路;
(2)高斯近似法的精度取决于非高斯修正系数模型的精度,因此,样本的选择必须选择合理的试验方案,并且获得尽可能多的样本;
(3)S-N曲线的双对数斜率m对非高斯修正系数影响较大,由于本文选择的m=3只是作为参考,得到的非高斯修正系数都偏小,实际中当m取到10左右时,非高斯修正系数可以达到100~200,甚至更大。
[1]高清振,王耀华,张晓南.基于样本法的某型飞机救生机构振动疲劳寿命估算[J].中国机械工程,2011,22(2):162-165.GAO Qing-zhen, WANG Yao-hua,ZHANG Xiao-nan.Fatigue life prediction of aeronautic rescue mechanism under random vibration based on sample approach[J].China Mechanical Engineering,2011,22(2):162-165.
[2]王明珠,姚卫星.双峰应力谱密度雨流幅值分布[J].航空学报,2009,30(9):1666-1671.WANG Ming-zhu, YAO Wei-xing. Rainflow amplitude distribution of bi-modal stress power spectral density[J].Acta Aeronautica et Astronautica Sinica,2009,30(9):1666-1671.
[3]姚起杭,姚军.工程结构的振动疲劳问题[J].应用力学学报,2006,23(1):12-15.YAO Qi-hang,YAO Jun.Vibration fatigue in engineering structures[J].Chinese Journal of Applied Mechanics,2006,23(1):12-15.
[4]王得志,蒋瑜,陈循,等.基于MSC的非高斯随机振动疲劳仿真研究[J].武汉理工大学学报,2010,32(9):52-55.WANG De-zhi,JIANG Yu,CHEN Xun,et al.Research on MSC-based fatigue simulation under non-Gaussian random vibration[J].Journal of Wuhan University of Technology,2010,32(9):52-55.
[5]Jimmy M H.Life prediction and damage acceleration based on the power spectral density of random vibration[J].Journal of the IES,1995,38(1):34-40.
[6]蒋培,温熙森,陈循,等.非高斯随机应力载荷频域疲劳寿命估计方法[J].机械工程学报,2006,42(2):51-56.JIANG Pei,WEN Xi-sen,CHEN Xun,et al.Spectral fatigue life estimate under non-Gaussian random stress[J].Chinese Journal of Mechanical Engineering,2006,42(2):51-56.
[7]聂祚兴.车身噪声传递函数的全局灵敏度分析及稳健优化设计[D].长沙:湖南大学,2012.
[8]Benasciutti D,Tovo R.Cycle distribution and fatigue damage assessment in broad-band non-Gaussian random Process[J].Probabilistic Engineering Mechanics,2005,20(2):115-127.
[9]王明珠.结构振动疲劳寿命分析方法研究[D].南京:南京航空航天大学,2009.
[10]张积亭,周苏枫.飞机典型构件振动疲劳寿命分析[J].机械科学与技术,2002,s1:15-16.ZHANG Ji-ting,ZHOU Su-feng.Analysis of vibration fatigue life of typical aircraft components[J].Mechanical Science and Technology,2002,s1:15-16.

