频率调制经验模态分解在轴承故障诊断中的应用
张 超,袁彦霞
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
现代机械设备中,轴承是最常用也是最易损坏的零件[1]。由于其破坏形式极其复杂,且通过传感器提取出来的振动信号具有非平稳特征,反映状态信息的能量也很微弱,给故障诊断带来了困难。如何从非平稳的振动信号中提取出故障特征信息是轴承故障诊断的关键。
经验模态分解(Empirical Mode Decomposition,EMD)是一种新型的信号处理方法,非常适合于非线性、非平稳信号[2]。一个非平稳信号通过EMD分解,可以得到若干个平稳的本征模函数(Intrinsic Mode Function,IMF)。然而,在处理实际信号时容易产生模态混淆问题是 EMD方法的最大缺陷[3]。也就是说,EMD方法的频率解析度不高,容易将相邻的两个不同频率的信号混淆成一个信号,从而产生无法预期的错误信息[4]。对于非平稳的随机振动信号,Wu等[5]提出了总体平均经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD),通过多次在原始信号中加入互不相关的白噪声,再进行EMD分解,最终将分解结果进行多次平均来消除噪声,进而解决EMD方法中的模态混淆问题。近年来,许多学者对EEMD方法进行了研究[6-8],但该方法效率很低。尤其对于衰减信号,效率更加低下,以至于不实用[3]。
基于此,本文研究了基于频率调制经验模态分解(Frequency Modulated Empirical Mode Decomposition,FM-EMD)的轴承故障诊断方法。文中首先对仿真信号分别进行EMD分解与FM-EMD分解,证明了FM-EMD方法的有效性。最后对发生滚动体剥落的故障轴承振动信号采用FM-EMD方法进行分解,提取出了故障特征频率,准确地确定了故障类型,完成了轴承故障诊断。
1 FM-EMD方法原理[3]
给定实数信号x(t),可通过Hilbert变换求出它对应的解析信号 z(t):
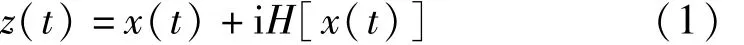
共轭信号 z*(t):
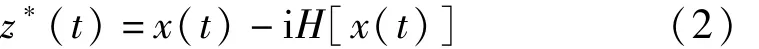
其中:
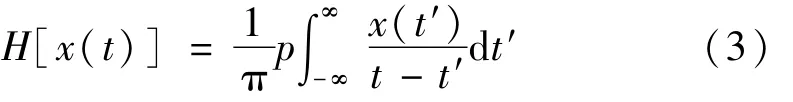
为希尔伯特变换;p为柯西数。
由解析函数的性质可知,z(t)的傅里叶变换只有正频率,而其共轭z*(t)的傅里叶变换则只有负频率。分别为函数 z(t)和 z*(t)定义调频函数 exp(-i2πfdt)和exp(-i2πfdt),这样就可得到已调函数 Z(t)和(t):
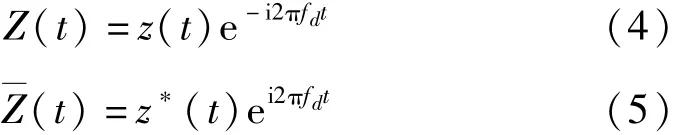
它们的傅里叶变换既包括正频率也包括负频率。
信号Z(t)可按如下方式分解:
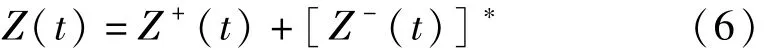
其中:
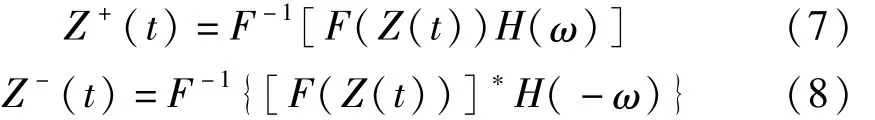
分别对应Z(t)的正频率成分和负频率成分;F为傅里叶变换算子;F-1傅里叶逆变换算子;H(ω)为理想滤波器:
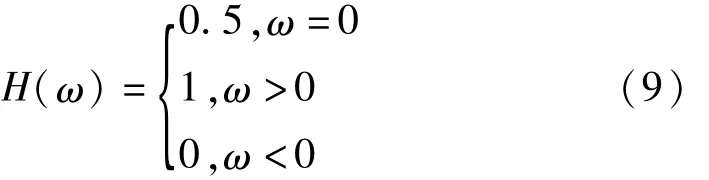
只需对Z+(t)和 Z-(t)的实数部分进行 EMD分解即可,这是因为:
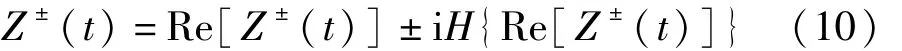
由EMD的原理可知,Z+(t)的实部可以分解成
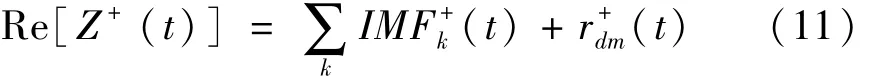
IM(t)是第k个IMF+为趋势线。
接着提取EMD分解结果中的主成分,并对其进行反向调频,调频函数为ei2πfdt。假设是Re[Z+(t)]的主成分,则还原后的原解析信号的的主要成分为
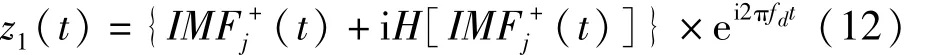
则可得到原信号x(t)的第一个IMF:
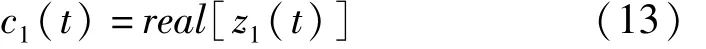
将 c1(t)从原信号 x(t)中分离出来,得到 x2(t),再把 x2(t)作为 x(t),重复以上过程,直到所有的 IMF,也就是xi(t)都得到提炼为止。
上述调频 EMD过程是针 Z(t)进行的,对于 Z—(t),可以用相同的方法进行处理。
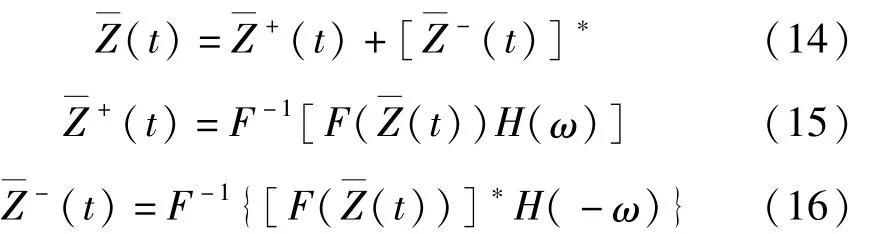
其中)和也均为解析信号。
对(t)的实数部分进行EMD分解,得到主成分IMF,经 Hilbert变换后,由 exp(-i2πfdt)解调,还原得到原始信号x(t)的IMF。
2 FM-EMD与EMD的数值仿真对比
已知仿真信号x(t)包含两个频率分量:f1=40 Hz,f2=30 Hz,采样频率 fs=1 000 Hz,数据长度 N=1 024,时域表达式为 x(t)=sin(2πf1t)+0.5sin(2πf2t),频率比f=f1/f2=0.75。时域波形和包络谱如图1所示。
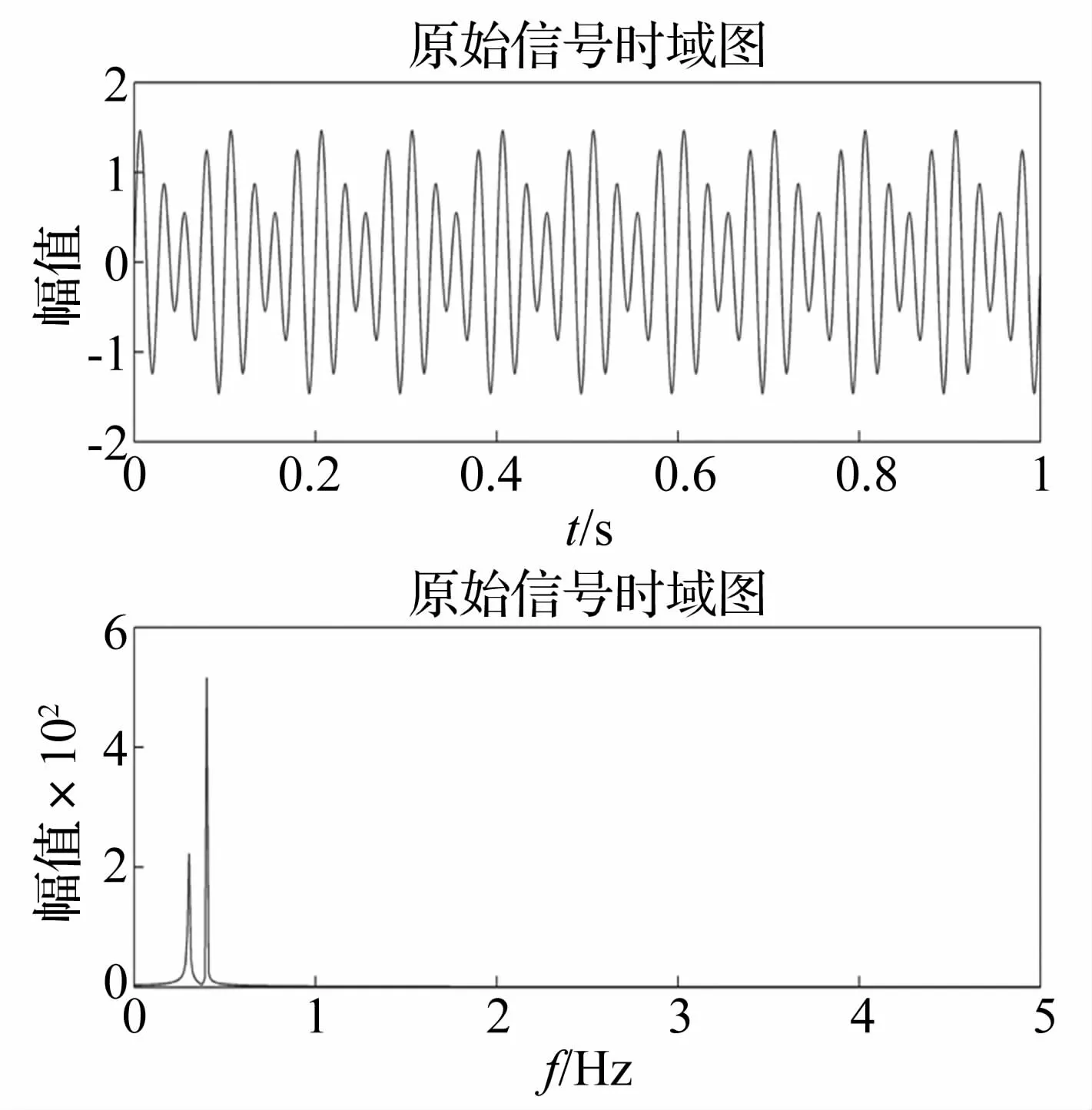
图1 仿真信号的时域波形和包络谱Fig.1 Figure oftime domain and envelope spectrum of simulation signal
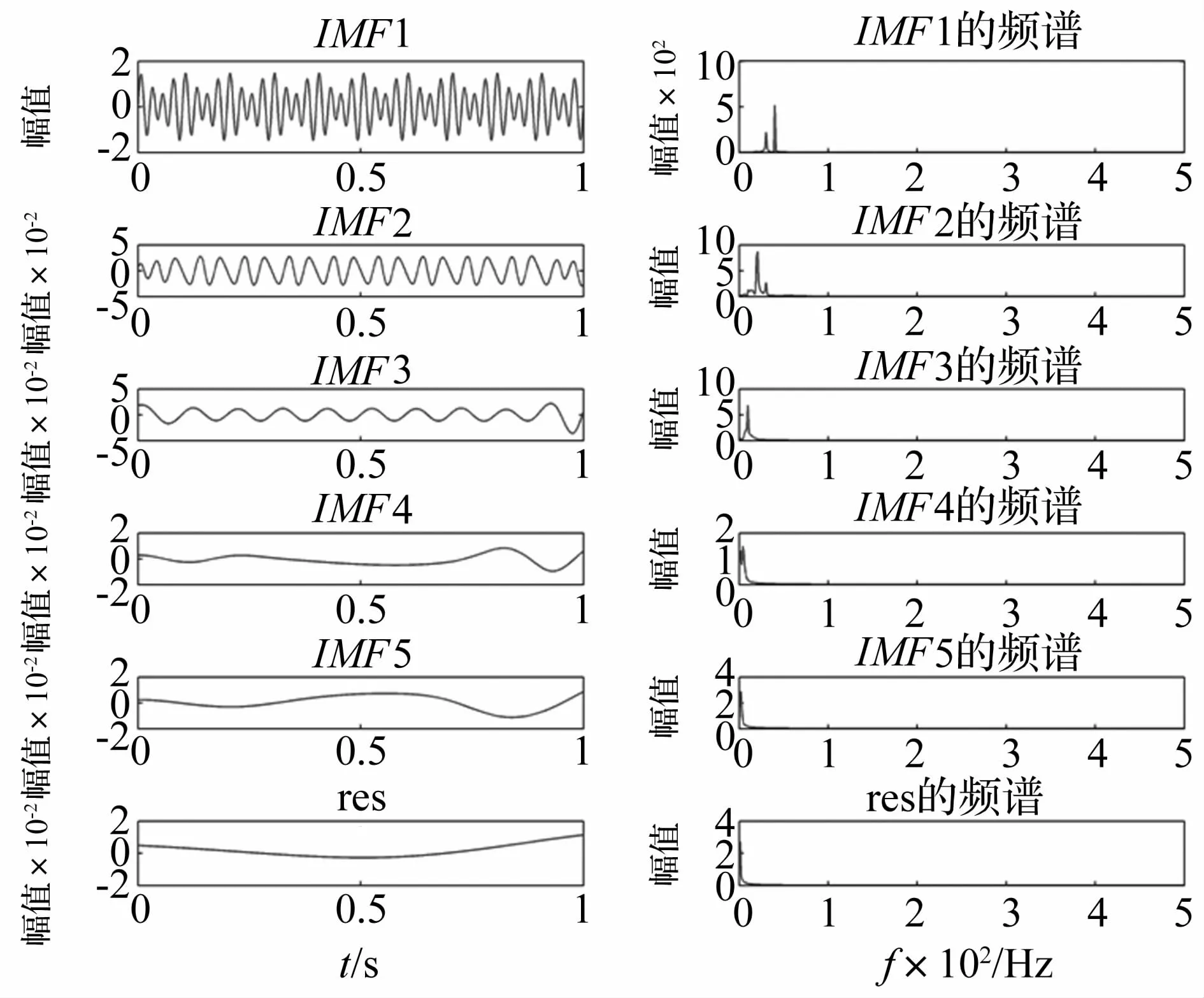
图2 仿真信号的EMD分解结果Fig.2 The EMD decomposition results of simulation signal
对该仿真信号进行EMD分解,分解结果如图2所示:
该仿真信号的频率比f=f1/f2=0.75,不在 EMD的工作空间内(只有在f<0.67或 af<1时,EMD方法才能有效识别总体信号中的个体成分[4])。由图2可以看出,信号x(t)被分解成五个IMF及余项,其中第一个IMF是原信号中分解出的时间尺度最短,频率最高的分量,代表信号中的高频成分,而且它的振幅大,说明其所占能量大,第五个IMF振幅很小。从IMF1的频谱图中更直观地显示出本征模函数分量IMF1中除含有频率为40 Hz的信号外,还明显含有频率为30 Hz的信号,说明本征模函数分量IMF1出现了明显的模态混叠现象。
调制频率fd具体数值的选取,可以通过原始信号的傅里叶变换初步估计,经反复试验后最终确定[3]。选用调频频率fd=25 Hz,利用调频EMD方法辨识高频IMF,分解得到原信号的第一个IMF分量c1,结果如图3所示。
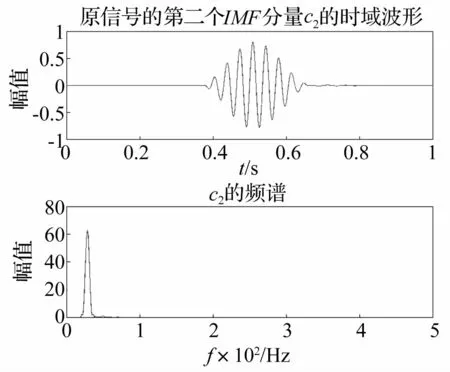
图4 IMF2的时域图及包络谱Fig.4 Time-domain diagram and envelope spectrum of IMF2
选用调频频率fd=20 Hz,利用调频EMD方法辨识低频IMF,分解得到原信号的第二个IMF分量c2,结果如图4所示。
图3和图4为仿真信号采用调频EMD方法分解得到的本征模函数,由图可见,得到两个与原信号分量相对应的IMF s,其中IMF1中模态混叠的现象有了显著的改善。IMF1中含有频率为40 Hz的信号,而频率为30 Hz的信号已经急剧缩减,很不明显。这就说明本征模函数分量IMF1的模态混叠现象已基本消除。因此,利用调频EMD方法后,成功地分解出了能代表原信号信息的2个IMF信号。
通过仿真信号的分解结果可以发现,如果信号的频率比较密集,超出EMD工作空间的范围,采用EMD方法对信号进行分解时,就会出现模态混叠现象。另外,如果信号的高频部分的幅值太小,EMD方法也不能正常工作。而调频EMD方法很好地解决了这个问题,得到能正确反映信号特征信息的IMF分量。
3 FM-EMD在轴承故障诊断中的应用
本文研究的是308轴承发生滚动体剥落故障时的振动加速度信号。其数据长度为8 192,数据的采样频率为20 kHz,滚动体个数z=8。图5为轴承故障信号的时域波形和包络谱。
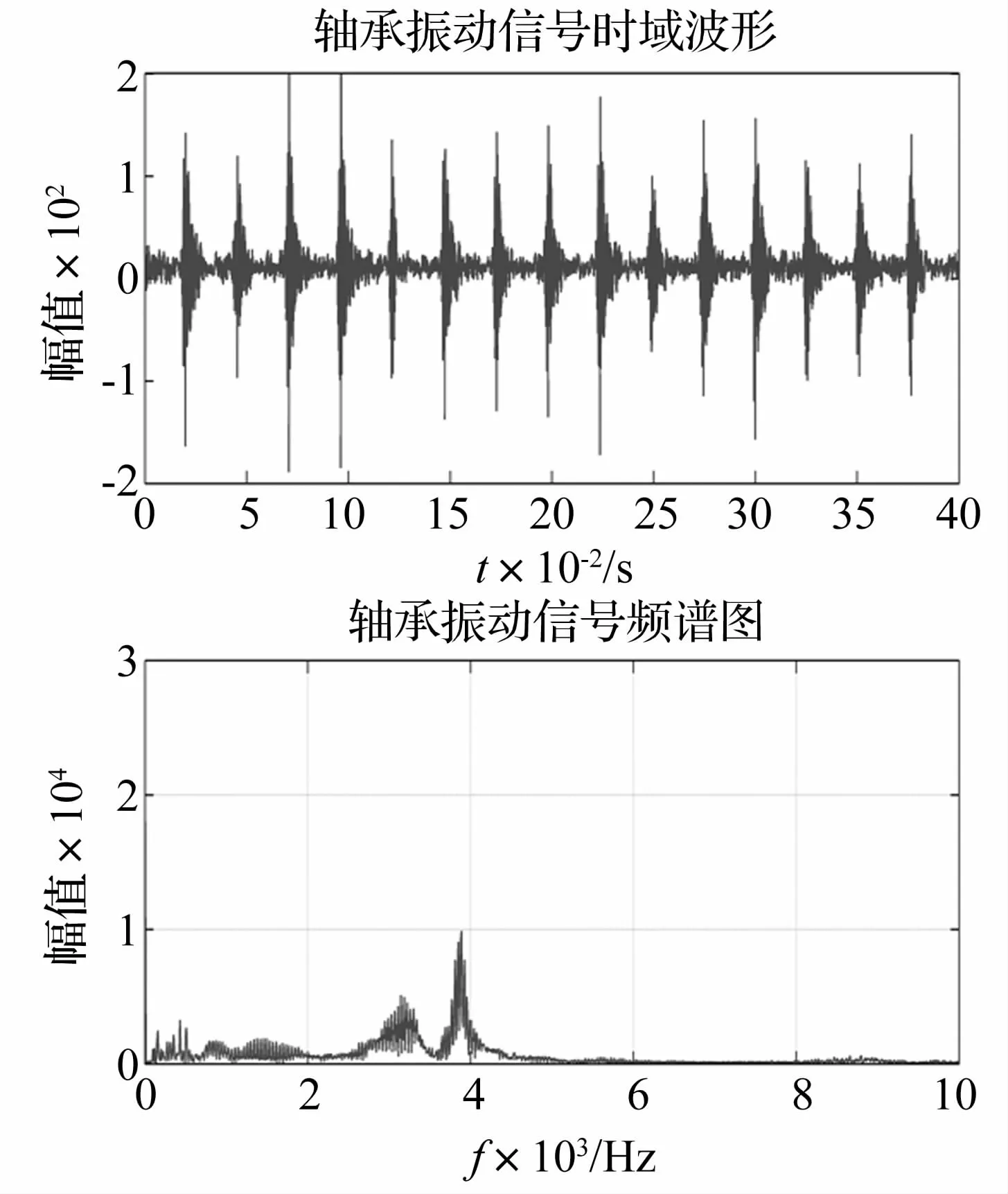
图5 轴承故障信号的时域和包络谱Fig.5 Time-domain diagram and envelope spectrum of signal of fault bearing
从时域波形来看,该信号中含有一定的冲击成分,所以可以初步判定轴承是有缺陷的,但是无法具体判断发生了何种故障。而从包络谱波形来看,故障特征频率处的谱峰也很不明显,难以识别故障。
为了提取该故障信号的特征频率,识别故障类型,首先对故障信号直接进行EMD分解,分解结果如图6所示。
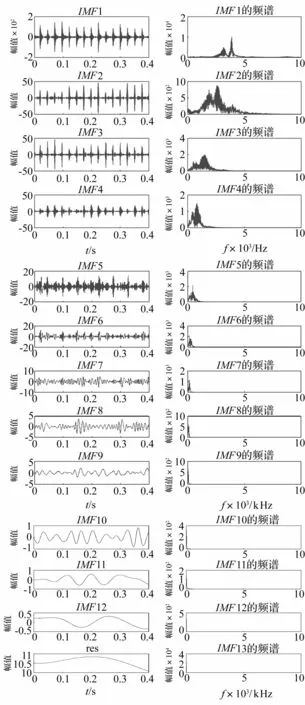
图6 轴承故障信号EMD分解结果Fig.6 The EMD decomposition results of signal of fault bearing
直接用EMD方法对轴承故障信号进行分解,把非平稳的轴承故障振动信号分解成了12个IMF分量及余项。由于IMF分量的能量主要集中在前几个,包含了主要的故障信息,所以只需要提取前几个IMF作为故障模式识别的依据。根据分解结果,发现故障频率存在于第六个IMF分量中,它对应的幅值最大,故障特征最明显,故障特征频率为146.5 Hz。IMF6放大后的包络谱如图7所示。
采用调频EMD方法对该轴承故障信号进行分解,选用调频频率fd=45 Hz,分解得到前五个IMF分量,如图8所示。
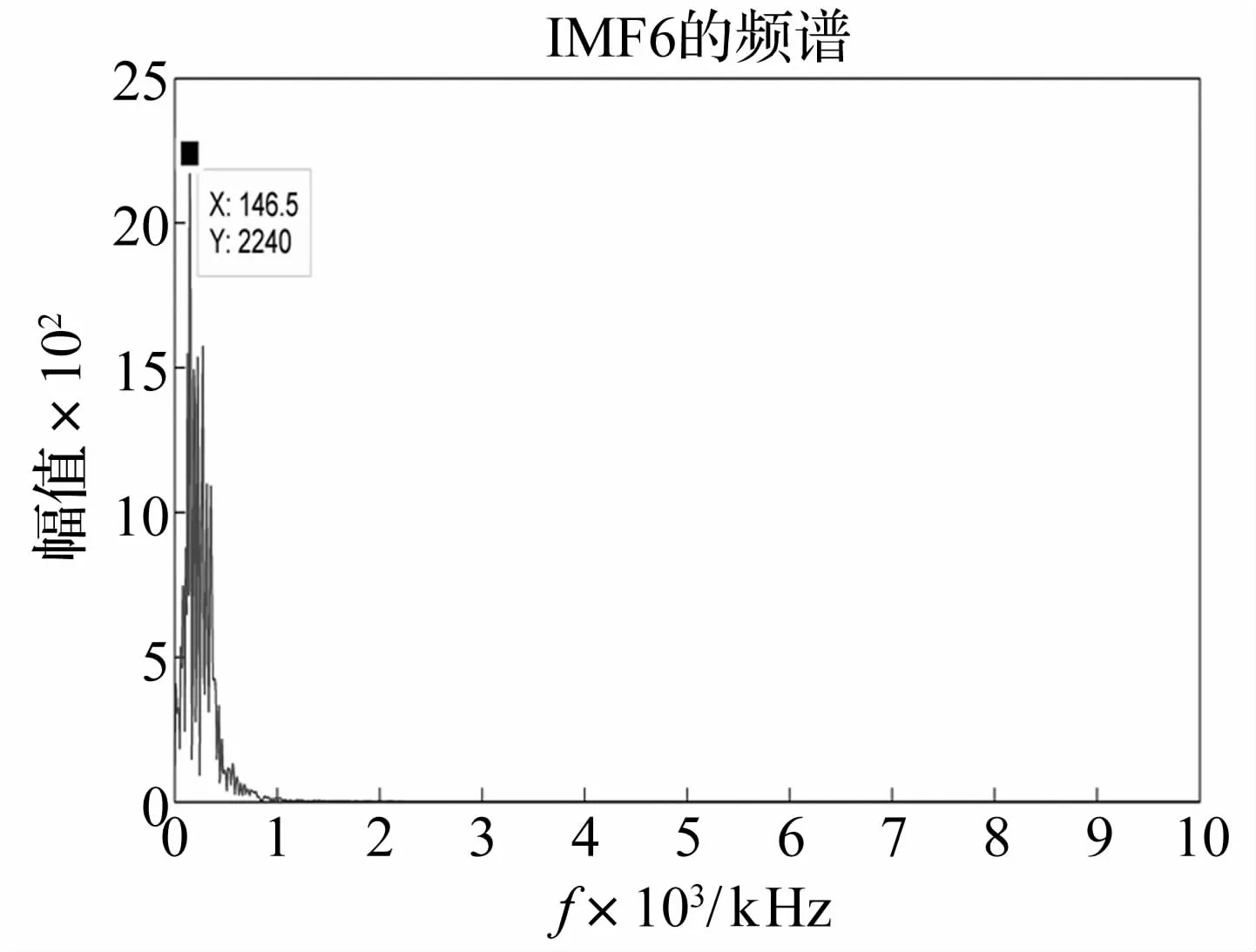
图7 EMD分解的第六个IMF的包络谱Fig.7 Envelope spectrum of IMF 6 in EMD decomposition results
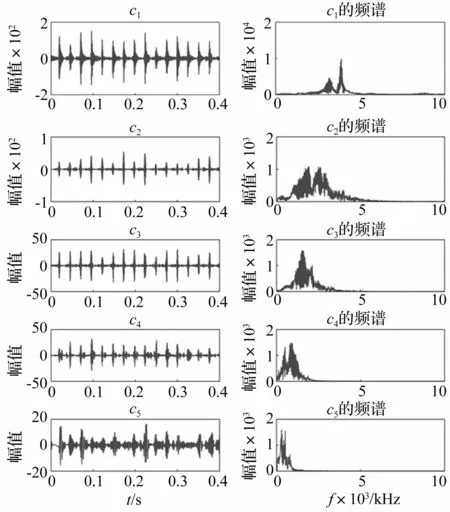
图8 调频EMD分解的前五个IMF分量Fig.8 The first five IMF s in FM-EMD decomposition results
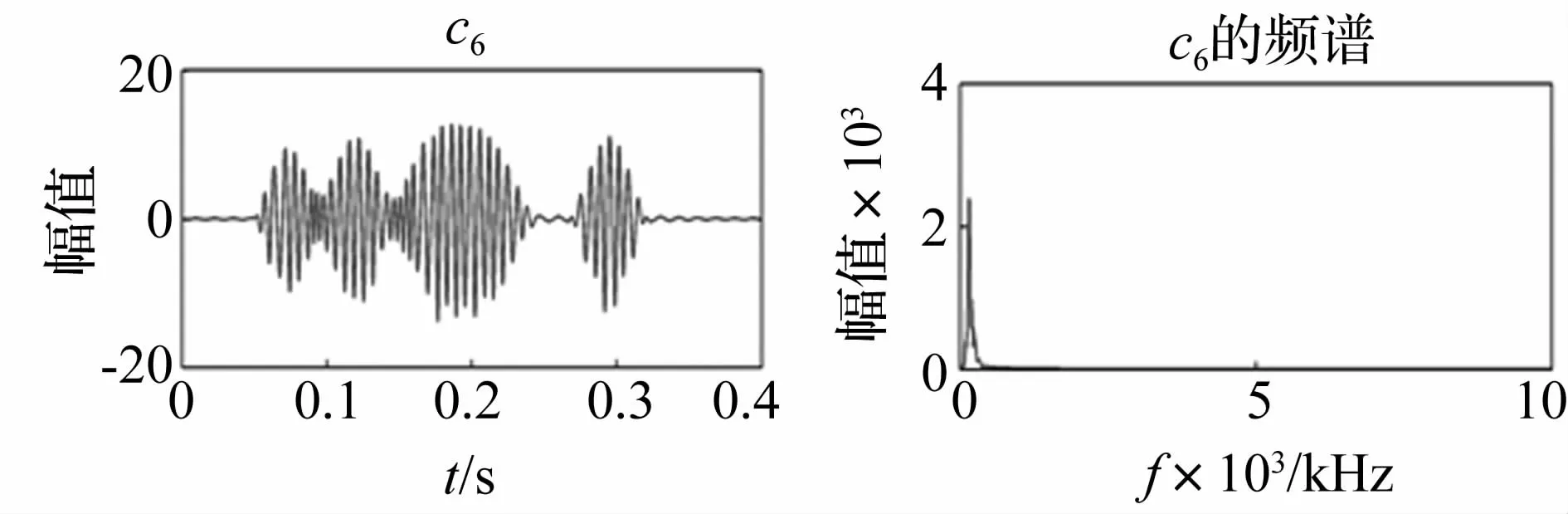
图9 调频EMD分解的第六个IMF分量Fig.9 The sixth IMF in FM-EMD decomposition results
经FM-EMD分解得到的第六个IMF分量如图9所示。将其包络谱图放大后如图10所示。
采用调频EMD方法对轴承故障振动信号进行分解,经包络解调后前几个IMF成分应都能看到故障频率,但是其幅值不是最大,而第六个IMF分量中的故障频率的幅值最大,故障在此积聚的能量最多,所以说可以发现故障信息存在于第六个IMF分量中。在故障频率146.5 Hz处有明显的冲击,与滚动体的故障特征相符合,由此可以判断滚动轴承的故障为滚动体故障。
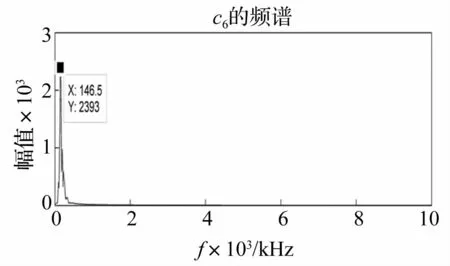
图10 调频EMD分解的第六个IMF分量的包络谱图Fig.10 Envelope spectrum of the sixth IMF in FM-EMD decomposition results
4 结 论
本文对EMD和FM-EMD两种算法进行了数值仿真,并将此两种方法对轴承故障信号进行处理,可得结论:
(1)FM-EMD方法较原 EMD方法能够有效地分解具有相对密集频率成分的弱非线性衰减信号,得到物理意义明确的IMF,且模态混叠程度有了一定的改善。
(2)FM-EMD方法可以应用于轴承故障诊断领域,可以在一定程度上提高故障诊断精度。
[1]张超,陈建军,徐亚兰.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5):539-545.ZHANG Chao,CHEN Jian-jun,XU Ya-lan.A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J].Journal of Vibration Engineering,
2011,24(5):539-545.
[2] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of Royal Society of London,Series A,1998,454:903-995.
[3]张欣,杜修力.基于调频EMD的结构非线性辨识方法研究[J].工程力学,2011,28(8):83-88.ZHANG Xin,DU Xiu-li.Identification of nonlinear system by frequency modulated EMD method[J].Engineer Mechanics,2011,28(8):83-88.
[4]Rilling G,Flandrin P.One or two frequencies?The empirical mode decomposition answers[J].IEEE Transactions on Signal Processing,2008,56(1):85-95.
[5]Wu Z H, Huang N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method[J].Advances In Adaptive Data Analysis,2008,1(1):141.
[6]沈长青,朱忠奎,刘方,等.基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J].振动与冲击,2013,32(2):76-80.SHEN Chang-qing,ZHU Zhong-kui,LIU Fang,et al.Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J].Journal of Vibration and Shock,2013,32(2):76-80.
[7]周智,张优云,朱永生,等.基于EEMD和共振解调的滚动轴承自适应故障诊断[J].振动与冲击,2013,32(2):39-43.ZHOU Zhi,ZHANG You-yun,ZHU Yong-sheng,et al.Adaptive faultdiagnosis of rolling bearings based on EEMD and demodulated resonance[J].Journal of Vibration and Shock,2013,32(2):39-43.
[8]张学清,梁军.基于EEMD-近似熵和储备池的风电功率混沌时间序列预测模型[J].物理学报,2013,62(5):1-10.ZHANG Xue-qing,LIANG Jun.Chaotic time series prediction model of wind power based on ensemble empirical mode decomposition-approximate entropy and reservoir[J].Acta Physica Sinica,2013,62(5):1-10.

