水体防爆墙和混凝土防爆墙对爆炸冲击波的消减效应
张 耀,年鑫哲,严东晋,,孙传怀,王浩舟
(1.解放军理工大学 国防工程学院,南京 210007;2.解放军国际关系学院,南京 210039;3.解放军96155部队,安徽 黄山 245400)
为使重要建筑物能抵抗大当量汽车炸弹的袭击,可在建筑物周围一定范围内构筑防爆墙,其中混凝土防爆墙和水体防爆墙是较为常见的两种防爆墙形式。这两种防爆墙对爆炸冲击波的防护机理截然不同,但二者对冲击波均具有较强的消减作用。毛益明等[1]通过缩比试验与数值模拟相结合的方法对比验证了水体防爆墙与钢筋混凝土防爆墙都具有显著的消波作用。洪武等[2]对国内外水体防爆墙机理研究进展进行了总结归纳,描述了水体防爆墙在受到冲击波作用时的反应过程及爆炸产物、空气和液体之间的能量转化规律。Willauer等[3]在具有通风孔的室内进行了23 kg TNT爆炸实验,对比了在具有水雾条件下等量TNT炸药爆炸的室内冲击波超压、冲量和静态超压的变化,实验表明,水雾的存在可以使TNT炸药室内爆炸产生的冲击波超压、冲量和静态超压分别降低36%,40%和35%。而在工程设计中关心的防爆墙后的流场和压力分布规律与炸药当量、爆炸高度、墙高、墙的高宽比、炸药和墙之间的距离、墙后距离等参数密切相关,要获得具有工程指导意义的规律或公式较为困难,需要基于量纲理论建立工程模型[4],而后进行大量试验和数值模拟。本文期望从物质间能量转化的角度分析两种防爆墙的消波机理,从而帮助研究者加深对两种防爆墙消波机理的认识。
1 两种防爆墙的消波机理[5]
混凝土防爆墙的强度和刚度都很大,经受设计(规定)的爆炸荷载作用时,墙体基本不破坏且变形很小,冲击波流场分析时防爆墙可以近似简化为不动刚体考虑。混凝土防爆墙对爆炸冲击波的防护作用主要通过对冲击波的反射、扰流作用来实现。汽车炸弹爆炸产生的冲击波遇到防爆墙发生反射,不能直射到达防爆墙后的建筑物。实际作用在建筑物上的压力,只是由防爆墙上反射高压区的空气扰流泄压与不规则流动生成,使作用在建筑物上的压力大为衰减。
水体防爆墙属于惯性防爆墙,主要利用水这种就便材料的质量来抵抗爆炸作用。在大当量汽车炸弹袭击下,水体防爆墙中的水受冲击波作用发生飞散,在飞散过程中分散成小颗粒或小水珠(部分水体发生雾化),消耗较多的动能。水体类防爆墙的研究属于非定常气-液两相流问题,冲击波作用下水体的破碎和雾化,冲击波在传播过程中爆炸产物、气体、液体之间能量的相互转化等问题都是揭示水体类防爆墙消波作用机理的重要内容。
2 有限元模型的建立
鉴于所研究问题的复杂性,参考文献[1]的试验,利用AUTODYN软件模拟了227 kgTNT炸药触地爆炸后冲击波受水体防爆墙和混凝土防爆墙阻滞后绕射的情况,对比分析了两种防爆墙的消波效果及物质间的能量转化规律。炸药及防爆墙设置如图1所示。有限元模型为二维轴对称模型。炸药为227 kg球形TNT装药,装药置于地面,中心起爆,炸药距离防爆墙水平距离为 3.0 m,防爆墙水平宽度 0.5 m,高度 2.5 m,有限元中空气域长8.2 m,高4.0 m。模型的左边界和上边界设置为流出边界(flow out),以模拟无限空气域。测点布置如图2所示,下一步对比的测点为8至13号测点,测点距离爆心水平距离为8 m,高度间隔为0.5 m。计算分三步。第一步计算出无防爆墙情况下各个测点的冲击波入射压力及冲量,第二步计算出设置水体防爆墙后测点上的入射压力及冲量,第三步计算出设置混凝土防爆墙后测点上的入射压力及冲量。最后对数据进行整理分析,得出两种防爆墙的消波效果和炸药、空气及墙体间的能量转化规律。

图1 防爆墙设置(cm)Fig.1 The set of the explosion-proof walls

图2 测点设置Fig.2 The set of the gauges
3 材料模型
计算所采用的材料模型均取自AUTODYN自带的材料库。TNT炸药需要定义炸药密度ρ,CJ面压力Pcj及爆轰波速D等参数。采用JWL状态方程来描述爆炸产物压力和内能及相对体积的关系。JWL状态方程形式如下:
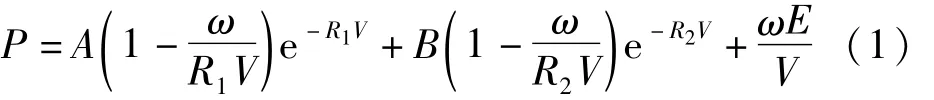
式中:A,B,R1,R2,ω均为材料常数,V为相对体积,E为初始内能密度。炸药主要参数如表1所示。
空气采用理想气体状态方程,选用线性多项式状态方程描述,压力按下式进行计算:
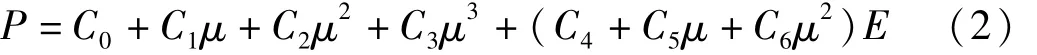
式中 μ=ρ/ρ0-1,ρ/ρ0是当前密度与初始密度的比值。当空气视为理想气体时,C0=C1=C2=C3=C6=0,C4=C5=γ-1。γ是气体的比热容,一般取1.4。空气密度 ρ取1.292 kg/m3,初始内能密度 e0为 0.206 8×106J/m3。
水采用 shock状态方程[6-7]
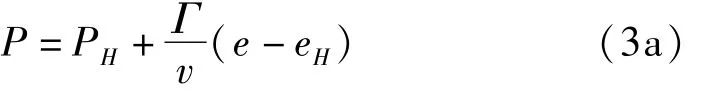
其中:

式中,λ和c0为常数,由以下冲击波实验关系式确定:

式中,D为冲击波速度;u为波后质点速度。取ρ0=0.998 g/cm3,c0=1.647×103m/s,λ=1.921。
混凝土采用 TU Zhen-guo等[8-9]提出的修正的CONC35MPa材料模型,修正后的模型能够更好地反映混凝土在高应变率条件下的动态响应。CONC35MPa模型采用p-α状态方程来描述材料中孔隙在外荷载作用下逐渐塌陷至完全消失的过程。

式中,α是材料的孔隙率,α=v/vs,v是孔隙材料的比容,vs是孔隙材料完全压实后的比容;p是静水压力;pe是材料的初始屈服静水压力;ps是材料完全压实时的静水压力;β是与材料性质有关的指数。混凝土的强度和失效模型采用RHT模型来定义。状态方程及材料强度参数参见文献[8-11]。
4 防爆墙消波效果对比与物质间的能量转化
4.1 主要测点入射压力、入射冲量及超压峰值和冲量峰值消减率对比
图3中第一波次的压力为无墙时各个测点的入射压力,第二波次为有墙条件下各个测点的入射(绕射)
压力,有墙条件下冲击波入射压力到达时间较无墙条件下冲击波入射压力延迟大约4.5 ms。可以看出,水体防爆墙条件下和混凝土防爆墙条件下相同测点的压力到达时间、压力波形及峰值非常接近。表列出三种条件下测点的超压峰值和冲量峰值。定义冲击
波超压峰值消减率冲量消减率 η =1式中,p为无防爆墙时入射超压峰值,p为有sosn
防爆墙时入射超压峰值;Iso为无防爆墙时测点冲量峰值,Isn为有防爆墙时冲量峰值。由表的结果可计算出两种防爆墙对冲击波超压峰值和冲量峰值的消减率(表)。由表看出,按照文献[1]所设定的未缩比工况进行计算,水体防爆墙和混凝土防爆墙均可以起到很好的消波效果,两种防爆墙的消波效果基本接近,文献[1]的试验和计算结果也表明两种防爆墙对爆炸冲击波峰值压力的衰减率均可以达到70%以上。
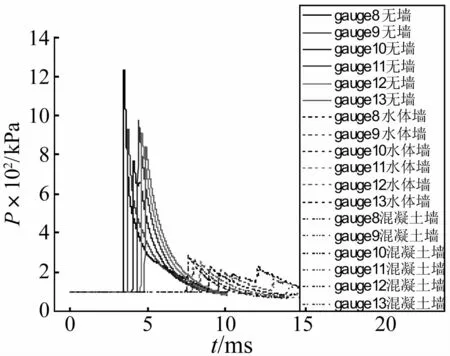
图3 无墙和两种防爆墙条件下距爆心水平距离8 m处测点的压力时程Fig.3 The pressure-time history at the gauges 8m away from the detonation point under the conditions of no walls andthe explosion-proofwalls

表2 三种条件下测点的超压峰值和冲量峰值Tab.2 The peak overpressure and the peak im pulse of the gauges under three conditions

表3 两种防爆墙的消波效果Tab.3 Them itigation effect of the two explosion-proof walls
4.2 各物质间能量转化对比
图4至图6为炸药在无防爆墙条件下、混凝土防爆墙条件下和水体防爆墙条件下的能量分布及转化情况。炸药地面爆炸时,在0.5 ms内爆炸产物的内能迅速下降,动能迅速增长,空气的内能和动量在逐渐增长,这时是冲击波形成的初期。随着空气冲击波传播的衰减,空气的动能逐渐转化为空气的内能,爆炸能量最终以内能的形式储存于空气中(图4)。当水体防爆墙存在时,爆炸冲击波在接触水体时发生反射,爆炸产物受到水体的阻滞(图7),爆炸产物的内能出现反弹,此时空气内能由增长趋势变为下降趋势。随着水体的解体、雾化、汽化等一系列反应的发生,爆炸产物的内能随之减小,爆炸的能量又转化为空气的内能和水体的动能、内能,各物质的能量之间也在整个过程中不断转化(图5)。当混凝土防爆墙存在时,爆炸冲击波遇墙面受到阻滞并在瞬间发生反射(图8),爆炸产物的内能、动能和空气的内能、动能相互转化的趋势与水体防爆墙存在时各物质能量的变化趋势基本相同(图6),在计算结束时刻,空气内能在总能量中所占的份额(约83%)较水体防爆墙存在时空气内能的份额多(约65%),混凝土防爆墙自身获得的内能、动能在总能量中所占的份额很少,这说明防爆水体对降低空气内能起到更加显著的作用。对比图7和图8可看出,主要是迎爆面的水体与冲击波及爆炸产物发生了能量交换,导致这部分水体的内能有较为显著的增长,而混凝土与冲击波和爆炸产物的能量交换不明显,防爆墙前面的空气与爆炸产物间的能量交换更加显著。
从表4中看出,混凝土在能量交换过程中获得的总能量峰值比水体小大约一个量级,占炸药能量比例水体获得的总能量峰值占炸药能量的比例也不是很大,约100%=6.84%,这说明除了水体本身耗散掉小部分爆炸产物和空气冲击波的能量之外,更多的是依靠水体本身的质量和惯性实现对爆炸冲击波的阻滞和反射来实现保护墙体后部目标的目的。
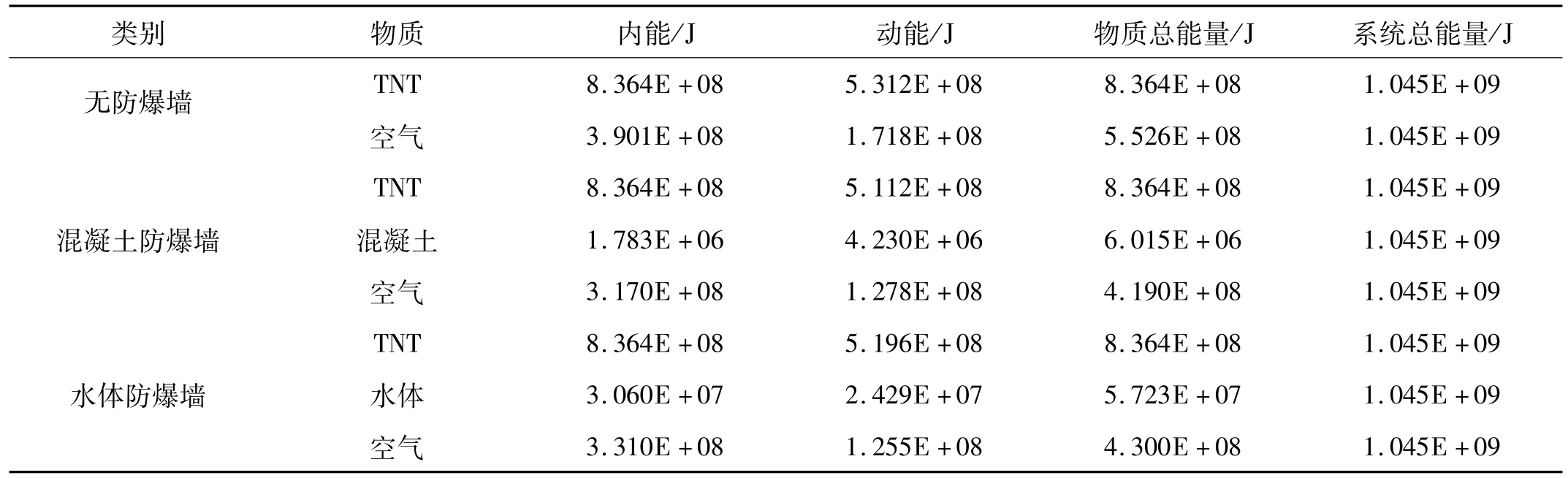
表4 三种条件下各物质的能量峰值Tab.4 The peak energy of each substance under the three conditions

图4 无防爆墙条件下各物质的能量分布Fig.4 The energy distribution of the substances(no wall)
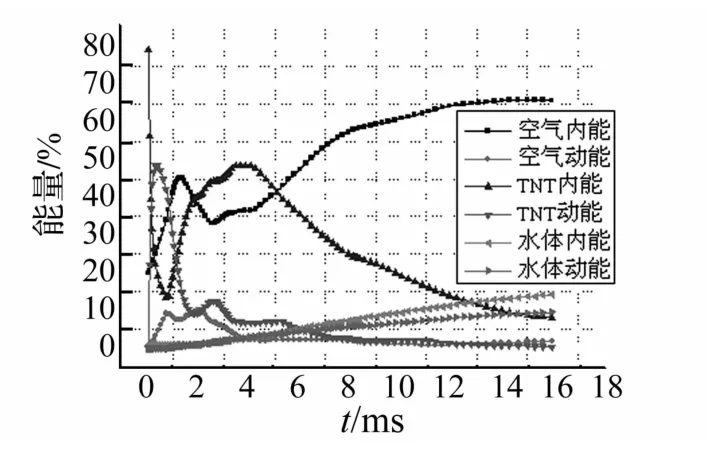
图5 水体防爆墙条件下各物质的能量分布Fig.5 The energy distribution of the substances(explosion-proofwater wall)
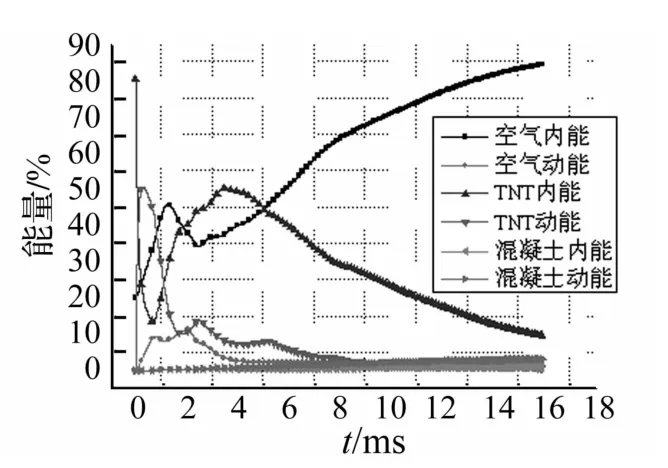
图6 混凝土防爆墙条件下各物质的能量分布Fig.6 The energy distribution of the substances(concrete wall)

图7 水体防爆墙与冲击波反应时体系的内能变化Fig.7 Change in internal energy of the system when the explosion-proofwater walls is reacting with the blastwave

图8 混凝土防爆墙与冲击波反应时体系的内能变化Fig.8 Change in internal energy of the system when the explosion-proof concrete walls is reacting with the blastwave
4.3 不同药量下水体防爆墙和混凝土防爆墙的消波效果和能量变化
计算得到了 25 kg,50 kg,100 kg,150 kg,227 kg五个药量条件下水体墙能量和混凝土墙能量的变化,炸药爆心距离墙迎爆面的水平距离均为3 m,水体墙和混凝土墙厚度均为50 cm,测点位置见图2。五种药量下水体墙和混凝土墙的消波率见表5。
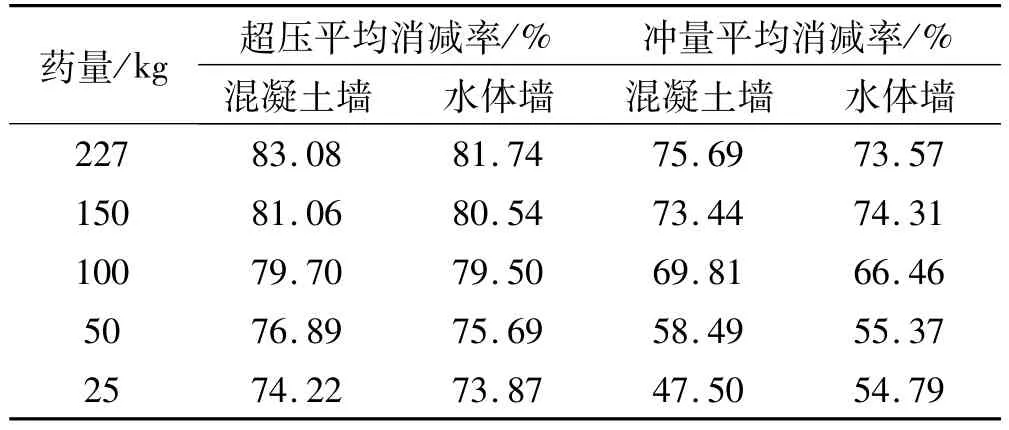
表5 不同药量的计算结果Tab.5 The results of different exp losivemass
从表中看出,药量越小,墙后相同测点上的超压消减率和冲量消减率越小。实际上,随着药量减小,炸药距离墙体迎爆面的比例距离r和测点距离墙体后面的比例距离,墙体的比例高度都在变大。根据丁娜娜等[12]对钢筋混凝土防爆墙消波效应的研究,对于一定厚度的混凝土墙体而言值与消波率大致成正比值和值与消波率大致成反比。水体墙与混凝土墙不同之处在于水体墙受爆炸波作用时会发生解体和飞散,所以三个参数对水体墙的消波率如何影响还需要进一步研究。
图9为几种工况下水体能量和混凝土能量占炸药能量份额随药量变化的情况。横坐标代表炸药质量,纵坐标代表水体和混凝土墙体获得的能量峰值Ep与炸药能量Et的比值。
从图9看出,混凝土获得的能量在炸药能量中所占份额随药量增加而增加,增加趋势几乎是线性的。混凝土获得的能量非常少,占炸药能量的最大份额不超过炸药能量的0.8%。而水体获得的能量在炸药能量中所占份额随着药量变化呈现出一定的波动,其中水体获得的内能所占炸药能量份额大致是随着药量增加先增大后减小,动能所占份额则随药量增加而增加。

图9 水体和混凝土能量份额随药量变化Fig.9 The propotion ofwater and concrete energy varieswith themass of explosives
5 影响水体墙消波效果的主要因素
水体对冲击波的消波效应主要与水体与炸药的质量比,水体墙厚度d以及炸药与水体墙之间的比例距离有关[13]。为此设置不同工况考察上述参数对水体墙消波作用和能量变化的影响。测点位置见图2。
5.1 水体与炸药质量比对消波率的影响
水体墙与炸药之间距离不变,改变墙体厚度,计算得到不同工况下墙体后部测点上的压力并得到平均超压消减率和平均冲量消减率,计算结果见表6。
表中,c为炸药质量,r为炸药与水体墙间的水平距离为炸药与水体墙间的水平比例距离,d为墙体厚度,cw为水体质量,ηp为测点的平均超压消减率,ηⅠ为测点的平均冲量消减率,Ew为水体获得的总能量峰值,Et为炸药能量。
从表6的结果看,炸药与水体间距离一定,当水体墙厚度(水体与炸药质量比)减小时,墙后测点处的超压消减率和冲量消减率逐渐减小,其中超压消减率减小幅度并不大,当墙体厚度小于10 cm时,冲量消减率有了显著的减小。这是由于水体墙后部测点(测点距离地面高度2 m)处的压力有两个峰值(图10),第一峰值是绕射压力峰值,第二压力峰值是绕射波绕过墙体后传播遇到地面反射引起,尽管水体墙厚度小于10 cm后对第一压力峰值影响不大,但水体墙水体墙厚度减小会导致测点处反射压力峰值(第二个压力峰值)有所增加,导致测点处冲量增加。当水体墙厚度为2.5 cm时,超压消减率和冲量消减率均有明显减小,这是因为此时水体墙被冲击波冲散,而后受水体阻滞的冲击波直接到达测点使得墙后测点的超压有了较大幅度的提升。水体墙获得的能量是随着墙体厚度的减小和水体炸药质量比的减小而逐渐增加的,水体炸药质量比越小,水体越能够从炸药中获得能量。25 cm厚的水体墙和50 cm厚的水体墙消波率几乎一样,说明并不是水的质量越多消波效果越好,而应该在实际应用中根据炸药量合理配置水体质量。
5.2 水体墙与炸药之间比例距离对消波率的影响
保持水体与炸药质量比不变,改变水体墙与炸药间的距离,计算得到不同工况下相同测点上的压力并得到平均超压消减率和平均冲量消减率(表7),测点位置见图2。

表7 不同比例距离的计算结果Tab.7 The results of water walls for different scaled distances
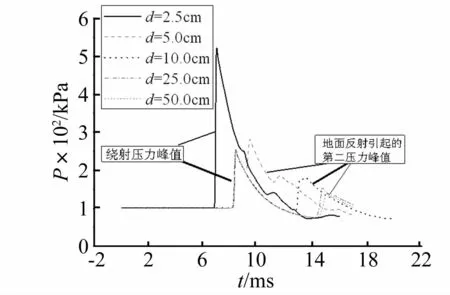
图10 不同厚度水体墙后部测点压力Fig.10 The pressure-time history at the gaugeswarieswith thicknesses ofwater walls
由计算结果可知,在水体与炸药质量比一定的条件下,改变水体与炸药之间的比例距离变化对削波率没有很大的影响,水体与炸药间水平距离为为3 m时,消波效果略好一些。水体墙与炸药之间水平比例距离越远,作用于水体上的冲击波压力越小,继而水体发生解体和飞散的程度减小,水体与冲击波和爆炸产物间能量交换减弱,导致水体获得的能量减小。从图11看出,随着水体墙与炸药间比例距离的增加,水体墙后测点(测点距离地面高度2 m)处的绕射压力峰值略有增大,而绕射引起的反射压力峰值逐渐减小。
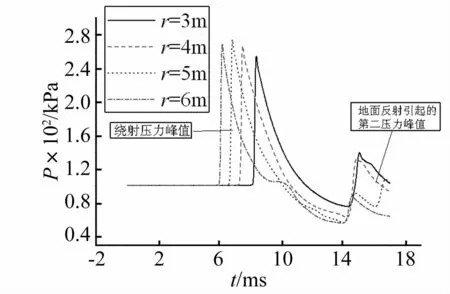
图11 水体与炸药距离改变后墙后测点压力Fig.11 The pressure-time history at the gauges varies with distances between water and explosives
6 结 论
本文针对的TNT炸药地面爆炸形成冲击波后遇防爆墙作用后爆炸波被消减的情况进行了计算,对两种防爆墙的消波效果进行了对比,得到了无防爆墙、设置水体防爆墙和设置混凝土防爆墙三种工况下物质间能量转化的时程曲线。对结果分析可以得出以下结论:
(1)水体防爆墙如果设置合理,具有和混凝土防爆墙一样的消波效果。
(2)两种防爆墙条件下爆炸产物内能、动能和空气内能、动能的时程曲线变化规律基本相似。
(3)水体防爆墙在受冲击波作用时迎爆面的水体相比被爆面的水体从冲击波和爆炸产物中获得了更多的内能。
(4)水体防爆墙在与爆炸波相互作用的整个过程中获得的总能量峰值比混凝土防爆墙大一个量级。混凝土防爆墙在与爆炸波相互作用的过程中获得的总能量峰值占炸药能量比例非常少,大致在0.8%以下。
(5)水体防爆墙自身耗散掉爆炸产物和冲击波的能量有限,更多的是依靠水体的质量和惯性实现防爆的目的。
(6)水体与炸药的质量比对水体消波效果有一定影响,水体与炸药质量比越大,水体对冲击波冲量的消减作用越强。
[1]毛益明,方秦,张亚栋,等.水体与混凝土防爆墙消波减爆作用对比研究[J].兵工学报,2009,S2:84-89.MAO Yi-ming, FANG Qin, ZHANG Ya-dong, et al.Comparison investigation on mitigation effect of water and concrete explosion-proof walls[J].Acta ArmamentarⅡ,2009,S2:84-89.
[2]洪武,徐迎,金丰年.水体防爆机理研究进展[J].防护工程,2011,33(3):73-78.HONGWu,XU Ying,JIN Feng-nian.Development of blast-resistantwaterwalls[J].Protective Engineering,2011,33(3):73-78.
[3]Willauer H D,Ananth R,Farley J P,et al.Mitigation of TNT and destex explosion effects using water mist[J].Journal of Hazardous Materials,2009,165(1-3):1068-1073.
[4]任新见,张庆明,薛一江.坑道口部B炸药爆炸冲击波传播速度模型试验研究[J].振动与冲击,2012,31(7):71-73.REN Xin-jian,ZHANG Qing-ming,XUE Yi-jiang.Scale model tests to determine in-tunnel blast impact wave velocity for B-charges at tunnel entrance[J].Journal of Vibration and Shock,2012,31(7):71-73.
[5]严东晋,丁娜娜,陈灿寿,等.建筑物外部防爆墙的分类及相关问题[J].防护工程,2006,28(2):68-74.YAN Dong-jin, DING Na-na, CHEN Can-shou, et al.Classification of exterior explosion-proof walls and related issues.[J].Protective Engineering,2006,28(2):68-74.
[6]肖秋平.水下爆炸过程及浅水效应数值模拟研究[D].南京:南京理工大学,2008.
[7]刘科种,徐更光,辛春亮,等.AUTODYN水下爆炸数值模拟研究[J].爆破,2009,26(3):18-21.LIU Ke-zhong,XU Geng-guang,XIN Chun-liang,et al.Research on numerical simulation in underwater explosion by AUTODYN[J].Blasting,2009,26(3):18-21.
[8]TU Zhen-guo,LU Yong.Evaluation of typical concrete materialmodels used in hydrocodes for high dynamic response simulations[J].International Journal of Impact Engineering,2009,36(1):132-146.
[9]TU Zhen-guo,LU Yong.Modifications of RHTmaterialmodel for improved numerical simulation of dynamic response of concrete[J].International Journal of Impact Engineering,2010,37(10):1072-1082.
[10]李小雷,聂建新,覃剑锋,等.含铝炸药在混凝土中爆炸效应的数值模拟研究[J].爆破,2012,29(3):109-114.LIXiao-lei,NIE Jian-xin,QIN Jian-feng,et al.Numerical simulation of explosion effects in concrete by aluminized explosives[J].Blasting,2012,29(3):109-114.
[11]AUTODYN User Manual Version 6.1 [Z]. Century Dynamics Inc,2005.
[12]丁娜娜,严东晋,徐源.悬臂式防爆墙消波作用数值分析及其应用[J].地下空间与工程学报,2010,6(3):645-648.DING Na-na,YAN Dong-jin,XU Yuan.Numerical analysis and application of shielding effect of cantilever blastwall[J].Chinese Journal of Underground Space and Engineering,2010,6(3):645-648.
[13]Cheng M,Hung K C,Chong O Y.Numerical study of water mitigation effects on blastwave[J].Shock Waves,2005,14(3):217-223.

