角接触球轴承的动态参数建模与试验研究

王连宝，胡小秋，冯朝晖，杨 尧

（南京理工大学 机械工程学院，南京 210094）

高档数控机床的主轴系统、进给系统必须具有良好的动态特性［1－2］。角接触球轴承作为机床常用的支承部件，其动态特性是主轴和进给系统的薄弱环节，直接影响着系统整体的动力学性能，因此研究角接触球轴承的动态特性具有重要意义。

对于角接触球轴承的动态特性，国内外学者已经做了大量研究，但大多研究集中在提出和求解不同的力学分析模型［3－10］，这些分析模型基于许多假设，如Hertz弹性接触理论、刚性套圈理论和滚道控制理论等，并不能获取轴承在实际工况下的动态特性数据；少数学者分析了转速、间隙等因素对轴承或转子系统稳定性、振动特性的影响［4，11］，而对轴承的动态刚度和阻尼特性试验分析，涉及较少。应用试验研究不同的载荷条件对角接触球轴承动态刚度和阻尼特性的影响具有重要的价值。

本文忽略了轴承径向与轴向动态参数之间的耦合影响，建立了考虑基础响应的单自由度动态参数测试模型。试验采用正弦扫频激励方式，忽略激振力（远小于轴承的外加载荷）对轴承动态参数的影响，所以外载不变时可以将轴承系统简化为线性时不变模型。

1 轴承动态参数建模

在实际应用中，角接触球轴承普遍成对使用，搭建的试验装置采取一对轴承“背靠背”安装。以轴承组件为研究对象，主要包括心轴、一对轴承和一对轴承套等。轴承内圈与心轴之间、外圈与轴承套之间均采用过盈配合，且心轴的长径比小（即心轴自身弯曲的模态频率较高），可将过盈配合面作固定结合面来处理，将心轴视为质量块（即刚体）。由于固定结合面刚度数量级比滚动结合面高出1～2个数量级，因此本文建立的参数识别模型仅考虑轴承滚动结合面。目前，在机床结构的动态特性分析中，结合面接触特性一般采用数个粘弹性弹簧阻尼单元等效代替，本文的轴承滚动结合面接触特性也采用粘弹性单元处理。

1.1 径向动态参数识别模型

当施加轴向力Fa（即预紧力）、径向力Fr1与Fr2时，左右轴承滚动结合面可以这样处理：在轴承径向中性面上，内外套圈之间均匀布置4个相同的弹簧阻尼单元。轴承的径向动态参数等效模型如图1所示。

图1 轴承径向动态参数等效模型Fig．1 Radialdynamic parameters equivalentmodel of bearing

若Fr＝Fr1＝Fr2，则左右轴承受力状况一致，此时左右轴承的动态特性是相同的，即：单元刚度Kr1＝Kr2，单元阻尼Cr1＝Cr2。当模态试验激励位置位于心轴几何中心P处，根据弹簧的并联关系，可以将参数识别模型进一步简化为考虑基础（轴承套）响应的单自由度径向动态参数测试力学模型，如图2所示。

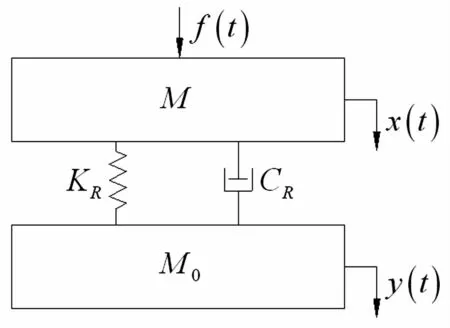
图2 轴承径向动态参数测试力学模型Fig．2 Radialmechanicalmodel for testing dynamic parameters of bearing

当心轴受到简谐激振力f（t）作用时，其振动微分方程可以表述为

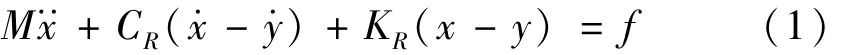
式中：M为心轴、轴承内圈和一半轴承滚珠的质量之和，KR、CR分别为轴承组件滚动结合面的径向动态刚度和阻尼，x、y分别为心轴、基础（轴承套）的径向响应位移。

对式（1）进行以下傅里叶变换：x＝X（ω）ejωt，y＝Y（ω）ejωt，f＝F（ω）ejωt，可得

令式（2）左边为 H（ω），HY（ω）＝Y（ω）／F（ω），HX－Y（ω）＝（X（ω）－Y（ω））／F（ω），则由质量 M、刚度KR、阻尼CR组成的单自由度振动系统位移频响函数H（ω）可以表述为

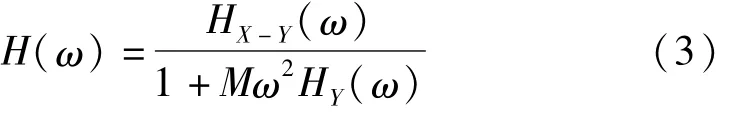
式中：HX－Y（ω）为心轴与基础的频响函数矢量差，HY（ω）为基础位移频响函数。

因此，轴承组件滚动结合面的径向刚度KR和阻尼CR可由下式得到

式中：固有频率ωn、阻尼比ξ为H（ω）的对应模态峰值频率和模态阻尼比，由式（3）识别获取。

由于两个轴承的并联关系，所以单个轴承的径向刚度KR0和阻尼CR0可以表述为

1.2 轴向动态参数识别模型

与径向动态参数等效模型类似，轴承的轴向动态参数等效模型如图3所示。

图3 轴承轴向动态参数等效模型Fig．3 Axial dynamic parameters equivalentmodel of bearing

图4 轴承轴向动态参数测试力学模型Fig．4 Axialmechanicalmodel for testing dynamic parameters of bearing

当左右轴承受力状况相同时，轴承的轴向动态参数识别模型可以简化为考虑基础（轴承套）响应的单自由度轴向动态参数测试力学模型，如图4所示。

同样地，可得由质量M、刚度KA、阻尼CA组成的单自由度振动系统位移频响函数H（ω）为

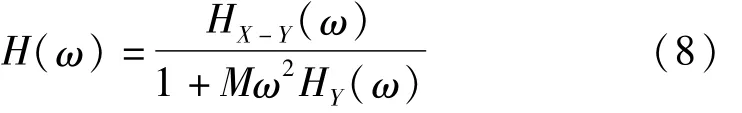
式中：HX－Y（ω）、HY（ω）与式（3）意义相同。

因此，轴承组件滚动结合面的轴向刚度KA和阻尼CA可以由下式得到

式中：固有频率ωn、阻尼比ξ为H（ω）的对应模态峰值频率和模态阻尼比，由式（8）识别获取。

单个轴承的轴向刚度KA0和阻尼CA0可以表述为

2 试验部分

2.1 试验装置

试验装置由两部分组成：一是机械部分，主要由轴向加载机构1、轴承组件4、径向加载机构5、轴承座体和基板等构成；二是测试部分，采用南京安正公司研制的CRAS模态分析系统和北京昆仑公司生产的静力测试系统，主要包括加速度传感器2、径向激振器3、力传感器6、轴向激振器7、安装CRAS软件的计算机8、信调仪9、数采器10、功率放大器11和CHB数显表12等。其中，轴向加载机构1采用不同旋向的双螺杆结构。图5为轴承轴向模态试验的实物图。

图5 轴承动态参数测试试验装置Fig．5 Test device for testing dynamic parameters of bearing

2.2 模态试验

利用自主搭建的试验装置，测试了NSK系列5组轴承（NSK 30TAC 62A，NSK 35TAC 72A，NSK 40TAC 72A，NSK 45TAC 75A，NSK 50TAC 100A），分别测试了较大范围内的径向载荷与轴向载荷作用时轴承的轴向、径向动态刚度和阻尼。与文献［8－9］对比，本文的试验曲线与文献值趋势一致。

3 试验结果及讨论

3.1 轴向载荷对动态特性的影响

图6～7分别为NSK 50TAC 100A轴承的轴向刚度KAO、轴向阻尼CAO和径向刚度KRO、径向阻尼CRO随轴向载荷Fa的变化情况。

从图6可以看出，随着Fa的增大，KAO、KRO逐渐增大，但增幅越来越小；当Fa达到一定值时，Fa的进一步增加对KAO、KRO的影响不大。这是因为：两个表面接触时，其实际接触发生在两个表面上的一些微凸体之间［12］。当Fa较低（即轴承滚动结合面法向载荷较低）时，结合面间的实际接触发生在少数较高的微凸体顶端之间，此时结合面法向动刚度较小，其轴向、径向的刚度分量也较小，故KAO和KRO较低；当Fa较高时，一方面发生实际接触的微凸体增多，另一方面已发生接触的微凸体进一步变形，其接触面积也随之增大，二者综合作用的结果使结合面的实际接触面积增大，从而结合面法向动刚度增大，故KAO和KRO逐渐增大；由于在一定的Fa下，实际接触面积的大小与接触变形量成反比，所以随着Fa的增大，实际接触面积增速越来越慢，故KAO和KRO增幅逐渐减小；当Fa达到一定值时，Fa的进一步增加对实际接触面积的增大影响很小，所以KAO和KRO趋于某值。

从图7可以看出，随着Fa的增大，CAO、CRO先减小后增大。这是因为：承受动载荷的两个表面接触会产生库伦摩擦阻尼和结合面阻尼，前者源于结合面之间宏观相对滑动的干摩擦耗能，后者是接触区局部塑性应变（微观相对滑移）而产生的能量损耗［13］。当Fa较低时，实际接触的微凸体较少，且其顶部分主要产生弹性变形，结合面易于产生宏观相对滑动，此时结合面以库伦摩擦阻尼耗能为主，结合面阻尼影响较小；随着Fa的增大（仍然较低），结合面仍以库伦摩擦耗能为主，但能力降低，所以结合面法向阻尼会减小，故CAO和CRO会逐渐减小；当Fa较高时，接触的微凸体增多，且其顶部分达到屈服强度而产生了塑性变形，在动载荷（激振力）作用下结合面之间发生微观相对滑移，此时结合面以结合面阻尼耗能为主，随着Fa的增大，接触区愈来愈多的微凸体接触且发生塑性变形，结合面阻尼的耗能能力逐渐增强，所以CAO和CRO逐渐增大。

图6 轴向载荷对刚度的影响曲线Fig．6 Influencing curve of axial load on the stiffness

图7 轴向载荷对阻尼的影响曲线Fig．7 Influencing curve of axial load on the damping

图8 径向载荷对刚度的影响曲线Fig．8 Influencing curve of radial load on the stiffness

3.2 径向载荷对动态特性的影响

图8～9分别为NSK 50TAC 100A轴承当轴向载荷Fa＝3 500 N时轴承的轴向刚度KAO、轴向阻尼CAO和径向刚度KRO、径向阻尼CRO随径向载荷Fr的变化情况。

从图8可以看出，随着Fr的增大，KAO、KRO逐渐增大，但增幅越来越小。这是因为：当 Fr作用时，轴承内、外圈之间产生相对径向位移，上半圈滚珠接触变形量会减小，下半圈滚珠接触变形量会增大，而结合面的综合法向动刚度会增大，故KAO和KRO逐渐增大；随着Fr的进一步增大，上、下半圈结合面的实际接触面积之和增长趋缓，故KAO和KRO增幅逐渐减小。

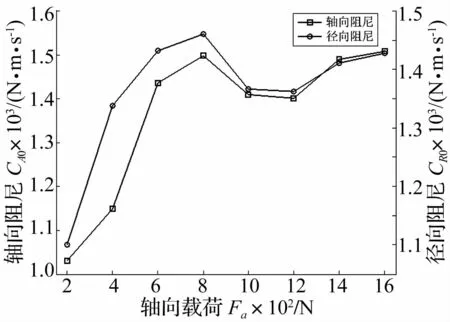
图9 径向载荷对阻尼的影响曲线Fig．9 Influencing curve of radial load on the damping

从图9可以看出，随着Fr的增大，CAO、CRO先增大后减小再增大。这是因为：据图7知，当Fa＝3 500 N时轴承以结合面阻尼为主要的能量耗损方式；当Fr在一定范围内增长时，轴承结合面耗能方式以结合面阻尼为主，上、下半圈结合面法向阻尼分别减小、增大，而结合面的综合法向阻尼会增大，故CAO和CRO会逐渐增大；当Fr继续增大，轴承结合面耗能发生变化——上、下半圈分别以库伦摩擦阻尼、结合面阻尼为主，而上半圈结合面耗能能力减小量大于下半圈结合面的增加量，即结合面的综合法向阻尼会减小，故CAO和CRO在该阶段将逐渐减小；当Fr进一步增大，上、下半圈结合面的实际接触面积分别继续减小、增大，此时上半圈结合面耗能能力减小量小于下半圈结合面的增加量，即结合面的综合法向阻尼会增大，故CAO和CRO将再次趋于增大。

4 结 论

（1）本文搭建了角接触球轴承动态参数识别试验装置，采用粘弹性弹簧阻尼单元等效轴承滚动结合面，提出了考虑基础响应的单自由度动态参数测试力学模型，识别角接触球轴承在不同轴向载荷Fa、径向载荷Fr工况下的动态特性参数；

（2）当Fr＝0 N时，随着Fa的增大，轴承的轴向刚度KAO和径向刚度KRO逐渐增大，且增幅逐渐减小；轴向阻尼CAO和径向阻尼CRO先增大后减小；

（3）当Fa一定时，随着Fr的增大，轴承的轴向刚度KAO和径向刚度KRO逐渐增大，且增幅逐渐减小；轴向阻尼CAO和径向阻尼CRO先增大后减小再增大。

［1］刘强，李冬茹．国产数控机床及其关键技术发展现状及展望［J］．航空制造技术，2010，10：26－30．LIU Qiang，LIDong-ru．Current situation and prospectof key technologies of domestic NC machine tool［J］．Aeronautical Manufacturing Technology，2010，10：26－30．

［2］Abele E，Altintas Y，Brecher C．Machine tool spindle units［J］．CIRP Annals-Manufacturing Technology，2010，59（2）：781－802．

［3］Hagiu G D，Gafitanu M D．Dynamic characteristics of high speed angular contact ball bearings［J］．Wear，1997，211（1）：22－29．

［4］Han D C，Choi SH，Lee Y H．The nonlinear and ball pass effects of a ball bearing on rotor［J］．International Journal，1998，12（3）：396－404．

［5］Hernot X，Sartor M，Guillot J．Calculation of the stiffness matrix of angular contact ball bearings by using the analytical approach［J］．JournalofMechanical Design，2000，122（1）：83－90．

［6］Alfares M A，Elsharkawy A A．Effects of axial preloading of angular contact ball bearings on the dynamics of a grinding machine spindle system［J］．Journal of Materials Processing Technology，2003，136（1）：48－59．

［7］李松生，陈晓阳，张钢，等．超高速时电主轴轴承的动态支承刚度分析［J］．机械工程学报，2006，42（11）：60－65．LI Song-sheng，CHEN Xiao-yang，ZHANG Gang，et al．Analysis of Dynamic supporting stiffness about spindle bearings at extra high-speed in electric spindles［J］．Chinese Journal of Mechanical Engineering，2006，42（11）：60－65．

［8］Jedrzejewski J，Kwasny W．Modelling of angular contact ball bearings and axial displacements for high-speed spindles［J］．CIRP Annals-Manufacturing Technology，2010，59（1）：377－382．

［9］方兵，张雷，曲兴田，等．角接触球轴承动力学建模与实验［J］．农业机械学报，2012，43（6）：215－219．FANG Bing，ZHANG Lei，QU Xing-tian，et al．Dynamic modeling and experiment of angular contact ball bearing［J］．Transactions of the Chinese Society for Agricultural Machinery，2012，43（6）：215－219．

［10］曹宏瑞，李兵，陈雪峰，等．高速主轴离心膨胀及对轴承动态特性的影响［J］．机械工程学报，2012，48（19）：59－64．CAO Hong-rui，LIBing，CHEN Xue-feng，et al．Centrifugal expansion of high-speed spindle and its influences on bearing dynamic characteristics［J］．Chinese Journal of Mechanical Engineering，2012，48（19）：59－64．

［11］Cao H R，Holkup T，Altintas Y．A comparative study on the dynamics of high speed spindles with respect to different preload mechanisms［J］． The International Journal of Advanced Manufacturing Technology，2011，57（9－12）：871－883．

［12］张学良．机械结合面动态特性及应用［M］．北京：中国科学技术出版社，2002：60－61．

［13］戴德沛．阻尼技术的工程应用［M］．北京：清华大学出版社，1991：26－30．