带有温度梯度的热载荷与声载荷作用下薄板动态响应
沙云东,朱 林,栾孝驰,张国治,冯飞飞
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
高超声速飞行器在飞行过程中承受着严酷的航空动力加热。为了维持高温环境下结构的强度,高超飞行器的结构设计要求不同于低马赫数飞行器。依据工作的温度范围,飞行器结构可被称之为热结构。由高温合金设计而成的热结构能够在1 000至1 500高温范围内工作。若热结构由C/C复合材料制造,则工作温度可高达3 000。典型的高超飞行器热结构部件包括:由单片钛合金或金属基复合材料制造而成的加筋板;由超级合金制造而成的蜂窝夹芯板以及C/C复合材料所制造而成的升降舵补助翼(或者襟翼)[1]。承受外部加热的薄金属板在其厚度方向存在较小的温度梯度。然而,即便是在均匀的外部加热条件下,由于支撑结构充当散热片的角色,壁板表面也会存在空间温度梯度分布。因此,典型的结构壁板在其中心承受
着较高的温度,而在与支撑结构相连处温度较低。这些温度梯度结合壁板的初始缺陷,并通过压缩薄膜应力的作用从而引发结构发生热屈曲现象[2]。Ko[3-5]广泛地研究了热结构壁板(无散热片作用)在均匀热载荷条件下的热屈曲问题。Thornton等[2]用有限单元法描述薄板由空间温度梯度作用而引发的屈曲现象。并研究了稳态与非稳态温度分布下薄板的弹性热屈曲特性。Javaheri等[6]研究了不同温度分布下薄板的热屈曲的特性,并利用PDE/Galerkin法推导出了薄板在一维线性温度梯度热载荷作用下的临界热屈曲温度差。不仅是受热载荷的影响,高超飞行器在飞行过程中需要巨大的推力,从而引起巨大的强噪声载荷,其数量级可达到150 dB到170 dB[7-8]。热声载荷联合作用会使得飞行器壁板造成严重的疲劳破坏。Mei等[8-13]对带有均匀稳态热载荷分布的薄壁结构在随机声载荷作用下的动态响应进行了详细的分析,表明薄壁板在热声载荷作用下会产生复杂的非线性动态响应,其中包括围绕初始平衡位置的非线性随机振动、围绕热屈曲后两个平衡位置的非线性跳变运动以及围绕热后屈曲某一平衡位置的非线性随机振动。但很少资料论述带有温度梯度热载荷的薄板在随机噪声作用下的动态响应。因此,本文选用带有一维线性温度梯度热载荷分布形式的薄板为例,利用有限单元法计算出了定常声压级下带有温度梯度热载荷的四边简支矩形板在热屈曲前后应力动态响应,并对应力响应进行了详细地统计分析(概率密度 PDF、功率谱密度 PSD、有效值RMS)。
1 热声载荷下矩形平板相关理论
结构由于温度变化所引起的热变形受到约束时就会产生热应力。分析温度变化引起的应力、应变,则需要在广义胡克定律中增加温度项。由于下文所研究的结构为薄壁结构,忽略厚度方向温度梯度的影响。因此,可将弹性力学中的应力-应变关系表示为(假设参考温度T ref=0℃)
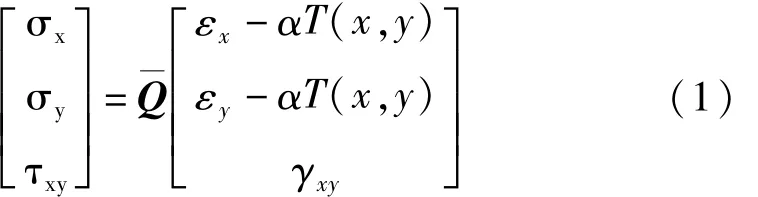
其中,α为热膨胀系数,T(x,y)为薄板温度分布,
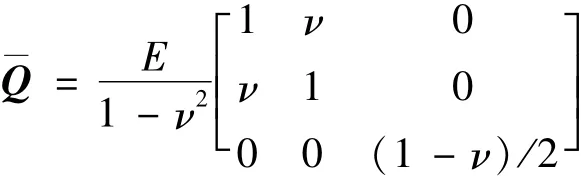
根据直法线假设,距薄板中面距离为z的平面上任意一点的应变可用横向位移w与中面应变分量表示如下
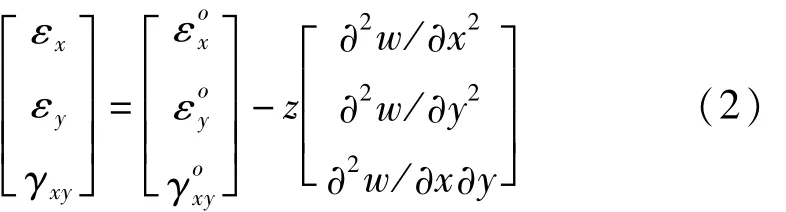
其中,中面应变分量有如下表示

将式(2)作相应微分处理,可以转化为利用中面应变分量与横向位移表示的变形协调方程
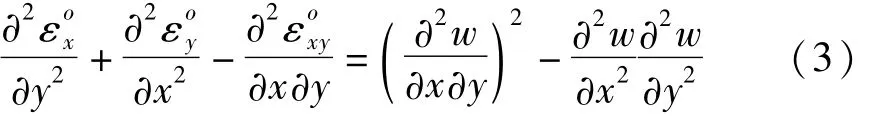
由式(1)的三个应力分量沿薄板厚度方向积分,薄板内力与弯矩有如下形式

将中面应变带入其中,可得到面内力与弯矩的矩阵表达形式
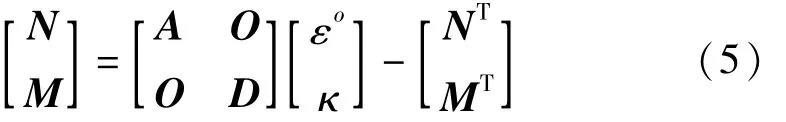
其中,κ表示曲率,NT与MT分别表示热内力与热弯矩。而热内力与热弯矩可用如下方程表示

薄膜矩阵A与弯曲刚度矩阵D表示如下
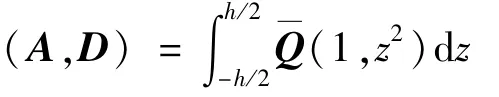
根据M,N及横向位移w可以给出薄板的平衡方程
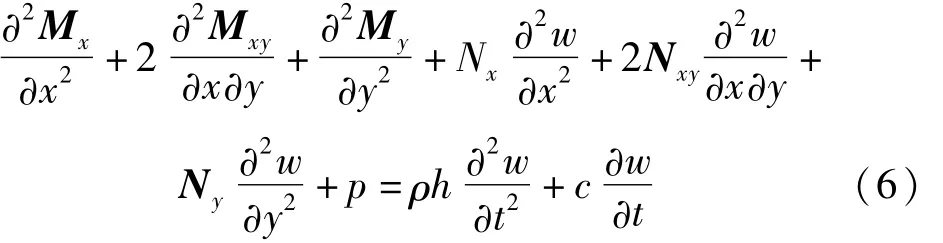
引入应力函数ψ,
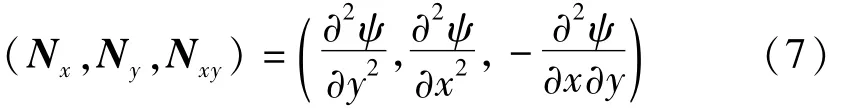
式(7)满足力的平衡方程。将式(7)带入式(6)可得到薄板的大挠度方程如下
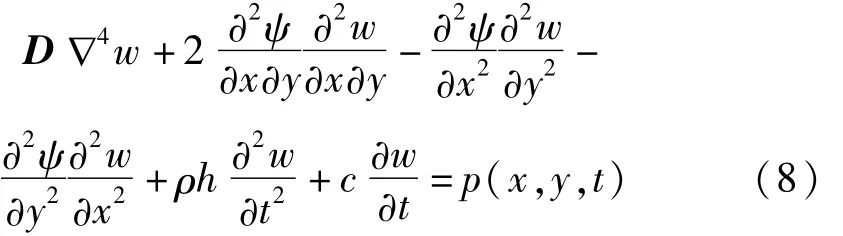
假设四边简支服从不可动边界条件,即四边既无位移又无剪切力,可有如下方程
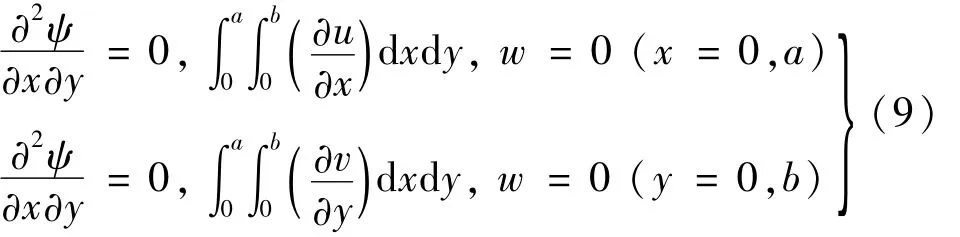
同时,四边简支矩形平板板边界上的弯矩为0,即
根据式(8),结合边界条件,可导出四边简支矩形平板的模态频率计算公式[14]

将式(7)带入式(5),导出利用应力函数所表示的中面应变分量,再带入到变形协调式(3),最后可推出应力函数与位移共同表示的变形协调方程
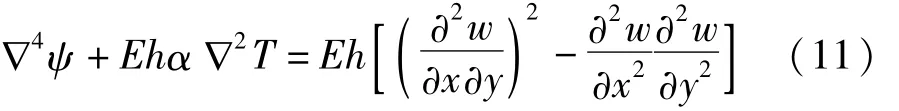
式(8)与式(11)共同构成薄板大挠度控制方程。
若T为均匀稳态温度热载荷,则根据文献[14],通过变形协调方程可导出四边简支板的临界屈曲温度
若仅考虑矩形板平面温度梯度,设左右两边温度分别维持在T1、T2,其物理参数不随温度而变化,并且无内热源,根据稳态传热过程,可将传热学[15]中的三维导热微分方程转化为一维问题,转化后的一维导热微分方程形式如下

边界条件为 T|x=0,T|x=a;对式(13)两次微分可求出矩形平板的线性温度分布如下

式中温度差ΔT=T2-T1.结合文献[6],可导出四边简支矩形板在该温度梯度分布下的临界热屈曲温度差计算公式

式中Tcr为四边简支矩形板在均匀稳态热载荷下的第一阶临界热屈曲温度,由式(12)给出;此时,当 ΔT=Tcru时,四边简支矩形平板发生热屈曲现象。
本文主要采用有限元数值计算方法进行计算求解,因此,根据Hamilton虚功原理,给出薄板热声载荷下的有限元运动方程如下[16]

式中M为质量矩阵;C为阻尼矩阵;K为线性刚度矩阵;KT是由于温度变化引起的热应力刚度矩阵;K1,K2为运动方程的第一阶与第二阶非线性刚度矩阵,且与位移w有关;而f与fT分别表示随机声载荷以及由温度引起的等效热载荷。
在给定边界条件下,式(16)忽略惯性项与随机载荷项,可得到非线性热屈曲方程如下
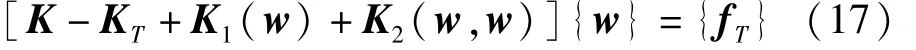
利用Newton-Raphson迭代法对式(17)进行迭代,可以确定指定温度分布下的静态热屈曲挠度{w}s。一旦获得{w}s,可作为初始条件,通过添加惯性项,忽略非线性项,得到关于热屈曲平衡位置{w}s的线性运动方程如下

其中,{w}t表示动态位移,结构总位移响应{w}=t;切线刚度矩阵 Ktan(ws)可在上述 Newton-Raphson迭代法计算中得到[17]。
根据式(18),热屈曲薄板的模态频率ω及振型n可通过下列方程进行求解
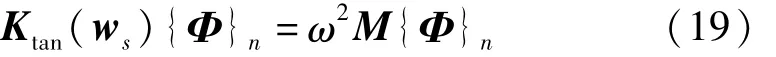
2 数值仿真计算与分析
本文选取四边简支矩形钛合金板作为研究对象,几何尺寸与材料属性如下表1所示。针对温度梯度与声载荷联合作用,采用有限元数值计算方法对其进行了仿真计算,得到了四边简支矩形钛合金板在带有温度梯度的热载荷与声联合作用下的非线性应力动态响应。

表1 几何尺寸与材料属性Tab.1 The dimensions and material properties
根据式(10)与有限元法分别计算出四边简支矩形钛合金板在常温下模态频率的解析解与数值解,如表2所示。利用式(12)以及有限元数值计算方法,计算出了四边简支矩形钛合金板在均匀稳态热载荷下第一阶临界热屈曲温度的解析解与数值解,如表3所示。解析解与数值解经过对比,极为近似,从而可验证数值解的正确性。
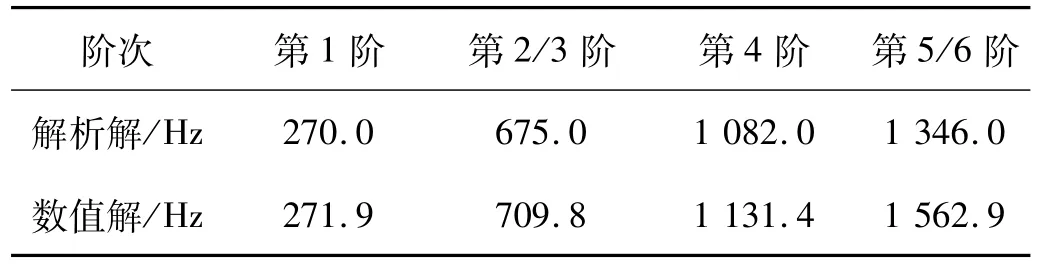
表2 简支板模态频率(无热预应力)Tab.2 Themodal frequencies of simply-supported p late(Hz)(No therm al prestress)

表3 简支板临界热屈曲温度(均温)Tab.3The critical buckling temperature of simply-supported pate(Uniform tem perature)
上述式(14)给出了矩形板在x方向的温度梯度分布,根据式(15)可以求出简支板在该温度梯度热载荷分布下发生热屈曲时的第一阶临界热屈曲温度差Tcru。结合表3中临界热屈曲温度的数值解,利用式(15)可以拟合出该温度梯度热载荷分布下简支板第一阶临界热屈曲温度差随T1的变化规律曲线,如图1所示,从图中发现,随着T1不断增加,临界热屈曲温度差线性递减,直到T1=42.4℃时,临界热屈曲温度差等于0,即简支板在均匀温度42.4℃下,矩形板发生热屈曲失稳,此时,可认为均温导致的失稳为温度梯度作用下的一种特殊情况。
本文以图1中所标注点的位置为例,所研究的温度梯度是以温度差ΔT=30℃为基准,且T1线性变化。可以发现,当T1=27.4℃时,矩形板发生热屈曲现象。为了后文表达方便,可令 S=T1/27.4,即保持 ΔT=30℃,当S=1时,矩形板发生热屈曲失稳现象。本文计算所选取的S范围从0到4,间隔0.2。

图1 临界热屈曲温度差(温度梯度)Fig.1 The critical buckling temperature difference(temperature gradient)
计算得到了不同S(ΔT=30℃)下四边简支板的热预应力模态频率,如下表4所示。结合表2与表4,热屈曲前,温度的升高使模态频率逐渐下降,屈曲后阶段,温度致使简支板基频呈现上升趋势。以S=1(热屈曲时)为例,给出四边简支矩形钛合金板的第一阶Von Mises应力振型云图,如下图2所示。从图中发现,温度梯度导致简支板一弯振动最大Von Mises应力有向温度较高一侧偏移的趋势。
本文所考虑的随机声激励载荷是以总声压级160 dB的限带高斯白噪声,如图3所示。其截止频率为1 500 Hz,且均匀分布在矩形平板上,根据上述模态频率计算,可以覆盖多阶模态频率;载荷信号时长为1 s时的声压时间历程如下图3(a)所示,其声压的概率密度服从正态分布;相应的声压功率谱如下图3(b)所示;
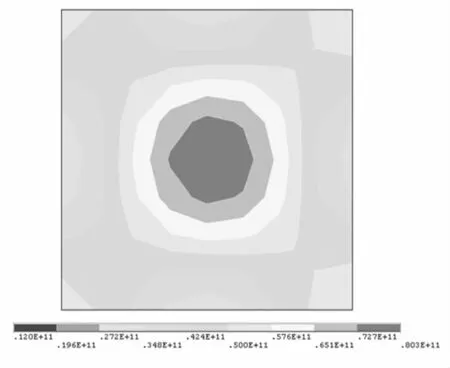
图2 简支板Von Mises应力分布(S=1,ΔT=30℃)Fig.2 Von Mises stress distribution for simple supported plate(S=1,ΔT=30℃)
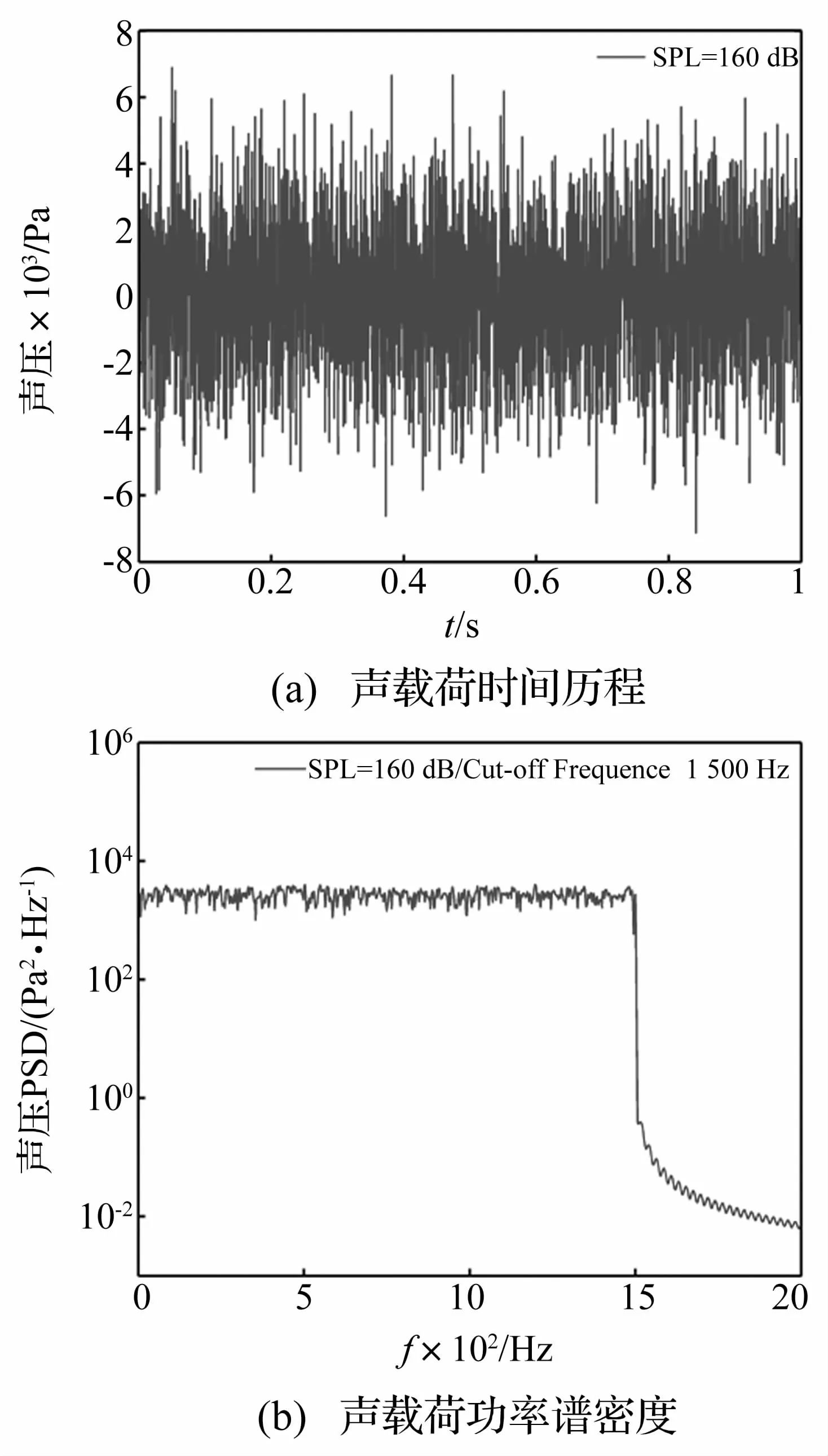
图3 限带高斯白噪声(总声压级160 dB)Fig.3 Band limited white Gauss noise(the overall sound pressure level 160 dB)
2.1 动态应力响应计算与统计分析
本节利用有限元数值计算方法计算了简支板在不同热屈曲系数S(温度梯度不变,ΔT=30℃)、总声压级为160 dB下的应力动态响应。
由于所研究模型为对称模型,且温度梯度分布沿板x向中心线对称,因此,以简支板x向中心线为基准,提取薄板中心线及下侧部分结点进行分析,所要计算的结点位置及编号如下图4所示。

图4 简支板结点编号及位置Fig.4 Node number and position of simple supported plate

表4 简支板模态频率 (ΔT=30℃)Tab.4 Themodal frequencies of sim p ly-supported p late(Hz)(ΔT=30℃)
上图2指出,一弯振动最大Von Mises应力虽然向高温一侧便宜,但偏移量较小,因此,为了说明带有温度梯度热载荷的简支板在随机声载荷作用下的动态特性,以编号为57的中心结点为例,给出其x向应力响应时间历程,如图5所示,相应的概率密度如图6所示。从中可以清晰地揭示薄板在热声载荷作用下的三种运动形式,即屈曲前,薄板围绕初始平衡位置做随机振动;屈曲后薄板的跳变现象以及围绕热后屈曲某一平衡位置做非线性随机振动。
屈曲前,随着温度的增大,应力响应时间历程的对称中心逐渐远离x轴,说明热应力在上升,应力均值绝对值增大,而应力幅值也在增加,如图5(a),图5(b),图5(c)所示。从下述概率密度分布图6(a),图6(b)中可以看出,S=0且ΔT=0℃时,应力均值为0,S=0.6且ΔT=30℃时,应力均值增加到约40 MPa,最大应力幅值大约从20 MPa增加到60 MPa。
图6(a)指出,无热载荷影响时,其概率密度基本服从正态分布。而图6(b),图6(c)表明由于温度的影响,其概率密度不服从正态分布。
在热后屈曲跳变过程中,薄板中点x向应力时间历程处于拉伸与压缩两种状态,如图5(d)所示,拉伸时,应力幅值大于压缩应力幅值,而拉伸应力均值却小于压缩应力均值,这一点在图6(d)概率密度中体现的更加显著。同时,在下述概率密度分布图6(d)中了解到,由于跳变的产生,应力概率密度出现双峰值状态,且不服从正态分布。

图5 简支板中点应力响应 (SPL=160 dB)Fig.5 x component of stress for themidpoint of simple supported plate
图 5(e),图 5(f)指出薄板在 S=1.6,2(ΔT=30℃)时完全处于热后屈曲拉伸阶段的应力时间历程,随着温度的增加,由于热屈曲挠度的作用,拉伸应力均值逐渐增大,但应力振幅却逐渐减小。在下述概率分布图6(e)与图 6(f)中,应力均值约从 60 MPa(S=1.6)增加到大约 128 MPa(S=2),而最大应力幅值约从60 MPa(S=1.6)减小到20 MPa(S=2),并且,在热后屈曲状态,应力概率密度恢复为正态分布。

图6 简支板中点应力概率密度(SPL=160 dB)Fig.6 Probability density for themidpoint of simple supported plate

图7 简支板中点应力功率谱密度(ΔT=30℃)Fig.7 Stress power spectrum density for themidpoint of simple supported plate
对于总声压级为160 dB,热屈曲系数 S=0,0.6,1,1.2,1.6(ΔT=30℃)时薄板中心结点 x向应力的时间历程通过自相关函数计算,然后经过傅里叶变换,可转化为频域下的应力功率谱密度,如下图7所示。由于结构振动基频最为主要,因此,仅考虑基频变化情况。可发现,定常声压级下,屈曲前,随着温度的升高,薄板基频下降;屈曲后,温度升高,导致薄板基频开始上升;这是由于在热屈曲前,薄板随着温度的增加出现软化过程,导致薄板刚度降低;而热屈曲后,温度的增加致使薄板逐渐硬化,导致其基率升高;以上基频变化情况与表2与表4中热屈曲前后基频变化规律基本一致。这种稳定、失稳、再稳定的过程,在文献[9,11]中均温热载荷对矩形平板模态频率的影响论述研究中也有所体现。
本文通过应力有效值(RMS)统计分析,得到了结点57在总声压级160 dB、不同S(ΔT=30℃)下的Von Mises应力有效值(RMS),如图下8所示。
热屈曲前(S=0)直到进入热后屈曲的频繁跳变阶段(S=1.2),简支板应力有效值随着温度的增加而线性递增;从频繁跳变(S=1.2)开始直到跳变结束阶段(S=1.5),由于跳变逐渐减弱致使简支板的应力有效值随着温度的增加呈现下降趋势;而后,应力有效值逐渐上升,此时,简支板围绕热后屈曲某一平衡位置振动,由于随机性,结点57的应力将会出现拉伸或压缩两种状态,这里采用拉伸应力对其有效值进行计算。而由于热屈曲前与热后屈曲跳变阶段,拉伸与压缩应力概率基本相同,计算应力有效值时,可不必对其进行区分。值得说明的一点,简支板在受到热声载荷的联合作用时,存在弯曲拉伸应力、弯曲压缩应力以及压缩热应力。根据不同的温度以及简支板结点位置的不同,三种应力在数值上大小各不相同,因而三种应力相互叠加的结果会出现单纯意义上的拉伸与压缩状态。
考虑到温度梯度(ΔT=30℃)对简支板的影响,结合图4,下面给出了简支板不同位置结点Von Mises应力有效值比较示意图,如下图9所示。图9(b),图9(c)中结点应力在热后屈曲阶会呈现出拉伸或压缩状态,因此,简支板在热后屈曲阶段均采用拉伸应力进行有效值计算。而图9(a),9(d)所对应的结点应力在热屈曲前后均为压缩状态,即为压缩应力有效值。图9(a)与图9(d)中简支板三边中点及角点应力有效值曲线表明,温度较高一侧,其应力有效值相对较大。图9(b)所给出的三点应力有效值经比较发现,中点应力有效值最大,其余对称两结点温度较高一侧应力有效值较大。图9(c)中指出y=0.3×1/8 m处的结点应力有效值,由于温度梯度的存在,在热屈曲前后数值的大小出现交替现象,热屈曲前到跳变结束阶段,温度较高一侧应力有效值较大,热后屈曲围绕上凸平衡位置振动时,温度较低一侧应力有效值较大。
图9指出,简支板上所求得应力有效值的结点中,除了角点1和2以外,其余结点应力有效值随温度的变化趋势基本相同,同时受到频繁跳变、间歇跳变直至跳变结束这段过程的影响,应力有效值在这段过程随温度的增加均出现下降现象。然而,简支板角点1和2的应力有效值在热屈曲前后随着温度的增加却线性递增。图9(a)中三个边界中点均为压缩应力,虽然弯曲压缩应力与压缩热应力的总和大于弯曲拉伸应力,但在跳变过程中,弯曲拉伸应力却在其中占有重要位置。弯曲拉伸应力、弯曲压缩应力以及压缩热应力之间相互作用,导致应力有效值出现下降趋势。角点1、2所处的位置其弯曲拉伸应力远小于压缩热应力,因而压缩热应力致使角点1、2的应力有效值随着温度的增加线性递增。
3 结 论
本文利用有限元数值计算方法对带有温度梯度热载荷的四边简支矩形钛合金板进行热声激振计算,得到结论如下:
(1)根据简支板在线性热梯度作用下的第一阶临界热屈曲温度差计算公式可知,随着简支板低温一侧边界线上温度的增加,临界热屈曲温度差线性降低。
(2)简支板在热屈曲前,随着温度的递增,应力均值增大,应力幅值增加;跳变过程中,应力处于拉伸与压缩两种状态,拉伸应力幅值大于压缩应力幅值,但拉伸应力均值却小于压缩时应力均值;随着温度继续增加,拉伸应力均值逐渐增大,但应力振幅却逐渐减小。
(3)在热屈曲前直到热后屈曲频繁跳变阶段,除角点以外,简支板其余结点应力有效值随着温度的增加而线性递增;从热后屈曲频繁跳变到跳变结束阶段,简支板应力有效值呈下降趋势;温度继续提高,拉伸应力有效值逐渐上升。而角点应力有效值随着温度的增加线性递增。
[1]Ko W L.Thermal buckling analysis of rectangular panels subjected to humped temperature profile heating[R].NASA/TP-2004-212041,2004.
[2]Thornton E A,Kolenski J D,Marino R P.Finite element study of plate buckling induced by spatial temperature gradients[C] //AIAA/ASME/ASCE/AHS/ASC 34th Structures,Structural Dynamics,and Materials Conference.1993,1:2313-2326.
[3]Ko W L.Mechanical and thermal buckling analysis of rectangular sandwich panels under different edge conditions[J]. NASA STI/Recon Technical Report N, 1994,94:33704.
[4]Ko W L.Predictions of thermal buckling strengths of hypersonic aircraft sandwich panels using minimum potential energy and finite elementmethods[M].National Aeronautics and Space Administration,Office of Management,Scientific and Technical Information Program,1995.
[5]Ko W L.Thermostructural behavior of a hypersonic aircraft sandwich panel subjected to heating on one side[M].National Aeronautics and Space Administration,Office of Management,Scientific and Technical Information Program,1997.
[6]Javaheri R,Eslami M R.Thermal buckling of functionally graded plates[J].AIAA Journal,2002,40:162-169.
[7]Dhainaut J M,Guo X,Mei C,et al.Nonlinear random response of panels in an elevated thermal-acoustic environment[J].Journal of Aircraft,2003,40(4):683-691.
[8]Mei C,Dhainaut JM,Duan B,et al.Nonlinear random response of composite panels in an elevated thermal environment[R].Old Dominion Univ Norfolk,VA,2000.
[9]Sha Y D,Li J Y,Gao Z J.Dynamic response of pre/post buckled thin-walled structure under thermo-acoustic loading[J].Applied Mechanics and Materials,2011;80-81:536-541.
[10]Przekop A,Rizzi SA.Dynamic snap-through of thin-walled structures by a reduced-order method[J].AIAA Journal,2007,45(10):2510-2519.
[11]Sha Y D,Gao Z J,Xu F,et al.Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading[J].Advanced Engineering Forum,2011,2-3:876-881.
[12]沙云东,魏静,高志军,等.热声激励下金属薄壁结构的随机疲劳寿命估算[J].振动与冲击,2013,32(10):162-166.SHA Yun-dong,WEI Jing,GAO Zhi-jun,et al.Random fatigue life prediction ofmetallic thin-walled structures under thermo-acoustic excitation[J]. Journal of Vibration and Shock,2013,32(10):162-166.
[13]沙云东,魏静,高志军,等.热声载荷作用下薄壁结构的非线性响应特性[J].航空学报,2013,34(6):1336-1346.SHA Yun-dong,WEI Jing,GAO Zhi-jun,et al.Nonlinear responses characteristics of thin-walled structures under thermo-acoustic loadings[J]. Acta Aeronautica et Astronautica Sinica,2013,34(6):1336-1346.
[14]Sha Y D,Gao Z J,Xu F.Influences of thermal loads on nonlinear response of thin-walled structures in thermo-acoustic environment[J].Applied Mechanics and Materials,2011,105-107:220-226.
[15]杨世铭,陶文铨.传热学(第4版)[M].北京:高等教育出版社,2006.8.
[16]Guo X Y,Przekop A,Mei C,Nonlinear random response of shallow shells at elevated temperatures using finite element modal method[C]. Structural Dynamics& Materials Conference,2004,19-22.
[17]Guo X Y, Lee Y, Mei C, et al. Thermal buckling suppression of supersonic vehicle surface panels using shape memory alloy[J].Journal of Aircraft,2004,41(6):1498-1504.

