U 型变截面薄板面内复合模态驱动的直线超声电机

贺红林，何文丛，刘文光

（南昌航空大学 航空制造工程学院，南昌 330063）

随着航空航天、精密制造等高新技术发展，对小型精密电机要求愈来愈高，需求越来大［1－2］。当前直线电机的实现形式主要有三种：一种是利用钿杆将旋转电机运动转换为直线运动，该类电机结构简单，但受钿杆副间隙及其摩擦影响，其运动精度低、控制性差，特别是其小型化受钿杆尺寸严格限制，故不适于小型精密应用场合；二是由薄型平面绕组及配置于钢尺的单面永磁铁轨道等两部分组成的电磁直线电机，此电机精度较高，但结构复杂、制造困难且平面绕组的小型化同样遇到很大困难；三是直线超声电机（LUSM），这种电机利用压电陶瓷激发超声振动实现电能到机械能转换，直接输出推力和直线运动，定位精度高、结构灵活、便于微型化和轻量化，近年得到快速发展，在小型精密驱动应用中发挥着日益显著作用［1，3］。目前，德、日、美等国的直线超声电机正朝产业化方向发展，在某些高、精、尖领域得到一定的应用［4－6］。国内研究者虽在此领域做了不少工作［7－9］，但总的来讲，国内的 LUSM研究才刚开始，所推出电机原理及型式还极有限，难以满足应用领域提出的更小、更轻、更薄、更短的多样需求，故深入研究LUSM技术基础，推出新原理电机仍是直线超声电机研究的重要方面。据此，作者曾在文献［10］中提出一种H定子驱动的直线电机，该电机结构紧凑、运动精密，适合小型精密驱动，特别是电机实现了两驱动端交替驱动，从而有利于增大动力和速度，但该电机也存在不足：一是电机以定子两斜对角处材料作为驱动端，而对装配提出了很高要求，若装配精度得不到保证，则两驱动端协同驱动难以实现，双端驱动优势也就发挥不出来；二是预压力不便施加和调整；三是驱动端振幅较小。直线超声电机设计的关键一方面是形成驱动端质点椭圆轨迹，另一方面是要增大驱动端振幅以利提高电机速度与动力。为此，从H结构定子得到启发且为发挥该电机之优势并避免其不足，本文提出一种基于U型变截面板面内纵弯模态驱动的直线电机，并规划出电机工作模态，设计出电机装配结构，通过试验验证了电机驱动机理的可行性。

1 电机的原理

1.1 工作模态

本文电机的定子呈U型结构，如图1所示，由两个纵板和一个横板组成，其两纵板小端为驱动端。为避免因加工装配引起纵板与横板连接部出现振动能量损耗，定子采用整体结构。定子设计中，受超声变幅杆原理启发，将纵板驱动端设计成变截面结构，旨在提高驱动端纵向振幅［6］。纵板采用变截面渐缩结构还能降低驱动端弯曲刚度，有利于激发弯曲振动。

图1 预设工作模态Fig．1 Assumed workingmodes

要在驱动端形成质点椭圆运动轨迹，须使驱动端产生空间上正交的两相振动位移［1，7］。根据此要求并结合U板特点，本文选取定子两纵板的二阶对称弯振和一阶反对称纵振模态作为电机工作模态，如图1所示。图中，实线部分表示定子发生振动应变后的状态，虚线表示定子发生振动前的结构。横板既起连接两纵板作用，以利实现两驱动端交替运动，又作定子安装的支承。

1.2 驱动机理

理论上讲，只要在U型定子上适当配置压电陶瓷片（PZT），并在PZT上施以具一定时间相位差的两相等幅同频交流电功率信号，激发定子两相工作模态振动，就能在驱动端形成电机驱动所需质点椭圆运动，再借助驱动端与动子间摩擦作用，就可将定子微幅弹性振动转换为动子直线运动。本文的电机中，纵板二阶弯振的作用是驱使驱动端质点做横向运动、推动动子前行；一阶纵振则实现定子与动子间动态触合与分离。图2给出了在定子一个振动周期（T）内的电机运动情况。

（1）在0～1／4 T期间，左板纵向伸长，驱动端 Y向位移由0增至最大值＋Ymax；同时，左板由内弯状回复成直板状，驱动端X向位移由＋Xmax降至0，致使驱动端质点由A运行到B，推动动子向左移动一个步距λ，如图2（a）。右纵板缩短，驱动端X向位移由0降至－Ymax；同时，右板由内弯状回复成直板状，右驱动端X向位移由0降至－Xmax，使右驱动端质点由F运行到G，右驱动端脱离与动子接触。

（2）在1／4 T～1／2 T期间，左板回缩，其驱动端 Y向由最大值＋Ymax降至0；同时左板弯曲成外弯状而使驱动端X向位移由0降至－Xmax，从而使驱动端质点由B运行到C，推动动子再移进一个步距λ。右板伸长，使右驱动端Y向位移由－Ymax增至0，且右板由直板状弯曲成外弯状而使右驱动端的X向位移由0增至＋Xmax，而使右驱动端质点由G运行到H，保证驱动端不与动子接触。

（3）在1／2 T～3／4 T期间，左板缩至最短，其驱动端Y向位移由0降至－Ymax；同时，左板由外弯状回复成直板状，使驱动端X向位移由－Xmax增至 0，致使质点由C行至D，从而使右驱动端与动子脱离。右板伸长使右驱动端Y向位移由0增至Ymax；右板由外弯状回复成直板状，使右驱动端X向位移由＋Xmax降至0，从而使右驱动端质点由H运行到I，推动动子向左移进第3个步距λ。

图2 定子在一个振动周期内的运动Fig．2 Driving principle of themotor

（4）在3／4 T～T时，左板伸长，左驱动端Y向位移由－Ymax增至0；左板由直板状弯成内弯态，使驱动端X向位移由0增至＋Xmax，使驱动端质点由D运行至E，旨在保持右驱动端不与动子接触。同时，右板回缩，右驱动端Y向位移由Ymax降至0；右板由直板状弯曲成内弯状，使右驱动端X向位移由0降至－Xmax，从而使右驱动端质点由I运行到J，并推动动子再向左移进第4步距λ。

定子每完成一个振动周期，其两驱动端上质点便各完成一次正向椭圆运动，实现动子的一次驱动并推动动子前移4λ。若逆换两相振动的时间相位关系，驱动端质点将做反向椭圆运动，从而推动动子作反向直线运动。

1．3 驱动端运动的描述

U型薄板动力学条件较复杂，对其进行振动分析时，很难求得精确解析解。但若只定性分析其两纵板工作模态振动，却可将其纵板简化为 Bernoulli-Euler梁。考虑到在同一振动周期内，两纵板交替对动子进行驱动，它们的运动情况完全相同，因此为图简便，可只取一个纵板（如左板）进行分析。

对于做纵弯复合振动的纵向板，根据振动理论，不难建立其动力平衡方程并推得其二阶弯振和一阶纵振的振型函数

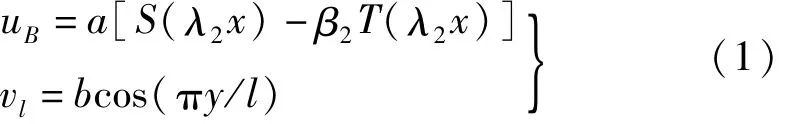
式中，a、b分别表示弯振、纵振的相对振幅；l为纵板振动方向定子长度；S、T均为Krylov函数。

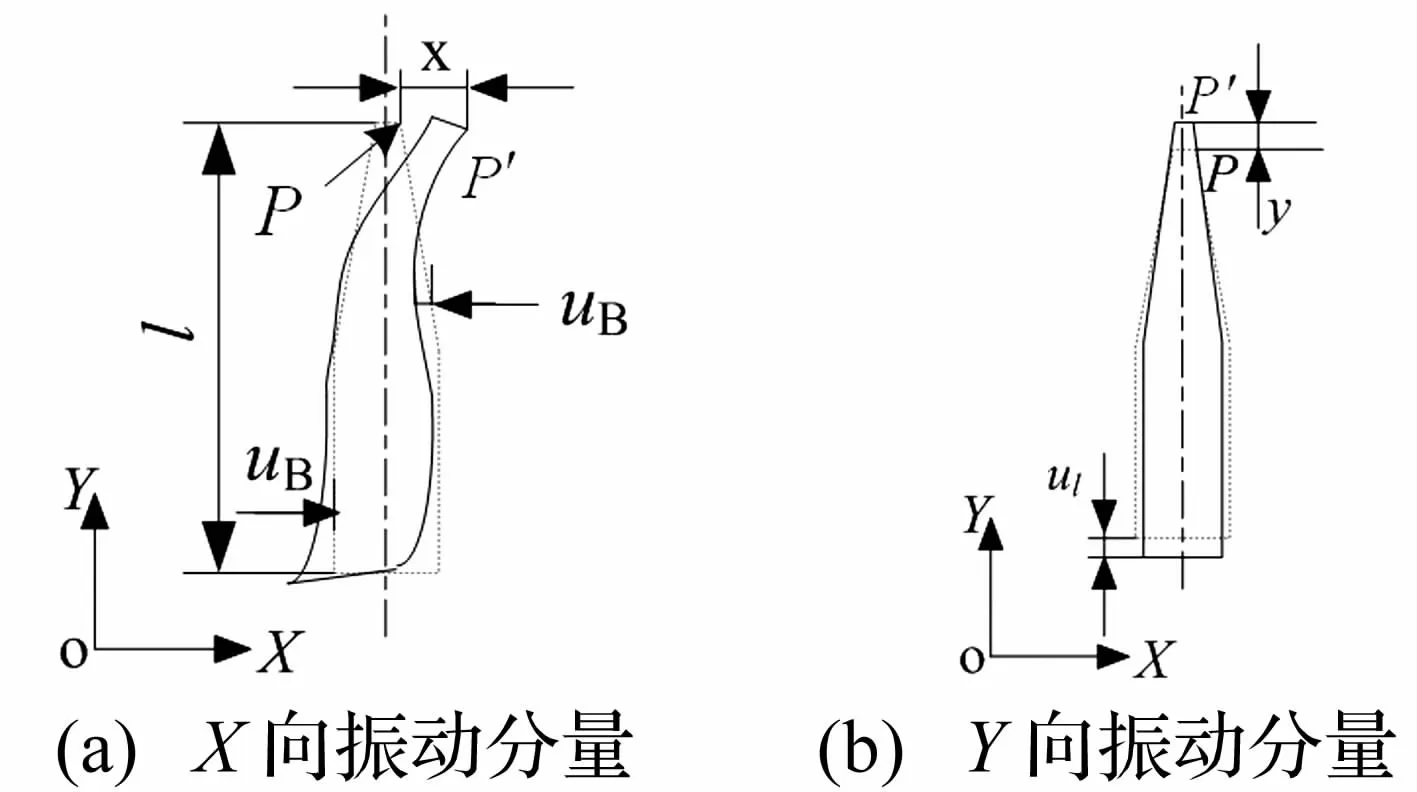
图3 驱动端质点振动位移描述Fig．3 Movement of the particle on drive end

纵板同时作弯振和纵振时，其驱动端呈现图3所示运动状态。可见，当定子两相工作模态被激发时，纵板的伸缩与弯曲导致驱动端质点由P移至P′，从而使质点产生横向位移x和纵向位移y。驱动端质点的响应函数分别为

式中，ω为驱动信号圆频率；α、β为弯、纵振初始时间相位。uB、vl分别表示质点的X、Y向振幅。式（2）中消去时间变量后，得驱动端质点轨迹

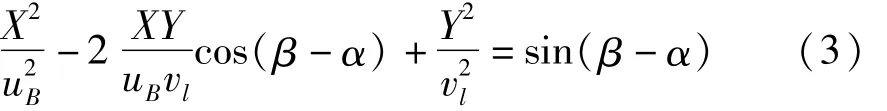
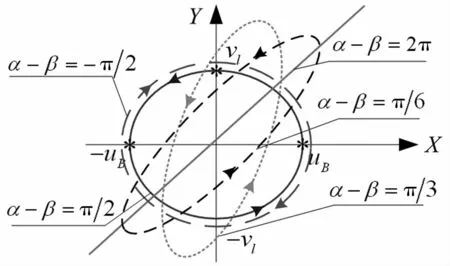
图4 驱动端质点轨迹与两相振动相位差间关系Fig．4Drive end’s trajectory versus the phase difference between the vibrations based on work modes

显然，当时，上式简化为

此时，驱动端质点的运动轨迹退化为一条斜率为±vB／ul的斜直线。

当｜α－β｜＝π／2时，质点的运动轨迹为标准椭圆

图4给出了纵、弯振相位差不同时，驱动端质点的运动变化情况，它表明，当两相模态振动相位差在（0，π／2］内时，驱动端质点做正向椭圆运动；当相位差为［－π／2，0）时，质点将做反向椭圆运动。

1．4 振幅的放大

前文述及，为增大驱动端纵向振幅，定子驱动端设计成线性变截面。为此，有必要对变截面引起的纵振放大效应进行分析。如图5，根据结构振动理论，当纵板发生纵振时，纵板内的纵向波动描述为

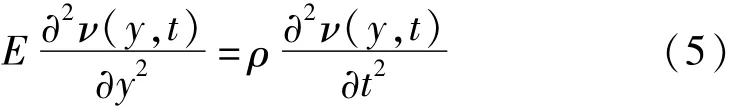
其中，v表示该板x处质点的位移，E为弹性模量，ρ是纵板的密度。根据上式，可推导出变截面纵板的质点振动方程为［7］

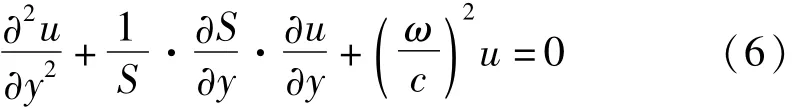
式中，S＝h·x（y）为纵板驱动端截面积函数。将S代入得式（6），可得

图5 线性变截面结构示意Fig．5 Solid horn’s vibration amplification effect

当且仅当变截面轮廓为抛物线或指数曲线时式（7）才有封闭解。因此，为图简便，且不失一般性，可直接假设截面轮廓为抛物线，并令

式中将式（8）代入式（7），则得到

可见，当随着质点纵向位置x增大，其振幅v也相应增大，说明变截面纵板具有放大振幅的功能。但纵板驱动端横向尺寸也不宜过小，否则会影响电机功率输出。可见，在确定变截面尺寸时，必须在振幅放大和功率输出方面进行权衡。

2 定子构型及压电配置

图6给出了定子构形及其压电陶瓷极化供电配置。根据轻量化要求，定子采用贴片式压电陶瓷进行激励，并基于PZT的d31效应诱发振动。根据超声换能器理论，要激发出尽可能大的纵振振幅，宜将PZT配置在定子最大纵向应变处。为此，分别在定子纵振工作模态节线附近以及弯振模态波峰和波谷处粘贴压电陶瓷片。图中粘贴于纵板变截面驱动端两侧的压电陶瓷片是用来激发弯振工作模态，其余4片PZT则激励纵振工作模态。本文之所以配置了较多纵振PZT片，主要是为增大定子激振力，以提高电机动力输出。驱动端附近开设小孔是为了修正模态。

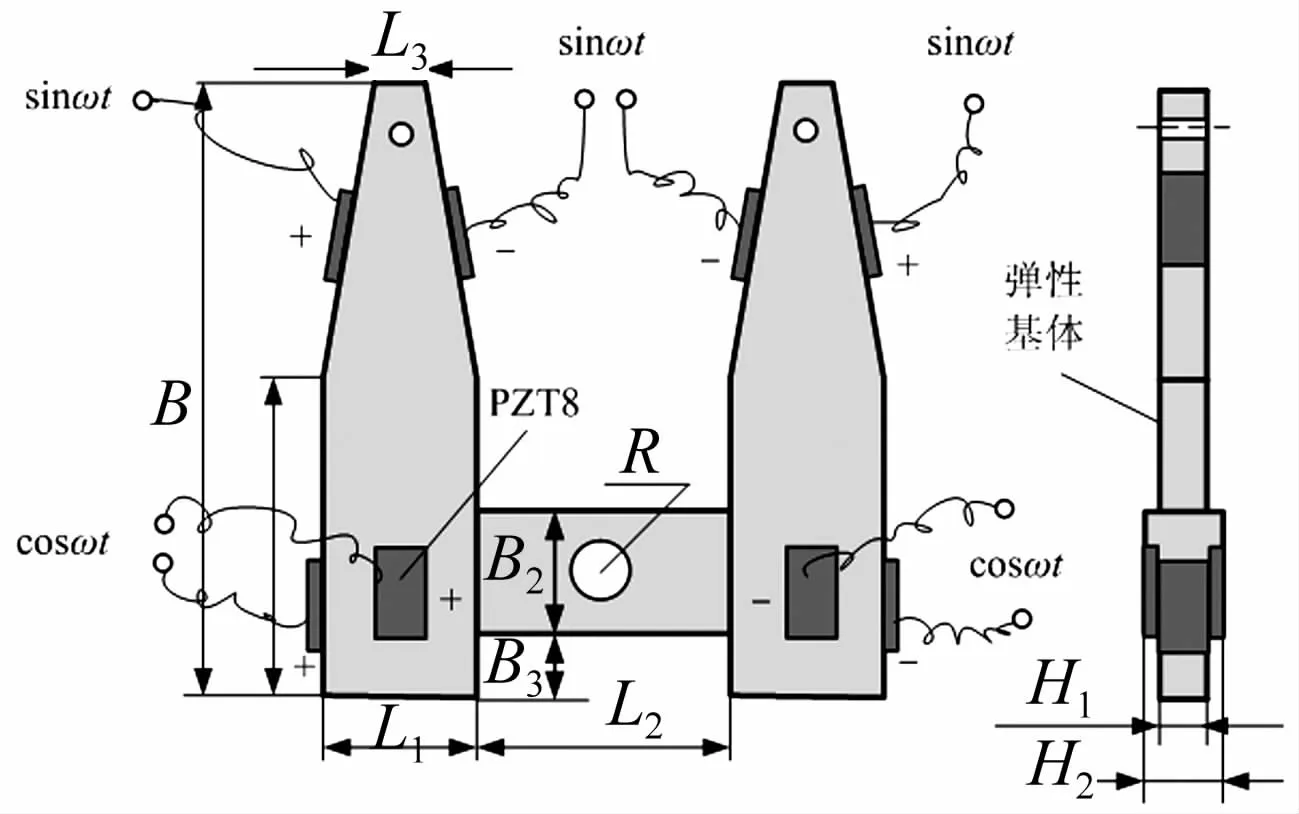
图6 定子构型及其压电配置与供电Fig．6 The structure of the stator

定子设计初期，根据经验并借鉴文献［10］，初定了定子结构及其尺寸，但在随后的定子数值计算中发现：若定子纵板与横板厚度取相同值，则定子工作振型非常差；但当将它们的厚度设计成不同尺寸时，则能改善工作振型。据此并考虑定子的安装及其自由边界条件实现等问题，最后将纵、横板厚分别设定为H1＝2 mm和H2＝3 mm。定子其它尺寸的初值列于表1中。

表1 定子结构的初始尺寸Tab．1 Theinitial size of the stator

3 定子结构动力学分析

3.1 分析模型

前文在模态假设的基础上阐释了电机的机理，但定子是否存在该模态，尚需通过结构动力学分析予以确认。根据薄板理论，对于形状简单的矩形板和圆板，采用解析法可精确求解结构的振型与固有频率，但对于U型板这样的异形结构，解析法是无能为力的，故本文只能借助数值法求解U型板的振动参数，并采用An-sys对定子进行结构动力学分析。

U型定子的电激弹性谐振，涉及到复杂的结构、力场、电场的耦合问题。用数值法求解其振动特征量时，须先将定子的弹性基体及其压电陶瓷离散成多个结构单元，需在各单元设置若干节点且要在各节点定义位移自由度。对于压电陶瓷单元，还要为节点定义电势自由度，并引入压电本构方程以描述单元的力电耦合关系。这样，便可得定子有限元动力学方程

式中，［Mm］、［Km］分别为弹性基体单元质量阵和刚度阵；［Kme］、［Ke］分别表示压电单元的压电耦合阵和介电矩阵；｛F｝为定子与动子在接触面上的广义作用力；为压电单元电极上的电荷；［δ］为节点位移向量；［qe］为节点电荷自由度向量。

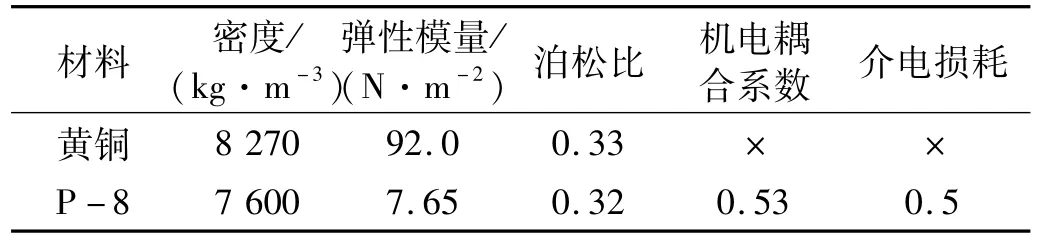
表2 定子有限元分析的部分材料特性参数设定Tab．2 M aterials property model for the stator

采用ANSYS对方程（10）进行求解时，定子弹性基体采用八节点六面体单元Solid45进行网格划分，压电陶瓷则采用Solid5机电耦合单元实现网格化，并且根据电机驱动机理，为定子设定自由边界条件。材料设置方面，压电陶瓷选PZT8（15 mm×5 mm×1 mm），定子弹性体采用黄铜。定子计算时，设定的材料性能参数，如表2。图7给出了定子有限元建模及其工作模态求解结果。

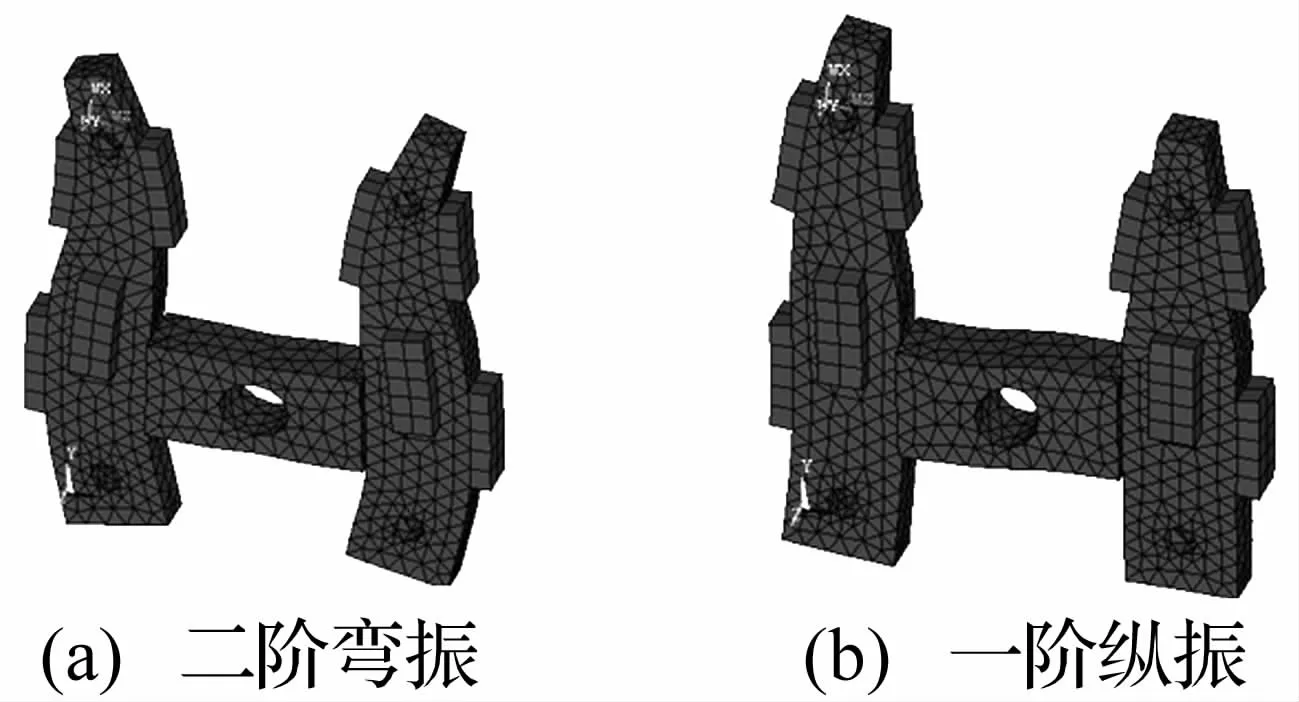
图7 纵弯模态振型的数值计算结果Fig．7 Caculated work modes of themotor

3.2 尺寸优化

为保证驱动端质点作椭圆运动，定子两相工作模态应尽可能纯正且两相工作模态频率趋于一致，这有赖于定子结构尺寸优化。而要找到满足频率一致性的尺寸，并保证电机微型化、轻量化、大振幅，则需针对定子尺寸作模态灵敏度分析。事实上，该分析不仅是电机设计基础，也是定子模态修正及电机调试的依据。考虑到前文计算已表明：只当纵板与横板间有厚度差时，才能激发出纯正工作模态，因此，灵敏度分析时将H1和H2尺寸固定。同时，根据驱动端结构及电机装配要求，设定驱动端宽L3、横板尺寸L2×B2及安装孔径R为定值。考虑到PZT不便作为优化变量，因此在优化时，主要对未粘贴PZT的弹性基体进行计算，得到优化尺寸。进而对粘贴了PZT定子进行模态修正，得到最终尺寸。定子频率一致性优化模型的形式化表示为

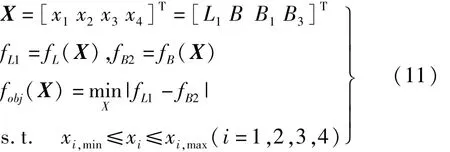
式中，fL1、fB2分别表示定子一阶纵振和二阶弯振模态频率；fobj为优化目标函数；xi，min，xi，max分别表示各相关结构尺寸的最小值和最大值。

图8 定子尺寸对模态频率一致性的影响Fig．8 Modal frequency versus the size of the stator

上述模态频率一致的定子优化模型是一个多变量优化问题。求解该模型时，针对待优化变量，取定较小迭代步长，并利用Ansys逐一计算出变量迭代后的定子工作振形及模态频率，从而寻得设计变量最佳值。图8给出了计算所得的定子模态频率灵敏度曲线。图（a）表明，增大纵板大端宽L1，纵、弯模态频率增大且当L1为5 mm时，两相模态频率相等；在图（b）中，增大纵板定截端长度B1，则纵振频率递增而弯振频率先增后降，且在B1为12．5 mm时，纵、弯频率曲线最接近；图（c）中，当纵板长B小于24．5 mm时，频率一致性均较好，但当B为24 mm时，频率一致性最佳。图（d）为纵板大端长度B3的影响，当B3增大时，弯振曲线先增升、后变平坦，纵振频率则持续增大，两典线在B3为5．5 mm处交汇。根据计算，得到弹性基体的优化尺寸如表2。按该组尺寸制作的定子，既具较好的模态振型，又可使两相工作模态频差控制在较小范围内。分析还表明，对于已制成定子，若模态频率严重不一致，在模态修正时，可优先选取纵板大端长作为修正尺寸。

经尺寸优化的定子弹性基体，在粘贴了PZT后，其两相模态频差会增大且有f弯＞f纵，故还需对频率一致性进行微调。为尽量减小对工作模型振型产生影响，本文通过在弯振节线处开小孔来降低了弯振频率。计算表明，当孔径为1．5 mm时，纵弯模态频率差最小且模态较纯正。图7给出的即是定子的理论计算模态。可见，该模态与图1所示假设工作模态大体上是一致的。

3．3 谐响应分析

若定子在正常激励下所产生的振幅过小，电机将无法正常运行；同时，若工作模态附近存在多个振幅与工作模态相近的干扰模态，电机效率将严重下降。因此，在对定子进行结构动力学分析时，不仅要考虑频率一致性问题，还需研究其谐响应特征。据此，本文用数值解法求取定子的频响函数，图9给出了定子纵、弯两相振动频响曲线，谐响应分析时的频段设定在70～80 kHz，可见定子的纵、弯振工作模态频率分别为76 379 Hz和76 588 Hz，二者相差甚小，频率一致较理想。进而，本文对上述工作模态进行定频计算，求得定子在200 V激励时的弯振振幅为10．92μm，纵向振幅为11．26μm。两相振动的振幅很接近，这表明定子处于近共振态时，足可产生电机驱动所需振幅，也说明电机能在速度和动力输出上得到较好的平衡。

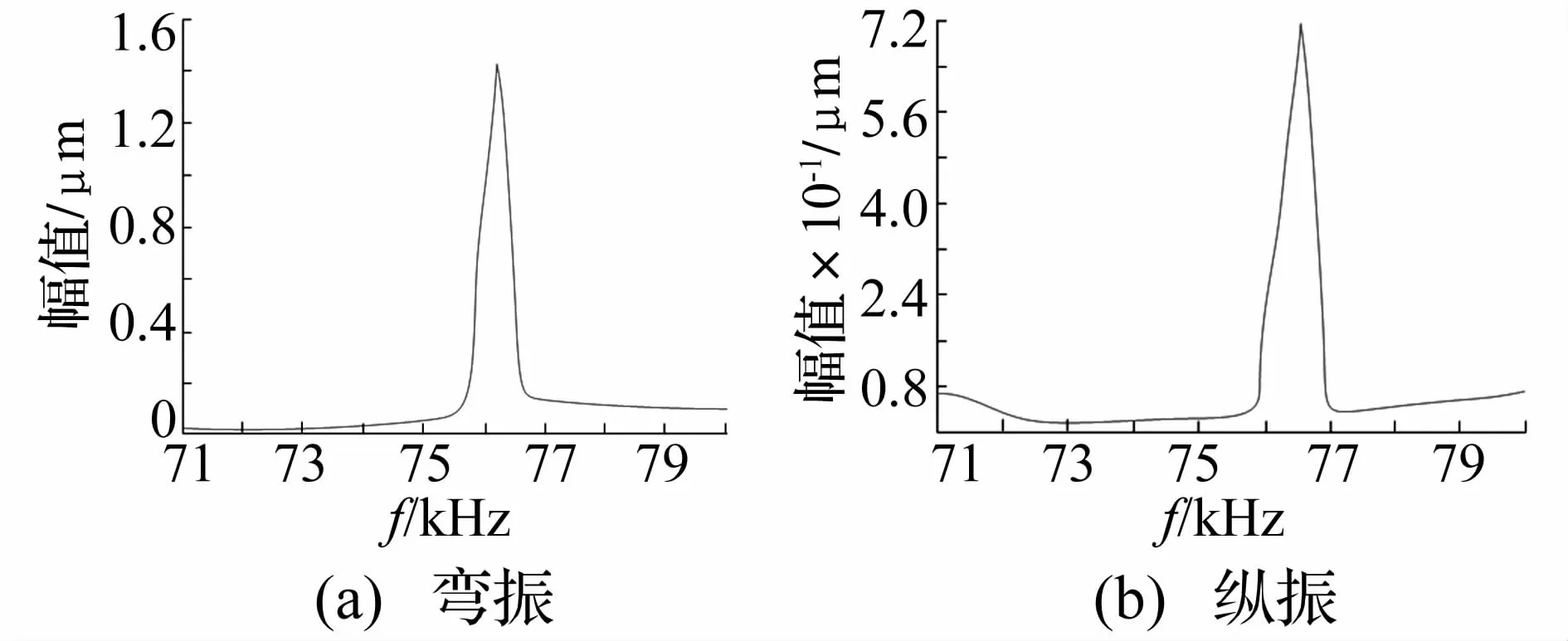
图9 定子的理论计算频响特性曲线Fig．9 Frequency harmonic response property

4 样机实验

4．1 扫频试验

为进一步验证电机的工作模态的存在性，本文制作出定子的原型结构，并利用德国产Polytec激光多普勒测振仪PSV－300F－B对定子分别进行了扫频和定频试验。图10给出了定子扫频结果，可见，纵振工作模态附近很宽的区域内不存在干扰模态。而在弯振频响图中，虽然呈现出一弯和二弯等两个模态，但二者频率相隔较大。这就说明，该电机工作时，干扰模态的影响将非常小。

图10 利用激光测振仪测出的定子频响曲线Fig．10 Frequency sweeping results

表3列出了工作模态频率计算值与实验结果的对比。不难看出，实测值与计算值存在一定偏差，分析其原因可能是由于：① PZT实际粘贴位置与理论位置相差较大：1．3 mm，计算表明该误差将引起弯振大幅降低而纵振略有提高，同时PZT切割过程出现尺寸变化，也引起模态频率变化。② 用ANSYS计算模态时，对定子做了较大简化，忽略定子结构阻尼，且对定子边界做了自由假定，这是造成计算与实验结果不一致的又一原因；③ 实验中用螺钉固定定子，螺钉的尺寸、质量、刚度、阻尼等也给模态频率带来一定影响，特别是定子用螺钉固定后，其刚度有所提高，造成纵弯频率均增大；④ 定子加工装配误差对模态频率产生影响。可见，加工后定子出现频率变化也属正常。本文通过调节弯振节点位置钻4个小孔而对模态频率进行了调节。

表3 模态频率的数值计算与扫频实验结果Tab．3 Modalfrequency from calculation and experiment

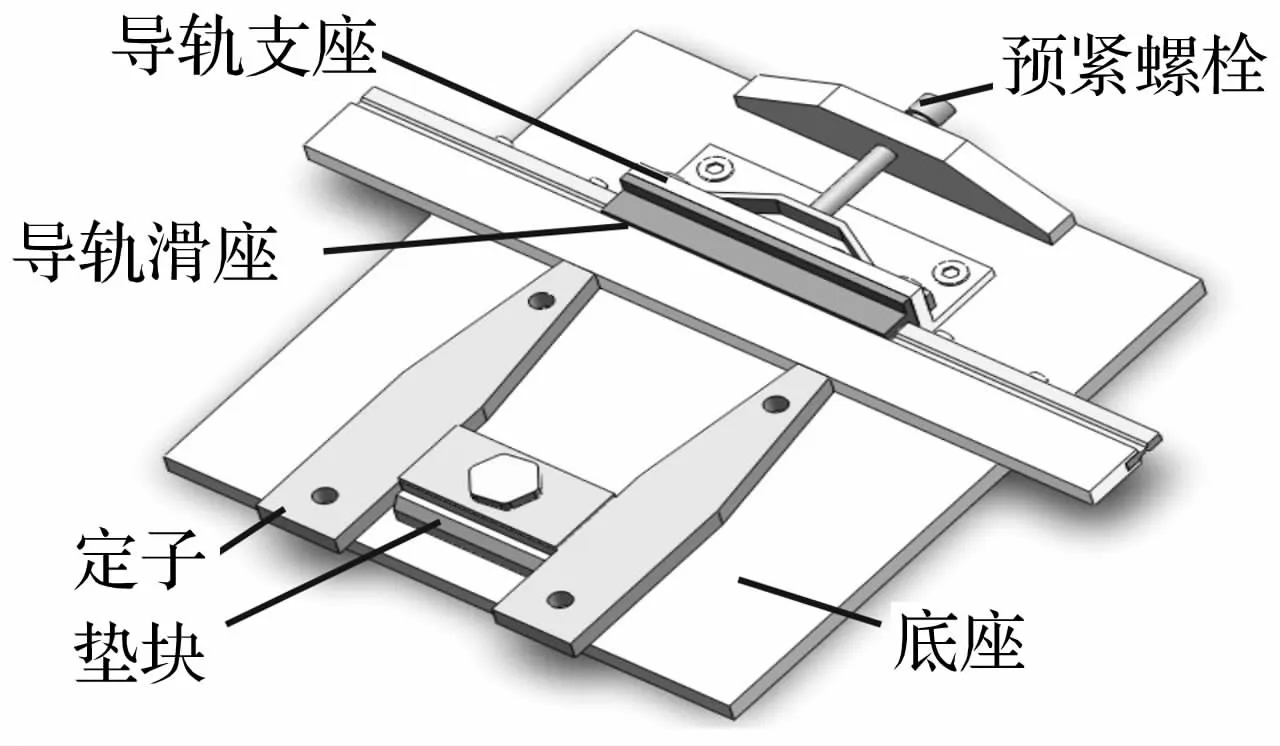
图11 电机装配结构Fig．11 Assemble structure of themotor

4．2 装配方案

图11给出了电机的装配方案，该电机由定子、底座、定子支座和预紧加压机构等四部分组成。在电机底座的一端安装动子滑座，动子导轨在驱动力作用下沿滑座做往复直线运动。为保证定子在振动时不宜与底座接触，在支座夹持处设置一个与底座固连的槽型垫块，这样就使定子悬空于底座固定在支座上，并且限制其在工作平面的转动。同时从支座后方采用调节螺钉对定子施加预压力并使其与动子保持良好接触。

4．3 运行试验

为验证电机原理及特性，搭建出电机驱动控制系统，如图12，该系统主要由信号发器（AFG3022B）、容性负载高压功率放大器（HFPA－42）和电机组成。图（a）给出了试验原理，图中信号发生器输出的两路等幅同频且相位差可调的简谐信号，经功率放大后施加于定子PZT以激发工作模态，驱动电机运转。图（b）给出了定子实物结构及其电路接线。为检验电机原理，将电机装配方案中的直线导轨改换滚动轴承。试验表明：系统通电后，滚动轴承迅速启动且能长时间稳定运转；更换另一驱动端对轴承进行驱动时，轴承以几乎相同的转速同向稳定运转。但若将输入了电机的两相电信号进行对调，即逆转两相模态激励信号超前、滞后关系时，滚动轴承则反转。这与预期结果相吻合，表明本文提出的电机原理完全可行。

图12 直线超声电机速度特性测试平台Fig．12 Experiment system formotor running

基于上述驱制平台，通过调节信号发生器输出频率以及调节功放增益，并采用手持速度表进行测速，本文测得了该电机的调频速度曲线如图13和调压速度特性，如图14。在进行调频速度特性实验时发现，当驱动信号频率处在77．6 kHz到78．4 kHz之内时，电机运转性能良好，特别是在频率为78．11 kHz时，出现了速度峰值，但电机速度与驱动速率间不存在线性关系。从调压速度曲线可见，在一定范围内增大驱动电压幅值，电机速度增大且它们存在一定线性关系。特别是，当两相驱动信号相位差为90°，频率为78．1 kHz，电压幅值为240 V时，电机的最大速度达125．6 mm／s。

图13 直线电机调频速度特性Fig．13 Motor’s speed versus driving frequency

图14 直线电机调压速度特性Fig．14 Speed versus the amplitude of driving voltage

5 结 论

（1）提出一种基于U型变截面薄板面内复合模态驱动的直线超声电机。电机选定U板两纵向板一阶反对称纵振和二阶对称弯振模态作为工作模态。

（2）建立了定子纵振、弯振工作模态频率一致性优化模型，优化出定子结构尺寸。

（3）制作出电机原理性样机，通过定频与扫频实验，验证了电机工作模态的存在及其纯正性。

（4）构建电机驱动控制平台对电机进行驱动控制，验证了电机机理的可行性及其运转的稳定性。

（5）通过调节驱动电压的频率及幅值，可改变电机的速度。当驱动的电压峰－峰值为240 V，且驱动频率为 78．1 kHz，电机无负载最大速度达 125．6 mm／s。

［1］Zhao Chun-sheng． Ultrasonic motors technologies and applications［M］．Beijing：Science Press，2010．

［2］Yao Zhi-yuan， Zhao Chun-sheng，Zeng Jin-song，et al．Analytical solution on the non-linear vibration of a traveling wave ultrasonic motor［J］Journal of Electroceramics，2008，20（3－4）：251－258．

［3］Lee Won-hee， Kang Chng-yun， Paik Dong-soo，et al．Butterfly-shaped ultra slim piezoelectric ultrasonic linear motor［J］．Sensors＆Actuators A：Physical，2011，168（1）：127－130．

［4］Roh Y，Kwon J．Development of a new standing wave-type ultrasonic linear motor［J］．Sensors and Actuators A：Physical，2004，112（2－3）：196－202．

［5］Saigoh H， Kawasaki M，Maruko N，et al． Multilayer piezoelectric motor using the first longitudinal and the second bending vibrations［J］． Japanese． Journal of Applied physics．1995，34（5B）：2760－2764．

［6］ Vyshnevskyy O，Kovalev S，Wischnewskiy W．A novel，single-mode piezoceramic plate actuator for ultrasonic linear motors［J］．IEEE Transactions on Ultrasonic，Ferroelectrics，and Frequency Control，2005，52（11）：2047－2053．

［7］姚志远，赵姝淳，江超，等．扇形直线超声电机的结构设计［J］．振动、测试与诊断，．2013，33（1）：40－43．YAO Zhi-yuan，ZHAOMei-chun，JIANG Chao，etal．Design of a fan-shaped ultrasonic motor［J］．Journal of Vibration，Measurement＆Diagnosis，2013，33（1）：40－43．

［8］张建滔，李朝东，何晓菁．卧板式直线超声电机的特性分析模型［J］．中国电机工程学报，2012，32（18）：137－144．ZHANG Jian-tao，LIChao-dong，HE Xiao-jin．Modeling for characteristic of a plate-type ultrasonic motor［J］．Proc．of the CSEE，2012，32（18）：137－144．

［9］陈乾伟，时运来，黄卫清．新型塔形直线超声电机［J］．中国电机工程学报［J］，2010，30（36）：27－32．CHEN Qian-wei，SHIYun-lai，HUANG Wei-qing．A novel tower-shaped linear ultrasonic motor［J］．Proc．Of the CSEE，2010，30（36）：27－32．

［10］贺红林，武冬梅，何文丛，等．H－结构薄板纵弯复合模态驱动的压电直线电机［J］．振动与冲击，2013，32（5）：1－5．HE Hong-lin， WU Dong-mei， HE Wen-cong，et al．Ultrasonic linearmotor driven by the longitudinal and bending vibration modes of an H-shaped vibrator［J］．Journal of Vibration and Shock，2013，32（5）：1－5．