基于交互密度算子的交互式群体评价信息集结方法及其应用

张发明

（南昌大学经济与管理学院,江西南昌 330031）

基于交互密度算子的交互式群体评价信息集结方法及其应用

张发明

（南昌大学经济与管理学院,江西南昌 330031）

交互式群体评价的一个难点问题是评价信息的集结问题,而国内较少有文献从信息集结算子的角度进行探讨,针对这种不足,同时考虑到信息分布密度是交互式群体评价信息集结的一个重要特征,本文提出了一种基于交互密度算子的交互式群体评价信息集结方法。提出了交互密度算术加权算子（IDWA）与交互密度几何加权算子（IDWGA）两种新的算子,并对新算子的相关性质进行了分析,同时介绍了IDWA和IDWGA算子加权向量（即密度权向量）的确定方法。最后将该方法进行了运用。文章对交互式评价信息集结问题提供了一种新的研究思路。

群体评价；IDWA算子；IDWGA算子；信息集结

1 引言

交互式群体评价因其能够借助群体智能实现评价问题的科学化、系统化、民主化排序而成为近年来评价与决策理论领域研究的新焦点。现有该类研究的基本思路是以成员交互为手段逐步挖掘评价信息,并在此基础上应用模糊优化等求解技术实现对方案的排序择优[1-3,16］。如Xiong Jian[4］从多目标规划的角度对群体交互信息进行集结与求解；文献[5-9］提出了基于不完全信息的交互式群决策方法；Chun等[10］和Xu Zeshui[11］从模糊语言的角度探讨了交互式群体评价信息集结方法；Sun Xiaoyan等[12］利用遗传算法对群决策问题进行求解并对交互信息进行进行集结；Koksalan等[13］构建了一种适用于可加性效用函数的多属性决策方案交互式分类方法；陈建中等[14］基于定性评价排序信息研究了交互式TOPSIS群决策方法,等等。上述成果大多属于假设评价或决策系统为线性理性的决策模式,而该模式在现实决策中会经常出现信息合成谬误等问题[15］,杜元伟[16］基于和谐思想对该问题进行了改进研究,分别从最小化认知分歧和最大化系统和则度的技术视角探讨了一种基于和谐思想的交互式多属性群决策信息集结方法。上述文献均直接或间接地反映了一个问题,即对于整个交互式群体评价问题而言,信息集结是其中的一个关键而复杂的问题,它具有以下几个难点：（1）如何对多阶段动态特征信息进行集结；（2）如何将群体的大规模信息进行集结；（3）如何在信息集结时考虑评价信息的交互性特征,以体现交互式评价特点。然而,现有文献较少有从信息集结算子的角度进行考虑[14］,基于这种不足,并考虑到信息分布是复杂的交互式评价信息的一个主要特征,本文探讨了一种新的信息集结算子——交互密度信息集结（IDA）算子。利用IDA算子对交互式群体评价信息进行集结能够较好地反映评价信息的分布特征,对解决交互式群体评价信息集结的难点问题提供了一种可供借鉴的思路。

2 交互密度信息集结算子

设有m个评价者对n个被评价对象进行评价,被评价对象集为X=｛x1,x2,…,xn｝,评价群体集为S=｛s1,s2,…,sm｝,评价群体与n个评价对象均有一定的利益相关关系,为了平衡各方的利益,假设共经过l（l≥3）轮交互,其交互过程主要表现为：评价个体si（i=1,2,…,m）在第t（t=1,2,…,l）轮交互中参考“公告板”（主持人在每轮交互结束时公布信息的平台）上的信息,对自己上一轮所给出的信息进行修正,并给出该轮交互中的意见,该过程的实质是评价群体成员之间意见的非“面对面”形式交互,在每一轮交互反馈过程中,群体信息必将影响到个体的行为,且通过这种多阶段的交互调整,群体最终的意见将趋于稳定或一致。xii（tk）表示在第tk（k =1,2,…,l）轮交互中si（i=1,2,…,m）对被评价对象xi（i=1,2,…,n）重要程度的评分值（假设不论效益型或成本型属性均以专家打分值的大小来衡量方案的优劣,属性值越大方案越优,且其评分取值区间为[0,10］,特别地,xii（t0）表示最初未经过交互的原始评价信息）,这样一组按时间顺序排放的平面数据表就构成了一个群体时序评价数据表（不失一般性,设n≥3,且m≥3）,记N=｛1,2,…,n｝, M=｛1,2,…,m｝,L=｛1,2,…,l｝,R=｛1,2,…, r｝。

表1 群体交互评价数据表

由于面对同样的问题从不同角度各人的观点是有差别的,但不存在根本的利益冲突,因而对各方观点的“交互集成”成为该问题的主要特征,本文正是基于该种思想,并融合了群体信息的“密度”特征,从交互密度信息集结算子的角度尝试探讨,以期开发出一种能够较好地集结交互评价信息的群体评价方法。

2.1 交互密度加权集结算子

在交互式群体评价中,由于交互信息是多专家、多阶段评价信息,因此交互信息集结是一个复杂的问题,基于此本文提出了交互密度信息集结算子的概念。在交互信息集结中,设v为“交互特征”诱导分量,用于反映交互信息集结的特征,如“一致性”交互特征或“稳定性”交互特征等；x为数据分量,表示被评价对象xi（i=1,2,…,n）在交互中的评价数据信息,则称〈v,x〉为x的交互信息数据对.设n个交互信息数据对组成的交互数据对组为A=｛〈v1,x1〉,〈v2,x2〉,…,〈vn,xn〉｝,A1,A2,…,Ar为A经聚类分组后的r个非空子集合,且具有以下两个特征：（1）Ai∩Ai=∅,i≠i i,i=1,2,…,r；（2）A1∪A2∪…∪Ar=A。同时,设第Ai（i=1, 2,…,r）中数据元素个数为ki（1≤ki≤n-r+1）,∑ki=n。

定义1： 设〈vi,xi〉（i=1,2,…,n）为IDWA对,称IDWA算子为交互密度算术加权集结算子,其表达式为：

定义2：设〈vi,xi〉（i=1,2,…,n）为IDWGA对,称IDWGA算子为交互密度几何加权集结算子,其表达式为：

将IDWA算子和IDWGA算子统称为交互密度信息集结算子,记为IDA算子。IDA算子具有以下两个特点：一是交互信息数据对A中其诱导分量v体现的是“交互特征”,可以根据需要体现稳定性交互特征,亦可以体现一致性交互特征,因此使用时具有灵活性；二是对交互信息集结时考虑了信息的密度,因此更加全面。故而,交互密度算子可以理解为是专门针对交互评价信息集结而开发的一类特殊集结算子。

2.2 交互数据对的聚类

考虑信息的密度是IDA算子在信息集结时的主要特点之一,因此在对交互信息进行集结之前需要对交互信息（交互数据对）进行聚类。

由于交互数据对具有诱导变量与数据变量这两个分量,因此在对交互数据对进行聚类时,需要同时考虑,需要按照其综合间隔疏密程度对交互数据对进行分组。下面给出交互数据对的分组过程：

步骤1 设n个交互信息数据对组成的交互数据对组为A=｛〈v1,x1〉,〈v2,x2〉,…,〈vn,xn〉｝,首先按照“交互特征”诱导分量vi（i=1,2,…,n）由大到小的顺序对交互数据对进行降序排序,设序化后的交互数据对组为A′=｛〈,x1〉,,x2〉,…,〈,xn〉｝,但不失一般性,仍记序化后的交互数据对组为A。

步骤2 对序化后的交互数据对组A,令Δi= vi-vi+1,i=1,2,…,n-1,这里Δi表示“交互特征”诱导分量vi（i=1,2,…,n）的增量值。

步骤4 令Δ*=max｛Δi|i=1,2,…,n-1｝,定义一空集Br,若0≤（Δ*-Δi）/Δ*≤1/4,则Br=Br+｛Δi｝（i=1,2,…,n-1）。重复上述过程,直到选不出满足条件的Δi。

步骤6 对于分类数r（2≤r≤n-1）,将“交互特征”诱导分量vi（i=1,2,…,n）的增量值Δi,按由大到小的顺序依次选取前r-1个最大的有序增量值Δi,并在产生r-1个Δi的数据之间进行分割,则r个交互数据对的子群A1,…,Ar即为交互数据对组A的r组聚类。

2.3 算子的性质分析

性质1 置换不变性：设A′=｛〈,x1〉,〈, x2〉,…,〈,xn〉｝是交互数据对组A=｛〈v1,x1〉,〈v2,x2〉,…,〈vn,xn〉｝的任一置换,则利用交互密度信息集结算子IDA进行集结后其集结果是一致的,即：

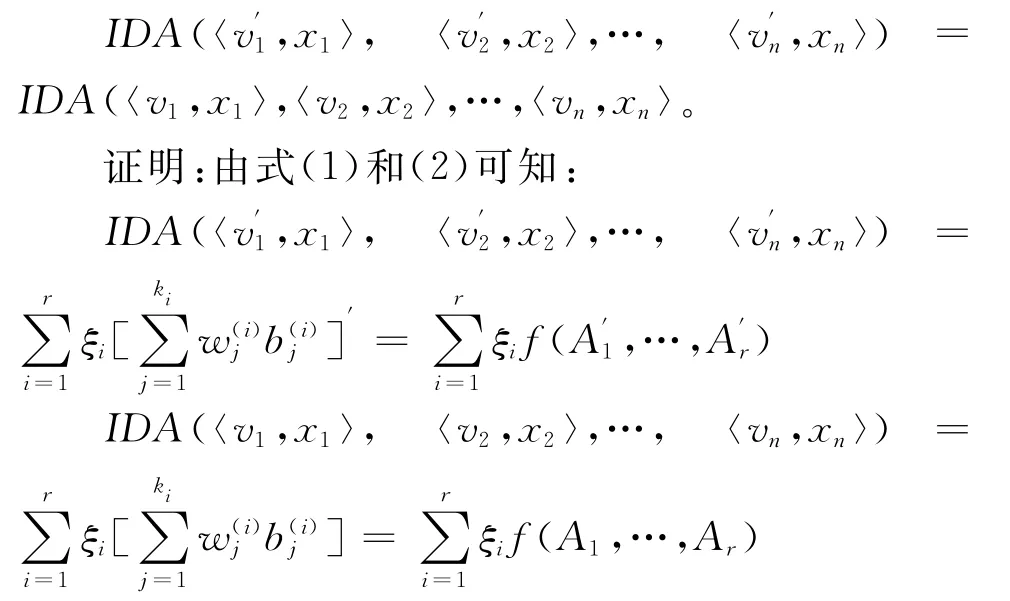
的结论成立。

性质2 幂等性：对任一交互数据对组A=｛〈v1,x1〉,〈v2,x2〉,…,〈vn,xn〉｝,若∀i（i=1,2,…,n）,有vi=v,xi=x,则IDA（〈v1,x1〉,〈v2, x2〉,…,〈vn,xn〉=v。

证明 由于vi=v,xi=x,故交互数据对组A=｛〈v1,x1〉,〈v2,x2〉,…,〈vn,xn〉｝可写成A=｛〈v,x〉,〈v,x〉,…,〈v,x〉｝,设其降序排序后的r组聚类A1,…,Ar,Ai（i=1,2,…,r）中元素为ki个,则：

3 基于交互密度算子的群体评价方法

在利用IDA算子进行群体交互信息集结时,通常需要考虑到三个主要问题：一是由于交互式评价在静态和动态过程中的表现形式不一样,因此在信息集结时,其中“交互特征”诱导分量v的选定较为关键；二是密度权向量ξi（i∈R）的确定；三是IDWA算子和IDWGA算子的选用问题。

3.1 “交互特征”诱导分量的确定

在采用IDWA算子（或IDWGA算子）进行交互信息集结时,集结可分两个方面进行,一是单阶段信息的静态集结,也即“横向”集结；二是多阶段的动态集结,也即“纵向”集结。在“横向”与“纵向”集结时,其“交互特征”诱导分量是有区别的,在单阶段（静态）评价过程中,由于意见的一致性是群体交互过程中更关注的问题,因此在信息集结时可将“交互特征”诱导分量设置为能够体现群体意见“一致性”的指标；而在多阶段（动态）评价过程中,此时专家意见的稳定性是群体交互过程中更关注的问题,因此在信息集结时可将“交互特征”诱导分量设置为能够体现群体意见“稳定性”的指标。群体意见“横向”上的一致性,可以通过同一交互阶段tk中个体si之间评价意见xi（tk）（i=1,2,…,m）的接近程度来衡量；群体意见“纵向”上的一致性,可以通过不同交互阶段中群体评价意见xii（tk）（k=1,2,…,l）的波动程度来衡量。因此这里分别给出群体意见间的一致性和整体稳定性两个“交互特征”诱导指标。

定义3 称τi（tk）（i=1,2,…,m）为第tk轮交互中专家si与专家群的意见一致性“交互特征”诱导指标,计算式为

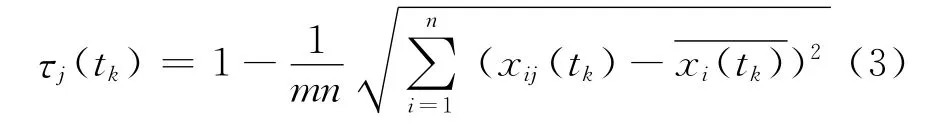
定义4 称η（tk）为第tk（k=1,2,…,l）轮意见xii（tk）相对第tk-1轮意见xii（tk-1）的整体稳定性“交互特征”诱导指标,计算式为

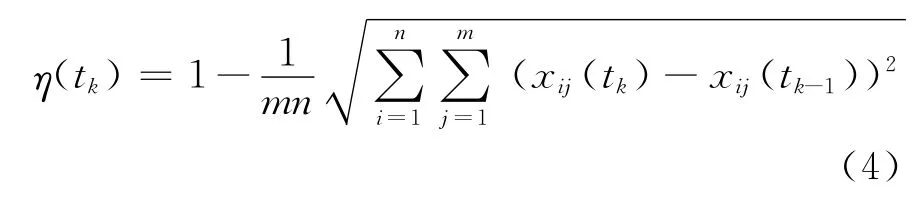
由式（4）可以看出,群体意见的整体稳定性由群体评价信息在“纵向”上的偏差程度所决定。不失一般性,记整体稳定性向量为η=（η（t1）,η（t2）,…,η（tl）T。

3.2 权重向量的确定

对序化后的群体数据组P1,P2…,Pr,这里分别给出群体密度加权向量的熵I和“疏密信息偏好度”λ[10］的定义式：

熵是热力学中的一个名词,在信息论中又称为平均信息量,它是信息的一个度量。熵值越大,则它所含有的信息量越小。群体密度加权向量的熵反映了对样本的集结过程中权重包含信息的程度。

特别地,当ξ=（1,0,…,0）T时,λ=1；当ξ=（0,0,…,1）T时,λ=0；当ξ=（1/r,1/r,…, 1/r）T,λ=0.5。

“疏密信息偏好度”λ的大小体现了算子集结过程中信息疏密的重视程度（见表1）,即当λ越接近0时,表明评价者越注重信息密度最大的数据；当λ越接近1时,表明评价者越注重信息密度最小的数据；当λ=0.5时,表明评价者对信息疏密的重视程度相同,没有特殊偏好。

表1 “疏密信息偏好度”的标度参考表

确定ξi的准则：在事先给定“疏密信息偏好度”λ的情况下,以尽可能地挖掘群体评价的信息和兼顾信息分布密度在重视程度上的差异为标准来寻找适合信息集结的群体密度权向量。用数学语言描述该准则,即求解非线性规划问题：

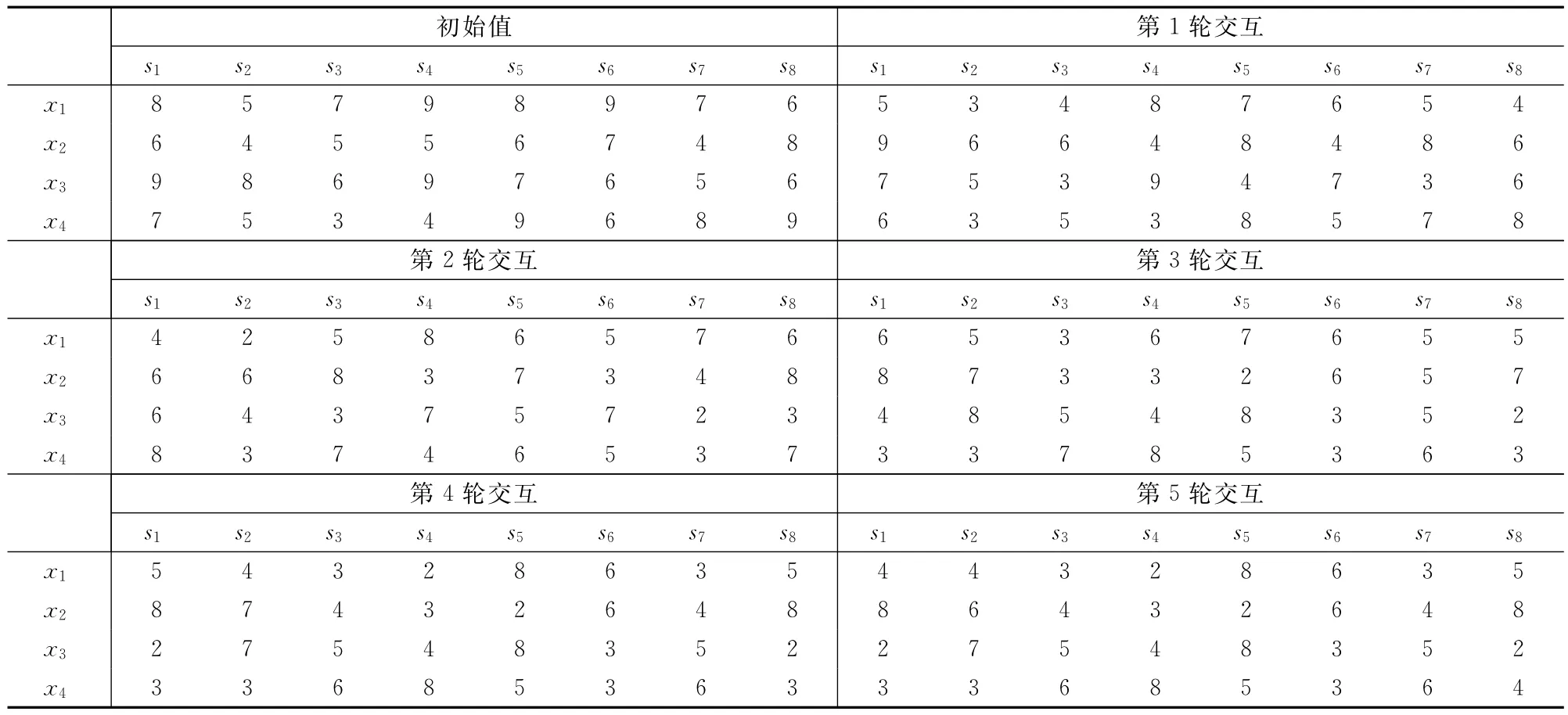
表2 多轮群体交互评价数据表

3.3 算子的选用

从式（1）和式（2）中可以明显的看出IDWA与IDWGA算子分别是“和性”的和“积性”的,由于这种特性使两种算子在数据集结的过程中的侧重点不同。IDWA算子突出了系统发展过程的功能性,即允许评价对象各时期的评价值有较强的互补性,具有“一俊遮百丑”的特点；TDWGA算子突出了系统发展过程的均衡性（或协调性）,即强调评价对象各时期发展的均衡性,是木桶原理的集中体现,防止系统发展过程出现“短板子”的现象。IDWA与IDWGA算子在数据集结上各有利弊可以视具体情况进行选择,如将两种算子组合成同时兼顾功能性与均衡性的混合模型将更为合理。

4 应用举例

考虑一个8（m=8）人评价小组对4（n=4）个备选投资项目进行评选的情形,8个评价者对4个备选投资项目的意见不一致（有的看中高收入,有的看中低风险）,假设经过4（l=4）轮群体评价（其交互终止条件设定为：当某连续2轮交互过程中,其整体稳定性指标η（tk）≥0.9,则交互终止）,相应的群体交互评价数据表见表2,下面利用本文提出的交互密度算子对群体交互评价信息进行集结,限于篇幅,详细计算过程略。

基于交互密度算子的交互式群体评价信息集结过程如下：

（1）计算各轮次的一致性“交互特征”诱导指标值向量τ（tk）（k=1,2,3,4）。运用式（3）计算得一致性“交互特征”诱导指标值向量分别为：τ（t1）=（0.891,0.875,0.897,0.797,0.868,0.894,0.882, 0.902）T,τ（t2）=（0.883,0.850,0.881,0.835, 0.940,0.872,0.849,0.880）T,τ（t3）=（0.874, 0.855,0.861,0.856,0.832,0.901,0.953,0.862）T, τ（t4）=（0.854,0.875,0.913,0.829,0.788,0.901, 0.913,0.854）T,τ（t5）=（0.850,0.886,0.920,0.836, 0.788,0.895,0.920,0.860）T。

（2）“横向”信息交互数据对的聚类。以方案x1的交互信息聚类为例进行说明,其在第一轮的交互数据对组为A=｛〈0.891,5〉,〈0.875,3〉,〈0.897, 4〉,〈0.797,8〉,〈0.868,7〉,〈0.894,6〉,〈0.882,5〉,〈0.902,4〉｝,序化后的交互数据对组为A=｛〈0.902,4〉,〈0.897,4〉,〈0.894,6〉,〈0.891,5〉,〈0.882,5〉,〈0.875,3〉,〈0.868,7〉,〈0.797,8〉｝,按照交互数据对的分组方法,其分组结果为：A1=｛〈0.902,4〉,〈0.897,4〉,〈0.894,6〉,〈0.891,5〉｝, A2=｛〈0.882,5〉｝,A3=｛〈0.875,3〉,〈0.868, 7〉｝,A4=｛〈0.797,8〉｝。同理,其在第二轮的分组结果为：A1=｛〈0.940,6〉｝,A2=｛〈0.883,4〉,〈0.881,5〉,〈0.880,6〉｝,A3=｛〈0.872,5〉｝A4=｛〈0.850,2〉,〈0.849,7〉｝,A5=｛〈0.35,8〉｝；在第三轮的分组结果为：A1=｛〈0.935,5〉｝,A2=｛〈0.901,6〉｝A3=｛〈0.874,6〉｝,A4=｛〈0.862, 5〉,〈0.861,3〉,〈0.856,6〉,〈0.855,5〉｝,A5=｛〈0.832,7〉｝；在第四轮的分组结果为：A1=｛〈0.913,3〉,〈0.913,3〉,〈0.901,6〉｝,A2=｛〈0.875,4〉,〈0.854,5〉,〈0.854,5〉｝,A3=｛〈0.829,2〉｝,A4=｛〈0.788,8〉｝；在第五轮的分组结果为：A1=｛〈0.920,3〉,〈0.920,3〉｝,A2=｛〈0.895,4〉,〈0.886,4〉｝,A3=｛〈0.860,5〉,〈0.850,4〉｝,A4=｛〈0.836,2〉,〈0.788,8〉｝。

（3）评价信息的“横向”集结。为简化计算,假设评价专家的重要性相当,其重要性权重向量为w=（1/8,1/8,1/8,1/8,1/8,1/8,1/8,1/8）T,因此采用交互密度信息集结算子（IDWA）计算得“横向”信息集结结果为：y（t1）=（5.250,6.375,5.500, 5.625）T,y（t2）=（5.375,5.625,4.625,5.375）T, y（t3）=（5.375,5.125,4.875,4.750）T,y（t4）=（4.500,5.250,4.500,4.625）T,y（t5）=（4.375, 5.125,4.500,4.750）T。

（4）计算整体稳定性的“交互特征”诱导指标值向量η。运用式（4）计算得整体稳定性的“交互特征”诱导指标值向量为：η=（0.632,0.694,0.523, 0.823,0.946）T。

（5）“纵向”信息交互数据对的聚类。同样,以方案x1在各轮交互中的信息聚类为例进行说明,其交互数据对组为A=｛〈0.632,5.250〉,〈0.694, 5.375〉,〈0.523,5.375〉,〈0.823,4.500〉,〈0.946, 4.375〉｝,序化后的交互数据对组为A=｛〈0.946, 4.375〉,〈0.823,4.500〉,〈0.694,5.375〉,〈0.632, 5.250〉,〈0.523,5.375〉｝,按照交互数据对的分组方法,其分组结果为：A1=｛〈0.946,4.375〉｝,A2=｛〈0.823,4.500〉｝,A3=｛〈0.694,5.375〉,〈0.632,5.250〉｝,A4=｛〈0.523,5.375〉｝。

（6）评价信息的“纵向”集结。取λ=0.1（非常重视信息密度高的群体意见）,将相关参数代入,求解规划模型（7）,计算得信息密度权向量为ξ=（0.125,0.125,0.025,0.601）T,然后采用交互密度信息集结算子（IDWA）,计算得“纵向”信息集结结果,也即最终的综合评价结果为：y=（4.975, 5.500,4.800,5.025）T,因此评价方案排序为x2≻x4≻x1≻x3。其中值得注意的是,方案x2与x4其数据整体差别不大,但是方案x2的数据分布相对较集中,一致性“交互特征”诱导指标相对较好,因此方案x2的最终综合评价结果要优于方案x4,这也是利用IDA算子进行交互信息集结的一个主要特点。

5 结语

针对交互式群体评价信息集结的复杂性,并考虑到交互信息的分布问题,本文提出了具有一种应用性较强的信息集结算子——交互密度信息集结（IDA）算子,并对算子的相关性质进行了分析。IDA算子具有以下几个特点：

（1）针对性较强。以往的信息集结算子主要是针对一般的数据信息,因此普适性强,而针对性较弱。交互式群体评价信息集结问题自身具有特殊性,本文提出的交互密度信息集结（IDWA）算子是专门针对该类问题而开发的一种新的算子,因此针对性和应用性较强。

（2）聚类方式体现了集结目标。IDA算子是依据评价信息的一致性数据特征的分布疏密程度来对诱导数据对进行聚类的,这符合交互式群体评价信息集结的目标导向。

（3）考虑了信息分布密度。利用IDA算子进行信息集结时,不但考虑了交互信息数据自身的固有特征,而且还考虑了他的分布特征,即从信息密度的角度进行了拓展。

（4）集结具有立体性。利用IDA算子对多阶段交互式评价信息进行集结时,从单阶段横向信息与多阶段纵向信息均进行了集结,体现了交互评价信息时间上的立体性特征。

（5）适用于规模较大的情形。由于本文方法是在大规模群体评价信息密度的基础上进行动态集结的,因此,群体规模越大,则集结效果越明显,但与此同时,其信息处理量则对应增加,可以利用相应计算机软件进行处理。

另外,本文仅从点值角度对交互密度信息集结算子（IDWA）进行了应用,事实上完全可以区间数、语言信息、模糊数据等角度进行探讨；同时,本文仅从诱导加权平均（算术与几何）的角度探讨了IDA算子,事实上还可以从诱导有序加权平均的角度进行拓展,即探讨交互密度有序加权算子（IDOA算子）,本文的下一步研究工作将主要从该方面展开。

[1］Wu Zhibin,Xu Jiuping.A concise consensus support model for group decision making with reciprocal preference relations based on deviation measures[J］.Fuzzy sets and systems,2012,206：58-73.

[2］Kugler T,Kausel E E,Kocher M G.Are groups more rational than individuals？A review of interactive decision making in groups[J］.Wiley interdisciplinary reviews-cognitive science,2012,3（4）：471-482.

[3］Su Zhixin,Chen Mingyuan,Xia Guoping.An interactive method for dynamic intuitionistic fuzzy multi-attribute group decision making[J］.Expert systems with applica-tion,2011,38（12）：15286-15295.

[4］Xiong Jian,Chen Yingwu,Yang Kewei.A decision support model for multi-attribute group decision making using a multi-objective optimization approach[J］.International journal of computational intelligence,2013,6（2）：337-353.

[5］Xu Zeshui,Chen Jian.An interactive method for fuzzy multiple attribute group decision making[J］.Information Sciences,2007,177（1）：248-263.

[6］Fedrizzi M,Giove S.Incomplete pairwise comparison and consistency optimization[J］.European Iournal of Operational Research,2007,183（1）：303-313.

[7］Kim S H,Ahn B S.Interactive group decision making procedure under incomplete information[J］.European Journal of Operational Research,1999,116（3）：498-507.

[8］邸强,朱建军,刘思峰,等.基于两类残缺偏好信息的交互式群决策方法研究[J］.中国管理科学,2008,16（S1）：277-181.

[9］徐泽水.一种部分概率信息下的策略优选方法及其应用[[J］.系统工程学报,2001,16（3）：228-231.

[10］Chuu S J.Interactive group decision-making using a fuzzy linguistic approach for evaluating the flexibility in a supply chain[J］.European Journal of Operational Research,2011,,213（1）：279-289.

[11］Xu Zeshui.Interactive group decision making procedure based on uncertain multiplicative linguistic preference relations[J］.Journal of systems engineering and electronics,2010,21（3）：408-415.

[12］Sun Xiaoyan,Yang Lei,Gong Dunwei.Interactive genetic algorithm assisted with collective intelligence from group decision making[C］.Proceedings of IEEE International Conference on Fuzzy Systems,Brisbane, Australia,June 10-15,2012.

[13］Koksalan M,Ozpeynirci S B.An interactive sorting method for additive utility functions[J］.Computers& Operations Research,2009,36（9）：2565-2572.

[14］陈建中,徐玖平.群决策的交互式TOPSIS方法及其应用[[J］.系统工程学报,2008,23（3）：276-281.

[15］席酉民,井辉,肖宏文,等.和谐主题与和谐机制一致性关系的实证研究[J］.管理科学学报,2008,11（5）：94-101.

[16］杜元伟.基于和谐思想的交互式多属性群决策方法[J］.系统工程学报,2011,26（1）：24-26.

[17］张发明,郭亚军,易平涛.一种主客方协作式群体评价方法及其应用[J］.中国管理科学,2010,18（4）：145-151.

[18］张发明,郭亚军,易平涛.基于二维密度加权算子的群体评价信息集结方法[J］.系统管理学报,2009,18（4）：397-401.

A Method of Interactive Group Evaluation Information Aggregation Based on Interactive Density Operator and Its Application

ZHANG Fa-ming
（School of Economics&Management,Nanchang University,Nanchang 330031,China）

A difficulty for interactive group evaluation is the aggregation of evaluation information.The relevant researches in China rarely discuss the issue from the perspective of information aggregation operator. To make up this deficiency,and taking into consideration that information distribution density is an important character of interactive group evaluation information aggregation,a new method of interactive group evaluation information aggregation method is proposed in this paper based on interactive density operator. Two new operators-interactive density arithmetical weighted operator（IDWA）and interactive density geometrical weighted operator（IDWGA）are proposed,and relevant properties of the two new operators are discussed.In addition,the way to determine the density weighted factors of the two operators is introduced.At last,the new method is applied in an example to illustrate its effectiveness.A new research idea of interactive group evaluation information aggregation problems is provided in this paper.

group evaluation；IDWA operator；IDWGA operator；information aggregation

C934

A

1003-207（2014）12-0142-07

2012-11-22；

2013-04-030

国家自然科学基金资助项目（71361021,71001048, 71261007）；国家社会科学基金资助项目（11BGL063, 12AZD042）；江西省教育厅科技资助项目（GJJ14113）；江西省社会科学“十二五规划”项目（13GL38）；江西省学位与研究生教改研究重点项目（JXYJG-2014-002）

张发明（1980-）,男（汉族）,江西临川人,南昌大学赣江特聘教授,博士生导师,研究方向：综合评价与决策支持.