基于复杂网络理论的股票指标关联性实证分析

张来军,杨治辉,路飞飞

（1.南京大学商学院,江苏南京 210093；

2.安徽财经大学统计与应用数学学院,安徽蚌埠 233000）

基于复杂网络理论的股票指标关联性实证分析

张来军1,杨治辉2,路飞飞2

（1.南京大学商学院,江苏南京 210093；

2.安徽财经大学统计与应用数学学院,安徽蚌埠 233000）

复杂网络理论是研究股票市场内在结构和功能的有力工具,股票指标的关联性已成为研究股票市场的一个新视角。基于复杂网络理论对深沪300指数（2011年7月28至2012年2月28）构建网络拓扑结构。利用DFA进行数据筛选,计算筛选后数据的股票指标的绝对相关系数。根据股票指标的绝对相关系数概率分布确定阈值,构建网络拓扑结构,计算股票指标的网络统计特征指标,分析收益率、成交量、市盈率的网络结构。研究结果表明,股票收益率和成交量指标的具有较强的关联性,具有小世界性质；市盈率指标具有较弱的关联性,不具有小世界性质,是随机网络且受外界影响较大、效率低下,风险比较大。

复杂网络；DFA；股票指标；拓扑结构

1 引言

复杂网络理论可以用来描述大多数含有相互作用的实际系统,比如股票指标间的关联性。大量包含多个体和多个体相互作用的系统都可以抽象为复杂网络,其中每一个个体对应网络的一个顶点,个体之间的联系或相互作用对应连接顶点的边。这种描述方法已被广泛应用于各种实际系统的研究,如WWW网络、Internet网络、神经元网络等,这些实际网络具有与传统规则或随机网络[1］不同的拓扑性质。近年来,人们运用复杂网络理论来研究金融市场[2］（特别是股票市场）,主要有研究股票关联网络的基本拓扑统计性质[3］和运用股票关联网络挖掘内在的等级聚类结构。对于后者,传统的金融研究文献提出了许多方法,如主成分分析法等,然而这些方法并不能准确的表述这一复杂系统间的关系。股票之间的关联和聚类结构对于投资理论和风险管理具有重要的意义,基于复杂网络的分析提供了一种独特的视角和方法。由于各股票市场具有不同的运行环境和发展历程[4］,已有的外国股票市场关联网络[5］的分析结论不一定适用于中国,而目前中国的相关研究尚不多见。因此本文对现有的复杂网络实证分析方法[6］进行完善,以具有代表性的沪深300指数成分股票为研究目标,运用消除趋势波动分析法（Deterministic Finite Automaton,DFA）算法构建相应的股票指标关联网络[7］,分析网络的拓扑性质；根据绝对相关系数确定阈值计算不同阈值下的网络特征指标,构建网络结构拓扑,分析收益率、成交量、市盈率的关联性。

股票市场是一种特殊的投资市场,对股票市场的深入研究有助于人们了解股市的结构,分析股市风险和判断股市未来变化趋势。然而当前针对股价的波动性进行了大量的研究工作。Fama和French[25］认为,市盈率与股票收益率之间存在负相关；而Fuller,Huberts和Levinson[26］则发现,与低市盈率的股票相比,高市盈率股票具有较高的收益率。何诚颖[8］研究了中国股市市盈率分布特征,实证分析了1995年底至2002年底市场个股市盈率结构状况,得出低于市场平均市盈率的行业股票未来总是比明显高于市场平均市盈率的行业股票有更好的表现的结论。实际上其结论与2009年以来中国股市的个股表现不相符的。颜竹梅,刘亦文,黄静寅[9］研究了中国股市市盈率变化趋势得出沪深股市市盈率波动的上限处于比较高的水平,与其他国际市场未表现出一致性。赵静梅,吴风云[10］认为数字崇拜影响投资者的选股行为和股票的价格,对上海证券交易所股票代码尾数为8的股票（8股票）进行了研究,发现8股票长期异常收益率偏低,长期跌幅较大。事实上反例很多。陈浪南,孙坚强[11］分析股票市场资产收益的跳跃行为,采用中国的上证综合指数、香港恒生指数、台湾加权指数和美国的道琼斯工业指数、纳斯达克综合指数的数据对资产收益的跳行为进行实证检验。

在复杂网络理论研究不断深入的同时,对复杂网络理论的应用性研究已开始从计算机控制学科快速扩散到社会经济管理领域。而金融市场的复杂性研究成为经济管理复杂性研究的重要领域,利用复杂网络理论来研究金融市场尤其是股票证券市场的复杂性受到了众多学者的重视。近年来,许多专家学者利用复杂网络理论对证券市场进行了研究。Kim[12］等人就标准普尔500只股票的股票价格关联性,以公司和公司股票为节点构建了一个无标度加权网络,发现节点的边权和的绝对值大小呈现无标度特性；Onnela[13］等研究了纽约证券交易所477只股票形成的关联网络拓扑性质,如派系数量和规模、平均聚集系数等,并将实际网络与同等规模的随机网络进行了对比；Lee[14］等研究了韩国KOSPI 200只股票关联网络的平均路径长度、度分布等基本拓扑统计性质；黄玮强[15］等人根据复杂网络理论利用阈值法对中国沪市和深市的1080支股票建立了关联网络模型,分析了该网络的拓扑结构特征,发现该网络具有对随机攻击的鲁棒性和对蓄意攻击显示出脆弱性；还有许多国内外专家利用复杂网络理论来研究证券市场[16-18］。

根据股票价格波动（收益率）相关性信息构建的初始关联网络为全连接网络,事实上在全连接关联网络的所有边中,大部分边所反映的股票关联信息是噪声,仅有部分边包含真正有用的关联信息,因此需要从初始关联网络中过滤掉多余的边构建真正意义上的关联网络。Kim、Onnela和Lee[12-14］构建的股票关联网络均是初始关联网络的最小生成树,由于最小生成树的拓扑结构较为简单,因此会出现过度过滤现象从而丢失掉一些有用的边信息。为弥补最小生成树的缺陷,Tumminello[19］等提出了平面最大过滤图算法,运用该算法生成的网络能反映更复杂的拓扑结构；Tumminello[20］等运用最大过滤图算法构建了纽约股票交易所的300只股票关联网络,研究了网络拓扑性质（如平均最短路径、节点介数和度数）随股价记录时间周期变动而变化的规律。

然而当前针对股价波动的研究工作,大都只针对于个股指标之间关系而展开,缺乏对系统的分析和认识,并不能从整体上把握股票市场的运作模式,这无疑是理论研究工作中的一块亟待开发的领域。而伴随着复杂网络和混沌系统相关知识体系的建立,人们越来越多地将各种经济、社会活动抽象为网络进行分析,以期透过纷繁复杂的表面现象认识其内在的运作规律,同时虽然复杂网络拓扑结构特征的描述与度量、复杂网络建模、复杂网络上的动力学机制以及复杂网络的鲁棒性和脆弱性等方面理论已经有了较为完整的理论雏形,但是复杂网络系统理论在各个领域及学科的实际应用仍然没有完善,还有很多的发展空间,尤其是在经济领域的应用,由于我国经济形势的复杂多变使得复杂系统理论的应用变得更为困难。国内的大多数文献也仅限于研究复杂网络在经济领域中表现出来的一些网络结构特点,并没有从不同角度深层次的分析这些结果特点所蕴含的机理和经济意义,这为进一步研究提供了理论和现实空间。

已有相关研究主要有对股价的波动性的研究、利用复杂网络理论来研究股票市场及简单地从基础理论角度分析网络结构、运用最小生成树或平面最大过滤图算法对关联网络进行处理等。这些研究缺乏系统的分析和认识,并不能从整体上把握股票市场地运行模式。而运用复杂网络研究股票市场也仅限于一些网络结构特征,并没有深层次地分析这些结果蕴含的机理和经济意义。已有研究从股价方面构建网络。本研究运用复杂网络理论,从整体上把握股票市场网络结构,并对其网络结构特征进行系统的分析。

本研究创新地从股票基本指标（收益率、成交量和市盈率）来构建网络,来研究股票指标之间的关联性,而已有研究主要从股价来构建网络。利用消除趋势波动分析法（DFA）对沪深300指数数据进行处理,筛选出实证分析所需要的样本数据,进行有效的预处理,然后通过独立性检验,剔除一些具有短记忆特征的数据,这样一来便避免了最小生成树的不足。依据阈值法建立相关性网络拓扑结构,去除弱相关性指标的干扰。运用UCINET和Pajek软件画出股票指标的网络拓扑图,较为清晰地展示了各支股票的指标之间的关联性,而关联性数值大小也可展示出来,由于显得杂乱故将关联性大小的数值隐藏起来。

2 股票关联网络构建方法[22]

在股票关联网络中节点代表股票,节点之间的连边代表股票价格波动（或其他反映股票关联的度量）之间的相关性,连边的权重表示具体的相关性大小,因此所构建的股票关联网络为无向加权网络,在实际操作中网络用邻接矩阵表示。具体的股票关联网络构建包含3个步骤,（1）计算股票价格波动相关系数矩阵；（2）将相关系数矩阵转化为距离矩阵；（3）在距离矩阵基础上运用阈值法构建最终的股票关联网络。

假设关联网络中包含N只股票,各股票价格的观测时间区间为[t0,t0+T］。在观测区间的任意时点τ（根据需要可以为日或高频数据）股票i的收益率为：

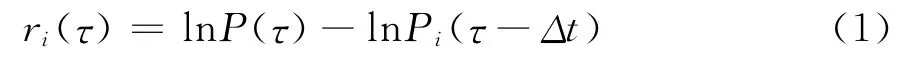
其中,Pi（τ）为时点τ的股票价格,Δt为计算收益率的时间周期。这样每只股票形成具有L个观测值的收益率序列,L的大小取决于T和Δt。根据收益率序列计算任意两只股票i和i在观测区间内股票价格波动的相关系数ρii（Δt）,即：

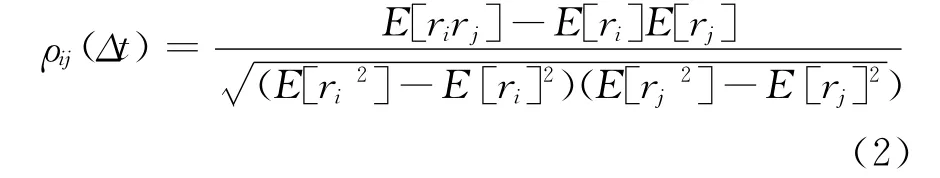
其中,ri为股票i的收益率序列,ri为股票i的收益率序列,E[·］为数学期望,ρii（Δt）∈[-1,1］。根据任意股票之间价格波动相关系数构建相应的N ×N阶相关系数矩阵C,C为对称矩阵,表示为：

其中,cii为相关系数矩阵的第i行第i列元素。一般来说要求相关系数矩阵正定,即L＞N。

任意的股票i和i日平均对数收益率之间的相关系数为Cii,Cii∈[-1,1］当相关系数大于或等于指定的阈值θ时就认为股票i和i之间有边连接,相关系数的大小就是边的权重；相关系数小于指定阈值就认为股票收益率之间没有边,并假设连接节点的边没有方向。

由于股票之间的相关系数集合不满足度量空间的条件,为便于进一步分析关联网络的内在性质,将相关系数ρii（Δt）转化为对应的度量距离d（i,i）,即

式中,股票i与股票i之间的相关系数越大,相应的距离越小。另外度量距离d（i,i）满足度量空间的3个条件,即d（i,i）=0当且仅当

其中,m为不同于i和i的任意其他股票。通过（4）式,相关系数矩阵C转化为距离矩阵D,且Dii=d（i,i）∈[0,2］。

（1）平均路径长度

网络中连接任意两个节点i和i的最短路径上的边数定义为这两个节点之间的距离dii。两个节点之间距离的平均值定义为网络的平均路径长度,记为L,即：

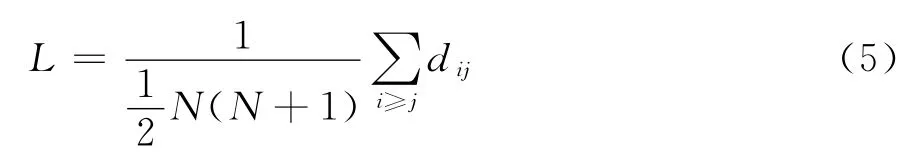
其中N为网络节点数。公式（5）中包含了节点到自身的距离（该距离为零）。

（2）聚类系数

假设网络中的一个节点i有ki条边将它和其他节点连接,那么就有ki个节点围绕在节点i周围,这ki个节点就称为节点i的邻居。显然这个节点ki之间最多有ki（ki+1）/2条边。而这ki个邻居节点包括节点i之间实际存在的边数Ei和总的可能的边数ki（ki+1）/2之比就定义为节点i的聚类系数Ci,即

（3）度与度分布

节点i的度ki定义为与该节点连接的其他节点的数目。从直观上看,一个节点的度越大就意味着这个节点在某种意义上越“重要”。有向网络的度分为出度和入度,网络中所有节点i的度ki的平均值称为网络节点的平均度,记为〈k〉。网络中节点的度的分布情况可以用分布函数P（k）来描述。P（k）表示的是一个随机选定的节点的度恰好为k的概率,在均匀网络中P（k）的分布近似Possion分布。

近年来大量的研究表明,许多实际网络的度分布明显不同于Possion分布,特别的许多实际网络可以用具有适当幂指数γ的幂律形式P（k）∝k-γ来更好的描述（通常情况2≤γ≤3）,幂律分布曲线比Possion指数分布曲线下降缓慢的多。幂律形式P（k）∝k-γ也可以∝表示为log P（k）∝-γlog k,幂律分布也称为无标度（Scale-Free）分布,具有幂律度分布的网络也称无标度网络。

指数拟合优度R是指数方程的整体拟和度,是表达因变量与所有自变量之间的总体关系。R的取值范围是[0,1］,R值越接近1,说明拟和程度越好；反之,R值越接近0,说明拟和程度越差。

（4）阈值

阈值α是使系统行为发生突变的系统状态控制参量数值,又叫临界值。系统的控制参量超过一个阈值后,往往还存在着下一个阈值,进一步改变控制参量,当它超过新的阈值后,就会发生新的突变,使系统进入更高级的有序状态。本文采用阈值法,通过相关系数矩阵的概率分布定义网络阈值α0,当|α -α0|越小,网络越稳定；反之,当|α-α0|越大,网络越不稳定。

3 实证分析

本文选取深沪300指数（2011年7月28至2012年2月28）进行实证分析,因为沪深300指数样本覆盖了沪深市场六成左右的市值,具有良好的市场代表性。它是沪深证券交易所第一次联合发布的反映A股市场整体走势的指数。它的推出,丰富了市场现有的指数体系,增加了一项用于观察市场走势的指标,有利于投资者全面把握市场运行状况,也进一步为指数投资产品的创新和发展提供了基础条件。

我们选取每天的开盘价作为基础数据来计算收益率,因为停盘而导致的数据空缺我们用停盘前最后一天的开盘价来填补空缺。由于停盘期股票不交易,收益率为0,因此上述处理是合理的。

根据DFA算法流程[21］运用Matlab7.0计算得到结果,部分结果如表1：

表1 不同成分股的标度指数

根据上面的计算结果得出结论,首先所有的度指标数几乎都集中在区间[0.5,1］,表明股票价格趋势的确具有长记忆性,当前的价格波动趋势不会影响长期的股票价格。这符合我国股票市场的弱有效性；其次上述计算结果中小于0.5的度指标数所占总样本数的比例不足3%,提出小于0.5的样本不会对股票市场整体结果产生影响,所以可以按照度指标数下限为0.5进行筛选。本文在经过了数据筛选剔除之后搜集了收益率、成交量、市盈率数据样本分别是282、300、285组。

计算出筛选后收益率、成交量、市盈率数据的绝对相关系数,通过Matlab7.0作出相关系数分布图如下：

图1 收益率绝对相关系数概率密度分布

由图1可以看出,收益率绝对相关系数大多数分布在[0.4,0.7］,其中相关系数分布在0.6周围的最多,故可以指定阈值为0.6,收益率绝对相关系数大于或等于0.6,则节点之间有边连接,小于0.6则没有。

图2 成交量绝对相关系数概率密度分布

由图2可以看出,成交量绝对相关系数大多数分布在[0.1,0.4］,其中相关系数分布在0.4周围的最多,故可以指定阈值为0.4,成交量绝对相关系数大于或等于0.4,则节点之间有边连接,小于0.4则没有。

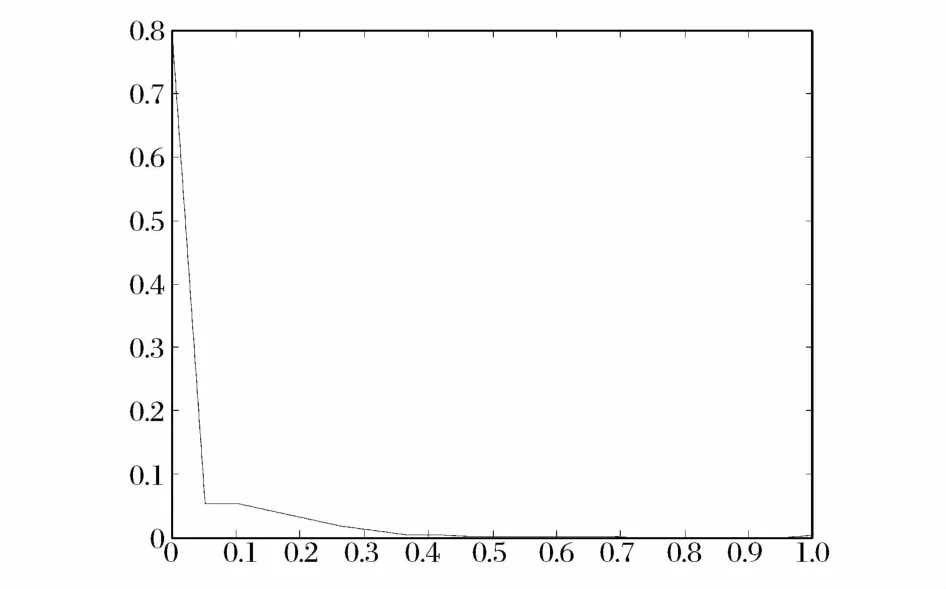
图3 市盈率绝对相关系数概率密度分布

由图3可以看出,市盈率绝对相关系数大多数分布在[0,0.1］,其中相关系数分布在0周围的最多,即大多数股票市盈率之间没有关联性或极小的关联性,故可以指定阈值为0,市盈率绝对相关系数大于或等于0,则节点之间有边连接。

通过UCINET和Pajek软件画出网络结构拓扑图：

图4 股票收益率的网络结构拓扑图

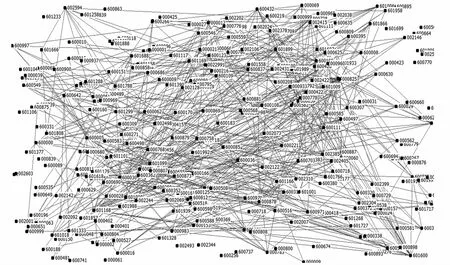
图5 股票成交量的网络结构拓扑图

图6 股票市盈率的网络结构拓扑图

表2 股票各指标网络统计特征

股票网络的统计特征：

计算在绝对相关系数大于指定的阈值的沪深300股票网络的特征指标如平均路径、聚类系数和平均度等,结果见表2。

收益率、成交量这两个股票指标的平均路径长度都非常接近1,这说明各只成分股的指标具有较强的关联性,市盈率的平均路径长度则接近于2,说明成分股市盈率之间具有较弱的关联性。收益率的聚类系数高达95.7%,说明股票日收益率网络具有小世界性质,具有相同属性的股票其收益率波动情况连接紧密；成交量的聚类系数为77.35%,说明股票日收益率网络具有小世界[15］性质,具有相同属性的股票其收益率波动情况连接比较紧密；市盈率的聚类系数为58.53%,说明股票日市盈率不具有小世界的性质,表明了各成分股之间在受到外力作用的情况下相互作用大大减弱,市盈率的多少已经不完全是网络结构自身可以调节的。

统计分析沪深300收益率、成交量、市盈率网络节点度分布得出该网络的度分布均服从幂律分布,因此该网络是无标度网络[16］。表2是分别通过最小二乘法得到的最优阈值下的网络结构的度分布指数。当收益率阈值最大取0.6时,度指数分布小于2,这类网络属于稀疏网络,网络中度值很高的节点（称为HUB点）占所有节点的比例相对较高,这些节点也会对整个复杂网络的拓扑结构具有一定的决定作用；当成交量阈值取0.4时,相应的度分布指数在2～3之间,一方面,为了保证股票的正常交易,必须存在HUB节点；另一方面,由于受到买卖双方对股价认可度存在差异的制约,HUB节点又不能太多,总的线路（边）也不能太多,因而其度分布指数位于2～3之间。当市盈率阈值取0时,相应的度分布指数远大于3,说明该类网络类似于随机网络,这样的网络一方面不能够抵御网络的随机故障（因其类似于随机网络）；另一方面,其效率极低（因为度值很高的HUB节点非常罕见）。可以断言,市盈率网络属于极不稳定且效率极低的一类。表明中国股票市场还不健全,风险较大。

4 结语

本研究主要研究股票市场网络的构建,选取沪深300指数的数据为样本,运用DFA方法筛选实证分析所需要的样本数据,进行有效的预处理,然后通过独立性检验,剔除一些具有短记忆特征的数据,以便实证分析过程可以直接套用数据。在应用了复杂网络理论之后,计算绝对相关系数矩阵,并以其为基础,依据阈值法建立沪深300股票市场收益率、成交量以及市盈率的相关性拓扑网络,运用软件计算出股票市场不同指标的网络统计特征,并经过分析得出不同网络的拓扑结构特性。

研究结果表明,收益率、成交量以及市盈率的度指标数几乎都集中在区间[0.5,1］,表明股票价格趋势的确具有长记忆性,当前的价格波动趋势不会影响长期的股票价格。这符合我国股票市场的弱有效性。收益率绝对相关系数大多数分布在[0.4,0.7］,其中相关系数分布在0.6周围的最多。成交量绝对相关系数大多数分布在[0.1,0.4］,其中相关系数分布在0.4周围的最多。市盈率绝对相关系数大多数分布在[0,0.1］,其中相关系数分布在0周围的最多,即大多数股票市盈率之间没有关联性或极小的关联性。收益率、成交量这两个股票指标的平均路径长度都非常接近1,这说明各只成分股的指标具有较强的关联性,市盈率的平均路径长度则接近于2,说明成分股市盈率之间具有较弱的关联性。收益率的聚类系数高达95.7%,说明股票日收益率网络具有小世界性质,具有相同属性的股票其收益率波动情况连接紧密；成交量的聚类系数为77.35%,说明股票日收益率网络具有小世界[24］性质,具有相同属性的股票其收益率波动情况连接比较紧密；市盈率的聚类系数为58.53%,说明股票日市盈率不具有小世界的性质,表明了各成分股之间在受到外力作用的情况下相互作用大大减弱,市盈率的多少已经不完全是网络结构自身可以调节的。

沪深300收益率、成交量、市盈率网络的度分布均服从幂律分布,因此该网络是无标度网络。收益率度指数分布小于2,这类网络属于稀疏网络,网络中度值很高的节点占所有节点的比例相对较高,这些节点也会对整个复杂网络的拓扑结构具有一定的决定作用；成交量度分布指数在2～3之间,表明一方面,存在HUB节点,为了保证股票的正常交易；另一方面,由于受到买卖双方对股价认可度存在差异的制约,HUB节点又不是太多,总的线路（边）也不是太多。当市盈率阈值取0时,相应的度分布指数远大于3,说明该类网络类似于随机网络,这样的网络一方面不能够抵御网络的随机故障（因其类似于随机网络）；另一方面,其效率极低（因为度值很高的HUB节点非常罕见）。

通过网络统计特征分析了股票市场的情况,得出2011年下半年至2012年2月期间,股票市场不稳定,回报率较低,不利于投资,与实际情况相吻合。本文可为投资者对股票市场的投资提供参考,也可为政府的宏观调控提供借鉴。

以新的角度将复杂网络运用于股票市场,研究股票指标（收益率、成交量和市盈率）的网络结构特征,而不同于已有研究关于股价网络的研究。这种新角度的研究结果与现实情况较为吻合,从而得到实证方面的支持。在数据处理方面,运用DFA方法处理短记忆特征的数据,较好地避免了特殊经济波动对结果的影响。运用UCINET和Pajek软件较清晰地画出网络结构拓扑图,解决了已有相关研究在画上百个节点的拓扑图时较混乱的困扰。运用阈值法建立相关性拓扑网络,去除弱相关性指标的干扰,使得拓扑图更为清晰,也更好地分析网络结构拓扑图的特征指标。本研究使用典型的股票指标作为研究对象,这些股票指标直接反映了股票的运行状况。本文只选取了收益率、成交量和市盈率,而没有考虑其他的股票指标。对于其他指标可能达不到决定股票运行状况,这些指标还需进一步地研究,有待于后续去验证。DFA方法运用已较成熟,对处理复杂网络和混沌系统的数据有较好地效果。

[1］徐红利,周晶,徐薇.基于累积前景理论的随机网络用户均衡模型[J］.管理科学学报,2011,14（07）：1-7.

[2］Caldareli G,Battiston S,Garlaschelli D,et al.Emergence of complexity in financial networks[J］.Lecture Notes in Physics,2005,650（9）：399-423.

[3］Albert R,Barabasi A L.Statistical mechanics of net works [J］.Reviews of Modern Physics,2002,74（1）：47-97.

[4］徐有俊,王小霞,贾金金.中国股市与国际股市联动性分析[J］.经济经纬,2010,（05）：124-128.

[5］Kim H J.Kim I M.Scale-free network in stock markets [J］.Journal of the Korean Physical Society,2002,40（6）：1105-1108.

[6］李亚静,何跃,朱宏泉.中国股市收益率与波动性长记忆性的实证研究[J］.系统工程理论与实践,2003,23（01）：9-14.

[7］汪小帆,李翔,陈关荣.复杂网络理论及其应用[M］.北京：清华大学出版社,2006.

[8］何诚颖.中国股市市盈率分布特征及国际比较研究[J］.经济研究,2003,（9）：74-81,95.

[9］颜竹梅,刘亦文,黄静寅.中国股市市盈率的变化趋势及国际比较[J］,经济与管理,2008,22（5）：25-28.

[10］赵静梅,吴风云.数字崇拜下的金融资产价格异象[J］.经济研究,2009,（6）：129-141.

[11］陈浪南,孙坚强.股票市场资产收益的跳跃行为研究[J］.经济研究,2010,（4）：54-66.

[12］Kim H J,Lee Y,Kahng B,et al.Weighted scale free network in financial correlations[J］.Journal of Physical Society of Japan,2002,71（9）：2133-2136.

[13］Onnela J P,Kaski K,KerteszJ.Clustering and information in correlation based financial networks[J］.The European Physical Journal B,2004,38（2）：353-362.

[14］Lee K E,Lee J W,Hong B H.Complex Networks in a Stock Market[J］.Computer Physics Communications, 2007,177（1-2）：186.

[15］黄玮强,庄新田,姚爽.中国股票关联网络拓扑性质与聚类结构分析[J］.管理科学,2008,21（3）：95-96.

[16］Tibely G,Onnela J P,Saramäki J,et al.Spectrum,intensity and coherence in weighted networks of a financial market.Physical A,2006,370（1）：145-150.

[17］Eom C,DHG,Kim S.Deterministic factors of stock networks based uncross-correlation in financial market. Physical A,2007,（383）：139-146.

[18］Tabak B M,Serra T R,Cajueiro Do.Topological properties of stock market networks：The case of Brazil [J］.Physical A：Statistical Mechanics and its Applications,2010,389（16）：3240-3249.

[19］Tumminello M,Aste T,Matteo T D,et al.A tool for filtering information in complex systems[J］.Proceedings of the National Academy of Sciences of the United States of America,2005,102（30）：10421-10426.

[20］Tumminello M,Matteo T D,Aste T,et al.Correlation based networks of equity returns sampled at different time horizons[J］.The European Physical Journal B,2007,55（2）：209-217.

[21］黄小原,庄新田,张泉.股市波动的标度无关性算法及应用研究[J］.管理科学学报,2001,4（6）：55-59.

[22］蔡世民,洪磊,傅忠谦,等.基于复杂网络的金融市场网络结构实证研究[J］.复杂系统与复杂性科学,2011,8（03）：29-33.

[23］Xian Yubo,Mei Lin.Adaptive expectation,complex network and the dynamic of standard diffusion—research based on computational economics[J］.Journal of Management Sciences,2007,20（4）：62-71.

[24］Barabási A L,Bonabeau E.Scale-free networks[J］. Scientific American,2003,288（5）：60-69.

[25］Fama E F,French K R.Common risk factors in the returns on stocks and bonds[J］.Journal of Financial E-conomics,1993,33（1）：3-56.

[26］Fuller R J,Huberts L C,Levinson M J.Returns to EIP strategies,higgledy-piggledy growth,analysts' forecast errors,and omitled risk factors[J］.The Journal of Portfolio Management,1993,19（2）：13-24.

Empirical Analysis of Relevance of Stock Indicators Based on Complex Network Theory

ZHANG Lai-jun1,YANG Zhi-hui2,LU Fei-fei2
（1.School of Business,Nanjing University,Nanjing 210093,China；2.School of Statistics&Applied Mathematics,Anhui University of Finance&Economics,Bengbu 233000,China）

The complex network theory is a powerful tool to study the internal structure and function of the stock market.The research of the relevance of stock indicators has become a new perspective in the research of stock market.Traditional financial research using equity-linked network to dig intrinsic clustering structure,lack of formulation of the relationship between the complex structures.This paper based on complex network theory to build the network topology on CSI 300 Index（July 28 2011-February 28 2012）, the relationship between the complex structures is analyzed,the existing empirical analysis methods of complex network are improved.The data is tiltered by DFA,and the absolute correlation coefficient of the stock index is calculated.According to the absolute correlation coefficients of stock index probability distribution,the threshold is determined and build the network topology is build.Network statistics characteristic index of the stock is calculated,and the network structure of the rate of return,trading volume and price-earnings ratio are analyzed.The results show that the stock returns and trading volume indicators have strong correlation with the small-world character,while price-earnings ratio index has a weak correlation,and does not have the small-world character,and is a random network that subject to outside influence with low efficiency and high-risk.Such new tools and empirical results are useful to study the relevance and empirical findings of stock indicators in China′s financial market.

complex network；the DFA；stock indicators；topology

F830.9

A

1003-207（2014）12-0085-08

2012-09-10；

2013-04-20

张来军（1991-）,男（汉族）,江苏盐城人,南京大学商学院,硕士研究生,研究方向：产业经济学.