低阶对称双随机矩阵逆特征值问题的通解

杨尚俊

(安徽大学数学科学学院，安徽合肥230039)

低阶对称双随机矩阵逆特征值问题的通解

杨尚俊

(安徽大学数学科学学院，安徽合肥230039)

对给定的实或复n－重Λ={λ1，…，λn}，决定是否存在以Λ为谱的非负(随机)矩阵的问题称为非负(随机)矩阵逆特征值问题，这一直是非负矩阵理论中尚未完全解决的一个研究热点.作者曾对n∈{2，3，4，5}，研究n阶双随机矩阵逆特征值问题有解的充分条件并给出相应解的公式.最近，又对任意正整数n，先给出行和为常数的对称矩阵的逆特征值问题的充要条件和解的公式，后给出对称随机矩阵逆特征值问题有解的两种充分条件和解的公式.论文在提出任意阶对称随机矩阵逆特征值问题通解的概念和3阶对称随机矩阵逆特征值问题完全通解的概念之后，首先给出3阶对称随机矩阵逆特征值问题存在完全通解的充要条件和完全通解的公式;其次给出3阶对称随机矩阵逆特征值问题存在通解的充要条件和通解的公式;最后给出4阶对称随机矩阵逆特征值问题有解的几种充分条件和相应解的公式.

逆特征值问题的通解;对称双随机矩阵逆特征值问题;特殊正交矩阵

对给定的实或复n－重Λ={λ1，…，λn}，决定是否存在以Λ为谱的非负(随机)矩阵的问题称为非负(随机)矩阵逆特征值问题.由于非负矩阵(随机)逆特征值问题具有深远理论兴趣和广泛应用价值，它一直是矩阵论研究的一个热门课题［1－12］，并远未得到满意解决.文［11］对n∈{2，3，4，5}研究n阶双随机矩阵逆特征值问题有解的充分条件并给出相应解的公式.文［12］对任意正整数n先给出行和为常数的对称矩阵的逆特征值问题的充要条件和解的公式，后给出对称随机矩阵逆特征值问题有解的两种充分条件和解的公式.论文提出任意阶对称随机矩阵逆特征值问题通解的概念和3阶对称随机矩阵逆特征值问题完全通解的概念.

1 预备知识

沿用文［12］的定义.如果n阶对称矩阵A的n个特征值依次是λ1，…，λn，则称A以给定的实n－重Λ=(λ1，λ2，…，λn)(n＞1)为谱;有一列是的n阶正交矩阵S称为是一个n阶特殊正交矩阵;同阶方阵A，B称为是置换相似的，如果存在置换矩阵H使得B=HAH*.

定理1［12］对称方阵A以Λ=(λ1，λ2，…，λn)(n＞1，λ1≥λ2≥…≥λn)为谱并且行和全为λk(k∈ {1，…，n})的充分必要条件是存在n阶特殊正交矩阵Sn=(ξ1，ξ2，…，ξn)，un(列分块形式)使得

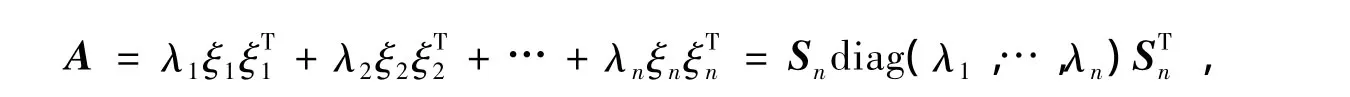
从而ξ1，…，ξn是A的正交标准特征向量组，上式称为由n阶特殊正交矩阵Sn决定的A的谱分解式［12］.

定理2任何3阶对称矩阵都置换相似于下列矩阵簇

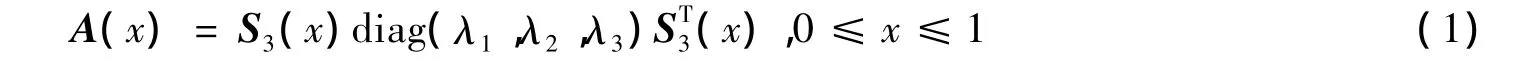
中的某个矩阵，其中

2 3阶对称随机矩阵逆特征值问题的通解和完全通解

命题1存在以Λ=(1=λ1，λ2)为谱的2阶对称随机矩阵的充要条件是1≥λ2≥-1.当上述条件满足时，对称随机矩阵逆特征值问题有唯一解

证明必要性由随机矩阵的谱半径是1直接推出.充分性显然，因以Λ为谱的矩阵(3)在条件1≥ λ2≥-1下是对称随机矩阵.下证解的唯一性.若A是以Λ为谱的对称随机矩阵，则是A的对应特征值1的单位特征向量，对应特征值λ2的单位特征向量是与u2正交的单位向量:，从而.所以，矩阵(3)在条件1≥λ2≥ -1下是唯一的以Λ为谱的对称随机矩阵.

引理1令

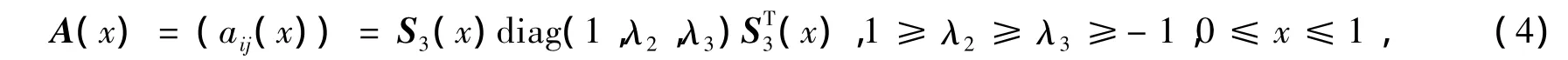
其中:S3(x)=(u3，ξ2(x)，ξ3(x))(列分块形式)是由(2)式定义的特殊正交矩阵簇，则由(4)式定义的以Λ=(1=λ1，λ2，λ3)为谱、并且行和全为1对称矩阵簇(定理1)满足

证明因为

其中:α=2x2+2x+2＞0，x∈［0，1］.公式(5)给出

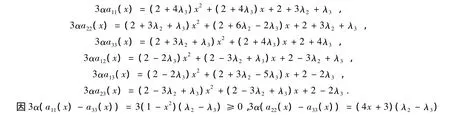
≥0，蕴含min{a11(x)，a22(x)，a33(x)}=a33(x)，0≤x≤1.当2+3λ2+λ3＞0时，有

当2+3λ2+λ3≤0时，有

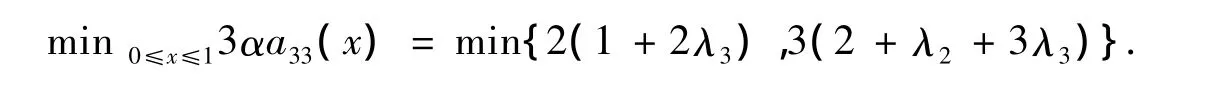
因为1+2λ2≥1+2λ3，2+λ2+3λ3≥2+4λ3=2(1+2λ3)，所以

因为2+3λ2-5λ3≥2-2λ3≥2-3λ2+λ3蕴含a13(x)≥a23(x)，0≤x≤1.再注意到3α(a23(x)－a12(x))=3(1－x2)(λ2－λ3)≥0，有min{a12(x)，a13(x)，a23(x)}=a12(x)，0≤x≤1.当2－2λ3＞0时，有

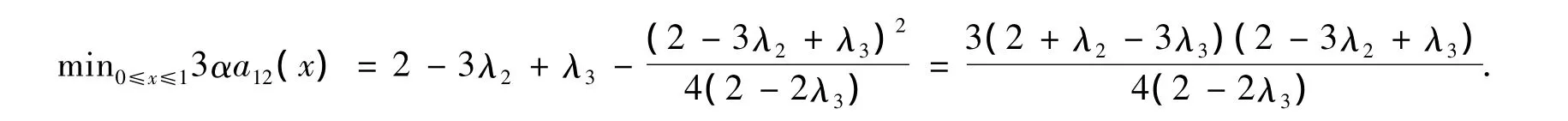
当2-2λ3=0时，有

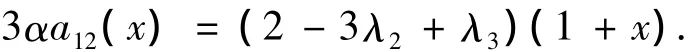
因为2+λ2-3λ3≥0，2-2λ3≥0，所以，

定义1 n阶对称随机矩阵的集合Ω，称为以已知实n重Λ=(1=λ1，λ2，…，λn)(1＞λ2≥…≥λn≥-1)为谱的n阶对称随机矩阵逆特征值问题的通解，如果Ω的每个矩阵都是该逆特征值问题的解，并且该逆特征值问题的任何一个解都与Ω的某个矩阵置换相似.如果(4)(即(5))给出的以Λ=(1=λ1，λ2，λ3)(1≥λ2≥λ3≥-1)为谱的矩阵簇A(x)，0≤x≤1全是随机矩阵，则称它为以Λ为谱的3阶对称随机矩阵逆特征值问题的完全通解.

注1由命题1知:存在以Λ=(1=λ1，λ2)为谱的2阶对称随机矩阵逆特征值问题的通解的充要条件是1≥λ2≥-1，并且该通解是一元集显而易见，3阶对称随机矩阵逆特征值问题的完全通解A(x)的参数x定义在整个闭区间［0，1］上，而3阶对称随机矩阵逆特征值问题的非完全通解A(x)的参数x则只能是定义在［0，1］的某个真子集上.

定理3存在以Λ=(1=λ1，λ2，λ3)(1≥λ2≥λ3≥-1)为谱的3阶对称随机矩阵逆特征值问题的完全通解充要条件是

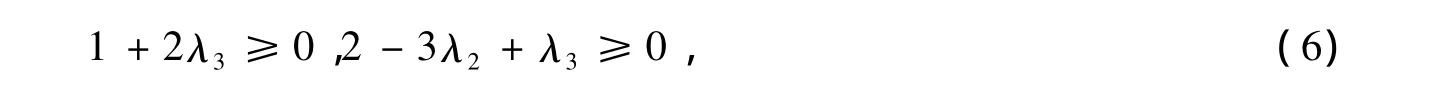
并且该通解由(5)给出.

证明按定理2，任何以Λ为谱的、行和全为1的任何3阶对称矩阵(包括任何对称随机矩阵在内)，必须置换相似于(5)(即(1))中的某个矩阵A(x)=S3(x)diag(1，λ2，λ3)ST3(x)，x∈［0，1］.按引理1，条件(6)是对每个x∈［0，1］，(5)(即(4))的矩阵A(x)都是非负矩阵，即都是对称随机矩阵的充要条件.这就证明，(6)是3阶对称随机矩阵逆特征值问题有完全通解的充要条件并且通解由(5)给出.

如所周知，当且仅当二次多项式f(x)=ax2+bx+c，a≠0的判别式Δ=b2－4ac大于或等于0时，f(x)才有2实根x±=，并且当a＞0(a＜0)时，x在区间(－∞，x－］∪［x+，∞)(［x－，x+］)上有f(x)≥0.

不难看出:二次多项式3αa33(x)=(2+3λ2+λ3)x2+(2+4λ3)x+2+4λ3有2个不同实根

的充要条件是1+2λ3＜0＜1+2λ2，并且当2+3λ2+λ3＞0时，有u－＜0＜u+;二次多项式3αa12(x) =(2－2λ3)x2+(2－3λ2+λ3)x+2－3λ2+λ3有2不同实根

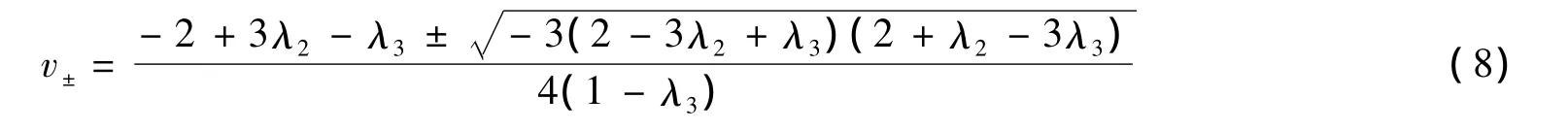
的充要条件是2－3λ2+λ3＜0＜2+λ2－3λ3，并且当2+3λ2+λ3＞0时，有v－＜0＜v+.

定理4以Λ=(1=λ1，λ2，λ3)(1≥λ2≥λ3≥-1)为谱的3阶对称随机矩阵逆特征值问题存在通解的充要条件是

其通解A(x)=S3(x)diag(1，λ2，λ3)ST3(x)由(5)式给出，并且，A(x)的定义域是:当min{1+2λ3，2－3λ2+λ3}≥0时，x∈［0，1］;当1+2λ3≥0和2－3λ2+λ3＜0时，x∈［v+，1］;当1+2λ3＜0和2－3λ2+λ3≥0时，x∈［u+，1］;当1+2λ3＜0和2－3λ2+λ3＜0时，x∈［max{u+，v+}，1］.

证明设A(x)=(aij(x))=S3(x)diag(1，λ2，λ3)ST3(x)，0≤x≤1是以Λ为谱的并由特殊正交矩阵S3(x)决定的、行和全为1的3阶对称矩阵簇(5).对i，j∈{1，2，…，n};x∈［0，1］，以Nij(x)记aij(x)的非负区间，即满足，aij(x)≥0当且仅当x∈Nij(x)，并令Nij=∪0≤x≤1Nij(x).由定理3知: A(x)是以Λ为谱的3阶对称随机矩阵逆特征值问题解的充要条件是x∈Ω=∩1≤i，j≤3Nij.所以，3阶对称随机矩阵逆特征值问题存在通解的充要条件是Ω≠∅，并且当Ω≠∅时其通解可由定义域为Ω的矩阵簇(5)给出.因为Nij(x)=Nji(x)，i，j∈{1，2，3}，x∈［0，1］;同时，由引理1的证明知N22(x)⊆N11(x)N33(x)⊆N11(x)，N12(x)⊆N23(x)⊆N13(x)，x∈［0，1］，所以，Ω=N33∩N12.

若条件(9)不成立，则2+4λ3≤2+λ2+3λ3＜0，在此情况下，如果2+3λ2+λ3＜0，那么按引理1，有3αa33(x)＜0对任意x∈［0，1］成立;如果2+3λ2+λ3＜0，那么3αa33(x)≤(2+3λ2+ λ3)x+(2+4λ3)x+2+4λ3=3(2+λ2+3λ3)＜0对任意x∈［0，1］成立.所以，(9)不成立将蕴含N33=∅，从而Ω=∅，得证条件(9)的必要性.

为证其充分性，只需证明:(9)蕴含Ω≠∅即可.设(9)成立，则1+λ2+λ3≥0.按引理1，若1+2λ3≥0，则N33=［0，1］;若1+2λ3＜0，则1+2λ3＜0≤(2+λ2+3λ3)=1+2λ2，u－＜min {0，u+}从而N33=［0，1］∩(［－∞，u－］∪［u+，∞］)=［u+，1］;若2－3λ2+λ3≥0，则N12=［0，1］;若2－3λ2+λ3＜0，则λ2＞λ3;v－＜min{0，v+}，从而N12=［0，1］∩(［－∞，v－］∪［v+，∞］)=［v+，1］.为了完成本定理的证明，只需证明max{u+，v+}≤1(从而Ω=N33∩N12∈{［0，1］，［u+，1］，［v+， 1］，［max{u+，v+}}非空)即可.事实上，按(7)u+＞1等价于3λ2+λ3，但这是不可能的，因为在条件(9)下，这个不等式等价于下列矛盾式

但这是不可能的，因为，这个不等式等价于下列矛盾式

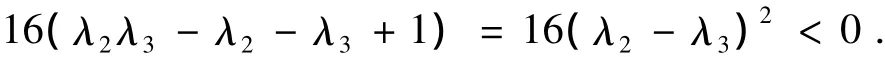
例1因Λ1=(1，0，－0.25)满足定理3的条件(6)，故不存在以它为谱的3阶对称随机矩阵逆特征值问题的完全通解A(x)，其中

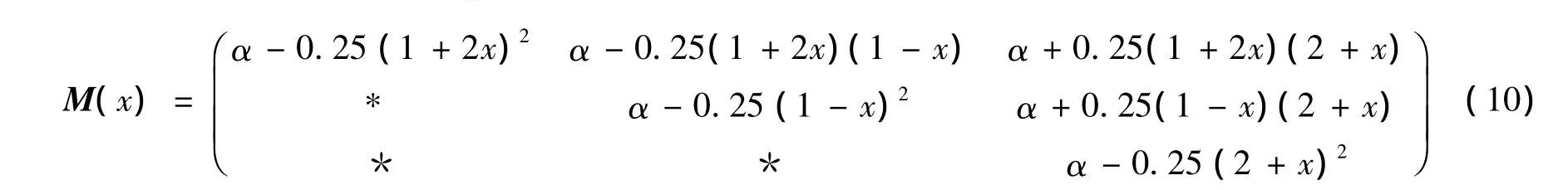
是对称矩阵，α=2(x2+x+1).

因Λ1满足文［12］中定理3.1的条件，从而用该定理的方法可求得一个以Λ1谱的对称随机矩阵是

例2因Λ2=(1，0，－0.6)不满足定理3的条件(6)，故不存在以它为谱的3阶对称随机矩阵逆特征值问题的完全通解.但因Λ1满足文［12］中定理3.1的条件，从而用该定理的方法可求得一个以Λ2谱的对称正随机矩阵是A*此外，Λ2满足条件(6)，从而按定理4，存在以Λ2为谱的3阶对称随机矩阵逆特征值问题的通解.

因1+2λ3＜0≤2+3λ2+λ3，0＜0＜u+==0.535 14＜1，故N33=［u+，1］;因2－3λ2+λ3＞0，故N12=［0，1］.从而，Ω=N33=［0.535 14，1］≠∅.最后求得通解是

值得注意的是:由此通解公式也可推出A(1)=A*是以Λ2为谱的3阶对称随机矩阵.

3 4阶对称随机矩阵逆特征值问题的充分条件

文［12］给出下列几个实质不同的4阶特殊正交矩阵

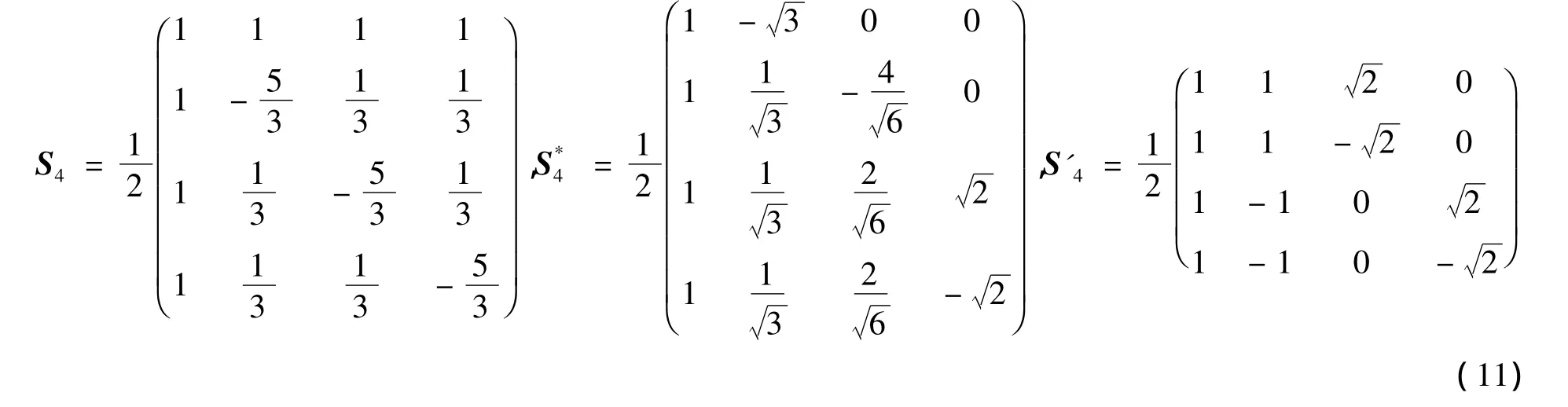
和含1个参数x的4阶特殊正交矩阵簇

利用文［12］的定理5和4阶特殊正交矩阵S*4可推出命题2.

命题2令Λ=(1=λ1，λ2，λ3，λ4)(1≥λ2≥λ3≥λ4≥-1).若

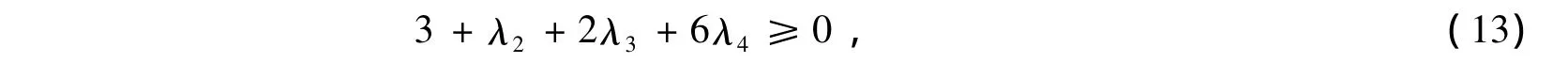
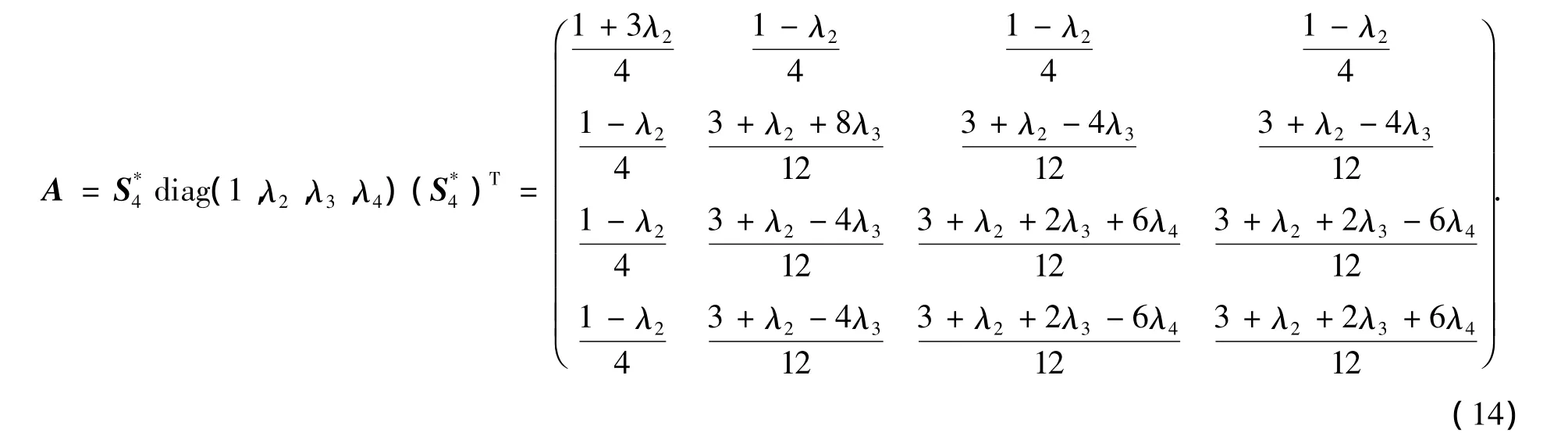
利用文［12］的定理3.2和4阶特殊正交矩阵S4可推出命题3.

命题3令Λ=(1=λ1，λ2，λ3，λ4)(1≥λ2≥λ3≥λ4≥-1)，β=－1)/(n－1).若

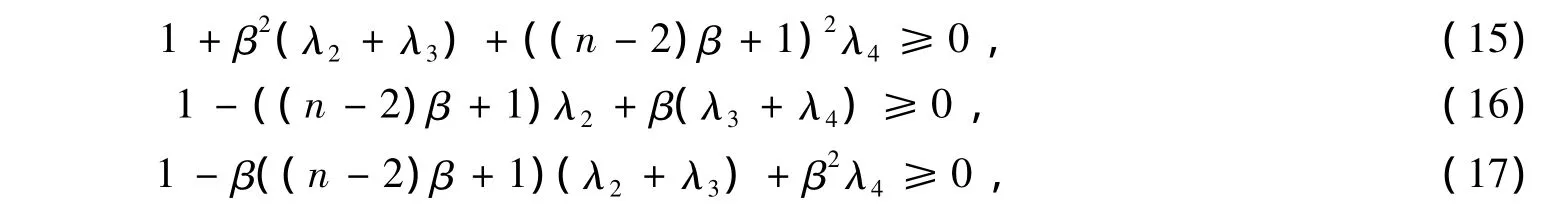
则存在由特殊正交矩阵S4决定的，以Λ为谱的4阶对称随机矩阵

命题4令Λ=(1=λ1，λ2，λ3，λ4)(1≥λ2≥λ3≥λ4≥-1).若

则存在由特殊正交矩阵S'4决定且以Λ为谱的4阶对称随机矩阵

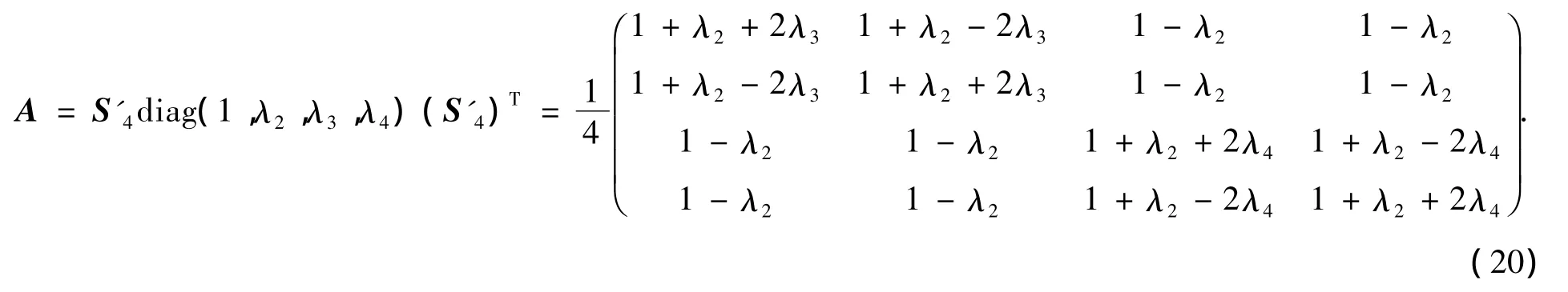
证明按定理1，A=S'4diag(1，λ2，λ3，λ4)(S'4)T以Λ为谱并且行和全为1.注意到1-λ2≥0，1+λ2-2λ4≥0，1+λ2+λ3≥1+λ2+λ4并且当λ4＜0时，1+λ2+λ4≥1+λ2+2λ4;当λ4≥0时，1+λ2+λ4≥0.因此，在条件(19)下，上面以Λ为谱的行和全为1的对称矩阵A是非负矩阵，从而是对称随机矩阵.证毕.

定理5令Λ=(1=λ1，λ2，λ3，λ4)(1≥λ2≥λ3≥λ4≥-1).若

则存在由特殊正交矩阵S4(x)决定含1个参数x且以Λ为谱的4阶对称随机矩阵簇

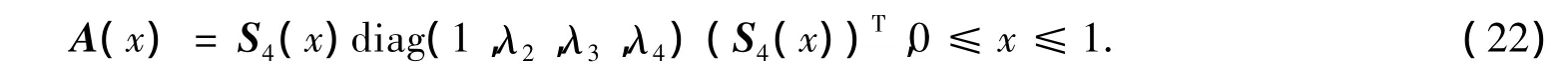
证明按定理1对称矩阵簇(22)的每个矩阵都以Λ为谱并且行和全为1，故只需证明:在条件(19)下对称矩阵簇(22)的每个矩阵都是非负矩阵(随机矩阵)即可.把矩阵簇(22)改写为

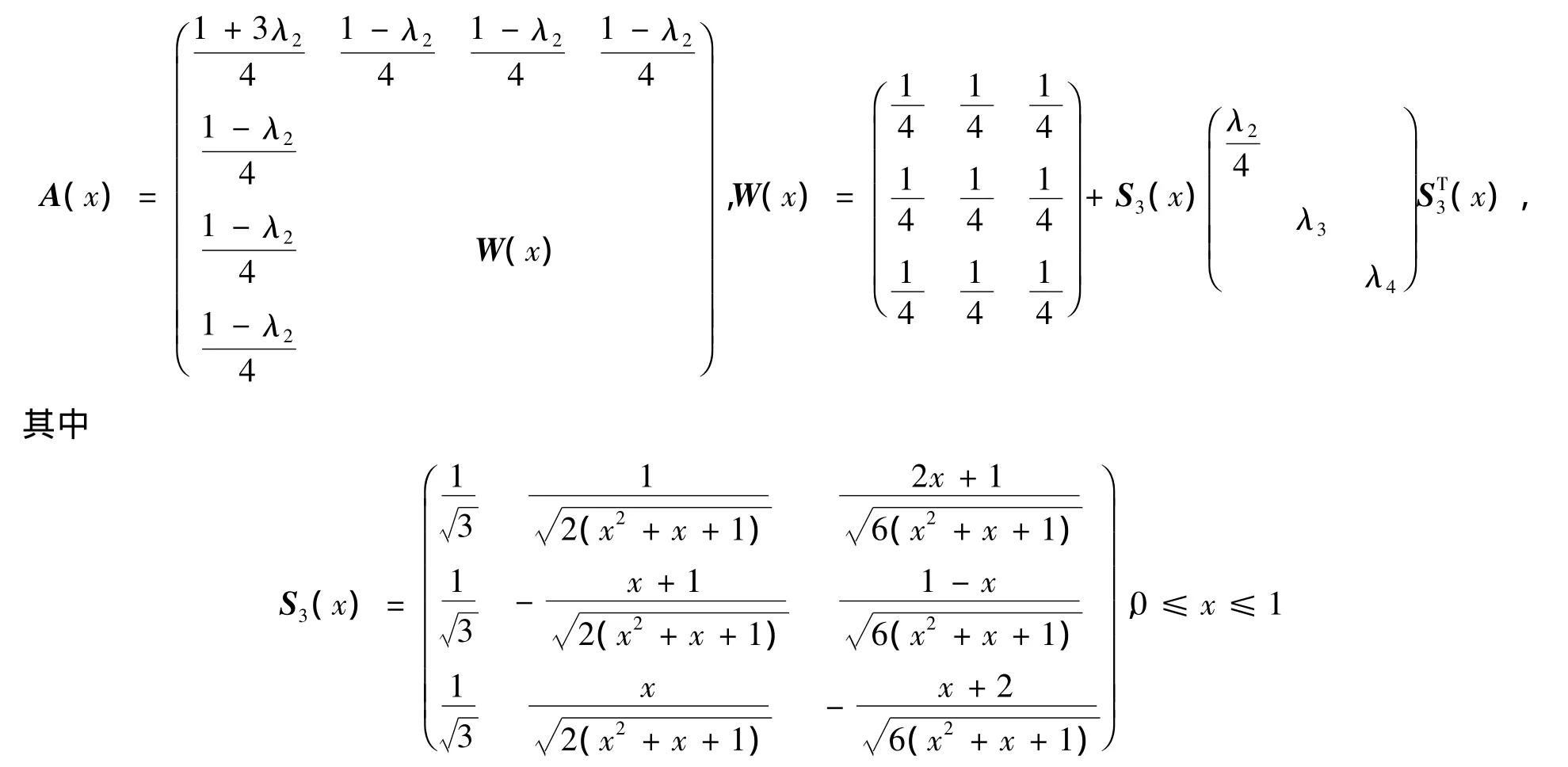
是由(2)定义的含参数x的特殊正交矩阵簇.在条件(21)下，A(x)第1行列的元素全大于等于0.令W(x)=(wij(x))，需要证明:在条件(21)下，对任意x∈［0，1］，i，j=1，…，n，都有wij(x)≥0.令α =2x2+2x+2，则对任意x≥0，都有α＞0.直接计算给出

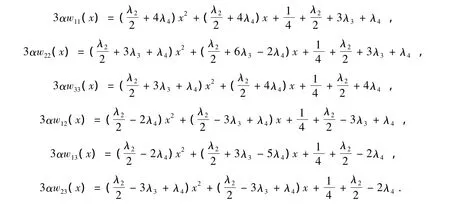
因3α(w11(x)－w33(x))=(3－3x2)(λ3－λ4)≥0，3α(w22(x)－w33(x))=(6x+3)(λ3－λ4)≥0，故min{w11(x)，w22(x)，w33(x)}=w33(x)，0≤x≤1.在条件(21)下，有

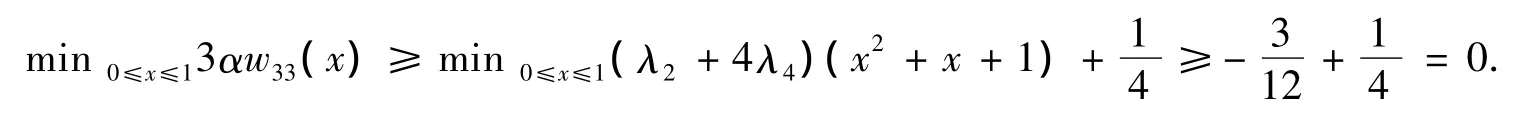
又因3α(w13(x)－w12(x))=3(λ3－λ4)≥0，3α(w23(x)－w12(x))=3(λ3－λ4)(1－x2)≥0，故min{w12(x)，w13(x)，w23(x)}=w12(x)，0≤x≤1.在条件(21)下有

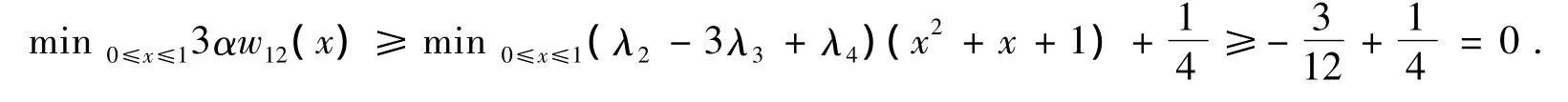
这就证明了:在条件(21)下在闭区间［0，1］上的单参数对称随机矩阵簇(22)的每个矩阵A(x)都以Λ为谱.证毕.

［1］Borobia A.On the nonegative eigenvalue problem［J］.Linear Algebra Appl，1995，223:131－140.

［2］Fiedler M.Eigenvalues of nonnegative symmetricmatrices［J］.Linear Algebra Appl，1974，9:119－142.

［3］Hwang SG，Pyo SS.The inverse eigenvalue problem for symmetric doubly stochastic matrices［J］.Linear Algebra Appl，2004，379:77－83.

［4］Kaddoural C，Mourad B.On a conjecture concerning the inverse eigenvalue problem of 4×4 symmetric doubly stochastic matrices［J］.International Mathematical Forum，2008，31(3):1513－1519.

［5］Mourad B.On a spectrum property of doubly stochastic matrices and its applications to their inverse eigenvalue problem［J］.Linear Algebra Appl，2012，435:3400－3412.

［6］Reams R.An inequality for nonnegativematrices and the inverse eigenvalue problem［J］.Linear Algebra Appl，1996，41:267－375.

［7］Satzman F L.A note on eigenvalues of nonnegativematrices［J］.Linear Algebra Appl，1972，41:329－338.

［8］Soto R，Rojo O.Applications of a Brauer theorem in the nonnegative inverse eigenvalue problem［J］.Linear Algebra Appl，2006，416:844－856.

［9］Yang S，Li X.Inverse eigenvalue problems of 4×4 irreducible nonnegative matrices［C］∥Advances in Matrix Theory and Applications，the proceedings of the Eighth International Conference on Matrix Theory and Applications，World Academic Union，2008.

［10］Yang S，Xu C.Row stochastic inverse eigenvalue problem［J］.Journal of Inequalities and Applications，2011(24):1－5.

［11］杨尚俊.低阶双随机矩阵逆特征值问题［J］.安徽大学学报:自然科学版，2013，37(2):1－7.

［12］杨尚俊.对称双随机矩阵逆特征值问题［J］.安徽大学学报:自然科学版，2013，37(6):1－7.

(责任编辑 朱夜明)

On the inverse eigenvalue problem for symmetric doubly stochastic matrices of order two to four

YANG Shang－jun
(School of Mathematical Science，Anhui University，Hefei 230039，China)

Given an n－tupleΛof numbers，real or complex，the problem of deciding the existence of a nonnegative(stochastic)matrix with spectrumΛis called the nonnegative(stochastic)inverse eigenvalue problem.This problem has long time been one of the problems ofmain interest in the theory of matrices.Other reference gave the sufficient conditions for doubly stochastic inverse eigenvalue problem of order two to five to have a solution and the formulas of the corresponding solution，and firstly gave the sufficient conditions for constant row sums symmetric inverse eigenvalue problem(of any order)to have a solution and the formula of corresponding solution，and then gave the sufficient conditions for the symmetric stochastic inverse eigenvalue problem to have a solution and the corresponding solution.In this paper，after presenting the concept of general solution of an inverse eigenvalue problem(of any order)and the concept of totally general solution of a 3×3 symmetric doubly stochastic inverse eigenvalue problem，we firstly gave the sufficient and necessary conditions for a 3×3 symmetric doubly stochastic inverse eigenvalue problem to had the totally general solution with the formula of the totally general solution，secondly gave the sufficient and necessary conditions for a 3×3 symmetric doubly stochastic inverse eigenvalue problem to had thegeneral solution with the formula of the totally general solution，and finally gave several sufficient conditions for a 4×4 symmetric doubly stochastic inverse eigenvalue problem to had a solution with the formula of the general solution.

general solution of an inverse eigenvalue problem;symmetric doubly stochastic inverse eigenvalue problem;typical orthogonalmatrix

O151.2

A

1000－2162(2014)04－0001－08

10.3969/j.issn.1000－2162.2014.04.001

2014－01－02

安徽大学创新团队基金资助项目(KJTD001B)

杨尚俊(1937—)，男，贵州贞丰人，安徽大学教授，硕士生导师.