修正矩阵Drazin逆的表示

崔润卿，李幸兰，2

(1.河南理工大学数学与信息科学学院，河南焦作454003;2.中国矿业大学银川学院基础课部，宁夏银川750011)

修正矩阵Drazin逆的表示

崔润卿1，李幸兰1，2

(1.河南理工大学数学与信息科学学院，河南焦作454003;2.中国矿业大学银川学院基础课部，宁夏银川750011)

以往文献给出了类似Sherman－Morrison－Woodbury式的修正矩阵Drazin逆的表达式及基于广义Schur补的修正矩阵Drazin逆的表达式.论文在上述结果的基础上，给出了另外一组不同的条件求得了修正矩阵Drazin逆的表达式，其表达式与上述结果相似，同时补充了群逆的情况.

Drazin逆;修正矩阵;广义Schur补;幂零

广义逆作为矩阵论的一个重要分支及其在工程计算上面的广泛应用，近几十年来一直是矩阵论领域研究的热点问题之一［1－14］，而Drazin逆作为广义逆中独特的一份子也得到了长足的发展［1－9］.

Drazin逆在微分方程、自动化、数值分析等诸多领域扮演着重要的角色，具有广泛的应用.目前对于Drazin逆的研究主要包含Drazin逆的表示、Drazin逆的扰动边界等，且已发展到不同的代数空间上.修正矩阵是在一个基矩阵基础上的扰动矩阵(或称误差矩阵)，它在统计学领域有着广泛的应用.

一个关于求逆的众所周知的Sherman－Morrison－Woodbury式为

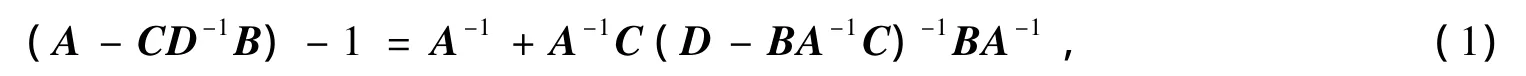
这里矩阵A、D和Schur补D－BA－1C都是可逆的.这个式子已经在MP广义逆中得到推广，并在Drazin逆和加权广义逆中的推广得到了研究.研究这个问题的学者从不同方面进行研究，一部分通过研究广义Schur补非奇异或等于零时修正矩阵Drazin逆的表示［2－7］，另一部分研究更为广泛的例子即广义Schur补不需要证明非奇异或等于零时修正矩阵Drazin逆的表示［8－9］.

1 主要结果及证明

设A∈Cn×n，其中Cn×n为全体n阶复矩阵集合.考虑矩阵序列A1，A2，A3，…，Ak，Ak+1，…，有rank (Ak+1)=rank(Ak).A的指数ind(A)定义为使等式

成立的最小非负整数k.

定义1设A∈Cn×n，其指数ind(A)=k，若方阵X满足

则称X为A的Drazin逆，记作AD.特别地，当k=1时，AD称为A的群逆，记作A#.并记

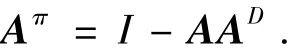
性质1 ADAπ=AπAD=0，AAπ=AπA，(Aπ)2=Aπ.

定理1设A，B，C，D∈Cn×n，ind(A)=k，Z=D－BADC，若

(1)DZD+Zπ=0;

(2)BAπ=0;

(3)(A－CDDB)AD=AD(A－CDDB);

(4)AADC－CDDD+CDDZ=0;

(5)BAAD+DDDB－ZDDB=0.

则

此外，有

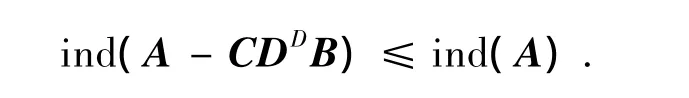
证明令X为式(2)的右边，先证明

因为

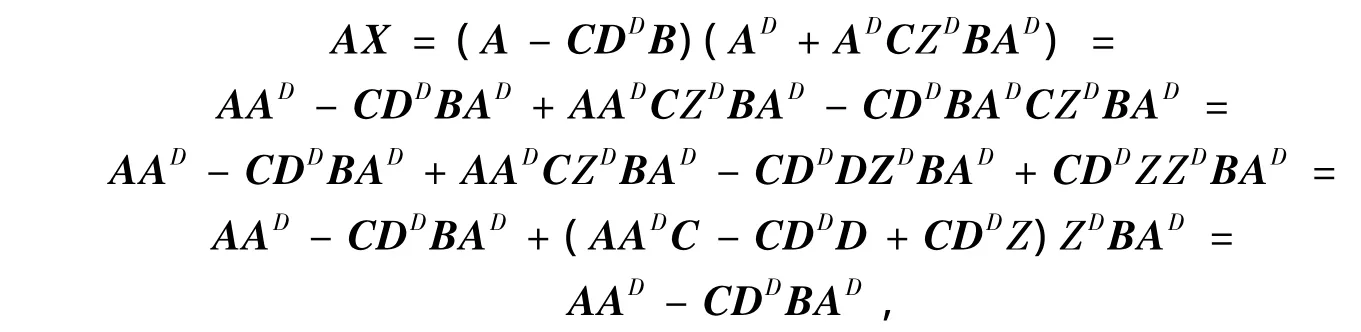
上式证明过程中用到了定理1中的条件(4)，且

则证明了

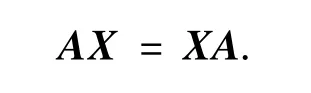
下面证明

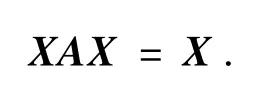
因为

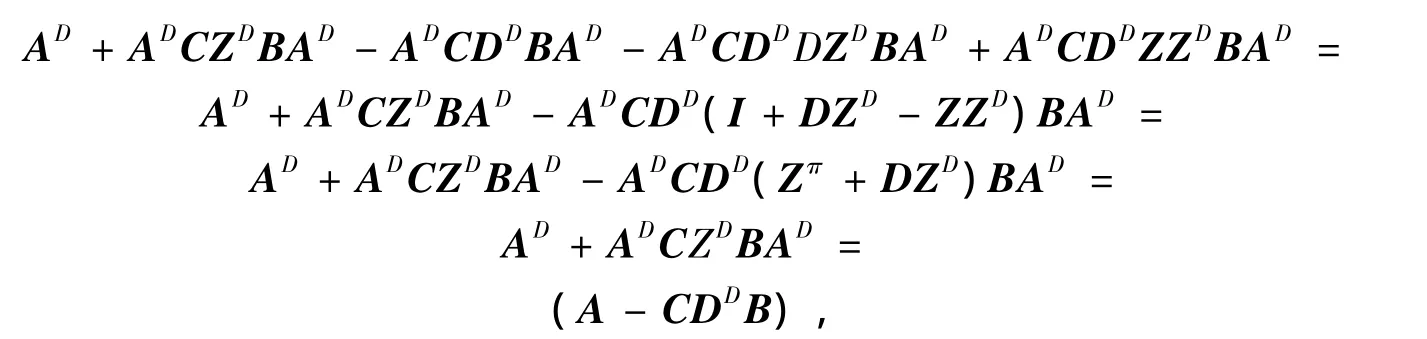
则XAX=X证明完毕.

下面证明

因为

AkXA=Ak与A－A2X幂零等价，所以证明A－A2X幂零即可.

因为

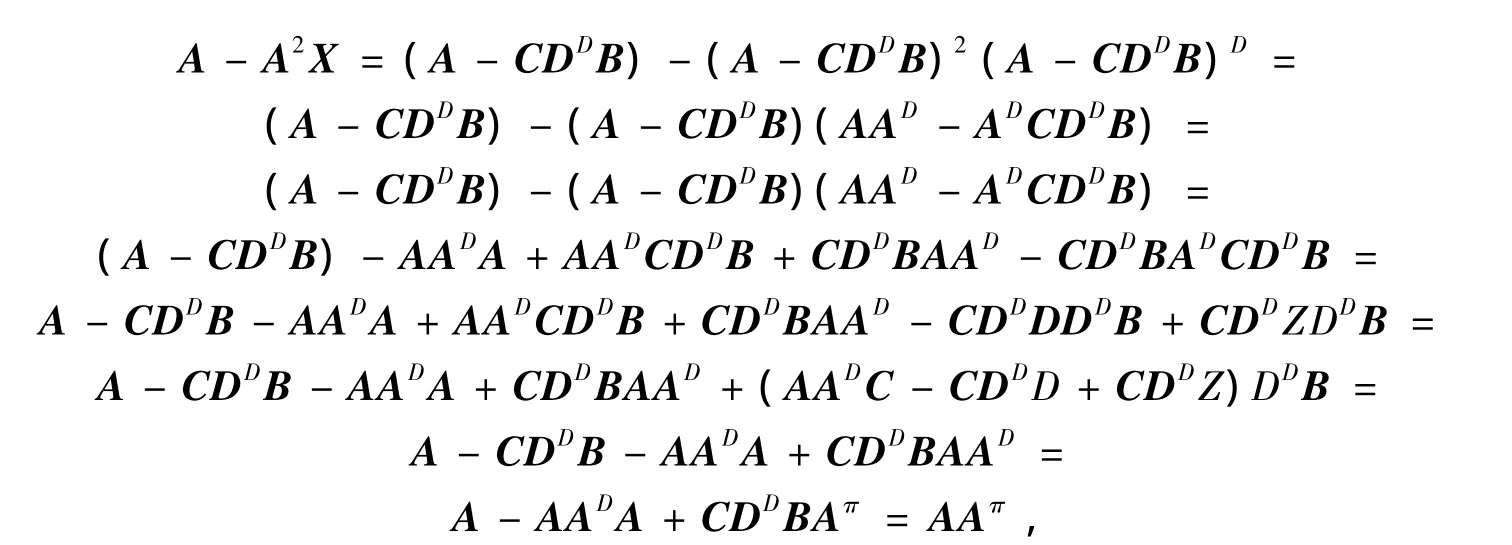
则

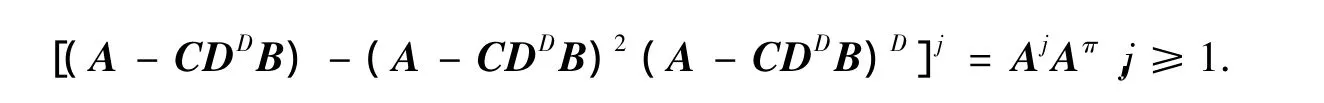
又因为

所以(A－CDDB)－(A－CDDB)2(A－CDDB)D是幂零的，且

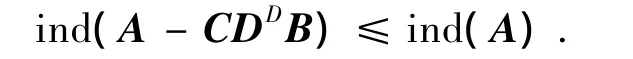
推论1设A，B，C∈Cn×n，ind(A)=k，Z=I－BADC，若

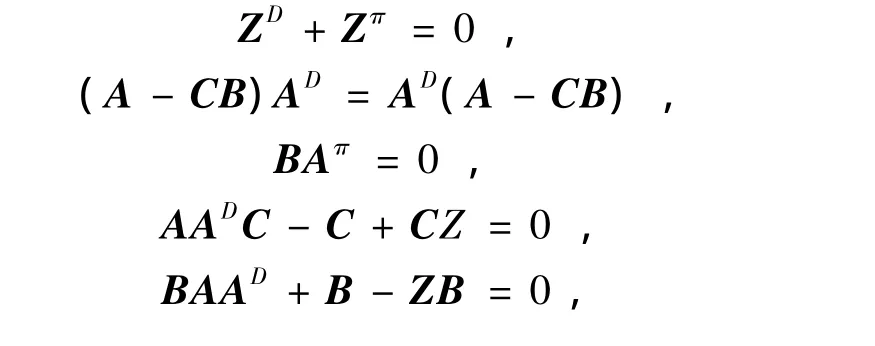
则

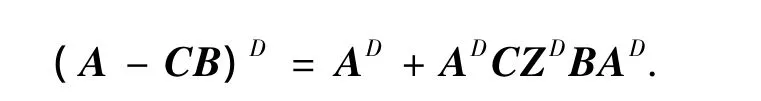
此外，有

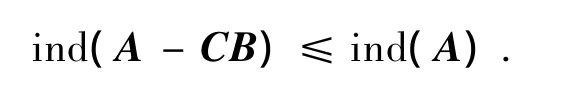
推论2设A，B，C∈Cn×n，ind(A)=k，Z=I－BADC，若

则

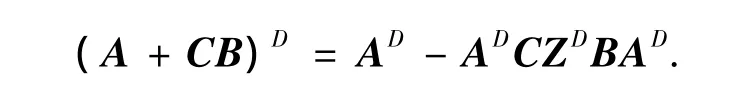
此外，有

推论3在推论1、2的条件下，若ind(A)=1，则A有群逆A#且有ind(A－CB)=1，因此有

推论4设A，B∈Cn×n，ind(A)=k，Z=I－BAD，若

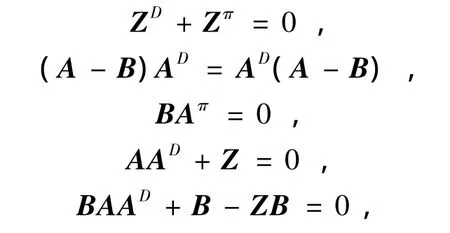
则

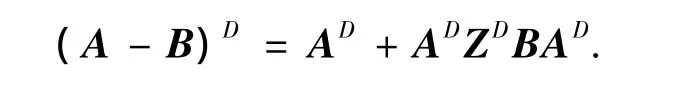
此外，有

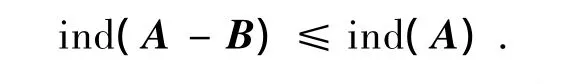
这几个推论给出了修正矩阵另外两种形式下的Drazin逆的情况.

［1］Dopazo E，Martínez－Serrano M F.On deriving the Drazin inverse of a modified matrix［J］.Linear Algebre Appl，2011，in press.

［2］Wei Y M.The Drazin inverse of amodified matrix［J］.Applied Mathematics and Computation，2002，125:295－301.

［3］Cvetkovic'－Ilic'D S，Wei Y.Representations for the Drazin inverse ofbounded operators on Banach space［J］.Electron Linear Algebra，2009，18:613－627.

［4］Hartwig R E，Li X，Wei Y.Representations for the Drazin inverse of 2×2 block matrix［J］.Matrix Anal Appl，2006，27:757－771.

［5］Martínez－Serrano M F，Castro－González N.On the Drazin inverse of block matrices and generalized Schur complement［J］.Appl Math Comput，2009，215:2733－2740.

［6］Wei Y.Expressions for the Drazin inverse of a 2×2 block matrix［J］.Linear and Multi Linear Algebra，1998，45: 131－146.

［7］Wei Y.The Drazin inverse of updating of a square matrix with application to perturbation formula［J］.Appl Math Comput，2000，18:77－83.

［8］Deng C Y.On the invertibility of the operator A－XB Numer［J］.Linear Algebra Appl，2009，16:817－831.

［9］Hartwig R E，Wang G，Wei Y.Some additive results on the Drazin inverse［J］.Linear Algebra Appl，2001，322: 207－217.

［10］Wang G Y，Wei Y M，Qiao SZ.Generalized inverse:theory and computations［M］.Beijing:Science Press，2006: 251－254.

［11］乔三正.Banach空间中线性算子的Drazin逆［J］.上海师范学院学报:自然科学版，1981(2):11－18.

［12］程云鹏.矩阵论［M］.西安:西北工业大学出版社，2002:353－360.

［13］侯双根，李洪昌.关于广义逆矩阵A～的两个计算公式［J］.河南理工大学学报:自然科学版，1992(3): 73－76.

［14］王松桂.广义逆矩阵及其应用［M］.北京:北京工业大学出版社，1996:31－36.

(责任编辑 朱夜明)

Representations of the Drazin inverse of a modified matrix

CUIRun－qing1，LIXing－lan1，2
(1.School of Mathematics and Information Science，Henan Polytechnic University，Jiaozuo 454003，China; 2.Department of Basic，China University of Mining and Technology Yinchuan College，Yinchuan 750011，China)

The representations of the Sherman－Morrison－Woodbury for the Drazin inverse of a modified matrix and the representations of a modified matrix through the generalized Schur complement have been given in other papers.In this paper，we extended those results，and gave another different condition to get representations for the Drazin inverse of amodified matrix，and the representations were similar to results above.At last，we supplement the situation of the group inverse.

Drazin inverse;modified matrix;generalized Schur complement;niplotent

O151.21

A

1000－2162(2014)04－0009－04

10.3969/j.issn.1000－2162.2014.04.002

2013－12－15

河南省高等教育教学改革研究省级立项项目(2012SJGLX125)

崔润卿(1966—)，男，河南偃师人，河南理工大学副教授.