点群的复表示环之增广商群

常山

(合肥工业大学数学学院，安徽合肥230009)

点群的复表示环之增广商群

常山

(合肥工业大学数学学院，安徽合肥230009)

设G是有限群，R(G)为G的复表示环，I(G)为其增广理想.对第一类点群(特殊正交群SO3(R)的有限子群)和任意的自然数n，给出了增广理想的n次幂In(G)作为自由交换群的基底，并确定了其增广商群In(G)/In+1(G)的结构.

点群;复表示环;增广商群

设G是有限群，G的一个复矩阵表示(以下简称表示)是指群同态

其中:GLd(C)是d阶复一般线性群，正整数d为表示p的维数.G的两个表示p和q称为是等价的，如果存在可逆方阵K，使得

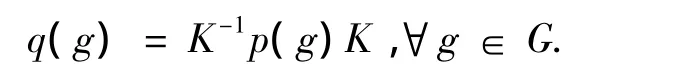
记表示p，q的等价类为［p］，［q］，定义加法［p］+［q］=［p⊕q］，其中

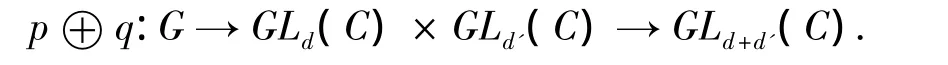
可以证明，G的所有表示的同构类组成的集合在如上定义的加法下构成一个交换半群，该交换半群的群完备化即为G的复表示环R(G)，其加法和乘法分别由矩阵的直和和张量积诱导.由文［1］可知，R(G)是一个含单位元的交换环，其加法群是以G的所有不可约表示的等价类为基底的自由交换群，秩等于G的共轭类的个数.

表示的维数诱导了R(G)上的一个典范环同态

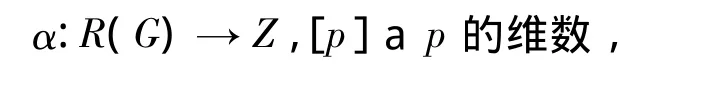
称为R(G)的增广映射，α的核I(G)称为R(G)的增广理想.记I(G)的n次幂为In(G)，称

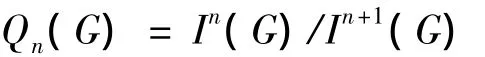
为R(G)的第n个增广商群.

确定In(G)和Qn(G)的结构是代数表示理论中一个十分有意义的课题.在文［2－3］中，作者对二面体群Dm给出了In(Dm)作为自由交换群的一组基底并完全确定了Qn(Dm)的结构.此外，作者还证明了对任意的有限交换群G，有

其中:Δ(G)是G的整群环ZG的增广理想.

Karpilovsky在文［4］中提出了如下公开问题:对任意的有限群G和所有的正整数n，确定商群Δn(G)/Δn+1(G)的结构和同构分类.关于这个公开问题已有许多的文献进行了研究，如文［5－8］.值得一提的是，作者和唐国平在文［8］中对任意的有限交换群彻底解决了这个公开问题，从而对任意有限交换群G确定了Qn(G)的结构.

第一类点群是特殊正交群SO3(R)有限子群，包括有限循环群、二面体群、正四面体群T、正八面体群O和正二十面体群I.论文对任意正整数n，给出了T，O，I的复表示环的增广理想的n次幂作为自由交换群的一组基底，并完全确定了其增广商群的结构.因为T，O，I分别同构于A4，S4，A5，所以论文的结果同时确定了Qn(A4)，Qn(S4)，Qn(A5)的结构，这里Am和Sm分别表示m元的交错群和对称群.

1 预备知识

本节列出若干关于Qn(G)和有限生成自由交换群的已知结果.

定理1［3］对任意的正整数n，Qn(G)是有限交换|G|－扭群.

推论1［3］设G的共轭类个数为c(G)，则对每个正整数n，In(G)都是秩为c(G)－1的自由交换群.

引理1［9］设H是秩为N的自由交换群，如果H中有N个元生成H，则这N个元组成H的基底.

有限群表示论中的一个经典结果是两个表示等价当且仅当它们的特征标相等，表示的特征标诱导单同态

f将表示的同构类［p］映到p的特征标

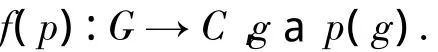
特征标在G的共轭类上不变，因此用表1刻画G的所有不可约表示的同构类.其中:c1={1}，c2，…，cr是G的所有共轭类;［p1］，［p2］，…，［pr］是G的所有不可约表示的同构类;fi是pi的特征标.特别地，［p1］是G的平凡表示，di=fi(1)是pi的维数.

表1 G的特征标表Tab.1 Character table of G

约定如下记号:若gi∈ci，则用gi代表共轭类ci;设S是R(G)的子集，用ZS表示S中元的所有整系数线性组合组成的集合;用Cm表示m阶循环群.

2 Qn(T)的结构

由文［10］可得正四面体群T(或A4)的特征标表，如表2所示.其中

表2 T的特征标表Tab.2 Character table of T

由此可得R(T)的乘法表，如表3所示.

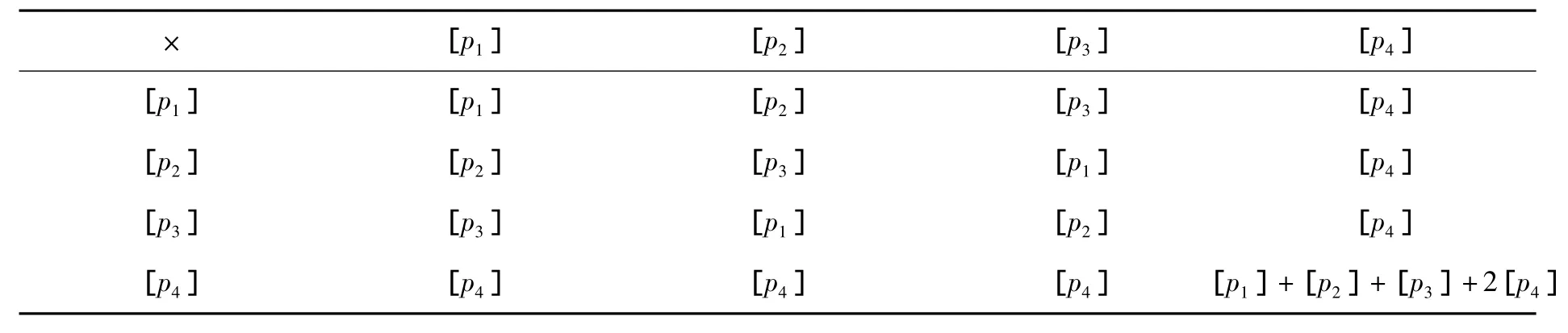
表3 R(T)的乘法表Tab.3 M ultiplication table of R(T)

引理2设E=［p1］－［p2］，F=［p1］－［p3］，X=［p1］+［p2］+［p3］－［p4］，则

(1)I(T)是以{E，F，X}为基底的自由交换群;

(2)EX=0，FX=0，E2=2E－F，F2=2F－E，EF=E2+F2=E+F，X2=4X.

证明(1)由推论1和表2可知I(T)的秩为3，因此仅需证明{E，F，X}生成I(T).令

则a1+a2+a3+3a4=0.易见

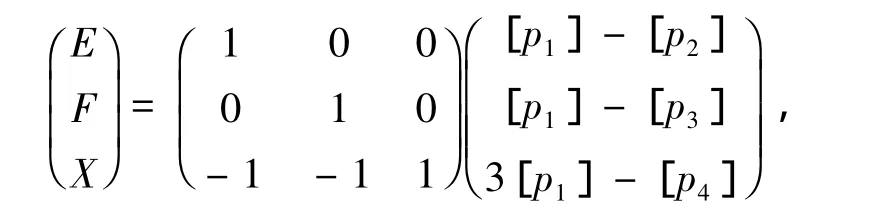
于是

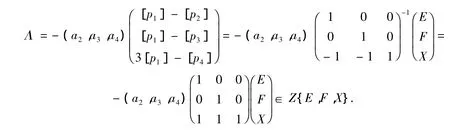
(2)由表3计算即得.

定理2对任意的正整数n，In(T)是以{En，En－1F，Xn}为基底的自由交换群.

证明仅需(1)生成In(T).根据引理2，In(T)可由{En，En－1F，…，Fn，Xn}生成.在等式F2=EFE2的两侧依次乘以Fn－2，EFn－3，…，En－2可得

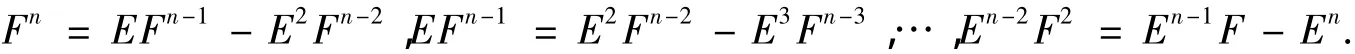
定理3对任意的正整数n，Qn(T)≌C3⊕C4.

证明对任意正整数n，由定理2和引理2可得

In+1(T)=Z{En+1，EnF，Xn+1}=Z{2En－En－1F，En+En－1F，4Xn}=Z{3En，En+En－1F，4Xn}.

易见{En，En+En－1F，Xn}也是In(T)的一组基底，于是

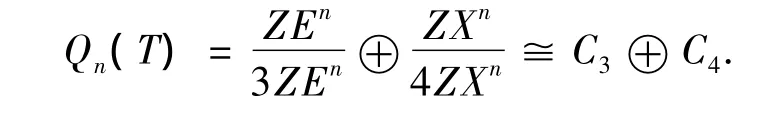
3 Qn(O)的结构

由文［9］可得正四面体群O(或S4)的特征标表，如表4所示.

表4 O的特征标表Tab.4 Character table of O

由此可得R(O)的乘法表，如表5所示.

表5 R(O)的乘法表Tab.5 M ultiplication table of R(O)

引理3设E=［p1］－［p2］，F=［p4］－［p5］，X=［p1］+［p3］－［p4］，Y=［p1］+［p2］－［p3］.那么

(1)I(O)是以{E，F，X，Y}为基底的自由交换群;

(2)EY=FY=XY=0，EX=FX=E+F，E2=F2=2E，EF=2F，X2=4X－E－F，Y2=3Y.

证明(1)根据推论1和表4，I(O)的秩为4，因此仅需证明{E，F，X，Y}生成I(O).令

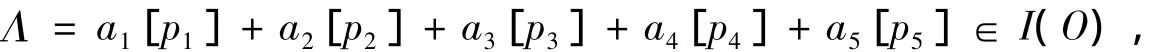
则a1+a2+2a3+3a4+3a5=0.计算可得

于是

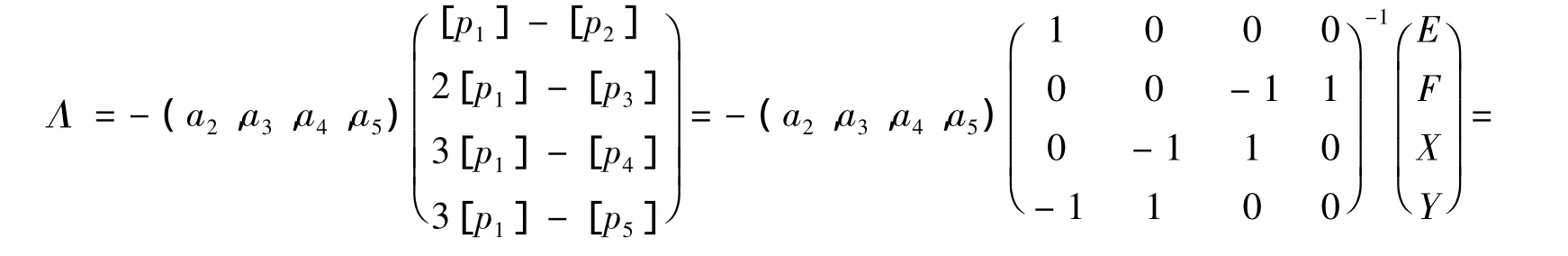
(2)由表5计算即得.

定理4对任意的n≥2，In(O)是以{En，En－1X，Xn，Yn}为基底的自由交换群.

证明易见仅需证明对任意的n≥2，(20)生成In(O).由等式EY=FY=XY=0和EX=FX可知

是In(O)的一个生成元集.由E2=F2可得

再由EX2=(E+F)X=2EX=E2X，得

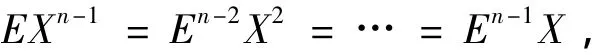
于是In(O)可由{En，En－1F，En－1X，Xn，Yn}生成.最后，由引理3计算可知En－1X=En－1+En－2F，从而

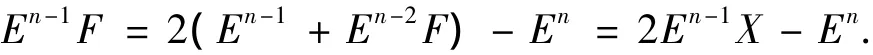
由文［9］可得正二十面体群I(或A5)的特征标表，如表6所示.

证明首先计算Q1(O).由定理4可得

另一方面，{E，E+F，X，Y}显然也是I(O)的基底，于是

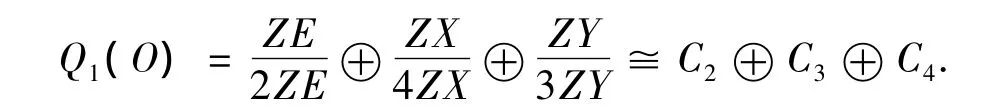
设n≥2，计算可得

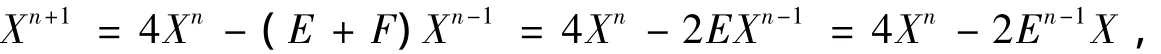
从而

因此，由定理4可知对任意的n≥2，有

4 Qn(I)的结构

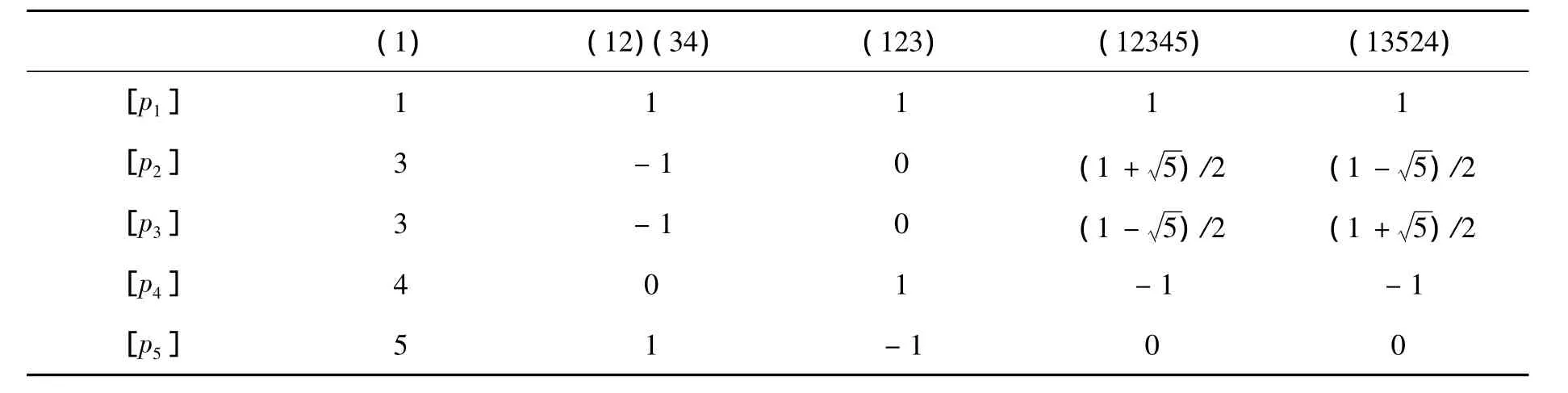
表6 I的特征标表Tab.6 Character table of I

由此可得R(I)的乘法表，如表7所示.其中:∑=［p1］+［p2］+［p3］+［p4］+［p5］.

表7 R(I)的乘法表Tab.7 Multiplication table of R(I)

引理4设E=［p1］+［p2］－［p4］，F=［p1］+［p3］－［p4］，X=［p1］－［p2］－［p3］+［p5］，Y =［p1］+［p4］－［p5］，则

(1)I(I)是以{E，F，X，Y}为基底的自由交换群;

(2)EY=FY=XY=0，EX=FX=0，E2+F2=3EF，E2=4E－F，EF=E+F，X2=4X，Y2=3Y.

证明(1)由推论1和表6可知I(I)的秩为4，因此仅需证明{E，F，X，Y}生成I(I).令

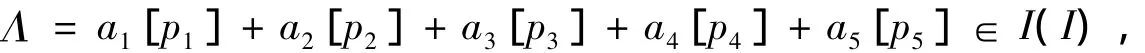
则a1+3a2+3a3+4a4+5a5=0.计算可得

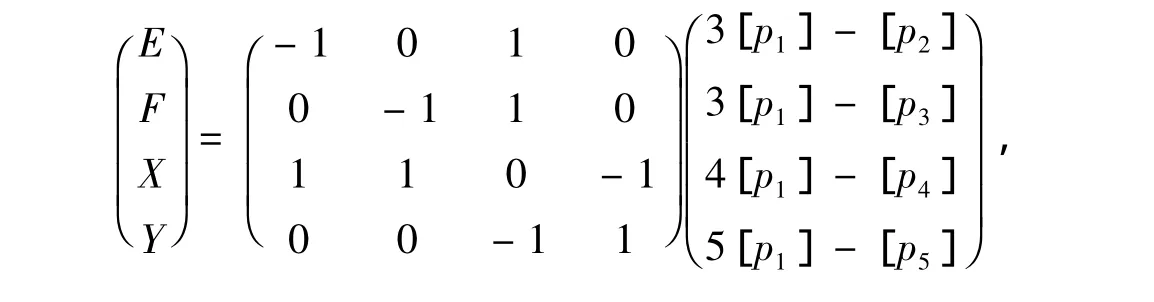
于是

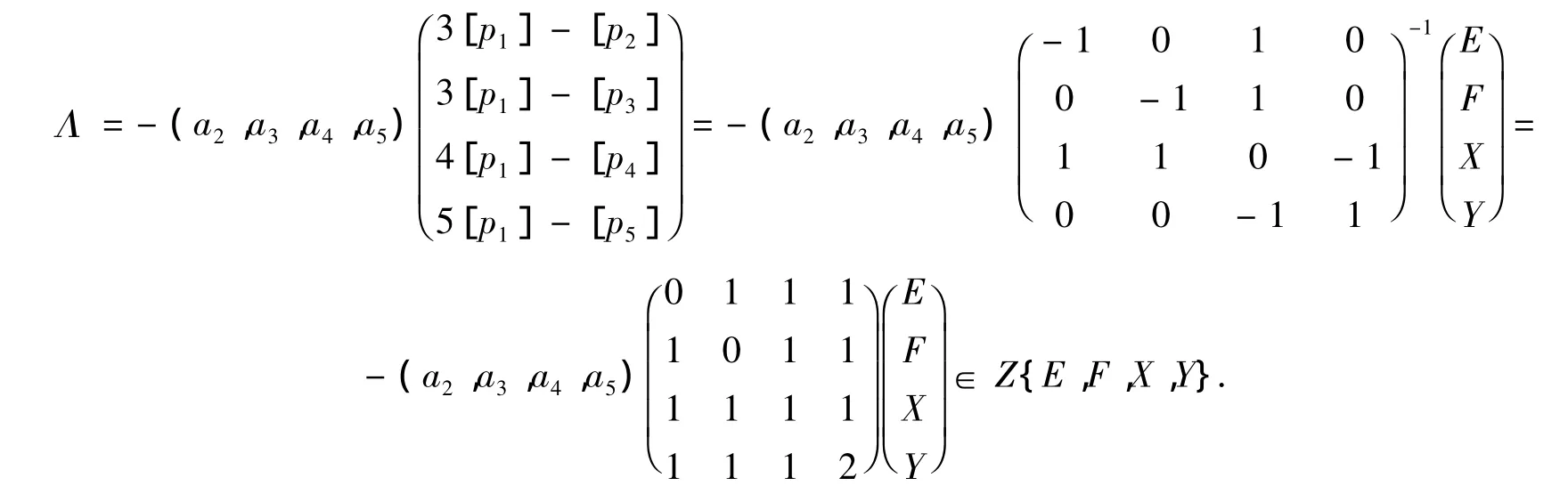
(2)由表7计算即得.

定理6对任意的正整数n，In(I)是以{En，En－1F，Xn，Yn}为基底的自由交换群.

证明由引理4，仅需对n≥2证明.由等式EY=FY=XY=0和EX=FX=0，可知In(I)可由

生成.在等式F2=3EF－E2的两侧依次乘以Fn－2，EFn－3，…，Fn－2可得

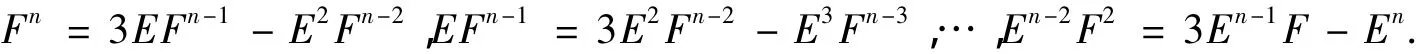
定理7对任意的正整数n，Qn(I)≌C3⊕C4⊕C5.

证明对任意的正整数n，由定理6和引理4可得

另一方面，易见{En，En+En－1F，Xn，Yn}也是In(I)的基底，因此，对任意的正整数n，有

5 关于Qn(Am)结构的猜想

注意到A3是交换群，且A3≌C3，于是由文［3］和［8］可得

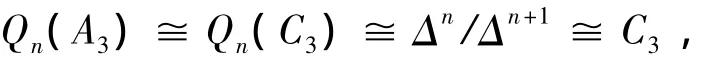
结合定理3和定理7，猜测对任意的m≥3和任意的正整数n，有

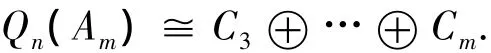
［1］Magurn B A.An algebraic introduction to K－theory［M］.Combridge:Combridge University Press，2002:252－277.

［2］Fulton W，Harris J.Representation theory:a first course［M］.New York:Springer－Verlag，1991:12－18.

［3］Chang S，Chen H，Tang G P.Augmentation quotients for complex representation rings of dihedral groups［J］.Front Math China，2012，7(1):1－18.

［4］Karpilovsky G.Commutative group algebras［M］.Michigan:Marcel Dekker，1983:202－211.

［5］Hales AW.Stable augmentation quotients of abelian groups［J］.Pacific JMath，1985，118(2):401－410.

［6］Tang G P.On a problem of Karpilovsky［J］.Algebra Colloq，2003，10(1):11－16.

［7］Tang G P.Structure ofaugmentation quotients of finite homocyclic abelian groups［J］.SciChina Ser A，2007，50(7): 1280－1288.

［8］Chang S，Tang G P.A basis for augmentation quotients of finite abelian groups［J］.JAlgebra，2011，327(1):466－488.

［9］Lang S.Algebra［M］.3rd ed.New York:Springer，2002:42－47.

［10］孟道骥，朱萍.有限群表示论［M］.北京:科学出版社，2006:56－81.

(责任编辑 朱夜明)

Augmentation quotients for com plex representation rings of point groups

CHANG Shan
(School of Mathematics，Hefei University of Technology，Hefei 230009，China)

Let G be a finite group，R(G)its complex representation ring，and I(G)its augmentation ideal.This paper obtained an explicit Z－basis of In(G)and determined the isomorphism class of the n－th augmentation quotient In(G)/In+1(G)for the first type of pointgroup(i.e.finite subgroup of the special orthogonal group SO3(R))and for each positive integer n.

point group;complex representation ring;augmentation quotient

O153

A

1000－2162(2014)04－0013－07

10.3969/j.issn.1000－2162.2014.04.003

2014－02－21

国家自然科学基金天元专项(11226066);安徽省自然科学基金青年项目(1308085QA01)

常山(1983—)，男，安徽合肥人，合肥工业大学讲师，中国科学技术大学博士后.