编队构型最优开关控制策略研究
陈祥, 廖鹤, 童庆为, 宋涛
(上海卫星工程研究所 研发中心, 上海 200240)
0 引言
卫星编队可以形成大的口径或测量基线,在电子侦察、立体成像、精确定位、气象测量等方面具有很大的优势,是当前航天领域的重要研究方向[1]。卫星编队长期在轨运行中要求进行构型保持或重构,以满足任务需求。根据任务要求,一般可以分为时间最短控制和燃料最省控制。
目前编队构型的控制研究主要集中于燃料最省策略研究,控制方式按照推进方式可以分为脉冲控制和连续推力控制。德国TanDEM-X卫星任务采用面内双脉冲、面外单脉冲的简单控制策略,该策略并不是最优的,会造成编队构型速度方向漂移,从而导致控制频繁,构型容易发散[2]。四脉冲控制策略作为经典的最优编队构型控制策略,具有求解简单的优点,与双脉冲策略相比,速度方向不发散,且燃料消耗也相对较优[3]。还有一些学者针对脉冲编队构型控制问题,设计了LQR控制策略和基于Lyapunov方法[4]的控制策略,但燃料消耗较前两种策略更多。基于有限推力或连续推力方法进行编队构型控制研究的思路是:基于Hill方程进行最优控制建模后通过优化算法求解得到最优控制问题的解。该思路经典直观,但是存在计算量大,不易求解等缺陷[5-6]。
本文针对编队飞行的连续小推力最优控制问题,根据编队飞行的运动特点,采用最优控制理论和极小值原理设计了仅需要求解非线性方程组的编队构型的最短时间和最省燃料开关控制策略,并进行数值仿真,验证了控制策略的正确性和优越性。
1 动力学模型
首先定义目标轨道坐标系:Oe为地心,坐标原点O位于目标星的质心,Ox轴沿目标星地心距矢量方向,Oy轴指向速度方向,Oz轴与Ox轴和Oy轴组成右手坐标系。目标轨道坐标系如图1所示。
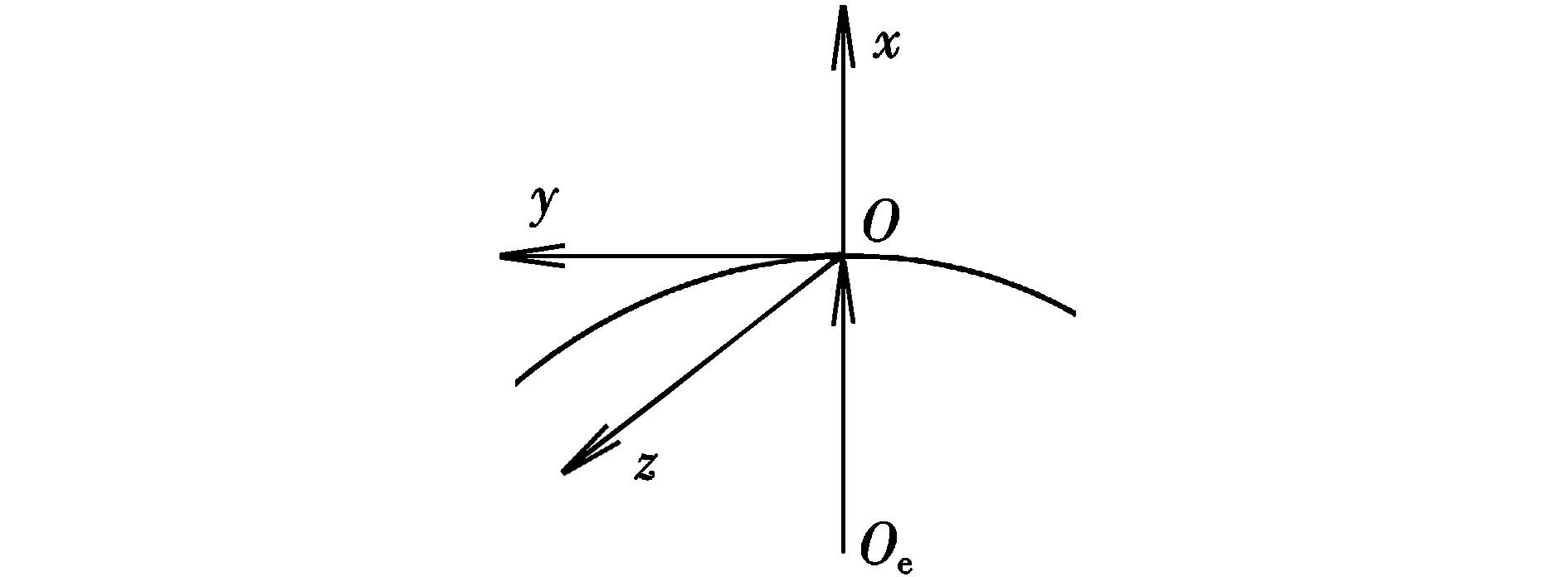
图1 目标星轨道坐标系Fig.1 Target satellite orbital coordinate system
在目标轨道坐标系中满足目标轨道为圆轨道和近距离假设条件时,编队飞行的跟随航天器相对目标航天器的运动可表示为Hill方程[7],即编队构型控制状态方程:
(1)
将式(1)改写为状态转移矩阵形式如下:
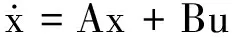
(2)
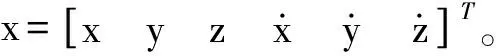
x(t)=Φ(t)x(0)+Γ(t)u
(3)
式中,Φ(t)为状态转移矩阵;Γ(t)为控制响应矩阵。为得到全局最优解,Hill方程改写为[2]:
(4)
式中,R为相对运动在轨道平面内分运动的短半轴;S为平面外简谐振动的振幅;nt为t时刻目标星的平纬度幅角;θ0为跟随航天器在目标轨道平面内运动的初始相位;φ0为简谐振动的初始相位。
2 最优构型控制策略
由于编队飞行相对运动在目标星轨道平面内和轨道平面外的运动是解耦的,因此,分别进行编队飞行的轨道面内控制和面外控制,再通过约束条件将两项运动结合,即可得到控制问题的解。
2.1 时间最短开关控制策略
根据最优控制原理,式(2)线性定常系统的最短时间机动问题即为终端时间自由的状态转移问题,最优控制为Bang-Bang控制[8],控制切换流程如图2所示。图中,t1,t2,t3,tf,tz1和tzf为待优化变量。
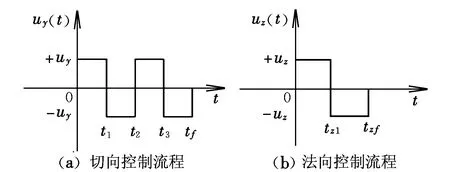
图2 时间最短控制切换流程Fig.2 Switching sequence for minimum-time control
时间最短控制的性能指标为:

(5)
哈密尔顿函数为:
Htime(t)=1+λT(t)[Ax(t)+Bu(t)]
(6)
协态方程为:
(7)
极值条件为:
H[x*(t),u*(t),λ(t),t]=
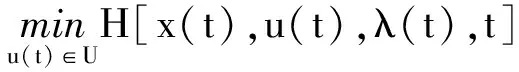
(8)
根据最优控制原理,定常系统时间最短控制的哈密尔顿函数须保持为0,并满足式(8)极值条件。根据最优控制原理,式(8)等价为:
λT(ti)B=0,∀ti
(9)
式中,λT(ti)B定义为切换函数;ti为Bang-Bang控制切换的时刻。根据图2可知,在初始和终端构型条件已知时,式(3)可以转化为式(10)和式(11)。求解式(10)和式(11)即可得到时间最短控制对应的控制切换时刻和终端时间。
(10)
(11)
式中,uy0为Oy轴方向输入的控制加速度;uz0为Oz轴方向输入的控制加速度。
2.2 燃料最省开关控制策略
根据线性定常系统燃料最省控制原理[9],最省燃料控制问题为终端时刻固定的状态转移问题,且在状态转移过程中存在滑行段,控制流程见图3。

图3 燃料最省控制切换流程Fig.3 Switching sequence for minimum-fuel control
燃料最省控制的性能指标为:
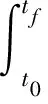
(12)
哈密尔顿函数为:
Hfuel(t)=|u(t)|+λT(t)[Ax(t)+Bu(t)]
(13)
根据最优控制原理,燃料最省控制的哈密尔顿函数沿最优轨线保持为常值。结合式(12)和式(13),极值条件可改写为:
λT(ti)B=-sgn[u(ti)],∀ti
(14)
当λTB<-1时,输入+|u|;当λTB>1时,输入-|u|;当-1≤λTB≤1时,航天器自由滑行。
根据式(3)以及图3可以得到非线性方程组式(15)和式(16)。
(15)
式(15)非满秩,虽然可以通过一些算法求解,但鲁棒性差,甚至得到错误解。因此,需要将协态变量状态转移方程和状态转移方程结合求解,得到控制切换时刻和协态变量初值,然后通过燃料最省的哈密尔顿函数特性和极值条件验证控制最优性。
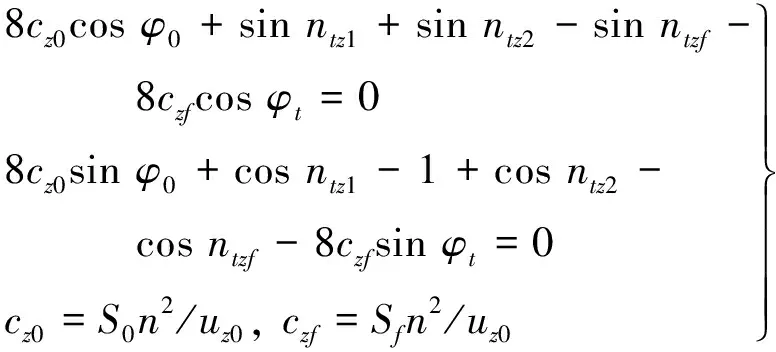
(16)
3 数值仿真及分析
3.1 仿真条件
卫星质量为100 kg,采用连续电推进方式进行编队构型控制,航天器的切向和法向安装电推力器,推力大小为8 mN。目标轨道根数为:a=6 887.135 km,e=0.0011,i=97.43°,Ω=283.67°,ω=90°。初始编队构型参数和目标构型参数如表1所示。由于电推进比冲很高,因此忽略控制过程中航天器的质量变化。
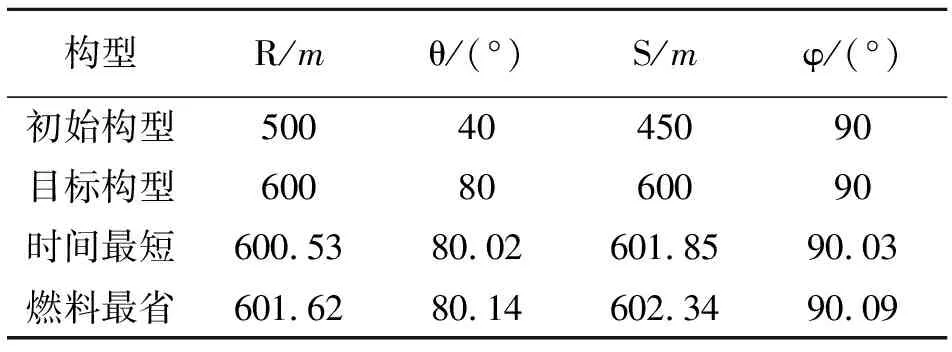
表1 初始构型和目标构型参数Table 1 Parameters of initial and target configuration
3.2 仿真结果及分析
燃料最省构型控制所耗费的时间大于时间最短编队构型控制,因此参考时间最短控制所耗费的时间,最终选取终端时间7 200 s作为燃料最省控制的时间历程。经计算,控制结束后的构型参数如表1所示。最优控制的切换时刻和消耗速度增量见表2和表3,最优控制验证曲线如图4~图7所示。

表2 平面内最优构型控制解Table 2 Solution of in-plane optimal control

表3 平面外最优构型控制解Table 3 Solution of out-plane optimal control
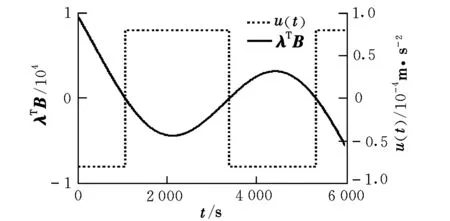
图4 时间最短面内控制验证曲线Fig.4 Validating graph of in-plane minimum-time control
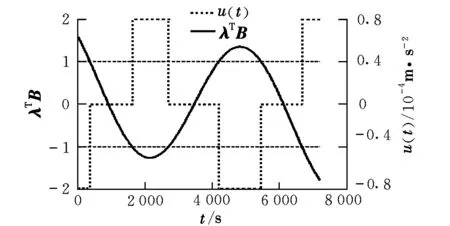
图5 燃料最省面内控制验证曲线Fig.5 Validating graph of in-plane minimum-fuel control
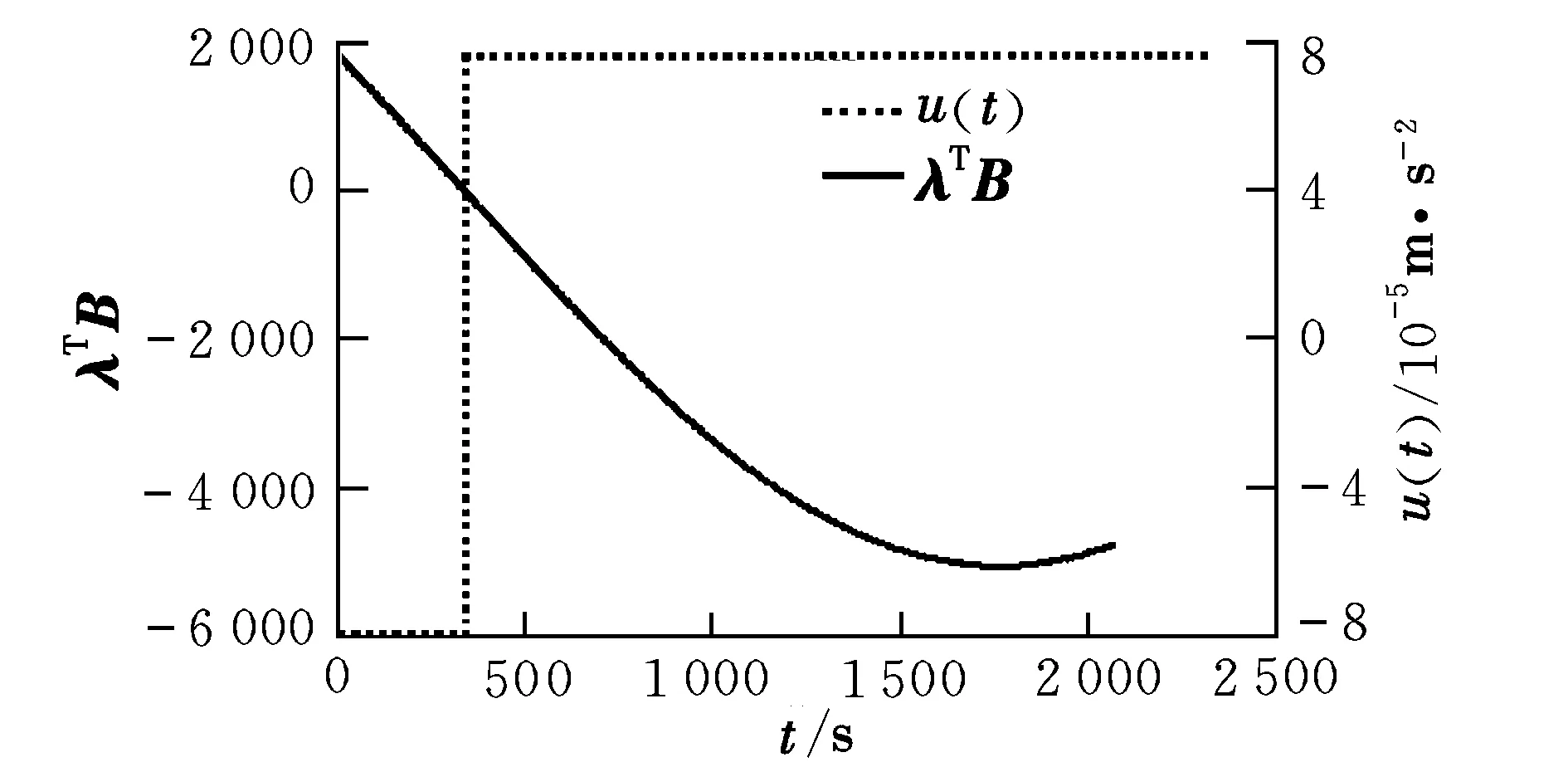
图6 时间最短面外控制验证曲线Fig.6 Validating graph of out-plane minimum-time control
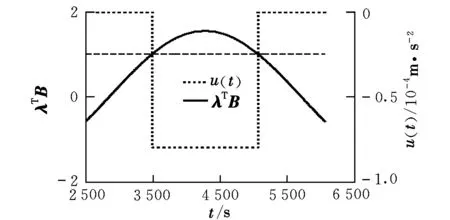
图7 燃料最省面外控制验证曲线Fig.7 Validating graph of out-plane minimum-fuel control
由表1的数据可以看出,时间最短和燃料最省控制结束后编队的构型均达到控制目的,误差较小。由图4~图7可以看出,切换控制律分别满足时间最短和燃料最省极值条件的约束,计算过程中哈密尔顿函数均满足最优性要求,证明所设计的线性定常系统燃料最省和时间最短控制律是正确、可行的。
4 结束语
本文设计了编队构型最优开关控制策略,仿真结果证明了该策略的正确性和可靠性。与其他求解连续推力编队控制问题相比,该方法充分利用编队飞行的动力学特性,不需要求解复杂的两点边界值问题,通过求解描述运动状态转移的非线性方程组即可以得到最优控制策略,大大减少了计算量。结合目前卫星推力器安装方式和电推进技术的研究现状,该方法非常适合编队构型控制的工程应用。
在本文研究过程中发现,求解最优控制策略对应的非线性方程组需要采用数值方法进行迭代求解,对初值选取仍较为敏感,且控制时序仍然需要根据迭代结果和最优控制的性质来进行人工判断。此外,燃料最省控制策略的响应速度往往太慢,达不到任务要求。因此,后续可针对高鲁棒性的控制策略求解方法以及控制时间、燃料的综合最优控制问题进行研究。
参考文献:
[1] 林来兴.分布式空间系统和航天器编队飞行辨析[J].航天器工程,2008,17(4):24-29.
[2] D’Amico S,Montenbruck O.Proximity operations of formation-flying spacecraft using an eccentricity/inclination vector separation [J].Journal of Guidance,Control,and Dynamics,2006,29(3):554-563.
[3] Carter T E,Alvarez S A.Quadratic-based computation of four-impulse optimal rendezvous near circular orbit [J].Journal of Guidance,Control,and Dynamics,2000,23 (1):109-117.
[4] 曹喜滨,董晓光,张锦绣,等.编队飞行自主控制的自适应方法[J].宇航学报,2012,33(7):903-909.
[5] Lee Sangjin,Park Sang-young.Approximate analytical solutions to optimal reconfiguration problems in perturbed satellite relative motion[J].Journal of Guidance,Control,and Dynamics,2011,34(4):1097-1112.
[6] Vadali S R,Schaub H,Alfriend K T.Initial conditions and fuel-optimal control for formation flying of satellites[R].AIAA-99-4265,1999.
[7] Carter T,Humi M.Fuel-optimal rendezvous for linearized equations of motion [J].Journal of Guidance,Control,and Dynamics,1992,15(6):1411-1416.
[8] Bryson A.Control of spacecraft and aircraft [M].Princeton:Princeton University Press,1994:103-113.
[9] Campbell M E.Planning algorithm for multiple satellite clusters[J].Journal of Guidance,Control,and Dynamics,2003,26(5):770-780.

