滚翼机滚转阶跃响应分析

杜帆, 胡峪

(西北工业大学 航空学院, 陕西 西安 710072)

0 引言

无人飞行器具有起降要求简单、隐身性能优异、机动性能突出等特点,近年来在军用及民用领域扮演着重要角色。滚翼机[1]作为一种全新类型的飞行器,近年来成为航空界的新兴研究热点。

目前对于滚翼机的研究尚处在初级阶段,总体参数对于滚翼机稳定性的影响尚未得到准确分析。本文提出滚翼机的动力学模型,通过仿真分析影响其滚转稳定性的因素,合理解释了验证机试飞过程中出现的三轴力矩耦合现象。

1 飞行器总体布局

滚翼机是一种由摆线桨提供升力的新型可垂直起降飞行器。在低雷诺数条件下,摆线桨具备高效率、高机动性的特点[1-3]。

滚翼机采用三轴式总体布局(见图1),机身前部安装有两个同向旋转的摆线桨,机身尾部安装有一个螺旋桨。两摆线桨产生升力的方向始终垂直于机身,升力大小由其转速决定。

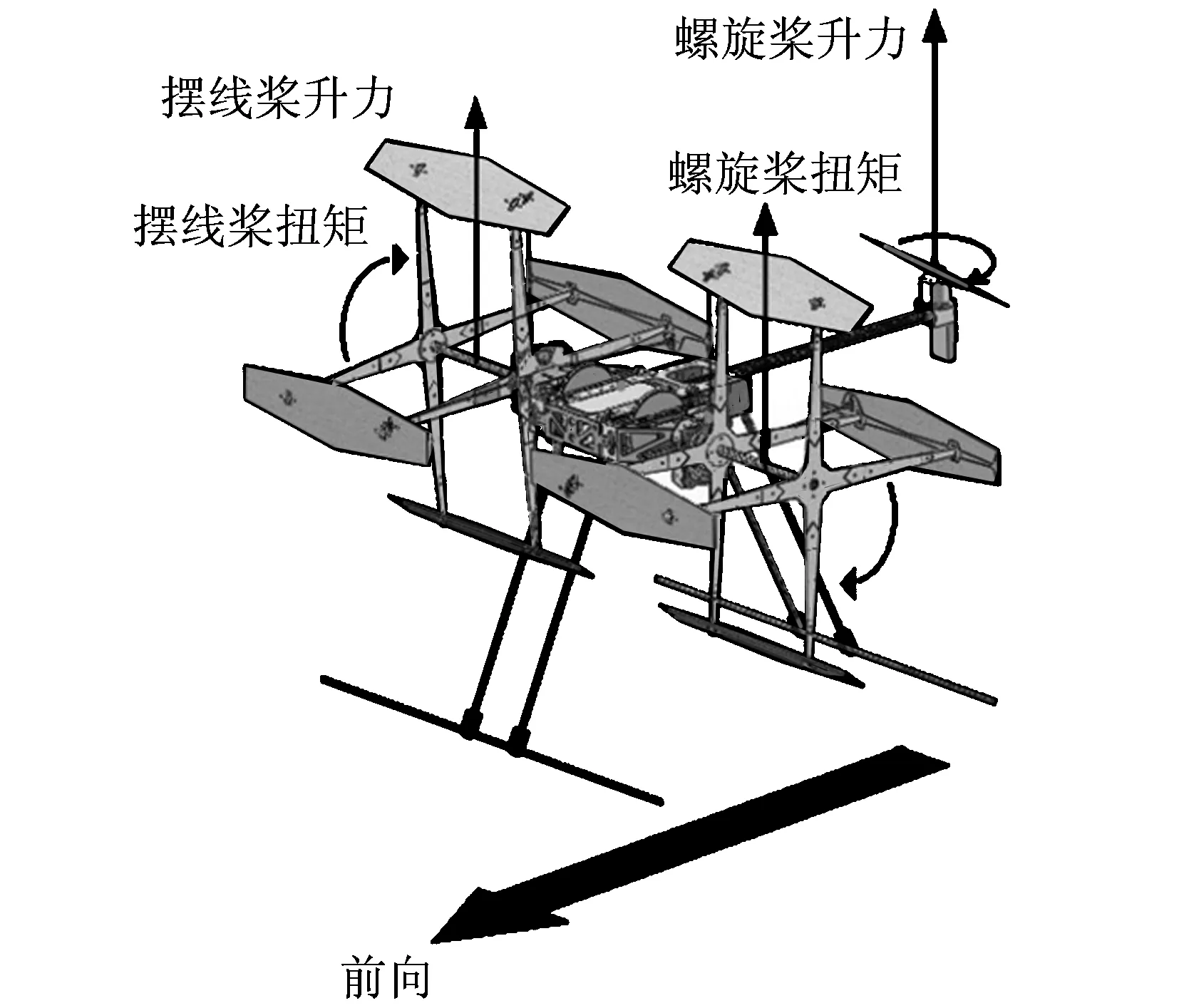
图1 滚翼机总体布局图Fig.1 Configuration of three-rotor cyclogyro

滚翼机受力分析如图2所示,两摆线桨的合力作为主要升力,控制滚翼机的上升和下降;两摆线桨的差动产生滚转力矩,控制滚翼机的滚转运动。尾部螺旋桨能够围绕尾杆进行左右偏转(见图3),垂直于机身的升力分量控制滚翼机的俯仰运动,平行于机身的升力分量控制滚翼机的偏航运动(见图4)。图中,F1,F2,T1,T2,ω1,ω2分别为左、右摆线桨的升力、扭矩、角速度;Ft,Tt,ωt分别为尾部螺旋桨的升力、扭矩、角速度;Gx,Gy,Gz分别为重力沿体轴系的分量;L1为摆线桨叶片中心到飞行器对称面的距离;L2为摆线桨旋转轴到飞行器重心cg的水平距离;L3为尾部螺旋桨旋转轴到飞行器重心的水平距离;L4为螺旋桨桨盘到尾杆旋转轴的距离;α为尾部螺旋桨的偏转角;h1为摆线桨旋转轴到飞行器重心的垂直距离;h2为尾杆旋转轴到飞行器重心的垂直距离。

图2 滚翼机受力分析图Fig.2 Forces and moments acting on cyclogyro

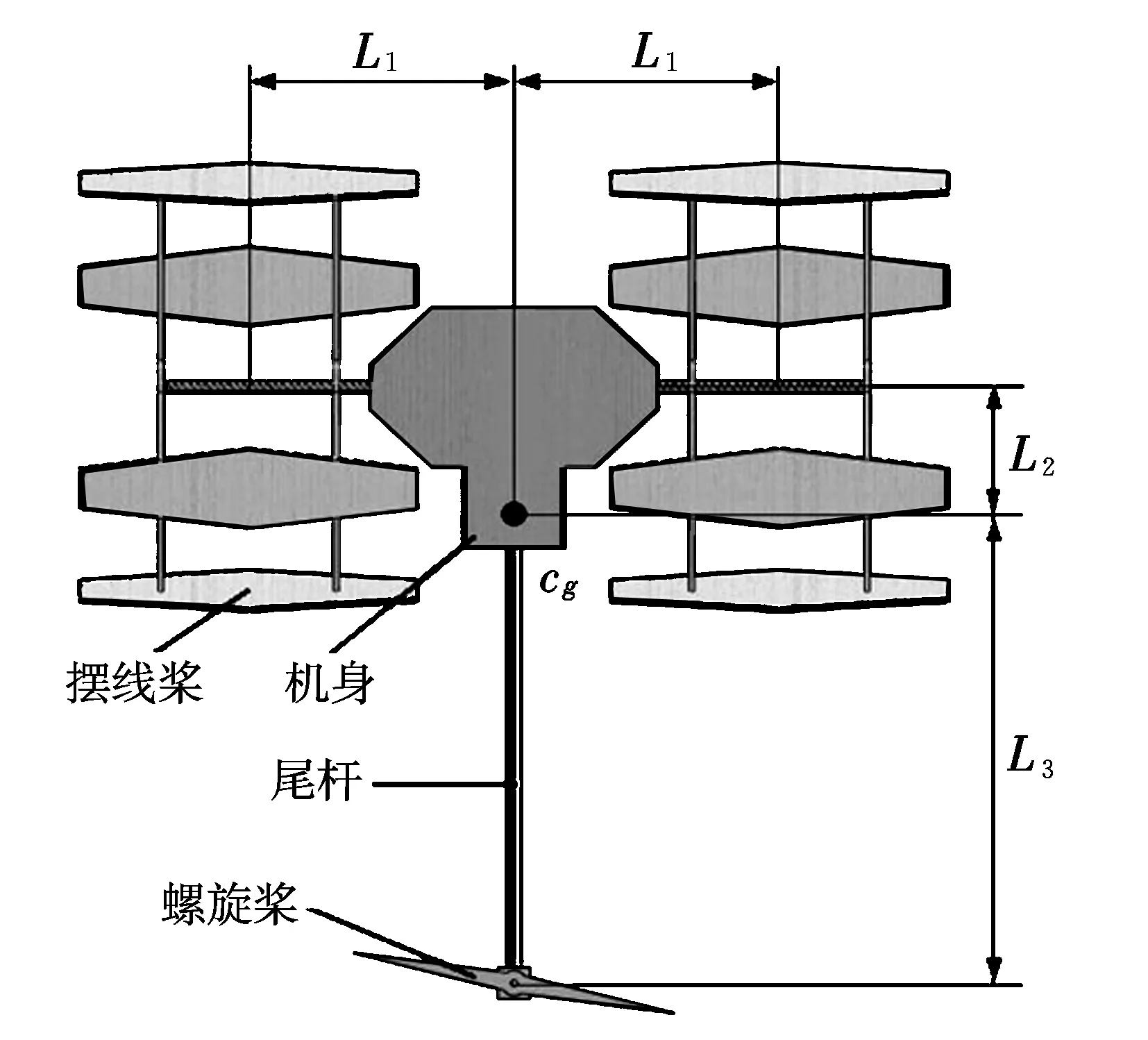
图3 滚翼机俯视图Fig.3 Bottom view of the dynamic model

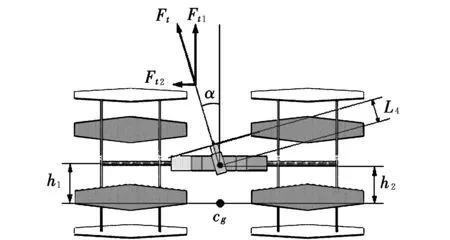
图4 滚翼机后视图Fig.4 Back view of the dynamic model

2 建立动力学模型

结合滚翼机受力分析,计算得到滚翼机在体轴系下所受到的合力及合力矩为:

∑Fx=-mgsinθ

∑Fy=mgcosθsinφ-Ftsinα

∑Fz=mgcosθcosφ-Ftcosα-F1-F2

∑Mx=F1L1-F2L1+Mgcr1+Mgcr2+Mgtr-

Ft2(h2+L4cosα)+Ft1L4sinα

∑My=F1L2+F2L2-Ft1L3+T1+T2+Mgtp

∑Mz=Ft2L3+Tt+Mgcy1+Mgcy2

式中,Mgcr为滚翼机在偏航时摆线桨产生的滚转力矩;Mgtr为滚翼机在俯仰时螺旋桨产生的滚转力矩;Mgtp为滚翼机在滚转时螺旋桨产生的俯仰力矩;Mgcy为滚翼机在滚转时摆线桨产生的偏航力矩。

综合以上方程式,在体轴系下建立滚翼机的动力学模型[4],具体表示如下:

式中,Rij为体轴系到地轴系的转换矩阵R的元素[5];Ix,Iy,Iz分别为滚翼机相对Ox轴、Oy轴、Oz轴的转动惯量。

3 仿真分析

根据所建立的动力学方程,对滚翼机进行动力学仿真,并对仿真结果进行分析。仿真过程为:滚翼机在第0～10 s处于初始稳定状态(滚转角、滚转角速度、俯仰角、俯仰角速度、偏航角、偏航角速度均为零),在第10 s输入-5°阶跃滚转角,滚翼机保持给定滚转角达到稳定状态(滚转、俯仰、偏航角速度均为零)。

3.1 飞行器悬停仿真分析

仿真结果显示,滚翼机在初始稳定阶段始终存在沿Ogyg轴的横向位移。受力分析如图5所示,尾桨在提供航向分力Ft2以抵消尾桨反扭矩Tt的同时,该分力Ft2使飞行器产生沿Ogyg轴向位移。因此滚翼机欲实现稳定定点悬停,机体必须保持一定的滚转角,这与普通直升机的悬停特点相似。

图5 滚翼机横向平移分析Fig.5 Analysis of cyclogyro translation

3.2 尾桨参数仿真分析

尾桨产生的升力作用于螺旋桨的桨盘中心,其相对于飞行器重心的距离由参数α,L4和h2决定。其中α是飞控系统控制参数,因此决定尾桨位置的几何参数主要为L4和h2。

仿真结果显示,参数L4的变化对于滚翼机的飞行稳定性能没有显著影响。该现象可由受力分析图(见图6)进行解释。

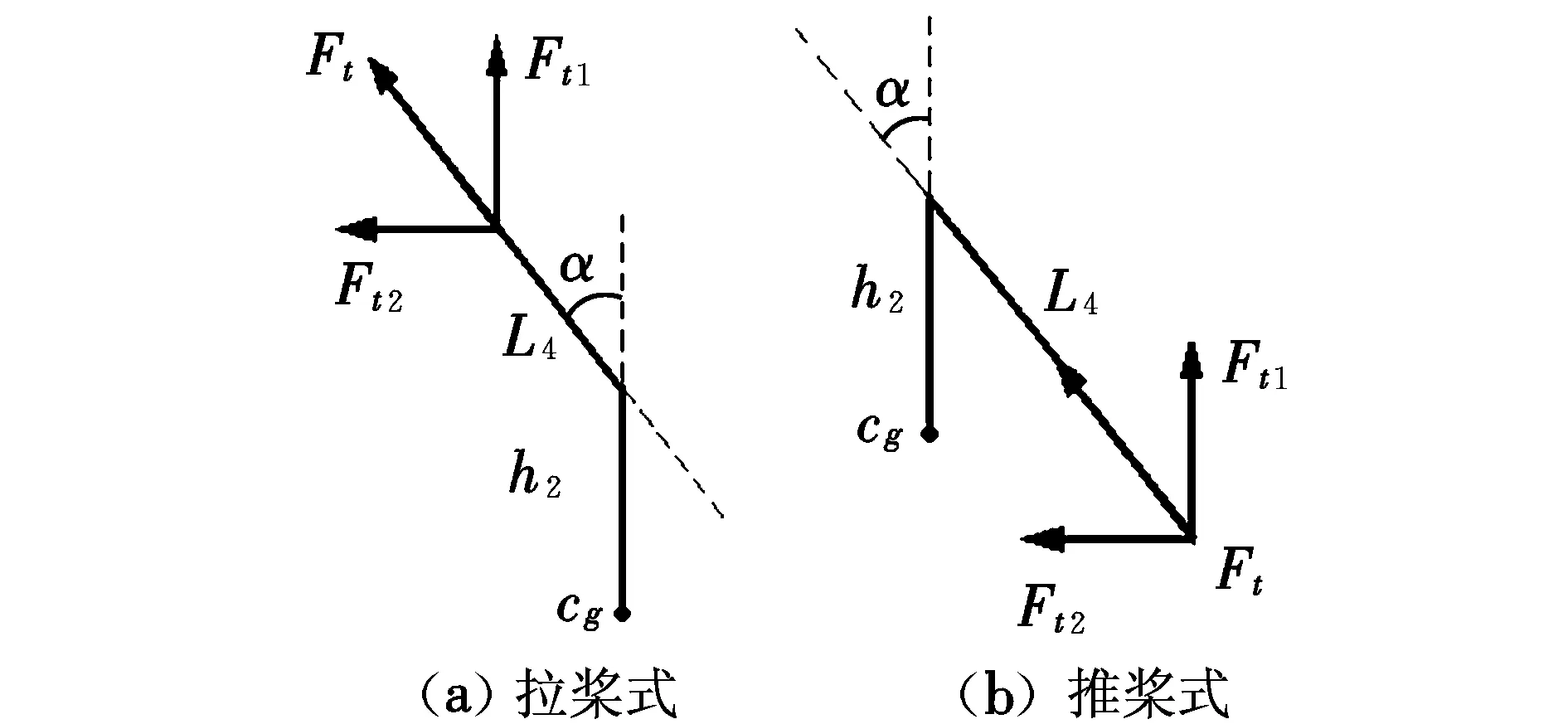
图6 尾桨受力分析简化图Fig.6 Forces of back view on cyclogyro

尾部螺旋桨在偏转过程中产生沿垂直方向和水平方向的两个分力Ft1,Ft2,同时两分力的作用力臂也随偏转发生改变。根据图6所示,尾桨的滚转合力矩∑Mt可表示为:

∑Mta=Ft2(L4cosα+h2)-Ft1L4sinα

=Ftsinαh2

=Ft2h2

∑Mtb=Ft1L4sinα+Ft2(h2-L4cosα)

=Ftsinαh2

=Ft2h2

由上述方程式可知，尾桨的滚转合力矩均为∑Mt=Ft2h2。因此,尾桨产生的滚转力矩仅与尾桨升力的水平分量Ft2及重心相对尾杆的距离h2相关。尾部螺旋桨桨盘相对尾杆的距离L4对于滚翼机的滚转没有影响,即等效于尾部螺旋桨产生的升力直接作用于尾杆上。

此外,还需对参数h2进行仿真分析。h2分别取值为:h2=+4 cm,h2=0 cm,h2=-4 cm(尾杆高于重心时为正值)。仿真结果如图7～图11所示。

图7 滚翼机滚转角速度曲线Fig.7 Roll angular velocity of cyclogyro

图8 滚翼机滚转角曲线Fig.8 Roll angle of cyclogyro

图9 滚翼机偏航角速度曲线Fig.9 Yaw angular velocity of cyclogyro

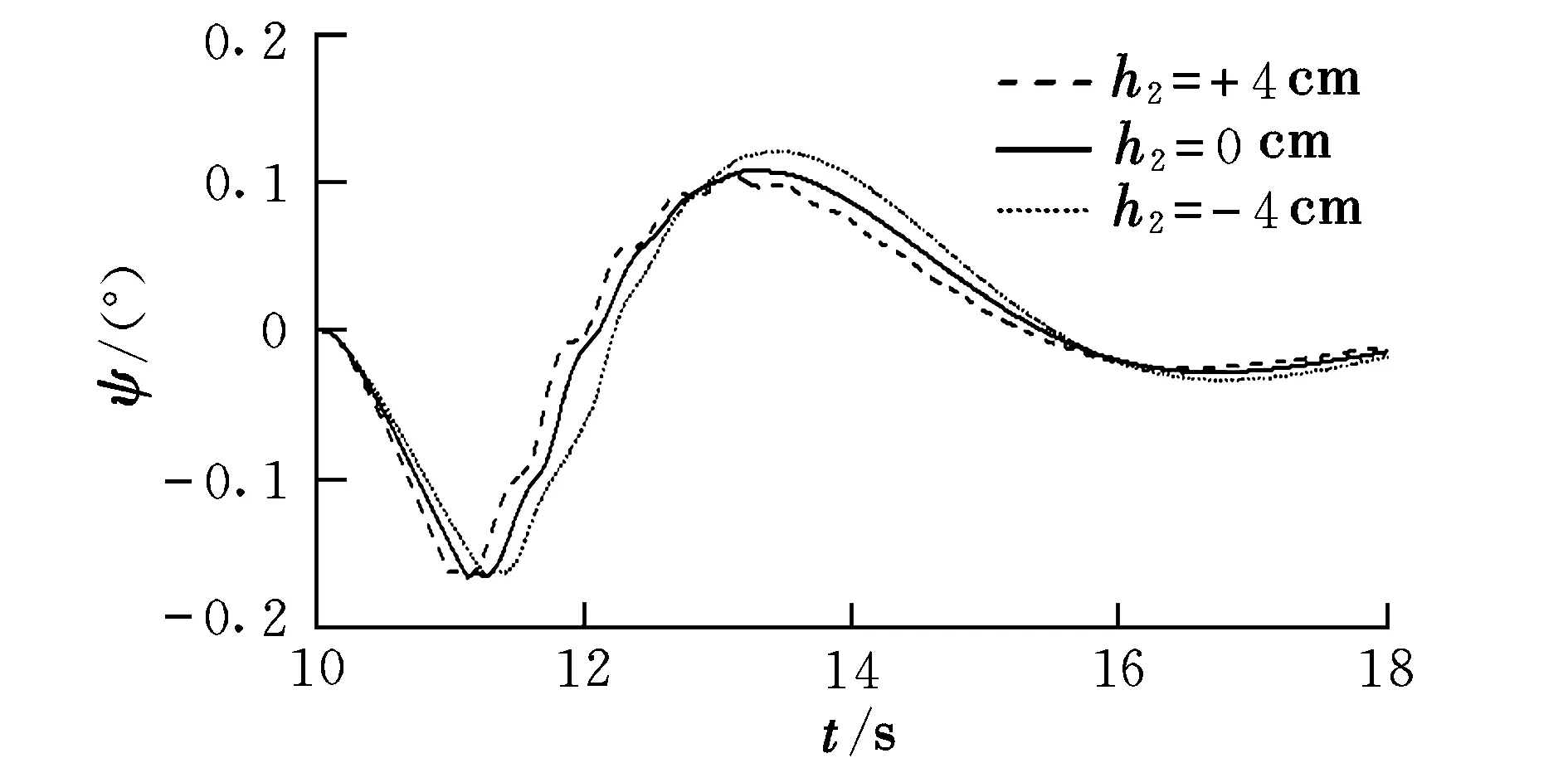
图10 滚翼机偏航角曲线Fig.10 Yaw angle of cyclogyro

图11 滚翼机俯仰角速度曲线Fig.11 Pitch angular velocity of cyclogyro

分析对比滚翼机滚转过程中滚转角、滚转角速度的变化曲线(见图7和图8),可得到如下结论:

(1)h2=+4 cm时,飞行器滚转角、滚转角速度的响应速度最快，但曲线振荡幅值大、频率高,滚转角超调量σ=58%,上升时间tr=0.85 s,峰值时间tp=1.60 s;(2)h2=0 cm时,飞行器滚转角、滚转角速度的响应速度居中,曲线振荡幅值及频率居中,σ=56%,tr=1.00 s,tp=1.72 s;(3)h2=-4 cm时,飞行器滚转角、滚转角速度的响应速度最慢，但曲线振荡幅值小、频率低,σ=75%,tr=1.14 s,tp=2.06 s。

对比3组数据可以发现,当h2>0时，系统的超调量较小，上升时间及峰值时间较短。

参数h2对滚翼机产生影响的原因为:摆线桨的转动惯量为螺旋桨的45倍,其产生的陀螺力矩对于滚翼机具有显著影响。影响过程为:当飞行器左滚时,摆线桨产生的陀螺力矩使滚翼机左偏航,因此滚翼机具有滚转偏航耦合现象(见图9、图10);飞控系统将控制尾桨左偏以抵消该陀螺力矩,同时尾桨的水平分力会产生滚转力矩Ft2h2,该滚转力矩作用于滚转控制过程中,将对滚转控制产生影响。当h2>0时,该滚转力矩方向与机体滚转角速度方向相同,从而加速飞行器的滚转。当h2=0时,该力矩大小为零,不会对机体滚转产生影响。当h2<0时,该滚转力矩方向与机体滚转角速度方向相反,从而阻碍飞行器的滚转。

滚翼机滚转过程中俯仰角速度变化曲线如图11所示。引起俯仰角速度变化的原因为:在滚转过程中,滚翼机的高度将会产生变化;为了维持飞行高度,摆线桨及螺旋桨的升力将产生变化,最终引起俯仰角速度的变化。因此滚翼机具有高度俯仰耦合现象。

由此可知,三轴式布局滚翼机是一种存在复杂耦合关系的新型飞行器,保持其稳定性的难度高于其他类型无人机。仿真结果合理解释了滚翼机在试飞过程中(见图12)出现的三轴力矩强耦合现象。

图12 滚翼机试飞场景Fig.12 Flight test scene of cyclogyro

4 结束语

本文针对三轴式布局滚翼机,建立了完整的动力学模型,首次通过仿真分析揭示了总体参数对滚翼机滚转稳定性的影响。仿真结果能够合理解释飞行试验中出现的三轴力矩耦合现象,并指出了改善其滚转稳定性的参数设计方法。本文对今后此类滚翼机的设计研究具有一定的指导作用及技术价值。目前,尚未完全完成滚翼机三轴稳定性的研究,因而下一步亟需对偏航和俯仰稳定性进行探索,从而更好地改善三轴式滚翼机的飞行稳定性。

参考文献：

[1] Curtis Boirum,Scott Post.Review of historic and modern cyclogyro design[R].AIAA-2009-5023,2009.

[2] Yu Hu,Kah Lim,Wen Hu.The research on the performance of cyclogyro[R].AIAA-2006-7704,2006.

[3] Moble Benedict,Mattia Mattaboni,Inderjit Chopra,et al.Aeroelastic analysis of a MAV-scale cycloidal rotor [R].AIAA-2010-2888,2010.

[4] 高浩,朱培申,高正红.高等飞行动力学[M].北京:国防工业出版社,2004:1-6.

[5] 聂博文.微小型四旋翼无人直升机建模与控制方法研究[D].长沙:国防科学技术大学,2006.