甲板运动对舰载机弹射起飞特性的影响
蔡丽青, 江驹, 王新华, 潘婷婷
(南京航空航天大学 自动化学院, 江苏 南京 210016)
0 引言
舰载机弹射起飞是一个多系统的复杂动力学过程[1],此过程受到多种因素的影响。其中,甲板运动对弹射起飞的影响尤为明显,主要表现为舰载机离舰后下沉量和飞行姿态的变化。文献[2]通过对5种不同飞机的弹射起飞进行测试,制定了相应的安全准则。国内在这方面的研究主要是通过建模仿真的方式:如贾忠湖等[3]建立了舰载机弹射起飞数学模型,分析了舰面纵摇对弹射起飞的影响;张磊等[4]对有浪条件下舰载机弹射起飞建模进行了研究,分析了中等海况下航母的摇摆对舰载机弹射起飞的影响;郭元江等[1]对复杂环境下舰载机弹射起飞进行了建模分析,研究了甲板运动、甲板风与舰艏气流、地面效应等因素对弹射起飞的影响。上述文献均对甲板纵摇运动对飞机离舰后下沉量的影响进行了较深入的研究。文献[4]还着重研究了甲板横摇引起起落架载荷的变化,但未对舰载机飞行姿态与侧向位移的变化进行分析。
本文首先对甲板运动影响下的舰载机弹射起飞过程运动与受力情况进行分析,建立舰载机弹射起飞全过程数学仿真模型。在此基础上,着重从甲板沉浮、俯仰、横滚运动对舰载机弹射起飞的影响进行了较全面的分析,并针对弹射起飞策略设计提出了建议。
1 舰载机弹射起飞全过程建模
舰载机弹射起飞全过程模型由舰载机非线性气动力学模型、弹射器模型、起落架模型和电传飞行控制系统[5]组成,其结构如图1所示。
本文以F/A-18飞机模型为研究对象,对弹射起飞运动情况进行动力学和运动学分析。其中弹射器和起落架模型通过提供附加力和力矩的方法加入到飞机模型中,而飞机的飞行姿态、高度、位移则反馈给弹射器和起落架模型形成闭合回路。甲板运动通过作用于起落架模型达到影响飞机飞行特性的目的。舰载机离舰后1~2 s飞行员才对飞机进行操纵,在此之前,舰载机弹射起飞过程中飞机电传飞行控制系统中驾驶杆输入为零。

图1 舰载机弹射起飞模型结构图Fig.1 Structure of carrier-based aircraft catapult launch model
1.1 舰载机弹射起飞数学建模
在机体坐标系上,增加弹射器模型与起落架模型的分力,舰载机弹射起飞力和力矩方程组都会发生变化,飞机运动学及动力学六自由度微分方程组[6]可采用如下形式描述:
(1)力方程组:

(1)
式中,Fx′,Fy′,Fz′为在机体坐标系下,弹射器与起落架对舰载机的作用力在机体坐标轴上的投影。
(2)力矩方程组:
(2)
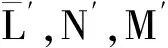
其余方程组不变,具体可参见文献[6]。
1.1.1 弹射器模型的建立
弹射器采用C13-1型蒸汽弹射器,根据文献[7]给出的参数,得到如图2所示的弹射力Ft随弹射位移Lt的变化曲线,其中弹射冲程为302 ft(约92 m)。

图2 弹射力随弹射位移变化曲线Fig.2 Catapult force vs stroke curve
1.1.2 起落架受力及模型建立
对起落架模型进行简化处理如图3所示。图中上部质量即为弹性支承质量,包括机身、机翼、尾翼、缓冲器外筒等质量,以及空气弹簧支撑的质量M;下部质量为非弹性支承质量,包括缓冲器活塞杆、刹车装置、轮胎等质量,对于小车式起落架还要包括车架及非空气弹簧支撑的质量m。ZM为上部质量在竖直方向上的位移,Zm为下部质量在竖直方向上的位移。在弹射起飞过程中,飞机受到的地面支持力随起落架压缩量与轮胎形变量的变化而变化。

图3 起落架简化示意图Fig.3 Simplified schematic diagram of the landing gear
假设舰载机弹射起飞时上部质量与下部质量的加速度一致,忽略轮胎在变形过程中引起的加速度不一致。忽略舰载机发动机安装角。
对起落架进行受力分析,得到起落架的运动方程。起落架上部质量的运动方程:
Mg-Fscosθ+Nssinθ-L(cosθcosα+
sinθsinα)+D(sinθcosα-
cosθsinα)-Tsinθ=Mazg
(3)
起落架下部质量在x轴和z轴的运动方程:
Fssinθ+Nscosθ-f=maxg
(4)
mg+Fscosθ-Fz-Nssinθ=mazg
(5)
缓冲器的行程和速度:
(6)
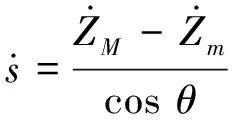
(7)
式中,Fs,Ns分别为起落架缓冲支柱法向力和轴向力;L,D,T分别为飞机的升力、空气阻力和发动机推力;θ和α为飞机俯仰角和迎角;f为轮胎摩擦力;Fz为轮胎支持力;s为起落架缓冲器行程;s0为缓冲器初始行程。由于篇幅有限,具体计算公式参见文献[8]。
1.2 甲板运动模型的建立
航母在海上受到风、浪等因素的影响,产生六自由度的运动,一般包括沿航母三坐标轴的直线运动(纵荡、横荡、沉浮)和围绕三坐标轴的旋转运动(横滚、俯仰、偏航)。本文着重考虑甲板沉浮运动、俯仰运动和横滚运动对弹射起飞的影响。根据相关文献,给出航母在30 kn(15.44 m/s)典型速度行驶时,中等海况下的甲板运动模型[9]为:
沉浮运动:
Zs=1.22 sin(0.6t)+0.3 sin(0.2t)
俯仰运动:
θs=0.5 sin(0.6t)+0.3 sin(0.63t)+0.25
横滚运动:
φs=2.5 sin(0.5t)+3.0 sin(0.52t)+0.5ωh
由上式仿真可知,中等海况引起的甲板运动幅值为:沉浮1.52 m,俯仰1.05°,横滚6°。甲板运动通过与起落架的相互作用对舰载机产生附加的力和力矩,从而对舰载机弹射起飞产生影响。
2 甲板运动对弹射起飞过程影响分析
本文算例舰载机采用F/A-18模型,航母航速为30 kn,中等海况,不考虑气流对舰载机弹射起飞的影响。
2.1 甲板沉浮运动影响分析
只考虑航母做沉浮运动,采用1.2节所述甲板沉浮运动模型,从舰载机起飞时刻开始计甲板运动。舰载机升降舵预置偏角取-3°,在离舰时刻取甲板运动相位值ωh分别为0°,90°,180°和270°,得到舰载机弹射起飞仿真结果如图4和表1所示。
根据图4的仿真结果可知,飞机在弹射阶段运动轨迹与甲板运动位移轨迹相符,在t=2.85 s左右飞机脱离弹射器。

图4 飞机飞行高度变化曲线Fig.4 Flight altitude curves

ωh/(°)h/mαmax/(°) 00.484.56901.304.651802.104.86 2701.434.71
根据表1可知,在舰载机离舰时刻,当ωh=0°时,即甲板沉浮为零,沉浮速度正向最大;当ωh=90°时,即沉浮位移正向最大,沉浮速度为零;当ωh=180°时,即沉浮位移为零,沉浮速度负向最大;当ωh=270°时,即沉浮位移负向最大,沉浮速度为零时,飞机下沉量达到1.43 m。但以上各种情况中飞机的迎角变化不是很大。
对比可知,相位为180°时最不利于舰载机起飞,相位0°时最有利于舰载机起飞。甲板沉浮速度为其主要影响因素。
2.2 甲板俯仰运动影响分析
只考虑航母做俯仰运动,采用1.2节所述甲板俯仰运动模型,仿真条件与2.1节相同,得到舰载机弹射起飞仿真结果如图5和表2所示。
由图5可知,舰载机在弹射阶段运动轨迹与甲板运动位移轨迹相符。航母作俯仰运动,相当于舰载机在一个变坡度的跑道上起飞,相较于无俯仰运动,飞机受力情况发生了变化,导致飞机离舰速度与离舰后飞行姿态发生变化。

图5 飞机飞行高度变化曲线Fig.5 Flight altitude curves
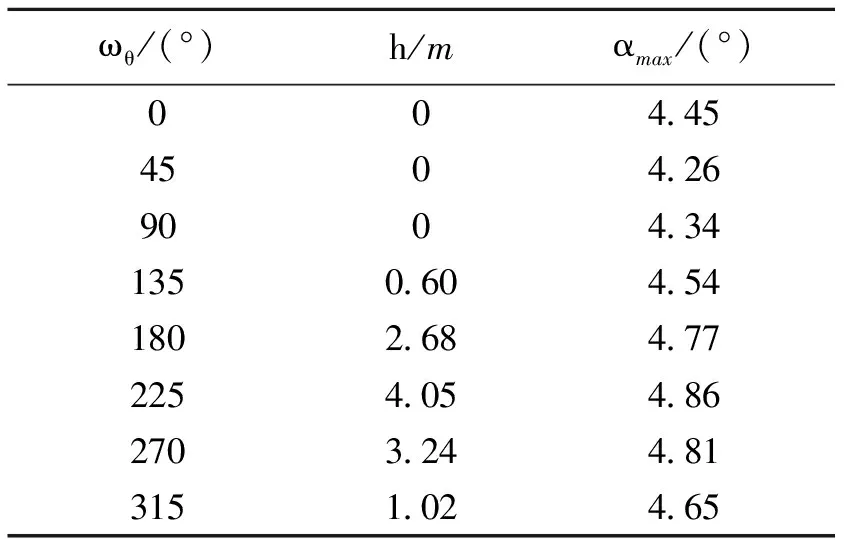
ωθ/(°)h/mαmax/(°) 004.45 4504.26 9004.34 1350.604.54 1802.684.77 2254.054.86 2703.244.81 3151.024.65
由表2可知,根据舰载机离舰安全准则[2],舰载机弹射起飞的甲板俯仰角相位ωθ安全范围为-45°~135°。在ωθ为0°~90°时,甲板俯仰角为正值,俯仰角速率由正向最大值逐渐减小为零。在此状态下,飞机下沉量为零。在ωθ为90°~135°时,甲板俯仰角为正值,俯仰角速率由零减小为负值。此时,飞机下沉量开始增大,但未超过安全范围。在ωθ大于135°时,飞机下沉量随相位增大而增大,直至超过安全范围。在ωθ为180°~270°时,甲板俯仰角为负值,俯仰角速率由负向最大增大为零后继续增大。此时,飞机下沉量均超过安全准则规定的范围(3.048 m)。在ωθ大于270°时,飞机下沉量随相位增大而减小。飞机迎角变化趋势与甲板俯仰对飞机起飞的影响程度成反比,越有利于飞机起飞的甲板运动状态对应的离舰最大迎角越小,但都在安全范围内。
根据以上分析可知,甲板俯仰角为正值给飞机起飞带来正面影响,反之则为负面影响;甲板俯仰角速率为正值也会对飞机起飞带来正面影响,但不如俯仰角的影响明显。因此严格地说,若要保证舰载机安全起飞,最好的相位范围为0°~90°,即甲板俯仰角为正值,俯仰角速率亦为正值的时刻。
2.3 甲板横滚运动影响分析
考虑航母的实际情况,本文假设弹射跑道在航母对称中心线右侧,弹射跑道与航母对称中心线夹角为5.223°,弹射滑跑时弹射器对飞机侧滑有一定限制,航母做横滚运动,向右滚转为正。采用1.2节所述甲板横滚运动模型,仿真条件与2.1节相同,得到舰载机弹射起飞仿真结果如图6~图8和表3所示。

图6 飞机侧向偏移曲线Fig.6 Lateral deviation curves

图7 飞机飞行高度变化曲线Fig.7 Flight altitude curves

图8 飞机滚转角曲线Fig.8 Roll angle curve
由仿真结果可知,航母做横滚运动会导致飞机滚转角发生改变,离舰后轨迹产生侧向偏移,下沉量发生变化。这是由于飞机滚转角使飞机升力在垂直方向的分量减小,从而导致飞机离舰后高度下降。同时考虑到弹射起飞跑道不在航母对称面上,当甲板做横滚运动时会给飞机附加一个垂向速度和初始滚转角,导致飞机离舰时刻速度方向与姿态角发生变化。并且由于弹射跑道与航母中心线也有一定夹角,导致航母滚转时飞机俯仰角也会产生一定变化。因此,得到的飞机离舰后下沉量曲线不如前两小节具有明显的规律。
以甲板横滚运动相位ωφ=0°为例,甲板横滚角为零,横滚角速率正向最大,即甲板具有向右滚转的趋势,飞机发生逆偏航,先向左偏移再向右偏移。飞机离舰时具有一个竖直向下的附加速度,离舰后飞机滚转角先增大后减小,因此飞机下沉较快,爬升也较快。ωφ=90°时,甲板横滚角正向最大,横滚角速率为零,即甲板向右滚转,飞机离舰后先向右偏移后向左偏移。飞机离舰时竖直方向附加速度几乎为零,滚转角先减小为零后增大,因此飞机下沉较慢,爬升也较慢。
相比之下,ωφ=180°时,飞机滚转角变化幅度与相位为0°时相仿,横滚角速率负向最大,导致飞机下沉速率小于相位为0°时的下沉速率,下沉量也较小。ωφ=270°时,飞机滚转角变化幅度与ωφ=90°时相仿,但由于弹射跑道与航母对称中心线有固定夹角,导致ωφ=270°时飞机相对于水平面的俯仰角小于零,不利于飞机起飞,因此飞机下沉量较大。

表3 不同横滚相位下仿真结果对比Table 3 Comparison of simulation results for different phase of rolling motion
综上所述,甲板横滚运动对舰载机起飞的影响比较复杂。在离舰初始时刻甲板对飞机附加速度影响飞机的下沉速率。离舰后几秒内,飞机滚转角的变化对飞机爬升速度产生一定影响。同时,甲板横滚带给飞机的俯仰角变化也在一定程度上影响飞机的起飞特性。因此,需要飞行员根据甲板的运动情况预置适当升降舵偏角以及在离舰后尽快对飞机进行操纵,才能保证舰载机起飞的安全性。
3 结论
本文建立了舰载机弹射起飞全过程数学模型,对中等海况下的甲板沉浮、俯仰和横摇对舰载机弹射起飞的飞行特性影响进行了研究,得到以下结论:
(1)甲板沉浮运动会对舰载机弹射起飞离舰后下沉量产生一定影响。其中甲板沉浮速度为甲板沉浮的主要影响因素。
(2)甲板俯仰运动对舰载机弹射起飞的影响大于甲板沉浮与甲板横摇运动。主要影响因素为甲板俯仰角。相位范围在-45°~135°之间可满足舰载机安全起飞的要求。可通过预置适当的升降舵偏角和离舰后飞行员对飞机进行操纵,来减小甲板俯仰运动的影响。
(3)由于弹射起飞跑道不在航母对称面上,甲板横摇对舰载机弹射起飞影响比较复杂,甲板横摇不仅会对舰载机离舰后的下沉量产生影响,还会改变舰载机离舰后的飞行姿态,使其在离舰后产生侧向偏移。因此,飞行员需要在离舰后及时对飞机进行控制,以抑制甲板横摇对舰载机离舰带来的不利影响。
参考文献:
[1] 郭元江,李会杰,申功璋,等.复杂环境下舰载机弹射起飞环境因素建模分析[J].北京航空航天大学学报,2011,37(7):877-881.
[2] Lucas C B.Catapult criteria for a carrier based airplane[R].United States:AD702814,1968.
[3] 贾忠湖,高永,韩维.航母纵摇对舰载机弹射起飞的限制研究[J].飞行力学,2002,20(2):19-21,26.
[4] 张磊,王海峰,宋笔锋.有浪条件下舰载机弹射起飞建模研究[J].科学技术与工程,2012,12(3):601-606.
[5] 宋翔贵,张新国.电传飞行控制系统[M].北京:国防工业出版社,2003:44-65.
[6] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2006:56-59.
[7] Naval Air Engineering Center.MIL-STD-2066(AS) Military standard catapulting and arresting gear forcing functions for aircraft structural design[S].United States:Department of the Navy Air Systems Command,1981.
[8] 聂宏.飞机起落架的缓冲性能分析与设计及其寿命计算方法[D].南京:南京航空航天大学,1990.
[9] 杨一栋.舰载飞机着舰引导与控制[M].北京:国防工业出版社,2007:30.

