贝叶斯计算理论在亲子鉴定中的应用

杨 达 崔 文

(济宁医学院法医学与医学检验学院，山东 济宁 272067)

1 前言

法医物证学主要解决亲权鉴定及个体识别问题。解决这2大问题首先要利用分子生物学的理论知识和实验技术对人体的生物性检材进行处理，对遗传标记进行分型，进而利用数学计算理论对分型结果进行量化，从而判断个体之间是否存在亲缘关系。

最初，主要是采用血型，血清型，酶型等遗传标记的分技术来解决法医物证学中亲权鉴定、个体识别等问题，因此法医物证学又称法医血清学。当前DNA遗传标记已经基本取代了传统的遗传标记，成为法医物证鉴定的主流。第1代用于法医物证鉴定的遗传标记是VNTR(可变数目串联重复序列)，存在于小卫星序列当中。其核心技术是分子杂交。适用于法医物证鉴定的第2代遗传标记是STR(短串联重复序列)，由于STR等位基因片段具有扩增效率高，多态性好，等位基因数目有限、分型较易等优点，因此，被世界上大部分法医物证实验室采用进行亲子鉴定。具体方法是首先使用ABI公司的3500测序仪对生物性检材进行处理，得出STR遗传标记分型结果，然后计算出相应的亲权指数，得出鉴定结论。可用于法医物证的第3代遗传标记是SNP(单核苷酸多态性)。目前由于实验技术的局限以及成本等问题，还未被实验室广泛采用。

当通过相应的实验技术对生物检材进行处理得出相应的遗传标记分型结果之后，就需要根据相应的算法计算出亲权指数等相应法医学参数，进而对分型的结果进行解释。

2 方法

2.1 标准三联体亲权指数

常规亲子鉴定多见于父子关系鉴定，即母子关系肯定，要求鉴定假设父与孩子是否有亲生关系，习惯上称为标准三联体鉴定。

最早关于亲权计算的理论是Essen-Möller于1938年提出的[1]，Essen-Möller和他的同事Quensel设计了一个公式可用于进行标准三联体即假设父-子-母亲权鉴定，该公式的出现第一次使血清的表型能够用数学计算的方式进行解释和表达，进而作为亲权鉴定的依据。该公式设置了两个变量X和Y, X代表“亲子关系存在”，Y代表“不存在亲子关系”，该公式主要从父亲的基因型角度考虑，具体计算时，X可以理解为当假设父为孩子亲生父亲时，假设父出现基因型的概率，Y代表假设父非孩子生父，为人群中随机个体时出现该基因型的概率。

假设嫌疑父亲的基因型为AB,生母的基因型为C,孩子的基因型为BC。X主要通过计算该假设父-子-母基因型出现频率与该子-母基因型组合出现频率的比值来反应假设父基因型出现的概率。假设群体中A、B、C等位基因频率分别为a、b、c, E为除A、B、C外群体中所有其它等位基因的总和，因此E的频率e=1-a-b;

此时X可以表示为：

Y代表在该群体中该嫌疑父亲基因型出现的概率，可以表示为:

此时亲权关系存在的可能性为：

该公式和我们今天所采用的父权相对机会RCP完全一致，只是考虑的角度不同，然而 Essen-Möller的研究在多年的时间里都没有被很好地认识。直到Essen-Möller的公式被发表20多年后，Ihm发现了Essen-Möller的公式可以直接通过贝叶斯理论进行推导，即将贝叶斯公式父母中体现先验概率的部分化为肯定和否定亲权两部分[2]，然后计算所有个体基因表型概率，当肯定与否定两部分的前概率相等时，可得到和Essen-Möller公式相同的结论。在1956年，Güürtler建议使用比率，即PI=X/Y作为亲子鉴定过程中的一个基本指标，去揭示亲权关系可能性[3]，此后，Ihm建议对贝叶斯计算理论中的前概率进行调整[4]，从而可以将除遗传标记分型结论之外与案件相关的证据考虑到计算过程中，这种方法引入两个参数π0和π1，分别代表为在未考虑遗传标记分型结果时肯定和否定亲权关系的概率， 即PI=(π0X)/(π1Y)，当PI大于一个数值的时候，通常是100或者1000，可以得出肯定亲权关系的结论。

目前，标准三联体即母-子-嫌疑父鉴定可以通过构建假说，然后采用贝叶斯计算理论根据构建好的假设对DNA分型结果进行计算[5]，获得亲权指数的方式进行，此时亲权鉴定可以抽象成两个对立的假说:

H0:被鉴定的男子就是孩子的生父(即X部分)

H1:人群中的随机男子是孩子的生父(即Y部分)

假设E代表孩子基因型，假设父、生母、随机父亲、孩子分别用AF、M、RF、C来表示，Cf代表孩子的父系等位基因，Cm代表孩子的母系等位基因，父权指数PI可以表示为：

其中PAF(Cf)代表假设父AF提供等位孩子父系基因Cf的概率，在计算PI的时候需要注意随机父亲所在的人群要符合Hardy-Weinberg 平衡定律。在具体进行亲子鉴定的过程中，还需要应用乘法规则进行CPI(累计父权指数)计算，即将各个独立的遗传标记PI值想乘，得出一个累计的父权概率的值即CPI值。在进行CPI计算的时候，应该注意各个基因座是否相互独立，即不存在连锁不平衡。

Li 和Chakravarti曾经宣称Essen-Möller的理论是无效的，亲权指数PI也不是一个比率[6]，然而，他的观点很快受到了驳斥[7-9]。Elston认为Essen-Möller方法充分利用了鉴定过程中所有基因分型相关信息，并从最小方差角度证明了该方法是最有效的[7]。Baur证明了PI是一个衡量亲权关系的合适比率，这是由于PI是基于两个相互排斥的假说(H0和H1)基础上根据被检测个体的不同表型集合计算出来的两个不同概率的比值[8]。Mickey 通过实际案例的分析证明了PI是一个有效的衡量亲权关系的指标[9]。

2.2 双亲皆疑亲权指数计算

当母子和父子关系都不确定，需要鉴定某一对夫妇 ( 或男女)是否为孩子的亲生父母 ，称之为双亲皆疑亲子鉴定。三联体形式可表示为：假设父-子-假设母。这种情况在落户鉴定中比较常见，即孩子与父母双方关系均无法确定。

双亲皆疑亲子鉴定的假说不同标准三联体，可表示为：

H0：假设父(AF)、假设母(AM)是孩子的亲生父母。

H1：随机男子(RF)、随机女子(RM)是孩子的亲生父母。

陆惠玲等认为上面的方法在计算Y时只考虑孩子是随机男子和随机女子所生这一种情况，不够全面[10]。实际上，如果孩子不是假设父、假设母这两人所生，共包含有三种可能性：1)孩子是随机男子与随机女子所生；2)孩子是假设父(AF)与随机女子(RM)所生；3)孩子是假设母(AM)与随机男子(RF)所生。因此又增加了两个假说：

H2：假设父(AF)、随机女子(RM)是孩子的亲生父母。

H3：随机男子(RF)、假设母(AM)是孩子的亲生父母。

此时PI计算公式可以修改为：

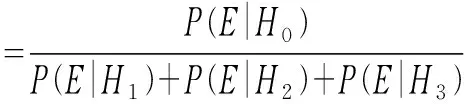
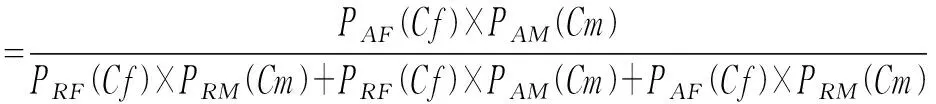
此种方法有也具有一定的参考价值。

2.3 考虑突变的亲权指数

如前所述，大多数实验室是通过短串联重复序列位点(STR)的分析开展亲子鉴定工作。用于法医学目的的DNA短串联重复序列STR)容易发生突变， STR位点的总体突变率为5×10-4到 7×10-3[11-12]。即使父子存在肯定的亲权关系，由于突变现象的存在也能使嫌疑父遗传了一个看起来不可能遗传的基因给孩子，真正的生父有可能因此被排除，这是一种不符合遗传规律的情况--孩子的基因型和父母的基因型并不符合孟德尔遗传规律。这种情况必须对之前的PI计算公式进行修改，从而将突变发生率考虑进去。性别和DNA片段的长度是影响突变发生的两个重要因素[11]。此外由于我们在计算过程中假定基因频率是稳定的，因此，考虑突变率的静态性，即该突变率计算方式可以使人群基因频率在世代遗传过程中保持相对稳定，也是非常重要的。

突变情况下，关于PI计算的两个相对独立的假说可以表示为：

H0:被鉴定的男子就是孩子的生父，不符合遗传规律的情况是由突变引起的

H1:人群中的随机男子是孩子的生父

假设Cf代表孩子的父系等位基因，Cm代表孩子的母系等位基因,Fc代表假设父遗传给孩子的等位基因，即发生突变的等位基因，μI→J代表等位基因I 突变为J的特异突变率，I→J代表了鉴定过程中可能发生突变的基因由I突变为J。由于Fc≠Cf，因此PI修改为：

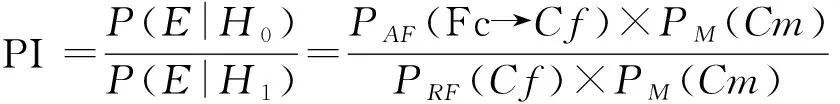
假定嫌疑父亲,母亲和孩子的基因型分别为(A,A), (C,D) and (D,E),等位基因A的频率为a,此时PI为：

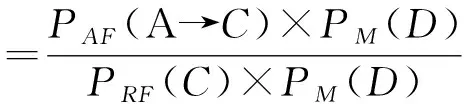
此种情况下对于特异突变率μ的估计显得尤为重要，由于上述情况中的μI→J突变的情况并不相同，可能以一步，两步，或更多步的形式突变，但是在实际的遗传过程中，却更有可能只是以一种形式突变。根据Brinkmann 等[11]在1万余例亲子鉴定中报告了23个突变，其中22个为一步突变，仅1个为2步突变。Brenner[13]给出了种简单合理更适用于STR的计算原则:

1)总体突变率μ近似代替一步突变率，μ(1/10)n-1近似代替多步突变率，其中n代表突变步数。

2)对于具体的情况考虑突变的方向性，突变率可以近似的认为是(1/2)μ。

3)μ近似代替男性突变率而女性突变率为μ/3.5。

但是他并没有给出这种计算方法的全部计算公式，同时，这种计算模型并不是静态的，2002年，Dawid给出了突变情况下的所有可能计算公式并举例说明了这些计算公式[14]。这些计算公式考虑到了可能发生突变的所有情况，用字母表示为18种不同形式的组合，每种组合都包含相对应的计算公式。该计算模型根据人群等位基因频率，突变步数等对总体突变率进行调整，具备静态性特点，即该模型可使群体基因频率在遗传过程中保持相对稳定。此外，其它典型的静态突变计算模型还包括[15-16]。最近Slooten K等发现STR位点存在一种“隐形突变”即突变的实际步数大于观察到的步数。对此进行考虑，利用贝叶斯定理根据总体突变率，性别，突变步数给出了一种估算特异突变率的新方法[17]。

3 总结

目前，贝叶斯计算理论已广泛应用于亲子鉴定过程中，用于对DNA分型结果进行量化，通常手工计算容易出错，因此利用计算机程序语言开发适合的计算程序代替手工计算是必要的[18]。此外，也可将嫌疑人DNA数据与犯罪人员DNA数据库中基因分型数据通过“标准三联体”进行比对，利用贝叶斯理论进行分析[19-20]。

本文对亲子鉴定过程中几种典型的情况下，如何应用贝叶斯理论计算亲权指数进行了描述，总体来讲，某些方面上仍需改进，例如：位点特异突变率估算不够精确，同时难以处理一些特殊情况例如Y染色体等。随着DNA相关技术的不断完善，人们对DNA物质各种现象认识的不断深入。相关算法的将不断精确化，可以更好地满足鉴定的需求。

[1] Essen-Möller E.Die Beweiskraft derhnlichkeit im Vaterschaftsnachweis-theoretische Grundlagen[J].Mitt Anthrop Ges,1938,68(Spec No):9-53.

[2] Ihm P.Die mathematischen Grundlagen, vor allem für die statistische Auswertung des serologischen und anthropologischen Gutachtens.in:K Hummel Ed.Die medizinische Vaterschaftsbegutachtung mit biostatistischem Beweis[M].Stuttgart:Fischer, 1961:128-145.

[3] Gürtler H.Principles of blood group statistical evaluation of paternity cases at the University Institute of Forensic Medicine Copenhagen[J].Acta Med Leg Soc,1956,9(Spec No):83-93.

[4] Ihm P.The problem of paternity in the light of decision theory.in:K Hummel, J Gerchow Eds.Biomathematical Evidence of Paternity[M],Berlin:Springer-Verlag, 1981:53-68.

[5] 阙庭志,张素华,赵书民.三联体亲权指数的统一算法及其扩展应用[J].法医学杂志,2011,27(5):334-336.

[6] Li CC, Chakravarti A.Basic fallacies in the formulation of the paternity index[J].Am J Hum Genet,1985,37(4):809-818.

[7] Elston RC.Probability and paternity testing[J].Am J Hum Genet, 1986,39(1):112-122.

[8] Baur MP, Elston RC, Gürtler H,et al.No fallacies in the formulation of the paternity index[J].Am J Hum Genet,1986,39(4):528-536.

[9] Mickey MR, Gjertson DW, Terasaki PI.Empirical validation of the Essen Moller probability of paternity[J].Am J Hum Genet,1986, 39(1):123-132.

[10] 陆惠玲，杨庆恩，侯一平.双亲皆疑亲子鉴定STR分型亲权指数计算方法探讨[J].中国法医学杂志，2001，16(4):210-212.

[11] Brinkmann B, Klintschar M, Neuhuber F, et al.Mutation rate in human microsatellites:influence of thestructure and length of the tandem repeat[J].Am J Hum Genet,1998,62(6):1408-1415.

[12] Henke L,Henke J.Mutation rate in human microsatellites[J].Am J Hum Genet,1999,64(5):1473-1474.

[13] Brenner C.Mutations in paternity[EB/OL].[2006-12-08].http://dna-view.com/mudisc.htm

[14] Dawid AP, Mortera J, Pascali VL, Non-fatherhood or mutation? A probabilistic approach to parental exclusion in paternity testing[J].Forensic Sci Int,2001, 124(1):55-61.

[15] Durret R, Kruglyak S, A new stochastic model of microsatellite evolution[J].J Appl Probability,1999,36(4):621-631.

[16] Egeland T，Mostad PF.Statistical genetics and genetical statistics:a forensic perspective[J].Scand J Stat,2002, 29(2):297-308.

[17] Slooten K, Ricciardi F.Estimation of Mutation Probabilities for Autosomal STR Markers[J].Forensic Sci Int Genet,2013,7(3):337-344.

[18] 施识帆,潘猛,冷锴,等.浅谈信息化技术在亲权鉴定中的应用[J].江苏卫生事业管理,2013,1(1):107-108.

[19] 巴华杰,刘亚楠,张璐,等.DNA数据库“标准三联体”亲缘关系比中应用价值初探[J].中国刑警学院学报,2012,1(1)：57-59.

[20] 葛建业,严江伟,Bruce B,等.关于法庭科学DNA数据库若干问题的探讨[J], 中国法医学杂志,2011.26(3):252-255.