复合函数极限法则的一个注记
2014-09-17 06:54李卫峰
大学数学 2014年6期
李卫峰
(中国地质大学 数学与物理学院,武汉 430074)
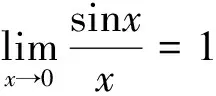

则



上述反例正是不满足“x≠0时g(x)≠0”这一条件所导致的.
定理1的一个重要应用是证明反函数导数定理.文献[2]中定理4.3就是对这进行讨论.

证给x=φ(y)的自变量y一个增量Δy,则Δx=φ(y+Δy)-φ(y),由反函数的连续性定理可知Δy→0时,必有Δx→0且Δy≠0时,Δx≠0.现在考虑
所以我们应当考虑极限
但注意到x=φ(y),y+Δy=f(x+Δx),所以Δy=f(x+Δx)-f(x),所以
上述关键在于上式中用到了复合函数的极限法则,即用到了定理1. 因为Δx→0时Δy→0.且Δx≠0时,Δy≠0.而且其中将Δy看成了Δx的函数.

[参 考 文 献]
[1] 同济大学数学系. 高等数学[M]. 北京:高等教育出版社,2007:48-49.
[2] 赵晶,彭放. 工科数学分析[M]. 武汉:中国地质大学出版社,2010:138-139.
猜你喜欢
语数外学习·高中版上旬(2022年6期)2022-07-23
农业资源与环境学报(2021年4期)2021-07-30
青年生活(2020年19期)2020-10-14
少儿美术(快乐历史地理)(2020年2期)2020-06-22
安全(2020年3期)2020-04-25
科学中国人(2018年8期)2018-07-23
读与写·教育教学版(2017年10期)2017-11-10
校园英语·下旬(2017年11期)2017-10-31
校园英语·中旬(2017年9期)2017-09-06
中学数学杂志(初中版)(2016年5期)2016-11-01

