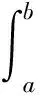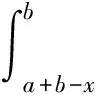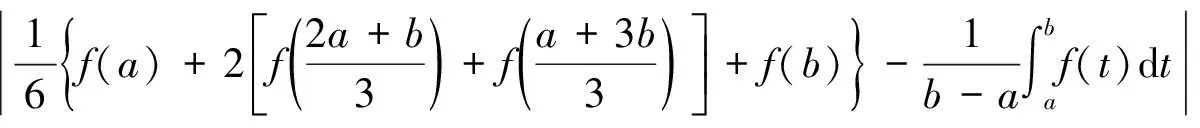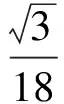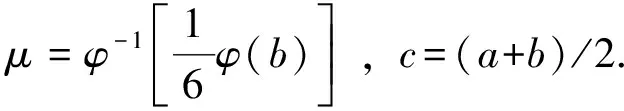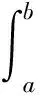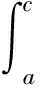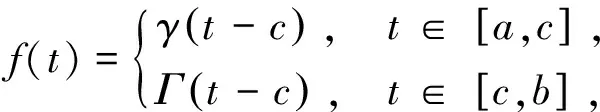两个严格的加权Ostrowski型不等式
时统业, 吴 涵, 周国辉
(海军指挥学院 信息系,江苏 南京 211800)
1 引 言
设f∶[a,b]→是(a,b)上的四阶连续可微函数,且则有
上述不等式称为Simpson不等式[1].
设f∶I⊂→是I°上的可微函数,a,b∈I°,a 上述不等式称为Ostrowski不等式[2]. 文[3]给出Simpson不等式的如下改进: 定理A[3]设f∶[a,b]→为连续函数,且f′∈L2(a,b),则 (1) 文[4]给出不等式(1)的带有一个参数的推广. 文[5]将不等式(1)推广到高阶可微函数,文[6-7]对有界变差函数给出加权的Simpson型不等式.已有许多文献给出Ostrowski不等式的推广和改进,这里仅推荐对作者启发较大的文献[3,8-10]. 本文给出一个新的严格的加权Ostrowski型不等式,在特殊情况下,由本文的结果可得定理A的一个加权推广. 引理1设f∶[a,b]→为连续函数,且f′∈L1(a,b),g(t)是[a,b]上正的可积函数,则对任意x∈[a,(a+b)/2],有 (2) 其中 证由分部积分法得 (3) (4) (5) 式(3),(4),(5)相加得式(2). 引理2[11](Grüss不等式的变式) 设h,g∶[a,b]→是两个可积函数,存在常数φ和Φ使得对任意x∈[a,b]有φ≤g(x)≤Φ,则有 定理1设f∶[a,b]→为连续函数,且f′∈L2(a,b),g(t)是[a,b]上正的可积函数,且关于t=(a+b)/2对称,则对任意x∈[a,(a+b)/2]有 (6) 其中 对于给定的区间[a,b]和给定的满足定理1条件的函数g(t),常数I是最佳的,即不能被更小的常数代替. 证由h(t)的定义、分部积分法及g(t)的对称性得 故有 (7) 由Cauchy积分不等式得 (8) 由h(t)的定义得 =I+Δ. (9) 在式(9)的推导中使用了下面事实: 由式(2),(7),(8),(9)得式(6). 下面证明对于给定的区间[a,b]和满足定理1条件的函数g(t),常数I是最佳的.假设常数C使得对于满足定理1条件的任意函数f(t)和任意x∈[a,(a+b)/2],都有 (10) 取函数 则f(t)在[a,b]连续且分段可导. 利用g(t)的对称性得 f(a)=f(b)=0, (11) (12) 易知 (13) 由f(t)的定义,经过计算得 (14) 其中式(14)的推导使用了下面事实: 于是使用式(11-14)得 推论1.1设f∶[a,b]→为连续函数,且f′∈L2(a,b),则对任意x∈[a,(a+b)/2],有 (15) 证在定理1中取g(t)≡1,则计算可得 由式(6)得到式(15).下面证明常数1/108是最佳的.假设常数C使得不等式 (16) 对于任意满足推论1条件的f(t)和任意x∈[a,(a+b)/2]都成立.取函数 则f(t)在[a,b]上连续,且分段可导,并且 又由定理1的证明可知式(16)的右端等于 所以式(16)也即 由此得C≥1/108,即常数1/108是最佳的. 推论1.2在定理1中,取x=(a+b)/2得 其中 常数I是最佳的,即不能被更小的常数代替. 特别地,当g(t)≡1时I=(b-a)3/36,Γ=0,由推论2得到定理A. 推论1.3在定理1中取x=a得 其中 定理2设f∶[a,b]→为连续函数,且f′∈L2(a,b),g(t)是[a,b]上正的可积函数,且关于t=c对称,x∈[a,c],φ(t)=g(τ)dτ,t∈[a,b].若存在常数γ和Γ使得对任意t∈[a,b]有γ≤f′(t)≤Γ,则有 (17) 证由引理2得 (18) 其中用到下面事实 不妨设 则有 (19) (20) 当x∈[a,μ]时, (21) 当x∈(μ,c]时, (22) 综合式(18-22)得式(17). 下面说明不等式(17)是严格的.事实上,当x∈[a,μ]时,取函数 则f(t)满足定理2条件,且式(17)的等号成立.当x∈(μ,c]时,取函数 则f(t)满足定理2条件,且式(17)的等号成立. 推论2.1设f∶[a,b]→为连续函数,且f′∈L2(a,b),g(t)是[a,b]上正的可积函数,且关于t=(a+b)/2对称.若存在常数γ和Γ使得对任意t∈[a,b]有γ≤f′(t)≤Γ,则有 (17) 式(17)在x=(2a+b)/3时取得最好结果: 证在定理2中取g(t)≡1得证. 推论2.2在定理2的条件下有 (17) 证在定理2中取x=c得证. [参 考 文 献] [1] Dragomir S S,Agarwal R P,Cerone P.On Simpson′s inequality and applications[J]. J.of Inequal.Appl.,2000, 5(6):533-579. [2] Ostrowski A.Über die Absolutabweichung einer differentiierbaren Funktion von ihrem Integralmittelwert[J]. Comment. Math.Helv.,1938,10(1): 226-227. [4] Liu Z.Note on a paper by N. Ujevi[J].Applied Mathematics Letters,2007,20(6):659-663. [5] Shi Y X, Liu Z. Some sharp Simpson type inequalities and applications[J].Applied Mathematics E-Notes,2009,9(7):205-215. [6] Tseng K L,Yang G S, Dragomir S S.On weighted Simpson type inequalities and applications[J].J.Math Inequal.,2007,1(1):13-22. [8] Tseng K L,Hwang S R,Dragomir S S.Generalizations of weighted Ostrowski type inequalities for mapping of bounded variation and their applications[J].Computers and Mathematics with Applications,2008, 55(8):1785-1793. [9] Tseng K L,Hwang S R,Yang G S,etal.Weighted Ostrowski integral inequality for mappings of bounded variation[J].Taiwanese Journal of Mathematics,2011,15(2):573-585. [10] Alomari M W.A companion of Dragomir′s generalization of Ostrowski′s inequality and applications in numerical integration[J].RGMIA Res.Rep.Coll., 2011(14), Article 50. [11] Cheng X L,Sun J. A note on the perturbed trapezoid inequality[J].J.Inequal.Pure Appl. Math.,2002,3(2),Article 29.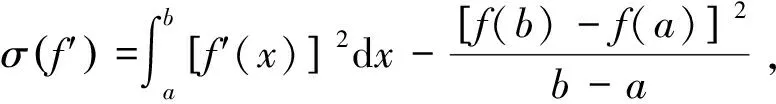

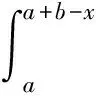

2 主要结果