关于连续总体秩统计量概率分布的递推公式
刘文丽, 吕书龙
(福州大学 数学与计算机科学学院, 福建 福州 350116)
1 引 言
假设检验是统计中常见的一种解决问题的手段.很多的实际问题要通过非参数假设检验加以解决.众所周知,非参数假设检验的一个核心问题是构造与秩有关的统计量,如检验对称性的符号秩统计量W+,揭示非线性相关性的Spearman和Kendall相关系数等.一般的教材会给出固定的分位数表来确定检验临界值,进而对检验作出判断[1-4],但极少会涉及这些统计量的构造、分位点和概率的计算问题.文献[5]提出了计算W+概率的一种多项式方法.但是随着样本量n的增大,这些秩统计量的概率和分位点的计算变得极为困难,目前常见的做法是通过统计量的渐进正态分布来取得所需的近似结果[1].
本文从秩统计量的构造出发,导出秩统计量与排列组合的等价关系,进而提出秩统计量概率分布的一种递推公式.递推公式很容易转成递归函数,因此容易编程实现,也便于教学上的理解和实际应用.
2 定义和性质
假设x1,x2,…,xn是来自总体X的一个样本,为讨论方便,设总体X服从某一连续分布.
定义1设xi各不相等,从小到大排序成x(1) 定义2设|xi|各不相等,以绝对值从小到大排序成|x(1)|<|x(2)|<…<|x(n)|. 若|xi|=|x(Ri)|, 则称xi的绝对秩为Ri,其中Ri=1,2,…,n. (1) (2) 其中tn(d)表示从1,2,…,n这n个数中任取若干个数(包括0个),其和恰为d的取法种数. 对于假设检验问题,H0:总体X的对称中心为原点.当H0成立时,W+的分布关于n(n+1)/4对称,且当n充分大时,W+服从N(n(n+1)/4,n(n+1)(2n+1)/24)的渐进正态分布. 定义3设样本x1,x2,…,xn来自总体X,样本y1,y2,…,ym来自总体Y,记N=n+m,并记xi在合样本x1,x2,…,xn,y1,y2,…,ym中的秩(依定义1)为R(i),R(i)=1,2,…,N.称总体X的样本的秩和 (3) 为Wilcoxon秩和统计量. 性质2对于假设检验问题,H0:FX(x)=FY(y).当H0成立时,Wx的分布律的等价形式为 (4) 其中tN,n(d)表示从1,2,…,N这N个数中任取n(n -n(n-1)/2≤d≤n(n-1)/2, sign(·)为通常的符号函数. 性质3Sn(d)取值满足对称性,即Sn(d)=Sn(-d). 显然任意一种排列r1,r2,…,rn都存在其逆序排列rn,rn-1,…,r1,则自然有Sn(d)=Sn(-d). 关于W+和Wx的渐进分布和近似计算以及检验分位点表,可参考文献[1,4].通过上述W+,Wx和Kendall-τ秩相关系数的构造和性质分析,本文给出求解其精确概率分布的递推公式,便于通过手工推导或编写程序得到精确的概率分布和检验分位点表. 由(2)式知tn(d)表示从1,2,…,n这n个数中任取若干个数(包括0个)其和恰为d的取法种数.由递推思路可将tn(d)分解成两部分之和: (a) 从1,2,…,n-1这n-1个数中任取若干个数(包括0个),其和恰为d的取法种数; (b) 固定含有n时,从1,2,…,n-1中任取若干个数(包括0个)的和恰为d-n. 由此可得tn(d)的递推公式 tn(d)=tn-1(d)+tn-1(d-n). (5) 若令N=n(n+1)/2,结合对称性质和d的特殊取值情况,将(5)式细化如下: 上述细化描述很容易编程实现,下面以求解t6(d)为例,给出手工推导过程,见表1. 表1 t6(d)的递推表格 当n=6时,易知d∈[0,1,2,…,21],由上述递推公式可以容易算出所有可能取值的取法种数,以d=10为例,有 t6(10)=t5(10)+t5(4)=t4(10)+t4(5)+t4(4)=t3(0)+t3(1)+t3(4)+t3(5)+t3(6)=5. tn(d)的推导层层递归,执行效率低,速度慢.因此在n较大时,P(W+≤d)宜采用渐进正态分布来实现.此处n多大算较大呢?这可从精确算法和近似算法的计算结果加以比较得到,参见表2. 表2 P(W+≤d) 从表2看出,递推公式较正态近似计算的精度要高许多.当n≥50时,基于正态分布和递推公式计算的结果虽然在数量级上偏差较大,但在实际应用中这个偏差基本全可以忽略.因此,我们认为在非参数检验的实际应用中,如果n≥50则可认为样本量较大,宜采用渐进正态分布进行近似计算,而当n<50时,宜采用精确分布进行计算. 由性质2知tN,n(d)表示从1,2,…,N这N个数中任取n个数,其和恰为d的取法种数.由递推思路可将tN,n(d)分解成两部分之和: (a) 从1,2,…,N-1这N-1个数中任取n个数,其和恰为d的取法种数; (b) 固定含有N时,从1,2,…,N-1中任取的n-1个数的和恰为d-N. 由此可得tN,n(d)的递推公式 tN,n(d)=tN-1,n(d)+tN-1,n-1(d-N). (6) 类似3.1,递推公式(6)很容易编成递归程序,进而求解P(Wx=d),P(Wx≤d)和分位点等.同样当n较大时,宜采用渐进正态分布来实现近似计算.表3给出递推公式和渐进分布的计算结果,同样看出当N,n较小时,两者存在明显的偏差. 表3 P(Wx≤d) 由性质3知Sn(d)表示对1,2,…,n这n个数随机排列后任意两个前后位置对应的数值差的符号和恰为d的排列种数.由递推思路可将Sn(d)等价成: 将n这个数插入到1,2,…,n-1这n-1个数任意排列后留出的n个位置中.对于n-1个数的排列,由于n这个数的插入位置不同,其满足的符号和的条件也不同. 例如n插入到第i个位置,则其对符号和的贡献中,前i-1为正,后n-i个为负,即贡献和为2i-n-1,即只要这n-1个数的排列满足符号和为d-2i+n+1就可实现递推.由此得Sn(d)的递推公式为 (7) 本文从排列组合角度将非参数秩统计量转化为等价的离散数列分布的研究,推导了秩统计量的精确概率分布的递推公式,给出了计算三类常用秩统计量概率的一种方法.递推结构清晰,实现方便,不足之处在于递归实现的时空复杂度较高.如何快速精确地计算秩统计量的概率分布,有待进一步研究. [参 考 文 献] [1] 王静龙,梁小筠. 非参数统计分析[M]. 北京:高等教育出版社, 2006. [2] 吴喜之,王兆军. 非参数统计方法[M]. 北京:高等教育出版社, 1996. [3] 陈希孺,方兆本,李国英,等. 非参数统计[M]. 上海:上海科学技术出版社,1989. [4] Conover W J.实用非参数统计[M]. 崔恒建译.北京:人民邮电出版社,2006. [5] 罗剑锋,赵耐青. 配对符号秩检验确切概率的递推算法[J]. 复旦学报(医学版),2004,3(31):274-276.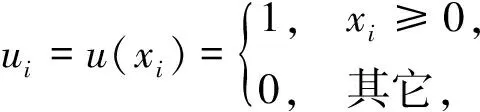


3 递推公式的构造
3.1 关于tn(d)的递推公式


3.2 关于tN,n(d)的递推公式

3.3 关于Sn(d)的递推公式
4 结 论

