《概率论与数理统计》应用实例选讲

许 静， 苏燕玲

(对外经济贸易大学统计学院，北京100029)

《概率论与数理统计》是一门研究和探索客观世界随机现象规律的数学学科，它以随机现象为研究对象, 在经济、管理、金融、保险等领域都有非常重要的作用.随着计算机科学的发展，以及功能强大的统计软件的开发，这门学科得到了蓬勃的发展，在自然科学和社会科学的各个领域应用越来越广泛.然而在学习中，学生普遍学习目的不明确，感觉学习困难，尤其不清楚该门课的应用领域.针对课程中的有关内容，穿插讲解一些应用实例会激发学生的学习兴趣，使教学内容不再枯燥、抽象，并能帮助学生加深对书本知识的理解，拓宽知识面，为其后续专业课的学习奠定良好的基础.

1 频数的应用—洛伦茨曲线

图1 洛伦茨曲线

在社会经济调查中，经常得到的数据是频数，洛伦茨曲线是累积频数的典型应用[1].将居民收入按从低到高排列，各收入等级的家庭的累积百分比为横坐标，与之相对应的收入的累积百分比为纵坐标，得到的曲线就是西方经济学中著名的洛伦茨(Lorentz M E)曲线，如图1所示.

图1中，直线OM为绝对平等线，在这条线上，每10%的人得到10%的收入，表明收入分配完全平等.OPM表明收入分配极度不平等，全部收入集中在1个人手中，称为绝对不平等线.介于二线之间的实际收入分配曲线就是洛伦茨曲线.洛伦茨曲线与绝对平等线OM越接近，收入分配越平等；与绝对不平等线OPM越接近，收入分配越不平等.

基尼系数是20世纪初意大利经济学家基尼根据洛伦茨曲线提出的判断分配平等程度的指标.设表示实际收入分配的洛伦茨曲线和收入分配的绝对平等线之间的面积为A，洛伦茨曲线右下方的面积为B，基尼系数是用A除以(A+B)的商，表示不平等程度.如果A为零，基尼系数为零，表示收入分配完全平等；如果B为零则基尼系数为1，收入分配绝对不平等，故该系数在0和1之间取值.收入分配越是趋向平等，洛伦茨曲线的弧度越小，基尼系数也越小. 反之，收入分配越是趋向不平等，洛伦茨曲线的弧度越大，那么基尼系数也越大.基尼系数的具体计算还应参考有关文献[2].

国际上通常用基尼系数来判定收入分配均等程度.市场经济国家衡量收入差距的一般标准为：基尼系数在0.2以下表示绝对平均；0.2-0.3之间表示比较平均；0.3-0.4之间表示较为合理；0.4-0.5之间表示差距较大；0.5以上说明收入差距悬殊.国际上通常把0.4作为收入分配差距的“警戒线”.一般发达国家的基尼指数在0.24到0.36之间.2013年1月，国家统计局发布了2003-2012年中国内地居民收入的基尼系数，依次为0.479，0.473，0.485，0.487，0.484，0.491，0.490，0.481，0.477，0.474，均已超过0.4的警戒线.基尼系数过大会带来一系列的社会问题，应引起各方面的关注.基尼系数在经济工作中可以作为一个综合经济参数纳入国家的计划管理和宏观调控之中.

2 正态分布标准差的应用— 6σ管理

6σ(6SIGMA)管理，最早由摩托罗拉(Motorola)公司提出，后来由于通用电气(GE)的积极推行，并取得市场价值第一的卓越业绩，使6σ管理的理论逐渐完善，并且应用实践不断推广.

通常把生产流程或服务流程抽象为一条正态曲线[3]，设某质量特性X～N(μ,σ2)，其特性值落在μ两侧各6σ之外的概率为

P{|X-μ| >6σ}=2-2Φ(6) =0.000000002

即十亿分之二，这是一个小概率事件，通常在一次试验中是不易发生的，一旦发生就认为流程质量发生了异常.通常当考虑到1.5σ系统偏移[4](右偏或左偏)的影响后，质量特性值超出规格上下限的不合格率就约等于百万分之(ppm)3.4，即每百万次机会中只有3.4个缺陷数，这正是6σ管理所采用的计算方法.作为一种衡量标准，σ的数量越多，质量就越好.表1给出的是对美国企业的4σ质量水平和6σ质量水平的对比，可以看出从4σ质量提高到6σ质量的意义.

表1 4σ和6σ质量水平的对比

6σ管理的基本原则是：提高顾客满意度和降低资源成本,6σ管理逐步发展成为以顾客为主体来确定企业战略目标和产品开发设计的标尺，追求持续进步的一种质量管理哲学.

3 随机变量函数分布的应用—产生随机样本

对于一元连续型随机变量有这样的结论：设连续型随机变量X的分布函数是F(x)，则随机变量Y=F(X)服从区间(0,1)上的均匀分布.

只要X是连续型随机变量，无论服从什么分布，上述结论都是成立的.反之，若Y服从(0,1)上的均匀分布，对满足条件的分布函数F(x) ，令X=F-1(Y)，则X的分布函数就是F(x) .这个结论在随机模拟中起重要作用，只要能产生(0,1)上的均匀分布的随机数y，就能通过x=F-1(y) 产生服从分布函数为F(x)的随机变量的样本.

常用办公软件Excel的随机数生成器可以生成均匀分布、正态分布、伯努利分布、二项分布、泊松分布的随机数，却无法生成其它一些常用分布的随机数，而利用上面的概率知识能够方便地得到诸如指数分布这样的常用分布的随机样本.

例如，设随机变量X服从参数为1的指数分布，其分布函数为

令Y=1-e-X，则Y服从区间(0,1)上的均匀分布.若要随机模拟X的一个容量为10的样本，可以先用Excel的随机数生成器产生服从区间(0,1)上的均匀分布的一个容量为10的样本，记做y1,y2,…,y10,如下

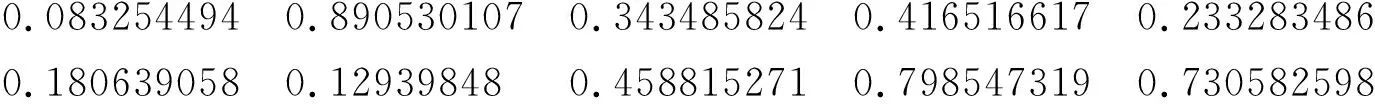
令xi=-ln(1-yi),i=1,2,…10,即得到服从参数为1的指数分布的一个容量为10的样本

利用这样的模拟数据就可以进行有关指数分布的研究了.

4 期望的应用——最优决策

数学期望刻画了随机变量取值的加权平均，是随机变量的一个重要数字特征.最优期望决策是一种常用的风险决策，它根据各可选方案的收益(或损失)的期望值的大小选择最优方案.例如，某人有10万元现金，有三种投资方式A，B，C，如想得到最大收益，他应该选择哪种投资方式？表2给出三种投资方式在一年中的投资成功的概率和获利额，以及投资失败的损失额.

表2 三种投资方式的对比

设A，B，C三种投资方式的收益分别为X，Y，Z，计算它们的数学期望，得

收益期望最大的是投资方式B，故应该选择B.

决定各方案取舍的决策标准不同，会产生不同的决策结果. 例如，有时需要控制损失量，就应选择损失的期望达到最小的方案.

5 置信区间的应用——风险价值

风险价值VaR (Value at Risk)是指资产或负债暴露于风险中的部分，是目前市场上最流行、最为有效的风险管理技术.其常规的定义是：在正常市场条件下和一定置信水平(如99%或95%)下计算出的给定时间段内预期发生的最大价值损失量.VaR的数学表达式为

P{X≥-VaR}=1-α，

其中X表示投资或证券组合在持有期t内的收益，X不低于-VaR的概率是1-α，说明损失大于VaR的概率为α，即

P{X<-VaR}=α.

例如，MorganJ P公司1994年年报披露[5]，1994年该公司一天的95%的VaR是1500万美元，其含义是，该公司可以以95%的概率保证，在1994年每一特定的时点上的证券组合在未来的24小时内，由于市场波动而带来的损失不会超过1500万美元.

计算VaR需要三个量，置信水平1-α，持有期限t，收益X的概率分布函数F(x)，核心是确定F(x).一种确定F(x)的方法是参数法：假设X服从正态分布，然后估计其中的参数，从而确定X的分布.不同的方法，有不同的估计结果，可以参阅有关的文献.

VaR方法已经在风险度量、风险控制、风险监管、绩效评估等方面发挥着重要的作用，是企业进行全面风险管理和运用收益风险比率进行战略决策的工具和方法.许多银行、经纪公司和基金公司都使用VaR去度量它们所面临的市场风险，金融监管者也使用VaR作为其管理的标准.

6 其 它

概率论与数理统计中还有很多内容可以在教学中结合经济、管理、保险、金融等学科的例子进行讲解，例如证券投资的收益与风险，证券组合的投资分析，保险中保额的统计分析，保费与理赔量的统计分析，经济、人口等的预测分析等.

[参 考 文 献]

[1] 何晓群.现代统计分析方法与应用[M].北京：中国人民大学出版社，1998:21-22.

[2] 龚志民，胡志军.基尼系数计算的误差估计与中国居民收入差距分析[J].统计研究，2010,27(3):107-109.

[3] 何晓群.关于6Sigma与3Sigma的比较[J].数理统计与管理,2006, 25(2): 175-177.

[4] 张建方，宗福季.关于6Sigma管理中的1．5Sigma系统偏移[J].数理统计与管理,2004, 24(6): 10-18.

[5] 王春峰, 万海晖, 张维.金融市场风险测量模型—VaR[J].系统工程学报,2000，15(1):67-75.