线性矩阵不等式及其在细胞神经网络保性能控制中的应用

江 梅， 何汉林

(海军工程大学理学院，湖北武汉430033)

1 引 言

1988年由Chua和Yang[1]首次提出的细胞神经网络(CNNs)模型，是当前最流行、研究最广泛的人工神经网络之一.由于其神经元间局部连接的特点，使得在超大规模集成电路(VLSI)实现中，能输出分段函数信号，且运行速度较快.细胞神经网络在图像处理、模式识别、优化控制、联合存储等诸多领域得到了广泛应用.细胞神经网络中包括了饱和的非线性单元，因此关于饱和非线性系统的研究更为重要.而神经网络中存在时滞现象是很普遍的，诸如信号传递时滞、细胞时滞、突触时滞等，这些时滞可能会导致神经网络失去稳定性.1990年，Chua和Roska提出时滞细胞神经网络(DCNN)概念，状态方程为

(1)

在过去几十年里，一些学者运用Lyapunov-Krasovskii定理、Lyapunov-Razumikhin定理、线性矩阵不等式(LMI)技巧及随机分析方法等提出了诸多针对时滞细胞神经网络的稳定准则[2-4].保性能控制方法就被引用到了其中.保性能控制问题，主要针对具有参数不确定性的系统，通过控制律的设计，不仅使得闭环系统稳定，而且使得闭环系统的性能指标不超过某个确定的上界.运用LMI方法可设计保性能控制器并处理各种附加约束.

LMI凭借其优良性质广泛应用于控制系统分析和设计等领域，与Lyapunov方程和Riccati方程[5]相比，LMI不需要调整任何参数和对称正定矩阵，其通用性和可解性对时滞系统以及不确定时滞系统的研究具有十分重要的理论意义和应用价值.随着LMI的内点法的提出以及MATLAB软件中LMI工具箱的推出，LMI已成为系统与控制领域研究中的热门工具.LMI控制工具箱提供了在鲁棒控制设计中所遇到的凸最优化问题的解，同时给出了一个用于求解LMI的集成环境.用LMI技术求解控制问题，是目前和今后控制理论发展的一个重要方向.

本文介绍了LMI的相关概念和性质，对Schur补引理提出引理，将二次矩阵不等式(QMI)转化为线性矩阵不等式(LMI)，从而更好的应用于控制参数求解；提出了LMI的基本问题和MATLAB工具箱，并对LMI在细胞神经网络的保性能控制问题作出了简要描述.

2 线性矩阵不等式(LMI)的相关概念[6-7]

2.1 LMI描述

定义线性矩阵不等式的一般形式如下：

F(x)=F0+x1F1+…+xnFn<0，

(2)

其中F0，F1,F2，…,Fn是给定的实对称矩阵,x1,x2,…,xn是n个实数变量，称为线性矩阵不等式的决策变量，x=x1,x2,…,xnT∈n是由决策变量构成的向量，称为决策向量.F(x)<0表示F(x)负定，即对所有非零的向量α∈n，αTF(x)α<0.若F(x)≤0，则相应的矩阵不等式称为非严格的线性矩阵不等式.

多个LMI可用一个LMI表示，即F1(x)<0,F2(x)<0,…,Fn(x)<0等价于

diagF1(x),…,Fn(x)<0.

(3)

2.2 LMI性质

性质1凸性：Φ=x|F(x)<0是一个凸集.

对任意的x1,x2∈Φ，任意α∈(0,1)，由于Fx1<0,Fx2<0，F(x)是一个仿射函数，因此Fαx1+1-αx2=αFx1+1-αFx2<0.故αx1+1-αx2∈Φ，即Φ是凸的.

性质2有限个LMI凸集的交集也是凸集，并可以等价地用一个LMI表示.

设F1(x)<0,F2(x)<0，交集x|F1(x)<0∩x|F2(x)<0，也可表示为

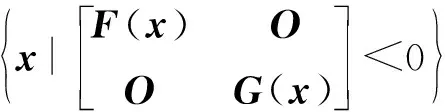
因为一个对称的块对角矩阵正定(半正定或负定)当且仅当它的对角块矩阵正定(半正定或负定).

2.3 引理

引理1(Schur补引理) 考虑一个矩阵X∈n×n，分块，下列三个条件等价：

(i)X<0;

(4)

其中X11∈r×r，X11和X22是对称矩阵，X12是变量x的仿射函数，称为X11在X中的Schur补.

Schur补引理的特点是可将一类凸非线性不等式转化为线性矩阵不等式，从而更方便进行求解.在控制理论中，主要常使用下列两种矩阵不等式：

(i) Lyapunov不等式

ATX+XA+Q<0；

(5)

(ii) Riccati不等式

ATX+XA+XBTBX+Q≤0,

(6)

其中X=XT∈n×n.易得式(5)是线性矩阵不等式，式(6)含有二次项XBTBX，故此式是二次线性矩阵不等式.利用Schur补引理，可将其变成线性矩阵不等式.即

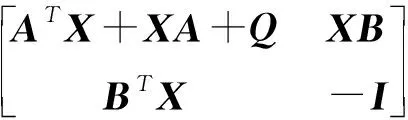
(7)

引理2[14]假设X22<0,D>0，下列二次矩阵不等式

(8)

成立当且仅当

(9)

其中X11∈p×p,X12∈p×q,X22∈q×q,H∈d×p,D∈d×d,,,DT=D.

引理2实际上是Schur引理的一个推广，即对一个含多个未知矩阵的矩阵不等式多次使用Schur引理.当X22<0时，可将一个二次矩阵不等式转化为线性矩阵不等式.

2.4 LMI工具箱的三个标准问题

基于内点法，Matlab软件开发出功能强大的LMI工具箱算法，这是求解一般线性矩阵不等式问题的一个高性能软件包.一旦确定线性矩阵不等式问题，即可通过调用三个标准LMI问题的求解函数对问题进行数值求解.

(i) 可行解问题(LMIP)： 给定一个形如(2)式的线性矩阵不等式，判断是否存在可行解xp使得线性矩阵不等式F(xp)>0成立.如果该LMI凸集非空，即xp存在，称该线性矩阵不等式是可行的；否则，该线性矩阵不等式不可行.其相应的MATLAB求解器是feasp.

(ii) 特征值问题(EVP)： 在LMI约束下将一个矩阵的最大特征值极小化.当A,B是变量x的对称矩阵.EVP问题等价于一个带有不等式约束的凸优化问题：

minλ, s.t.λI-A(x)>0,B(x)>0.

(10)

此问题在系统和控制理论中应用较多，相应的MATLAB求解器是mincx.

(iii)广义特征值最小化问题(GEVP)：在LMI约束下将一对方阵的广义最大特征值极小化.

形如

minλmaxA(x),B(x), s.t.B(x)>0,C(x)>0.

(11)

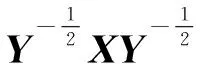
此外，该工具箱还可以用于综合多目标控制器设计，系统鲁棒性分析和检测，系统辨识、滤波、结构设计等问题.

3 LMI在细胞神经网络保性能控制中的应用

LMI方法给出了问题可解的一个凸约束条件，因此可应用求解凸优化问题的方法来求解LMI，无需预先调整任何参数和正定对称矩阵，大大降低了求解问题的保守性.基于LMI方法得到的结果大多是时滞依赖的，与时滞独立的设计方法相比，保守性较差.目前的研究方向是如何合理选择Lyapunov函数，通过适当的不等式变换，得到一个或者多个LMI来保证闭环系统的渐近稳定，且同时提高系统的性能.

由于LMI方法的高效求解方法，国内外学者将其广泛应用于保性能控制的研究.利用LMI方法，Yu Li[8]针对一类线性不确定时滞系统给出了保性能控制的研究，并给出了无记忆状态反馈保性能控制器的存在条件和设计方法.Guan[9]等研究了基于T-S模型的具有时滞依赖的保性能控制问题，Lien[10]研究了基于LMI的中立型变时滞系统的时滞独立和时滞依赖的保性能控制问题，用LMI求解稳定性问题，给出了控制器的设计方法.

由于细胞神经网络的时滞现象极其常见，且这些时滞很可能导致神经网络失去稳定，导致混沌现象，影响细胞神经网络的性能.在He[11-14]等近期的论文中，根据细胞神经网络的特点，将饱和激励函数通过大中取大方法转化为若干个顶点的控制问题，并根据Lyapunov-Krasovskii定理[11-12]、Lyapunov-Razumikhin定理[13-14]、利用引理2及合同变换、LMI技巧等理论提出了变时滞细胞神经网络的一类新型保性能混沌同步及镇定控制器，其中利用Razumikhin定理，可以去掉系统对时滞变化率上界的限制.文献[11-14]进一步利用线性矩阵特征值问题的最小化工具箱提出使细胞神经网络系统二次型性能指标式最小化问题的同步及镇定控制器的条件.通过仿真实例和计算得出的保性能函数上界的值及最小化保性能函数上界的值，文献[11-14]证实了保性能混沌同步及镇定控制器及最小化保性能混沌同步及镇定控制器的有效性.

在解决问题时，一般先将各个性能指标与其相应的LMI可解条件一一对应提出QMI，通过Schur补引理及引理2转化为LMI问题，再利用LMI的线性特性，把与各目标相对应的LMI组合成统一的约束框架，而后考虑二次性能函数：

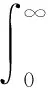
(12)

其中Q>0,R>0，J存在上界，主要目标是通过设计保性能控制律u(t)，最终使得细胞神经网络(1)全局渐近稳定.下面简要叙述保性能控制律的主要设计过程.

对矩阵X=(xij)n×n∈n×n，其第i列可表示为xi=(x1i,x2i,…,xni)T.令

其中vi=0或1.定义集合Φ=v∈n:vi=0或1，则集合Δ(v,X)含有2n个元素.

定理[14]基于(1)和(12)，若存在对称正定矩阵P∈n×n，矩阵K∈n×n，则对所有v,w满足

(13)

可找到一个控制律u(t)=-Kx(t)为全局保性能稳定控制律，使得(1)全局渐近稳定.

4 结 论

本文对线性矩阵不等式问题作出了简要描述，介绍了其中细胞神经网络中的保性能控制应用.文章讨论了其基本性质和几个标准的LMI问题，运用Schur补引理和引理2，从而将一个二阶矩阵不等式问题转化为线性矩阵不等式问题，介绍了在MATLAB控制工具箱中的功能和应用，并对LMI在细胞神经网络的保性能控制问题作出了简要描述.

[参 考 文 献]

[1] Chua L O, Yang L. Cellular neural networks: Theory [J]. IEEE Transactions on Circuits and Systems I, 1988, 35(10):1257-1272.

[2] Zheng C D, Zhang H G. Novel delay-dependent criteria for global robust exponential stability of delayed cellular neural networks with norm-bounded uncertainties [J]. Neurocomputing, 2009, 72(7-9): 1744-1754.

[3] Tan M C. Global asymptotic stability of fuzzy cellular neural networks with unbounded distributed delays [J]. Neural Processing Letters, 2010, 31(2):147-157.

[4] Akhmet M U, Arugaslan D, Yilmaz E. Stability in cellular neural networks with a piecewise constant argument [J]. Journal of Computational and Applied Mathematics, 2010, 233(9): 2365-2373.

[5] D’ Andrea R. Linear matrix inequality conditions for robustness and control design [J]. International Journal of Robust and Nonlinear Control, 2001, 11(6):541-554.

[6] Boyd S, Ghaoui L E, Feron E, et al. Linear Matrix Inequalities in system and control theory [M]. Philadelphia, PA: SIAM, 1994.

[7] Gahinet P, Nermirovski A. General-purpose LMI solvers with benchmarks [C]. Decision and Control, San Antonio, TX, 1993, 4: 3162-3165.

[8] Yu L, Chu J. An LMI Approach to Guaranteed Cost Control of Linear Time-delay Systems [J]. Automatica, 1999, 35(6):1155-1159.

[9] Guan X, Chen C. Delay-Dependent Guaranteed Cost Control for T-S Fuzzy Systems with Time Delays [J]. IEEE Transactions on Fuzzy System, 2004, 12(2):236-249.

[10] Lien C. Delay-Dependent and Delay-Independent Guaranteed Cost Control for Uncertain Neutral Systems with Time-Varying Delays via LMI Approach [J]. Chaos, Solutions & Fractals, 2007, 33(3): 1017-1027.

[11] He H, Yan L, Tu J. Guranteed cost stabilization of cellular neural networks with time-varying delay [J]. Asian Journal of Control, 2013, 15(4): 1224-1227.

[12] Tu J, He H, Xiong P. Guaranteed cost synchronous control of time-varying delay cellular neural networks [J]. Neural Computation & Application, 2013, 22(2): 103-110.

[13] He H, Yan L, Tu J. Guaranteed cost stabilization of time-varying delay cellular neural networks via Riccati inequality approach [J]. Neural Processing Letter, 2012, 35(2): 151-158.

[14] Tu J, He H. Guaranteed cost synchronization of chaotic cellular neural networks with time-varying delay [J]. Neural Computation, 2012, 24(1): 217-233.