分段低次插值多项式序列的一致收敛性
钱 江, 王 凡, 吴云标
(1.河海大学理学院, 南京210098; 2.南京农业大学工学院基础课部,南京210031; 3.河海大学文天学院基础部, 安徽马鞍山243031)
1 引 言
“一致收敛性”是函数列或函数项级数更强意义下的收敛性,强调的是所寻找的N=N(ε),与普通意义下的收敛性所寻求的N=N(ε,x)有本质的区别,这是初学者在学习数学分析[1]或高等数学A课程时容易困惑的一个知识点. 近年来,从教学目的出发,人们对函数列或函数项级数的一致收敛性问题进行了一些研究. 葛仁福[2]结合函数列与函数一致连续的性质,得到了函数列一致收敛的新判别法. 傅湧[3]利用函数列的等度连续性, 得出了若干有界闭区间上连续函数列一致收敛的充要条件, 推广了Dini定理. 张丽君[4]利用Abel变换等方法, 获得了复空间中三角级数在满足一定条件下一致收敛的充要条件. 周项平[5]给出了关于具有微少改变系数的三角级数一致收敛性的本质推广结果.
然而,函数列或函数项级数的一致收敛性所发挥的作用应不限于数学分析,如徐业基[6]改进和推广了平稳随机过程的采样定理,并求出了它的一致收敛速度及误差估计.这些关于一致收敛性与其它学科相联系的理论研究值得我们思考,这样不论是数学分析等基础课程还是其它课程教学都能让学生感受到这一概念的重要性. 故而,作者根据自身实际教学经验与学生学习困惑,考虑有关函数列与函数项级数“一致收敛性”在说明计算方法、数值分析[7]与数值逼近[8,9]课程中相关知识点起着怎样的作用?这些相关知识点主要包括Lagrange插值多项式序列是否一致收敛于被插函数、与插值型求积公式序列是否收敛于积分的真值等?本文主要研究分段低次插值序列一致收敛性问题,围绕如下问题展开.
问题1怎样条件下,插值多项式序列
pn(x)→→f(x),n→∞,x∈[a,b]?
问题2如何选取插值节点,使得
|w(x)|=|(x-x0)(x-x1)…(x-xn)|=min?
问题3设互异插值节点a=x0 定义2.1[1]设函数列fn(x)与函数f(x),x∈D,若∀ε>0,∃N(ε)∈, 使得当n>N时,对一切x∈D,都有 |fn(x)-f(x)|<ε, 则称函数列fn(x)在D上一致收敛于f(x), 记作 数值逼近[8,9]或数值分析[7]中,我们首先学习到的是完善的一元多项式插值理论. 由于考虑插值序列的一致收敛性,因此先给出插值余项. 定理2.1[7,9]设f(x)∈Cn+1[a,b],pn(x)为n+1个互异节点诸xi上的n次Lagrange插值多项式,则有插值余项 其中w(x)=(x-x0)…(x-xn),ξ∈(a,b). 由于插值多项式序列未必总是一致收敛于被插函数[8,9],如Runge现象,因此人们自然思考怎样条件下,插值多项式序列一致收敛于被插函数. 这问题的解决方法颇多,为避免高次插值可能出现的Runge现象,典型的处理方法:或选取Chebyshev零点作为插值节点,或利用分段低次插值取代高次插值. 定理2.2[8,9]设f(x)∈C2[-1,1], 插值节点取为Chebyshev零点 (2.1) 则在[-1,1]上pn-1(x)→→f(x),n→∞. 设互异插值节点a=x0 数值分析教材上从数值算例说明了分段低次插值的优越性,而未从理论上加以证明,这往往受教学内容与教学时间的制约.下面分析分段低次插值基函数性质,结合函数列一致收敛概念来研究分段低次插值序列的一致收敛性. 定理3.1[7]设f(xk)=fk,a=x0 I1,h=lk-1fk-1+lkfk,x∈[xk-1,xk], (3.1) 其中 (3.2) 注3.1 基函数满足单位分解性 lk(x)+lk+1(x)=1,x∈[xk,xk+1], (3.3) 且诸lk(x)≥0. I1,h→→f(x),n→∞. 证利用连续模定义: 与基函数的单位分解性,有 |f(x)-I1,h(x)| ≤lk(x)|f(x)-fk|+lk+1(x)|f(x)-fk+1| ≤(lk(x)+lk+1(x))|w(hk)|≤w(hk)≤w(h) ⟹I1,h→→f(x),h→0+, 且均匀剖分下结论显然成立. 若采用Lagrange线性插值余项公式证明[7],则需要条件f(x)∈C2[a,b]. 其中 (3.4) 注3.2 基函数性质: (3.5) 事实上,容易验证(3.5)的第一式;而对于其第二、三不等式,由(3.4)式不难求出βk(x),βk+1(x)的最大值,从而得证. 对区间均匀剖分与非均匀剖分时的分段三次Hermite基函数αk(x)分别如图1所示,每张图中的实线与虚线分别表示(3.4)式α(x)两部分曲线. 同时,对区间均匀剖分与非均匀剖分时的分段三次Hermite基函数βk(x)分别如图2所示,每张图中的实线与虚线分别表示(3.4)式β(x)两部分曲线. 图1 均匀(左)与非均匀(右)剖分上的分段三次Hermite基函数αk(x) 图2 均匀(左)与非均匀(右)剖分上的分段三次Hermite基函数βk(x) I3,h→→f(x),n→∞. 证利用连续模定义、Lagrange中值定理以及基函数的性质,有 ⟹I3,h→→f(x),h→0+. 均匀剖分下结论显然成立. 若采用三次Hermite插值余项公式证明[7],则需要条件f(x)∈C4[a,b]. [参 考 文 献] [1] 华东师范大学数学系. 数学分析(下册)[M].4版.北京:高等教育出版社, 2010. [2] 葛仁福. 函数列一致收敛判别法[J]. 大学数学, 2011, 27(4): 179-181. [3] 傅湧. 有界闭区间上连续函数列一致收敛的充要条件[J]. 大学数学, 2007, 23(3): 117-120. [4] 张丽君. 三角级数一致收敛性问题在复空间的完整推广[J]. 数学杂志, 2012, 32(3): 461-465. [5] ZHOU Songping. A Remark on the Uniform Convergence of Certain Trigonometrie Series[J]. 数学进展, 2007, 36(2): 239-244. [6] 徐业基. 关于平稳随机过程的采样定理的一致收敛速度[J]. 大学数学, 2009, 25(6): 48-51. [7] 李庆扬, 王能超, 易大义. 数值分析[M].5版. 北京:清华大学出版社, 2008. [8] 徐利治, 王仁宏, 周蕴时. 函数逼近的理论与方法[M]. 上海:上海科学技术出版社, 1983. [9] 王仁宏. 数值逼近[M]. 北京:高等教育出版社, 1999.2 一致收敛与插值序列
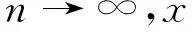
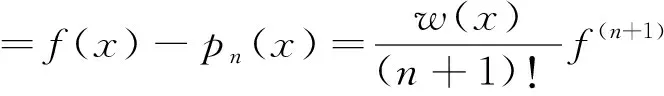
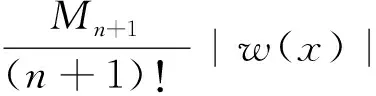

3 分段低次插值序列