磁控旋弧管板对焊激磁线圈径向磁场的简化算法

熊飞飞，包晔峰，朱修强，蒋永锋 ，杨 可

（1.河海大学 机电工程学院，江苏 常州213022；2.今创集团有限公司，江苏 常州 213022）

0 前言

磁控旋弧对焊通过在焊接电弧周围施加外部磁场，利用磁场力驱动电弧沿管状工件断面高速旋转，使工件断面均匀加热熔化，在快速顶锻力的作用下形成焊接接头[1]。旋弧对焊无需填充材料，焊接飞溅少，易于实现自动化，具有节约能源、焊接外形美观、生产效率高等优点[2]。磁场的空间分布是影响磁控旋弧管板对焊电弧旋转状态的重要因素之一。激磁电流大小、线圈结构和位置等决定磁场的分布状况，计算和分析外加磁场有助于更好地利用磁场分布控制电弧运动，提高焊接质量。

1 激磁线圈径向磁场简化算法

管板对焊时，激磁线圈产生的磁感应强度受内部铁磁工件和导磁机构的影响，完整的磁路分析和计算包含铁磁材料和非铁磁材料整个空间区域，考虑线圈内部磁芯和不同介质磁阻的管件径向磁感应强度的精确计算是非常困难的[3]。适当的假设可简化线圈径向磁感应强度的理论计算，简化算法是常用的工程手段。本研究选择空心圆柱轴对称线圈作为管板对焊的激磁线圈，为便于分析和计算，作以下假设：

（1）线圈的所有线匝均是同轴的圆形回路。

（2）线匝之间有无限薄的绝缘，所有线匝紧密地填充了线圈的全部空间。

（3）线圈线匝在径向、轴向均匀缠绕，电流沿截面均匀分布，而且电流密度的方向和对称轴的正向构成右手螺旋关系[4]。

磁控旋弧管板对焊时，激磁线圈在管件端面产生的磁场既有径向磁感应强度又有轴向磁感应强度，但只有径向磁感应强度才能与电弧作用产生驱动电弧旋转所需要的洛伦兹力。在此只分析和计算激磁线圈的径向磁感应强度。

如图1所示，设圆柱线圈匝数为n、激磁电流Ie、线圈的中心半径R。用线圈几何中心处的线匝代替整个激磁线圈，则流经线匝的电流为n匝线圈中电流的总和，即I=nIe。

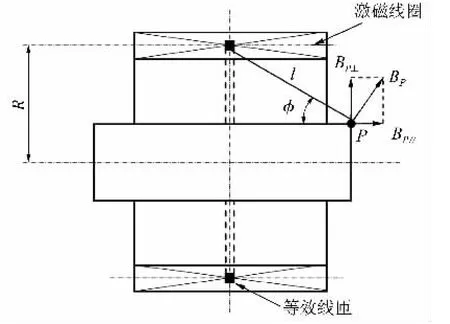
图1 管板对焊磁场计算示意

由于激磁线圈各电流元在管件端面产生的径向磁感应强度大小不等、方向也不同[5]，为了方便积分运算，用正六边形ABCDEF表示中心等效线匝的横截面，如图2所示，用六边形的各边代替整个圆弧，先分别求出各直线段对P点的磁感应强度，再用几何法进行合成，即可得到整个线圈在P点的磁感应强度。

根据毕奥-萨伐尔定律，在多边形的一边AB上取电流元Idl，则Idl在P点处产生的磁感应强度的大小可表示为

式中 μ0为真空导磁系数，μ0≈4π×10-7N/A2；m 为P点到电流元Idl的距离；θ为电流元Idl与PH间的夹角。

则AB在P点产生的磁感应强度大小为

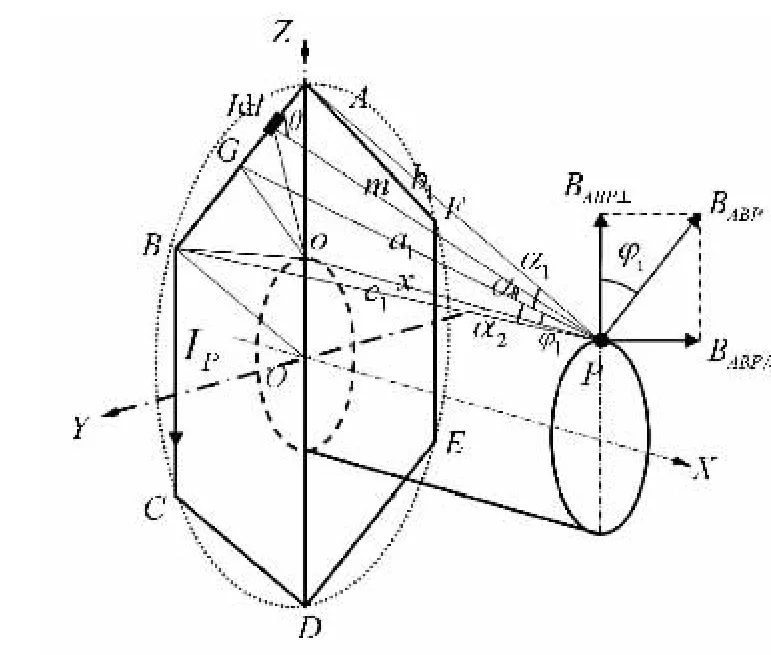
图2 磁感应强度的计算模型

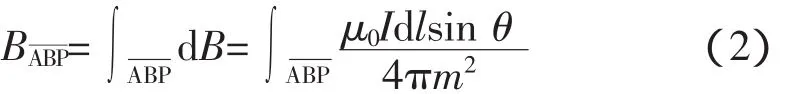
变量 l、m、θ与夹角 α 存在下列几何关系：sin θ=cosα；m=a1sec α；l=a1tan α；dl=a1sec2αdα。则 AB 在 P点产生的径向磁感应强度大小可表示为

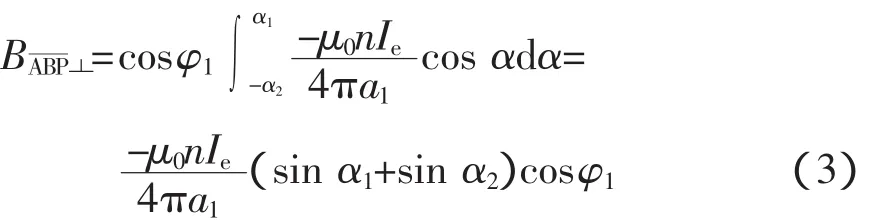
在RT△AOP中（见图2）

在△ABO 中，∠BAO=60°，AB=AO′=BO′=R，由余弦定理可求得

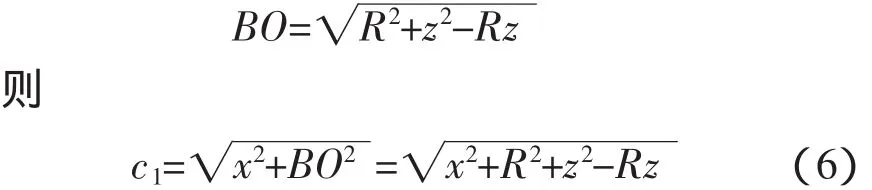
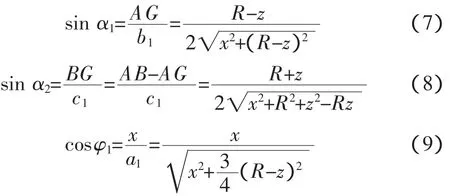
由以上数据可得

将式（7）～式（9）代入式（3）得出 AB 在 P点的径向磁感应强度大小为

同理，可以得出CD在P点的径向磁感应强度大小为

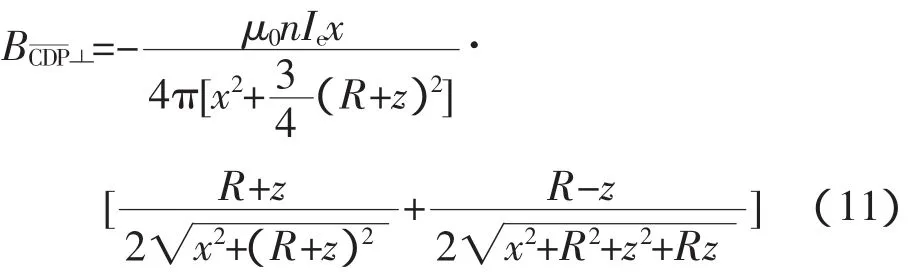
如图3所示，线段和对称和对称，所以 BAFP┴=BABP┴，BDEP┴=BCDP┴。由于线段和在P点产生的径向磁感应强度BCDP┴和BEFP┴大小相等、方向相反，因此两者可以相互抵消。

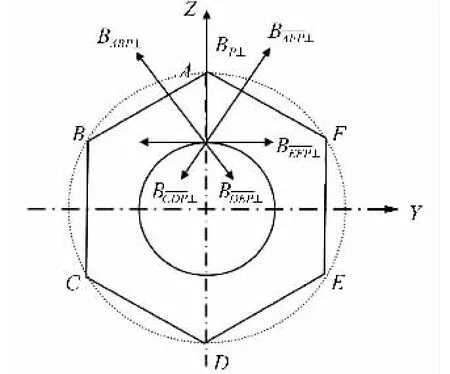
图3 P点磁感应强度的合成示意

综上所述，激磁线圈在点P处产生的径向磁感应强度为

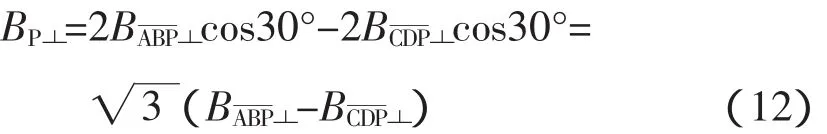
将式（10）、式（11）代入式（12）得出 P点的径向磁感应强度为

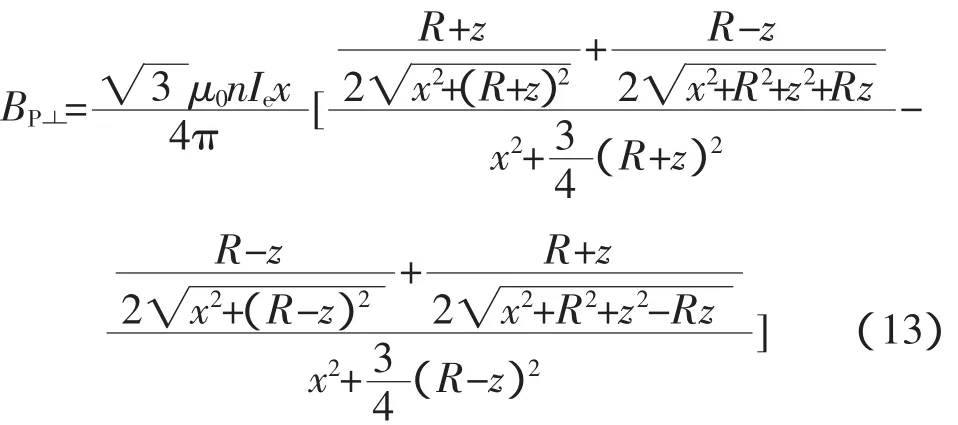
2 计算结果和试验验证

根据式（13），通过改变激磁线圈端面场点P的坐标（x，z），可求得不同位置处的磁感应强度。试验条件下P点初始坐标为（0.02，0.01），激磁线圈的匝数n=510匝，中心半径R=30 mm，当激磁电流Ie变化时，P点沿z轴和x轴方向的径向磁感应强度的值如表1、表2所示，分布曲线如图4、图5所示。

表1 BP┴沿z轴方向的理论计算值 ×10-2T

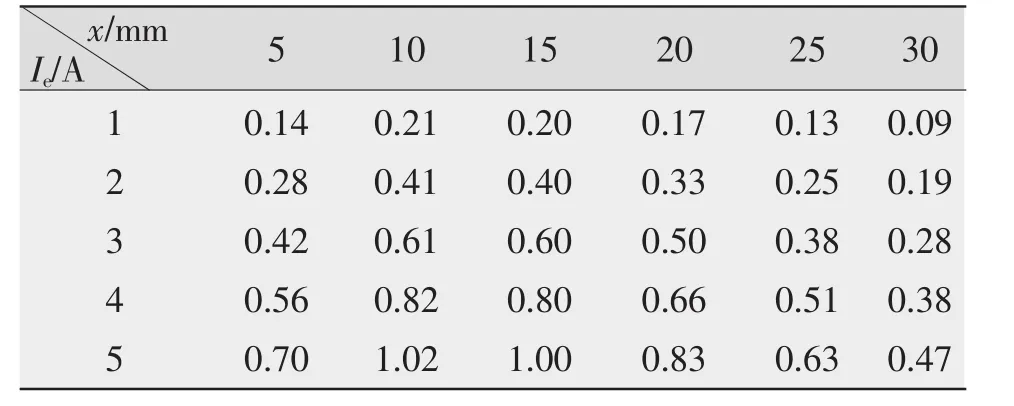
表2 BP┴沿x轴方向的理论计算值 ×10-2T

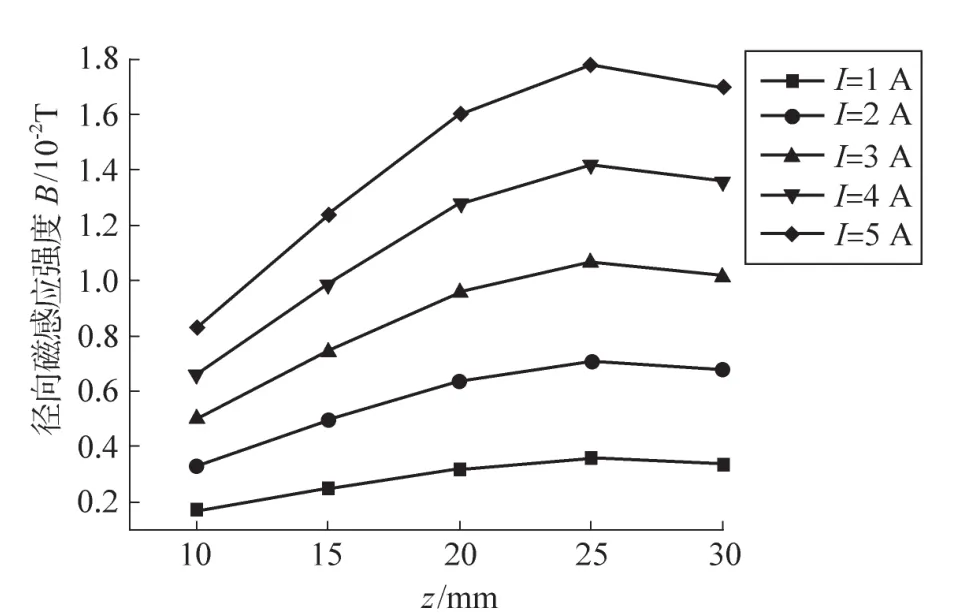
图4 径向磁感应强度沿z轴方向的分布曲线

由图4、图5可得，激磁线圈径向磁感应强度与激磁电流成正比，且电流越大，径向磁感应强度沿x轴和z轴方向变化的斜率越大。此外由图4可知，随着P点与线圈的中心距离z的增大，径向磁感应强度增大，在25 mm处达到最大值，随后有减小的趋势；由图5径向磁感应强度沿x轴的分布可见，随着水平距离x的增加，径向磁感应强度近似抛物线分布，在水平距离为10 mm处达到最大值。

式（13）对同类激磁线圈具有普适性，只要改变参数n、I和R，便可得出激磁线圈径向磁场在径向和轴向上的分布。

由于霍尔效应磁强计结构简单、使用方便，能够实现磁场空间分布状况的测量，采用自制霍尔效应磁强计测量了激磁电流为2 A时激磁线圈端面沿着z轴方向的磁感应强度，具体数据如表3所示。表中同时给出径向磁感应强度的计算值并与之比较。

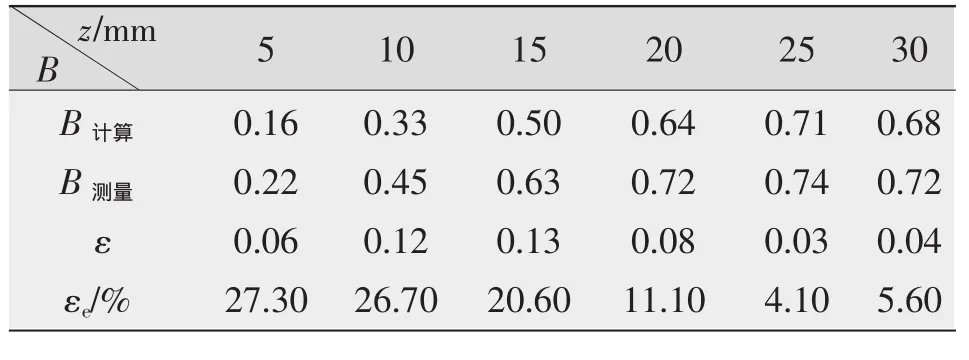
表3 BP┴沿z轴方向的理论计算值 ×10-2T

由表3可见，磁场的测量值大于理论计算值，且两者的相对误差随着z的增大而减小，在25 mm处取得最小值，随后有增大的趋势。原因如下：

（1）霍尔效应磁强计的探头放于被测线圈端面，使霍尔元件的表面与磁力线垂直测得径向磁感应强度，测量值为一定面积内的径向磁感应强度，而理论计算值为一个点的径向磁感应强度，故测量值大于计算值。

（2）径向磁感应强度随着z的增加而增加，在25 mm处达到最大值。在绝对误差相差不大的情况下，相对误差的大小会随着测量值的增大而减小，因此在25 mm处的相对误差最小。

（3）测量装置的误差。由于测量装置中霍尔元件的给定电压的波动、所处温度场的变化以及放大、补偿电路的干扰等都会引起输出结果的波动。

虽然径向磁场的测量值与计算值存在一定差异，但两者的变化趋势和空间分布相似，说明本研究所用简化计算方法适于计算激磁线圈的径向磁场空间分布，可用于磁控旋弧对焊激磁线圈的设计。

3 结论

（1）采用等效线匝的方法建立了管板对焊激磁绕圈的计算模型，根据毕奥-萨伐尔定律，采用简化算法推导了激磁线圈沿管件端面的径向磁感应强度大小的计算公式，该公式也适用于其他激磁线圈。

（2）计算了匝数为510、半径为30 mm的激磁线圈径向磁场沿z轴和x轴方向的径向磁感应强度，结果表明：径向磁感应强度与激磁电流成正比；随z轴方向距离的增加而增大，在25 mm处达到最大值；沿x轴方向近似抛物线分布，在10 mm处达到最大值。

（3）对比了激磁电流为2 A时激磁线圈径向磁感应强度理论计算值和测量值，结果表明：径向磁场的测量值与计算值虽然存在一定差异，但两者趋势一致，能够反映磁场的分布状况。

：

[1]Mori，Yasuda.Magnetically Impelled Arc Butt Welding of Aluminum Pipes[J].Transactions of Japan Welding Society，1990，21（1）：3-10.

[2]许瑞林，杨大佩.磁控旋转电弧对接焊[J].电焊机，1980，（3）：1-7.

[3]易敬曾.磁场计算与磁路设计[M].四川：成都电讯工程学院出版社，1987：1-15.

[4]朱修强.磁控旋转电弧管-板对焊装置及工艺优化研究[D].南京：河海大学，2010.

[5]朱仲良.旋转电弧焊机环形激磁线圈径向磁场的分析计算[J].焊接，1989（1）：10-14.