卫星通信信号调制识别技术研究

李 成，饶志宏

(中国电子科技集团公司第三十研究所，四川成都610041)

0 引言

近年来，随着现代卫星通信技术的高速发展，通信系统中的调制方式趋于多样化和复杂化。在通信对抗领域中，利用调制方式识别技术分析截获的敌方通信信号，确定所截获信号采用的调制方式及相应的物理层参数，然后选择正确的解调参数，再经过一系列后续解扰、解码、解密等工作，就可获得有用的情报信息［1］。

文中针对几种常用MPSK与高阶调制信号，提出了一种基于高阶累积量［2］和谱线特征的识别算法，其思路为:利用高阶累积量完成信号的类间识别，然后利用频谱特征完成QPSK与OQPSK信号的类内识别。最后通过仿真实验验证了该算法具有良好的性能。

1 信号模型

假设MPSK调制信号经过加性高斯白噪声(AWGN)的信道后，且已实现载波恢复和时钟同步，经过下变频，匹配滤波器输出的复基带序列表达式为:

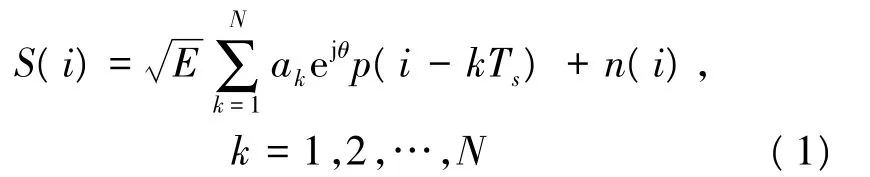
式中，E为信号的平均能量，ak为经过平均功率归一化后的信号码元序列，Ts为码元持续时间，θ为初始相位偏差，p(i)为发送的脉冲波形，n(i)为均值为

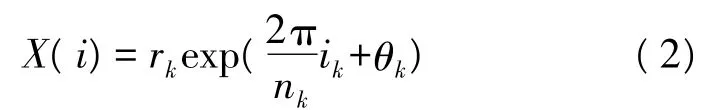
这里k为星座图中的圆周数，16APSK的点形成2个同心圆，故k取值为1或2;nk和rk分别为第k个圆周上的信号点数和圆周半径，一般地，n1=4，n2=12;ik为第 k个圆周上其中一个点，ik=0，1，2，…，nk－1;θk为第 k个圆周上信号点的初始相位。也可以定义相对相位偏移φk和相对半径ρk，这里φk=θk－θ1，ρk=rk/r1，特别的情况 φ1=0，ρ1=0，这样16APSK的星座图也可以通过相对半径和相对相位来描述。零、方差为N0的复高斯白噪声序列，N为仿真的数据长度。将QPSK的正交分量延迟半个码元宽度，就可得到OQPSK的信号。

16APSK［3］星座每个点都有半径和相位，且值都为复数，其信号集如下:

2 基于高阶累积量的分类识别

2．1 数字基带信号各阶累积量的理论值

这里为了消除信号幅度对计算结果的影响，首先可结合信号的星座图来完成对信号的平均功率归一化，。对于MPSK调制信号的星座图，令信号点所在圆的半径为r，那么r与信号功率的关系如下:

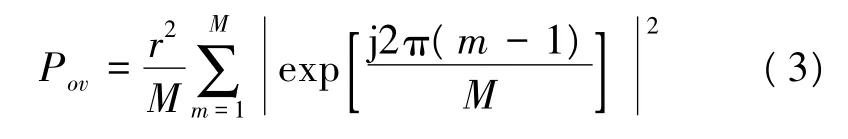
令Pov=1，可得 r=1。

对于16APSK，信号的平均功率可表示为:

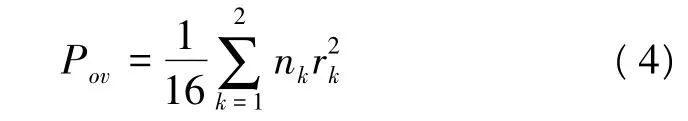
由第1节可知n1为4，n2为12，令 Pov=1，将相对半径 ρk=rk/r1带入上式，可得 ρk约为2．7。

设一个具有零均值的复随机过程X(n)，其p阶混合矩定义为:

因为噪声与信号相互独立，根据高阶累积量的性质，高斯噪声的四阶及以上累积量为零，所以可以忽略高斯白噪声的影响。因此高阶累积量有较强的抑制噪声能力。

对于MPSK信号，式(1)中的码元序列为:

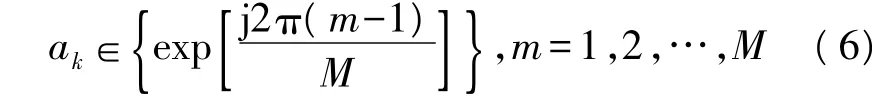
假设发送的码元与和叠加的高斯噪声是独立分布且等概的，对于BPSK信号有:

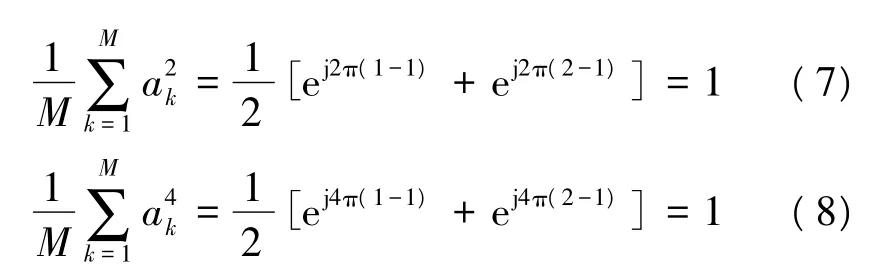
则相应的各阶累积量为:

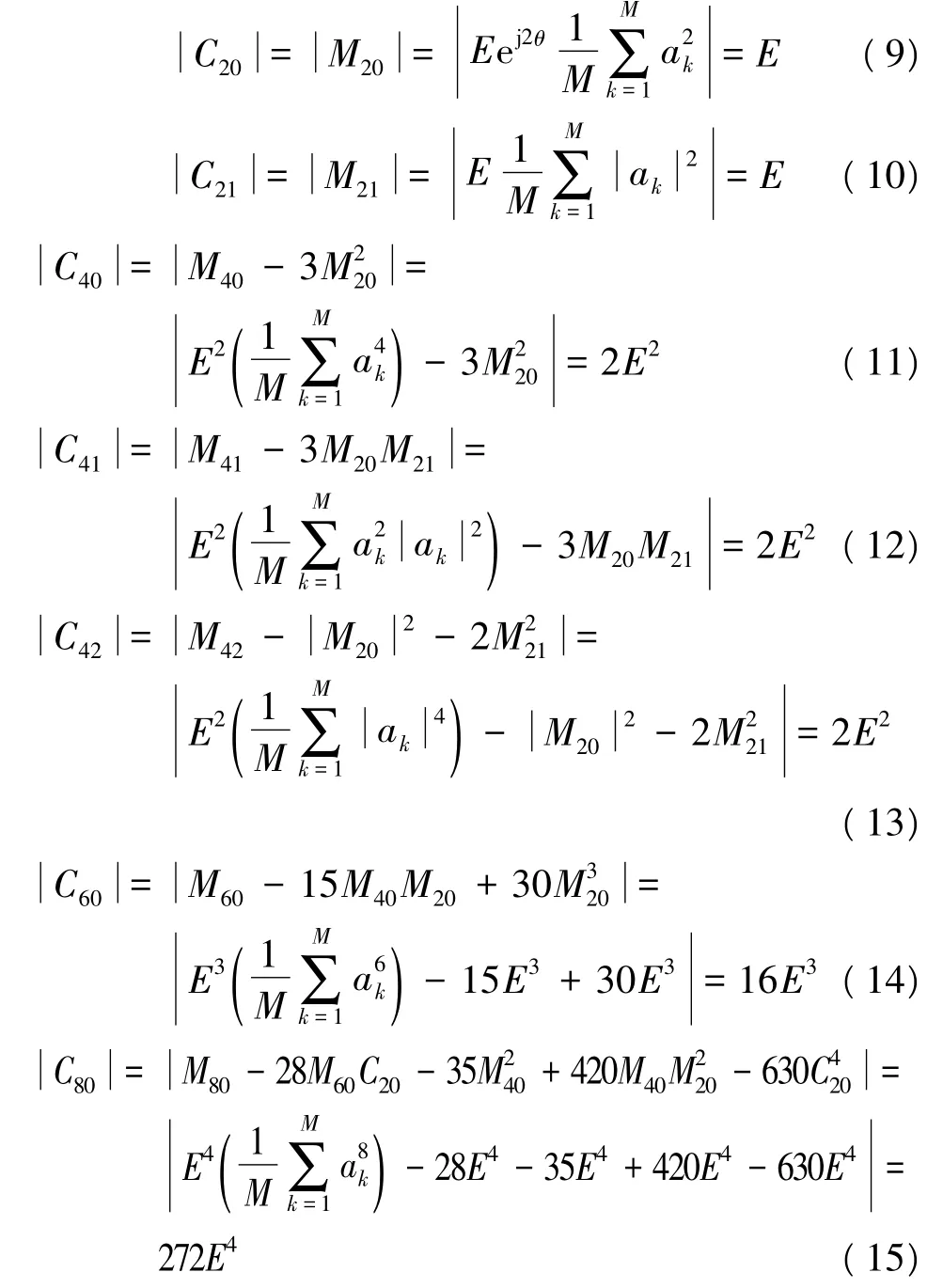
同理可推出QPSK、OQPSK以及8PSK信号各阶累积量的理论值。对于16APSK信号，将星座图内圆半径设为1，相对半径 ρk取值2．7，将式(2)带入式(5)，同样可求得其各阶累积量的理论值。具体的理论值见表1。

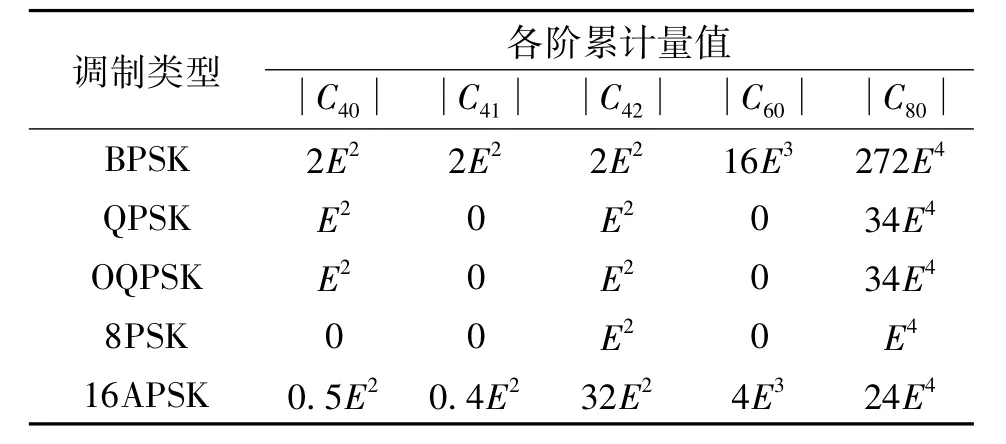
表1 不同调制方式的各阶累计量值Table 1 Value of each order cumulants of different modulation

2．2 特征提取与分类识别

从表1中可以看出，不同调制方式的各高阶累积量不完全相同，因此我们可以从中寻找一些规律，提取信号的特征参量。定义分类特征参数F:

根据高阶累积量的性质可知:

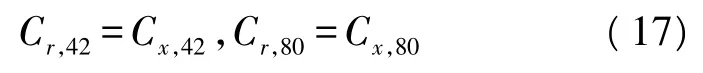
通过以上的推导及我们对特征参量的定义，各调制方式的分类特征参数F有取值如下:

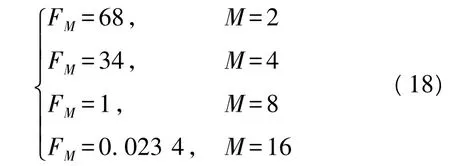
式中，M=2，4，8，16 分别表示 BPSK，{QPSK、OQPSK}，8PSK、16APSK 调制。对于 16APSK，在计算F值时，由于相对半径在取不同值时对结果影响不大，所以我们只考虑ρk=2．7。由定义可知，F为信号八阶累积量的模与四阶累积量模的平方的比值，故接收信号的固定载波相位误差θ对F的值没有影响。

根据式(18)，我们得到不同调制方式特征参数F的理论值。但是在有噪声干扰的环境下，特征参数F的值会有偏差，故文中做了不同调制方式在特定信噪比条件下，其特征参数的统计分布仿真实验，见图1。

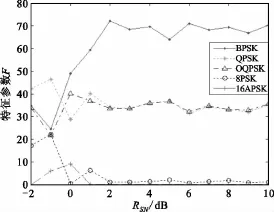
图1 不同调制方式的特征参数统计分布Fig．1 Statistical distribution of the characteristic parameter of different modulation types

从图1中可以看出，在信噪比SNR＜1 dB时，不同调制方式的特征参数曲线分布有交叉，基本无法有效识别。在SNR≥2 dB时可以看出，BPSK的特征参数F值范围在63～72之间;QPSK与OQPSK的F值曲线基本重合，范围在29～37之间;8PSK的F值范围大致在0．8～3．5之间;而16APSK的F值范围大致在0．005～0．3之间。因此可以在上述各区间范围之外找出没有任意区间覆盖到的合适的值，并将其作为判决门限，故有th1=40，th2=5，th3=0．5，则判决准则为:

F＞th1，调制类型判为BPSK;

th2＜F＜th1，调制类型判为{QPSK、OQPSK};

th3＜F＜th2，调制类型判为8PSK;

F＜th3，调制类型判为16APSK。

3 基于谱线特征的分类识别

从2．2节可以看出，QPSK和OQPSK信号的各阶累积量完全相同，而它们的星座图也完全相同，如果直接对信号进行高阶累积量计算，则用传统的求高阶累积量方法无法对它们进行识别分类。由于OQPSK信号是两路码元时延后的QPSK信号，两路码元相差半个码元周期，所以我们可以通过寻求其谱线特征［4－5］完成类内识别。

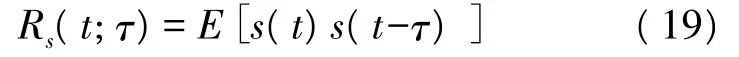
假设调制信号s(t)的时变共轭自相关函数为:若Rs(t;τ)具有周期T0，则称s(t)为二阶循环平稳过程。不难看出，Rs(t;τ)取τ=0即为信号二次方形式的统计期望值，其傅里叶变换形式即为信号的平方谱:

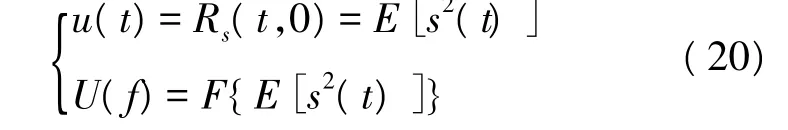
我们知道，一个信号的时变共轭自相关函数的周期性使得该信号在频率域上能够产生出离散谱线，故可通过求时变共轭自相关函数来得到其频谱。所以u(t)的周期特性使U(f)具有离散谱线的特征。

同样地，如果s(t)是四阶循环平稳的，其四次方统计期望值可以看作是四阶时变共轭相关函数R4s(t，τ)取τ=0的特例，相应的傅里叶变换形式即为四次方谱:

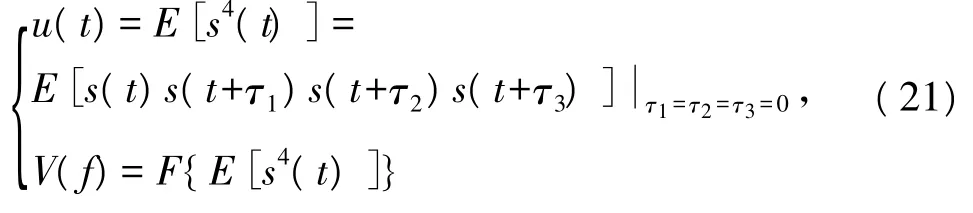
下文将针对QPSK与OQPSK信号，通过分析其平方谱与四次方谱［6］的谱线特征来进行分类识别。

3．1 QPSK信号的平方谱与四次方谱

由1．1节可知 QPSK信号的时域波形可以表示为:

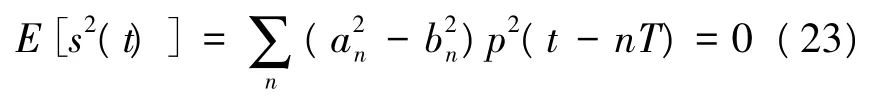
根据前面的分析，QPSK信号的平方谱不存在离散谱线，其或为载波分量，或为码速率分量。QPSK信号四次方形式的统计期望是以T为周期的函数，其四次方谱可表示如下:

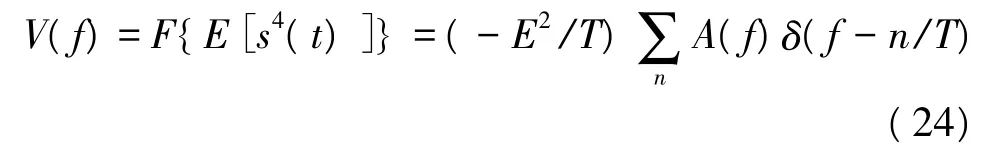
式中，A(f)=F{p4(t)}，p(t)一般采用升余弦型脉冲，表示成形脉冲;平方根升余弦滤波器滚降系数α通常取0＜α＜0．5。因为V(f)的非零区间为［－(1+α)/2T，(1+α)/2T］，所以 n∈{0，±1，±2}，故根据 δ(t)函数的性质可知，V(f)只在频率为{0，±1/T，±2/T}处出现离散谱线。由于幅度A(f)随频率衰减速度至少为f－4，所以f=±2/T处表示码速率分量的谱线幅度远远小于{0，±1/T}处表示载波分量的谱线。

3．2 OQPSK信号的平方谱与四次方谱

将QPSK信号的正交分量延迟半个码元宽度，就得到OQPSK信号，其表达式如下:

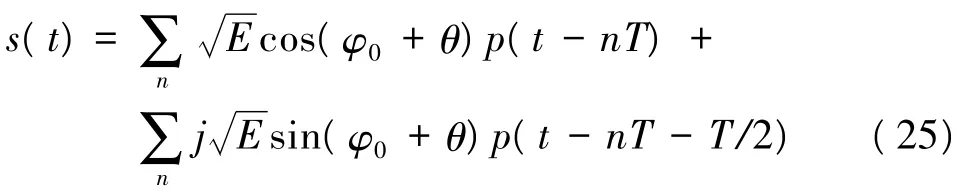
式(25)中s(t)二次方形式的统计期望是周期为T的函数，平方谱E［U(f)］在f=±1/T处存在表示码速率信息的离散谱线:

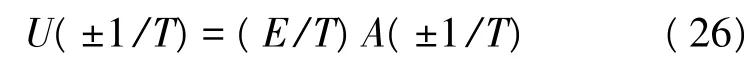
式中，A(f)=P(f)·P(f)。

OQPSK的四次方谱V(f)在频率{0，±2/T}处出现离散谱线，即:

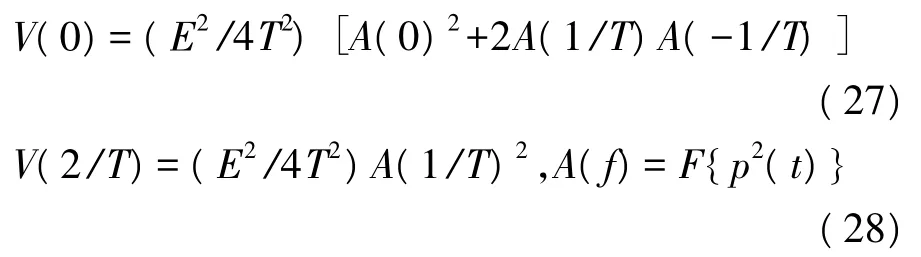
实际上OQPSK信号的谱线幅度随频率衰减较快，频率f=±2/T处的谱线很难被检测到，故在下面的仿真实验当中选取的信号能量较大。

因此可以通过平方谱与四次方谱将QPSK与OQPSK信号区分开来。

4 实验仿真及结果

根据上面的分析，在以下试验中我们分别仿真了基于高阶累积量的识别算法性能，以及基于谱线特征的QPSK、OQPSK类内识别。

仿真实验一:选取仿真信号长度为8 192×80，载 频 fc=4．4 MHz，码 速 率 R=216 kb/s，采 样率25 MHz，不同调制方式在特定信噪比下的特征参数值如图1所示。

可以看出，在 RSN≥2 dB时，除了 QPSK与OQPSK的曲线基本重合外，各调制方式的特征参数F值曲线区别很明显，故可以很好地将 BPSK、{QPSK、OQPSK}、8PSK、16APSK 信号区分开。图 2为基于高阶累积量的类间识别性能图。

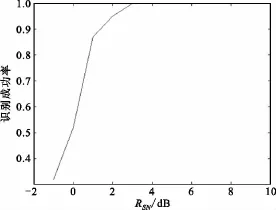
图2 基于高阶累积量的识别算法性能曲线Fig．2 Performance curve of the recognition algorithm based on higher order cumulants

可以看出，文中提出的算法在信噪比RSN＞3 dB时正确识别率就已达到95%以上，因此文中算法也适用于低信噪比下MPSK信号的识别。

仿真实验二:分别对OPSK与OQPSK信号进行了二倍频和四倍频的仿真，同样地，选取与实验一参数相同的信号。QPSK信号的二倍频、四倍频，OQPSK信号的二倍频、四倍频的仿真实验图分别如图3、图4、图5和图6所示。

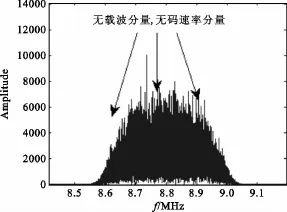
图3 QPSK信号的二倍频Fig．3 Square spectrum of the QPSK signal

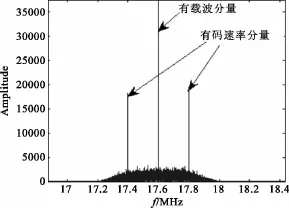
图4 QPSK信号的四倍频Fig．4 Quartic spectrum of the QPSK signal

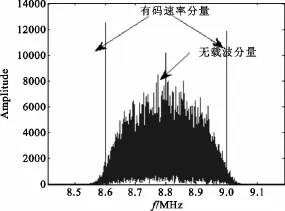
图5 OQPSK信号的二倍频Fig．5 Square spectrum of the OQPSK signal

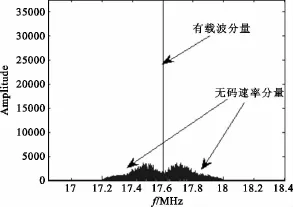
图6 OQPSK信号的四倍频Fig．6 Quartic spectrum of the OQPSK signal

可以看出，QPSK信号的二次方谱线与四次方谱线同OQPSK信号相比都有很大不同。二倍频无载波分量和码元分量，四倍频出现载波分量和码元分量时判为QPSK;二倍频无载波分量、但有码元分量，四倍频出现载波分量，但无码元分量时判为OQPSK。

5 结语

针对几种常见的MPSK及高阶调制16APSK卫星通信信号，文中提出的识别方法为:利用高阶累积量来完成不同点数信号的类间识别，然后利用二次方谱与四次方谱完成同点数QPSK、OQPSK信号的类内识别。理论分析与仿真验证表明以上识别算法有良好的性能。

［1］ 粟欣，许希斌．软件无线电原理与技术［M］．北京:人民邮电出版社，2010．SU Xin，XU Xi－bin．Software Radio Principle and Technology［M］．Beijing:The People's Posts and Telecommunication Press，2010．

［2］ SWAMI A，SADLER B M．Hierarchical Digital Modulation Classification Using Cumulants［C］//IEEE Transactions on Communications．America:IEEE，2000:416－429．

［3］ ETSI．EN 302 307 V1．2．1，Second Generation Framing Structure，Channel Coding and Modulation Systems for Broadcasting，Interactive Services，News Gathering and Other Broadband Satellite Applications［S］．Switzerland:Digital Video Broadcasting(DVB)，2009:25－28．

［4］ 李少凯，董斌，刘宁．基于谱线特征的 MPSK调制识别［J］．通信技术，2010，43(08):127－131．LI Shao－kai，DONG Bin，LIU Ning．Modulation Recognition of MPSK Signals based on Spectrum Line Feature．

［5］ DOBRE O A，BDI A A，NESS Y B．Survey of Automatic Modulation Classification Techniques:Classical Approaches and New Trends［C］//IEEE Transactions on Communications．America:IEEE，2007:137－156．

［6］ 杨志俊，范海波．基于谱分析的通信信号调制方式自动识别［J］．无线通信技术，2003，2(08):30－33．YANG Zhi－jun，FAN Hai－bo．Automatic Modulation Recognition of Communication Signal Based on Spectral Aynalysis［J］．Wireless Communications Technology，2003，2(08):30－33．