基于FRFT的复合chirp信号分析*

张小乾，姚远程，秦明伟

(西南科技大学信息工程学院，四川绵阳621010)

0 引言

线性调频(chirp)信号常见于雷达、声纳和移动通信等系统中。chirp信号通过非线性相位调制，具有很大的时宽带宽积，不仅解决了距离分辨力与探测距离之间的矛盾，而且具有好的速度分辨力，因而备受青睐。对比复合chirp信号以及单斜率chirp信号这两种信号的模糊函数图，－3 dB模糊度图，距离模糊函数图以及速度模糊函数图，可发现复合chirp信号相对单斜率chirp信号具有更好的速度分辨力和距离速度联合分辨力［1］。FRFT在90年代中期被引入了信号处理领域，并指出了它的物理意义是给定信号时频分布在时频域内某一与时间轴成“角度轴线上的积分投影”［2－3］。近年来，FRFT 作为信号时频分析的研究工具受到了研究者的广泛关注。此外有些学者也在进行FRFT对chirp信号的检测的研究［4－6］。

文中利用复合chirp类信号在FRFT域的时频能量聚集性，以及分数阶傅立叶变换是一种一维的线性变换，在处理多分量信号时可避免交叉项的困扰。采用在FRFT域逐次滤波法实现对复合chirp信号的检测与估计。

1 FRFT与WVD

1．1 FRFT 的定义

FRFT是一种新型的信号时频分析的有力工具，是传统傅立叶变换更广义的形式，若将传统傅立叶变换的算子看作从时间轴逆时针旋转π/2到频率轴，则分数阶傅立叶变换的变换算子就是可旋转任意角度α=p×π/2的算子。信号x(t)的角度为α的分数阶傅立叶变换的定义为［7－8］:

式中，下标表示角度为α的连续FRFT，其变换核为:

式中，Bα=α为旋转角度，用时频平面旋转的观点来解释，则有以下等式成立:

1．2 平滑伪Wigner－Ville分布的定义(SPWVD)

信号x(t)的SPWVD定义为

2 复合chirp信号的时频分析方法

2．1 复合chirp信号简介

复合线性调频信号是采用正负两个斜率分量的线性调频信号，调频斜率k满足其中 tp为信号脉宽，B为信号的带宽。其角频率随时间的函数关系如下:

由式(4)可以看出，该信号的时宽带宽积是单斜率chirp信号的两倍，具有比单斜率chirp信号更大的时宽带宽积，因此具有更好的脉冲压缩性能［1］。该信号的包络形式可表达式为:

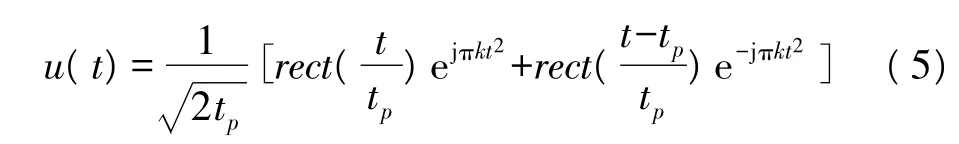
式中，

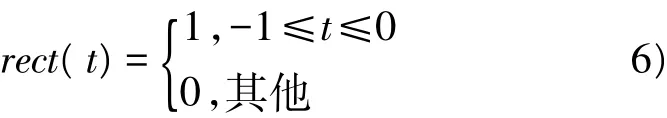
2．2 复合chirp信号的时频分析方法

含有噪声的单分量chirp信号可表示为

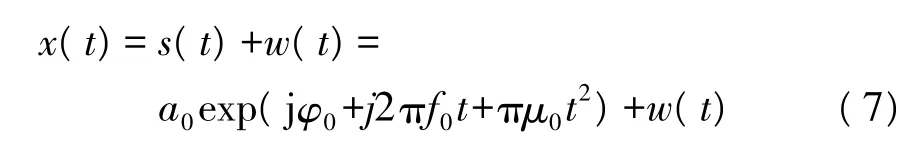
式中有－Δt/2≤t≤Δt/2，Δt为信号的周期，a0，φ0，f0，μ0为未知参数，信号 s(t)的幅度为 A，w(t)为加性高斯白噪声，则上述chirp信号检测和估计过程可描述为

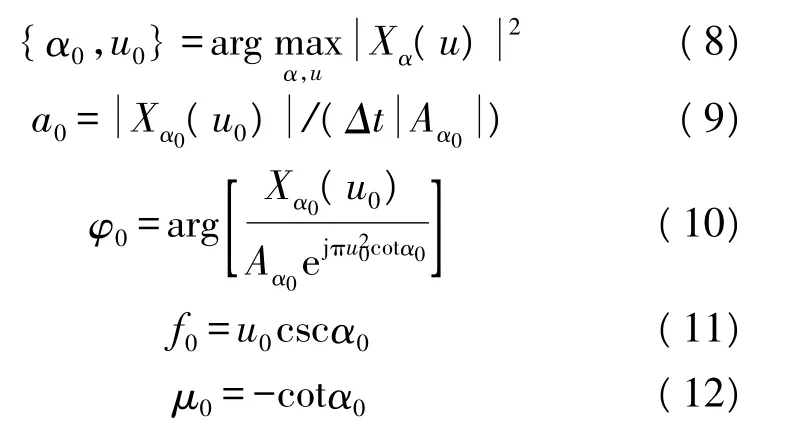
FRFT可以看成是复合chirp信号的分解得到的，FRFT的变换核实质是一组chirp信号(FRFT的分解基)，当需要处理的复合chirp信号与某组基的调频率吻合时，该信号就必然在改组基中的某个基上形成一个δ函数，而在别的基上为零。由此得出chirp类信号在FRFT域具有很好的时频聚集性。复合chirp信号从单个码元来看，就是chirp信号，只不过从总体来看是多分量的复合chirp信号而已。所以，在对该信号进行p从0～4阶的FRFT变换时，只有在与自身线性调频分量相吻合的阶次，才会形成能量的聚集。因此可通过这种方式，来逐一得到信号各分量的调频斜率和载波。为了防止强分量掩盖若分量的可能，可以在分数阶域逐次滤波来一一检测［8］。

由分解型FRFT的原理可知，若信号x(t)的最高频率分量为F，则Xp(u)可由下式计算

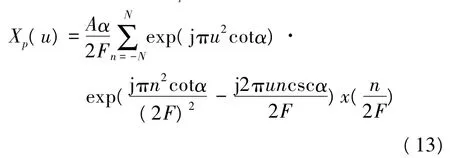
将变量u离散化后得

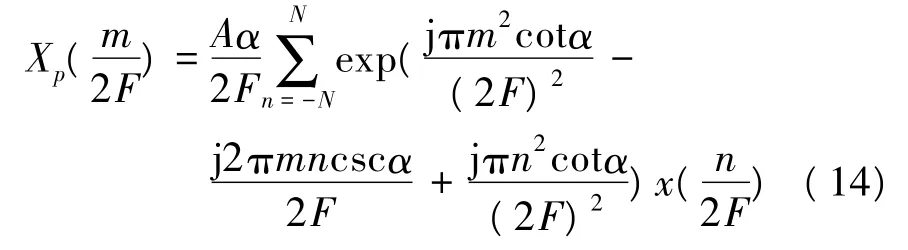
分析过程中采用两级搜索的方法，这样可以在保证估计精度的同时降低计算的复杂度。首先，以式(14)为计算工具，对变量p和u采用大的搜索步长(分辨率较低)进行直接搜索，得到p0及u0的粗略估计;然后，把上一步的结果作为初始值，在式(13)的基础上，利用牛顿法进行迭代搜索，得到参数的精确估计，其迭代过程可表示为

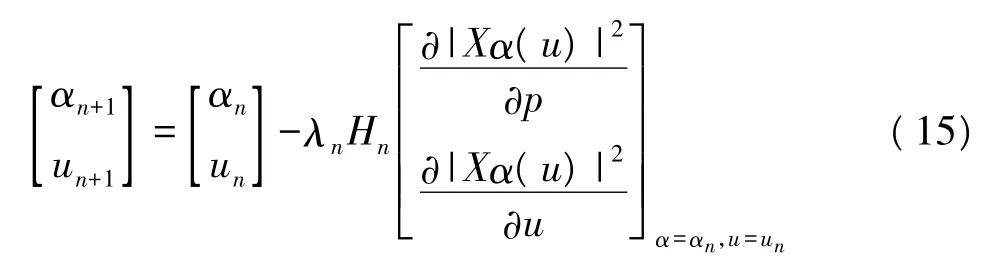
式中，αn+1及un+1为参数的第n次搜索的结果，λn为第n次搜索的步长系数，Hn为函数在(αn，un)的尺度矩阵，可通过迭代的方法求得。

3 仿真

3．1 利用FRFT方法的仿真

为了验证思路的正确性，选用复合chirp雷达信号的旋转角度α=6°(取逆时针旋转为正)，时间长度为t0=0．995 0 μs， N =1 000， fs=1．005 GHz， f0=－0．1 GHz， k01=0．977 6 GHz/μs， k02=－0．640 8 GHz/μs，加入均值为 0，标准偏差为 0．5的高斯白噪声仿真。在进行FRFT之前，对信号进行量纲归一化处理，归一化尺度因子

归一化宽度为

归一化区间为

采样点数

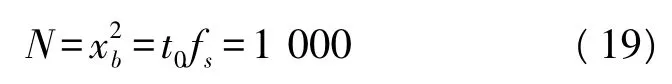
图1是对复合chirp信号进行1到3阶次的FRFT后的幅度谱。因为复合chirp信号本身含有4个线性调频分量，所以如图1所示，信号在该变换域中形成4个冲击。

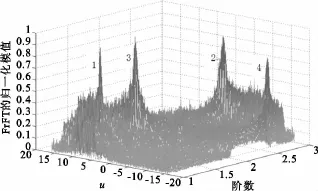
图1 复合chirp信号的分数阶傅里叶谱Fig．1 FRFT spectrum of composite chirp signal

由于4个线性调频分量中的调频斜率是两两相同的，所以这4个冲击分别两两对应在阶次1．5和2．6左右。图1中的分量1和3的峰值截面如图2所示。通过全域搜索发现，冲击聚集在分数阶域的坐标为 u1=－2．51，u3=－12．12，其变换阶次为 p=1．447。

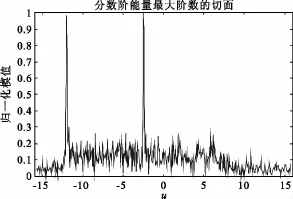
图2 分数阶傅里叶谱峰值的截面(p=1．447)Fig．2 Section of FRFT spectrum's peak(p=1．447)

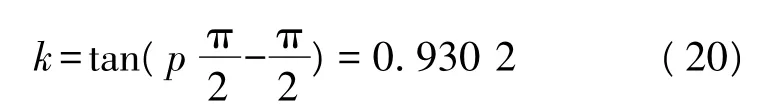
因此分量1和分量3的归一化调频斜率为

所以，分量1和分量3的真实调频斜率为

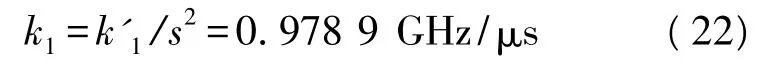
冲击的坐标在分数阶域为u1=－2．51，u3=－12．12。量纲归一化后，分量1和分量3与时间轴的夹角为β'1=arctank'1，由此可以得到上述两个分量的归一化初始频率分别为

分量1和3的实际初始频率分别为

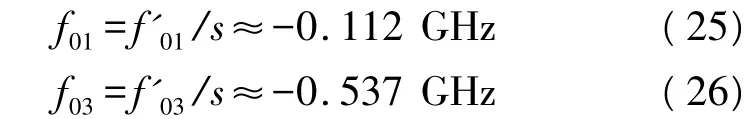
同理可以得出，

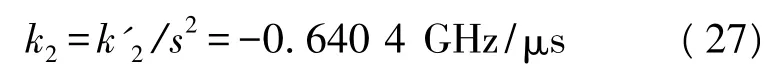
分量2和4的实际初始频率分别为

通过FRFT全域搜索法得到信号的初始频率为f01=－0．112 GHz。两个分量的调频斜率分别为 k1=0．978 9 GHz/μs，k2=－0．640 4 GHz/μs。

由复合chirp信号的调频斜率与旋转角度的关系为k=tan(α－π/2)，且α=pπ/2为FRFT的逆时针旋转角度，因此复合chirp信号的分量1和分量3的调频斜率为

3．2 利用SPWVD方法的仿真

为了验证FRFT方法的有效性，特取上述信号的一个周期做SPWVD时频分析，仿真结果如图3所示。由图计算可知，信号的初始频率为 f01≈－0．08 GHz。两个分量的调频斜率分别为 k1≈0．1 GHz/μs，k2≈－0．7 GHz/μs。

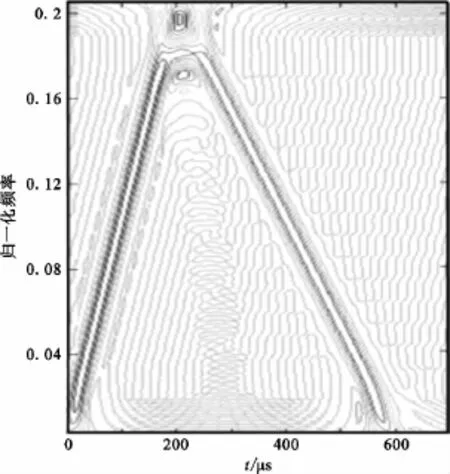
图3 复合chirp信号的SPWVD(α=6°)Fig．3 SPWVD of composite chirp signal(α=6°)

4 结语

FRFT可以看作是信号在时频平面内绕原点旋转任意角度后所构成的FRFT域上的表示，将FRFT分解为信号卷积形式利用FFT计算，具有计算速度快的优点。由于复合chirp信号在FRFT域呈现的冲激特性，当FRFT的阶数与复合chirp信号的调频斜率一致时，信号呈现尖峰，以此实现复合chirp信号的检测。实验仿真结果表明，用分数阶全域搜索法对复合chirp信号的起始频率和调频斜率进行估计，其中起始频率的误差为Δf0=0．012 GHz，调频斜率的误差分别为 Δk01=0．001 3 GHz/μs 和 Δk02=－0．000 4 GHz/μs，可以看出该方法所得结果误差很小，而采用SPWVD分析方法误差较大。所以，采用分数阶全域搜索法对检测多分量复合chirp信号的起始频率和调频斜率是一种非常有效的方法。

［1］ 刘领容，王凌，姚远程，等．复合LFM信号的模糊函数分析［J］．西安理工大学学报，2011，27(04):481－485．LIU Ling－rong，WANG Ling，YAO Yuan－cheng，et al．Analysis of Ambiguity Function of Combined Linear Frequency Modulation Signal［J］．Journal of Xi’an University of Technology，2011，27(4):481－485．

［2］ ALMEIDA L B．The Fractional Fourier Transform and Time－frequency Representations［J］．IEEE Trans．Signal Processing，1994，42(11):3084－3091．

［3］ 卢慧英，朱灿焰．基于 FRFT的多 LFM信号的分离及参数估计［J］．通信技术，2011，44(09):32－35．LU Hui－ying，ZHU Can－yan．Multi－LFM Signal Separation and Parameter Estimation based on FRFT［J］．Communications Technology，2011，44(09):32－35．

［4］ 高凤鹍，贾海涛．基于时频分布的多分量LFM信号检测［J］．通信技术，2010，43(12):1－3．GAO Feng－kun，JIA Hai－tao．Multi－Component LFM Signal Detection based on Quadric Time－Frequency Distribution［J］．通信技术，2010，43(12):1－3．

［5］ 赵宏伟，李勇．一种基于时频分布的跳频信号检测方法的研究［J］．信息安全与通信保密，2006(06):98－99．ZHAO Hong－wei，LI Yong．Research of FH Signal Detection based on Time－Frequency Distribution［J］．China Information Security，2006(06):98－99．

［6］ 李靖，王树勋，汪飞．基于分数阶傅里叶变换的chirp信号时频分析［J］．系统工程与电子技术，2005，27(06):988－990，1015．LI Jing，WANG Shu－xun，WANG Fei．Chirp Signal A-nalysis based on PWD in Fractional Fourier Transform Domain［J］．Systems Engineering and Electronics，2005，27(6):988－990，1015．

［7］ 张峰，陶然．分数阶Fourier域谱估计及其应用［J］．电子学报，2008，36(09):1723－1727．ZHANG Feng，TAO Ran．Power Spectral Estimation and Its Application in Fractional Fourier Domain［J］．ACTA ELECTRONICA SINICA，2008，36(9):1723－1727．

［8］ 陶然，邓兵，王越．分数阶傅里叶变换及其应用［M］．北京:清华大学出版社，2009，98－115．TAO Ran，DENG Bing，WANG Yue．Fractional Fourier Transform and Its Applications［M］．Bing Jing:Tsinghua University Press，2009，98－115．