基于MIMO系统的差分解码算法及性能分析

孙 刚，魏东兴，王 伟

(1．大连理工大学信息与通信工程学院，辽宁大连1106024;2．中国人民解放军66440部队，河北石家庄050081)

0 引言

近年来，由于多入多出(MIMO，Multiple Input Multiple Output)技术可以显著提高无线通信系统的频带利用率［1］，因而得到了广泛研究。很多学者已经提出了各种各样的空时编解码方案［2-7］。但是大多数方案都假设系统接收端已知信道状态信息(CSI，Channel State Information)。当信道变化缓慢时，可以通过周期性发送训练序列来实现信道估计，但会损失一定的带宽［8］，降低频带利用率;而且当天线数目较多［8］或者信道变化较快时，接收端很难获得准确的CSI。另外，在帧长比较大的情况下，准静态的假设也会变得不合理。所以，有些情况下，依赖信道估计并不是最优方案，有必要研究不需要做信道估计的非相干解码技术。

文献［9］提出了一种单用户两发送天线的差分编解码方案，收发双方都不需要CSI。文献［10］在文献［9］的基础上讨论了发送天线超过两个的情况，并较好地改善了解码性能。文献［11］提出了一种基于维特比算法的改进差分空时编解码方案。理论上来说，这些方案适用于任意数目的发送天线和接收天线，也可以使用任意的调制方式，但是解码复杂度会随着天线数的增加变得无法接受。以上都属于单用户差分编解码方案，多用户MIMO系统的相干编解码方案也已经有了较多的研究。文献［12］研究了如何消除多用户MIMO系统的用户间干扰，文献［13］研究了基于准静态正交空时分组码(QOSTBC，Quasi Orthogonal Space Time Block Code)的多用户编解码方案。文献［14］提出了一种针对两用户SISO(Single Input Single Output)系统的差分编解码方案，文献［15］将该差分编解码方案推广到了两用户的MIMO系统，提出了部分差分解码算法和exact解码算法。其中部分差分解码算法对两个用户连续发送的两个分组进行最大似然联合解码，再将结果对其中一个用户的CSI矩阵求极大值。该方法理论上很合理，但是CSI矩阵是由自然条件决定的，理论上求取的极大值点跟实际的CSI矩阵有可能不一致。exact算法则有着比较高的解码复杂度。

针对上述问题，首先提出了一种基于正交空时分组码(OSTBC，Orthogonal Space Time Block Code)的部分差分解码方案，只需要知道一个用户的CSI即可实现解码，解决了文献［15］中部分差分解码算法理论值和实际值不一定相符的问题。然后又给出了一种低复杂度的完全差分解码算法，不需要知道任何一个用户的CSI即可完成解码，同时针对该算法进行了预编码优化，并通过仿真给出了最优旋转角度。最后，对完全差分解码算法进行了针对复数加法和乘法的复杂度分析。仿真证明，提出的完全差分解码算法在保证一定解码性能的前提下有效降低了解码复杂度。

1 系统模型

系统发送端有两个用户，每个用户配备NT根发送天线。接收端有一个用户，配备NR根接收天线，假设信道为准静态平坦瑞利衰落信道，每个发送分组包含的符号个数为K。

在第k个分组时，发送端到接收端的信号关系可以表示为

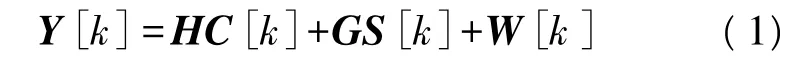
式中，Y［k］为 NR×NT阶的接收信号矩阵。C［k］和S［k］分别是用户1和用户2的发送符号矩阵，均为NT×NT阶矩阵。H和G分别是用户1和用户2的信道衰落矩阵，均为NR×NT阶矩阵，其元素均为服从均值为0，方差为1的独立同分布复高斯随机变量，其中H的第i行，第j列元素为用户1的第j根发送天线到第i根接收天线之间的信道衰落因子。W［k］为NR×NT阶的加性高斯白噪声矩阵，其元素均为服从均值为0，方差为1/2的独立同分布复高斯随机变量。假定两个用户在第k个分组发出的符号同时到达接收机并且信号的传输得到了合适的同步。两个用户的信号都处于相同的频段，并且都没有使用任何正交手段来区分信号。

2 基于OSTBC的差分编解码算法

2．1 基于OSTBC的差分编码

发送端每个用户的差分编码流程都是一样的，具体以用户1为例，按照图1的差分编码流程，每个分组发送的比特数为K×b，其中b为星座图中每个码元传输的比特数。用户1将K×b个比特调制成K个符号，然后进行正交空时编码，得到方阵P［k］。该方阵与前一个发送矩阵通过差分编码得到新的发送矩阵。假设第k-1个分组的发送矩阵为C［k-1］，则有

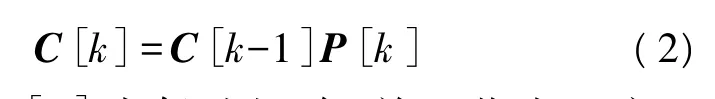
式中，k≥1，C［0］为任选矩阵，并且收发双方已知C［0］的值。

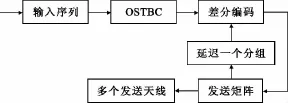
图1 单个用户的差分编码流程Fig．1 Differential encoder of single user

2．2 基于OSTBC的部分差分解码算法

信道在连续两个发送分组间的变化是可以忽略的，用户1和用户2的输入序列生成的正交空时分组码矩阵分别设为 P［k］和 Q［k］，P［k］和 Q［k］经过差分编码之后生成的发送矩阵分别设为C［k］和S［k］。根据式(1)，在第k和k-1个分组分别有

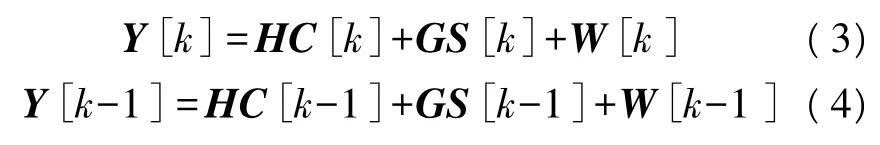
式中，k≥1，C［0］，S［0］为任选矩阵，并且收发双方都已知 C［0］和 S［0］。

利用式(3)和式(4)消掉H并代入式(2)，可以得到这两个分组的收发信号关系为

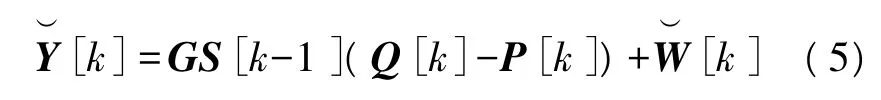
式中，

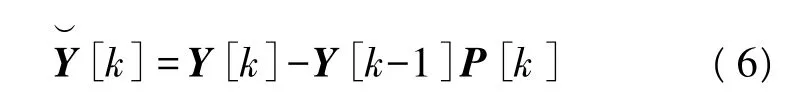
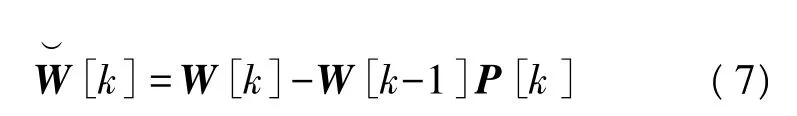
可以看出，式(6)、式(7)中的噪声不再是高斯分布，而是依赖于 W［k］、W［k-1］和 P［k］。接下来的运算忽略已发信号对噪声的影响，仍然假定噪声是高斯分布。解码性能会有一定的损失，但在差分编解码方案中这种假定是可行的［16］。

文献［15］证明了在两个用户情况下，仅仅根据连续两个发送分组进行差分解码不可能得到发送序列。但是利用两个分组可以采用基于最大似然准则的部分差分解码方案，对第k和k-1连续两个分组，进行最大似然联合解码。对任意的k≥1，根据最大似然准则判决为

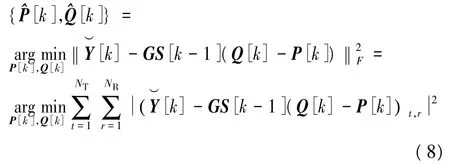
式中，t表示分组的时隙，r=1，2，…，NR，表示接收天线，‖·‖F表示矩阵范数。

由于利用最大比合并规则［2］可以很容易将接收天线数从1推广到大于等于2的情况，所以为了简便起见，对任意的k≥1，只考虑接收天线数为1的时候，最大似然准则判决变为

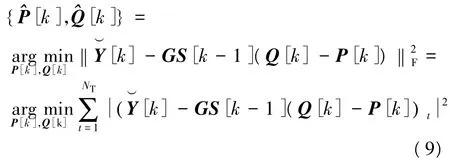
此时，只需要用户2的CSI即可对两个用户的发送序列进行解码。如果小区内有一个用户因为信号弱等原因无法估计信道，那么只需要通过发送训练序列估计出该小区内另外一个信号较强的用户的CSI即可对这两个用户进行最大似然联合解码。

当 k=1时，利用已知的 C［0］和 S［0］，通过最大似然判决准则可以得到两个用户的发送序列Q［1］和 P［1］;当 k=2 时，利用已知的 C［0］、S［0］、Q［1］和 P［1］可以得到发送序列 Q［2］和 P［2］。以此类推可以对其他分组依次进行解码。这种解码算法对任意阶数的发送矩阵都可以使用，并且通过最大比合并准则可以很容易推广到多个天线。

2．3 低复杂度的完全差分解码算法

信道在连续三个发送分组间的变化是可以忽略的。用户1和用户2都有两个发射天线，也即NT=2，用户1和用户2的输入序列生成的OSTBC矩阵P［k］和 Q［k］使用 Alamouti编码矩阵［2］，故 C［k］和S［k］也是Alamouti矩阵。为简明起见，接收端仅设一个接收天线，即NR=1。

根据 Alamouti矩阵规则，C［k］和 S［k］矩阵分别为

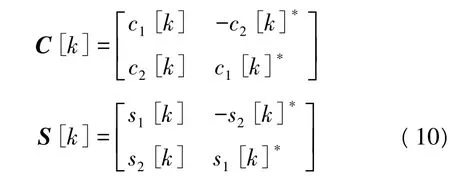
式中，(·)*表示共轭运算。

根据式(1)，对于接收天线有

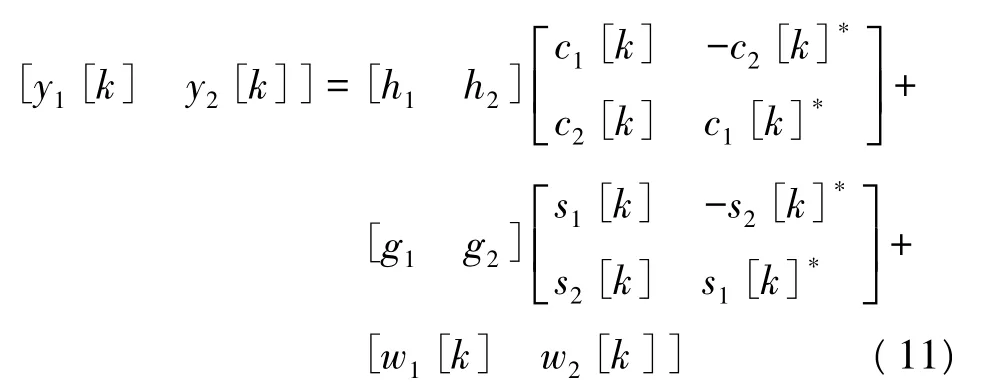
式中，［y1［k］ y2［k］］表示接收天线在时隙 1 和时隙2接收到的两个信号，［h1h2］表示用户1的天线1和天线2到接收天线之间的信道增益系数，［g1g2］表示用户2的天线1和天线2到接收天线之间的信道增益系数。

将接收信号矩阵和信道矩阵改写成正交矩阵，式(11)可以重新写成如下矩阵形式:

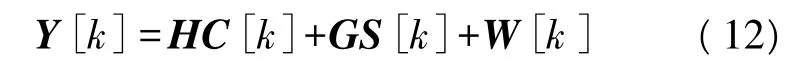
式中，

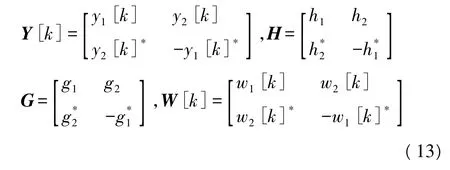
根据式(5)，对任意的k≥2，可以得到如下关系:

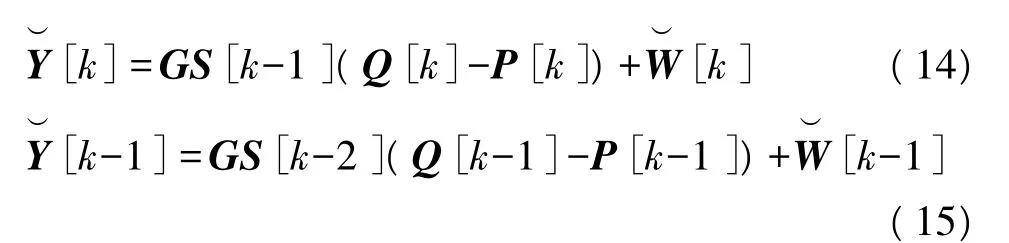
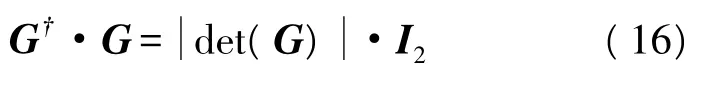
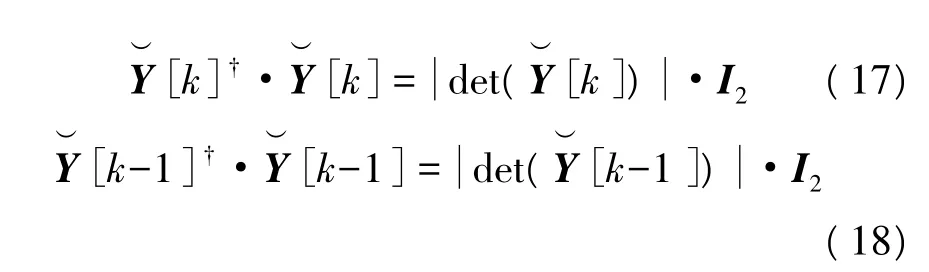
式中，(·)†表示共轭转置运算。

令X［k］=S［k-1］(Q［k］-P［k］)，在式(14)两侧分别左乘和右乘和右乘在式(15)两侧分别左乘将得到的两个等式相减可以得到

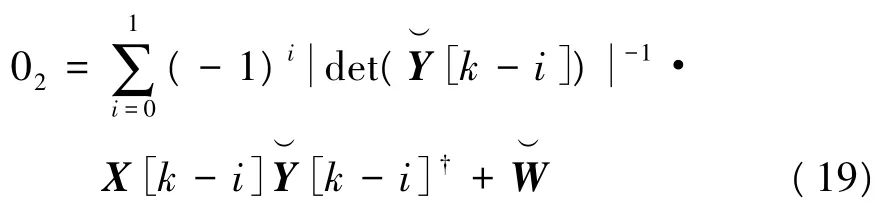
式中，

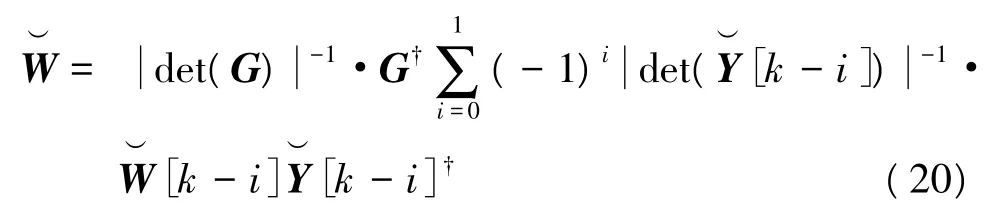
可以看出，式(19)、式(20)中的噪声不再是高斯分布，而是依赖于接收信号和CSI。但是接下来的运算中会忽略这些信号对噪声的影响，仍然假定噪声是高斯分布。

根据最大似然准则判决为

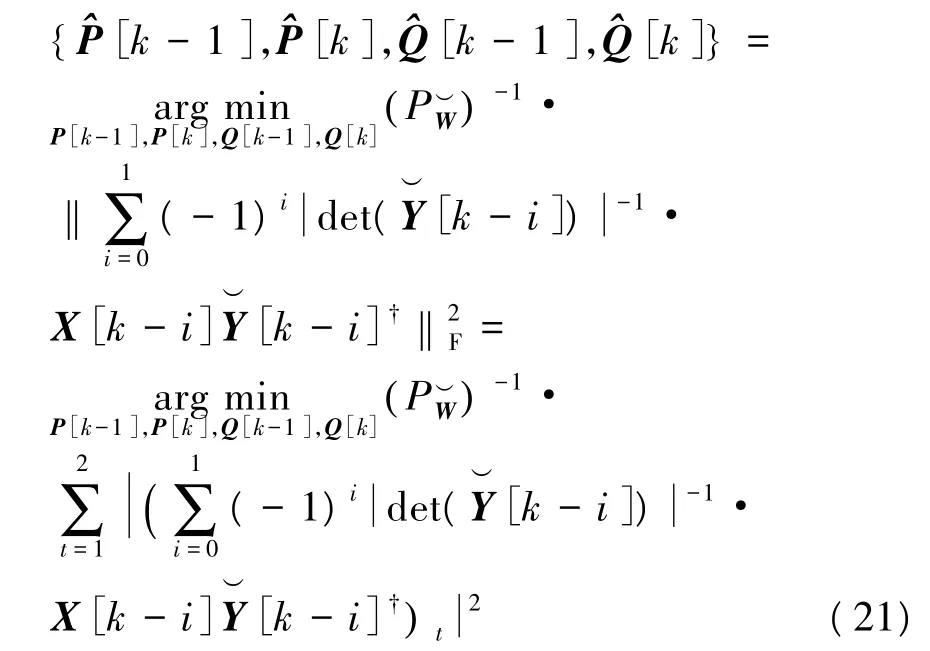
为有效噪声功率，根据式(20)，将有效噪声功率估计为

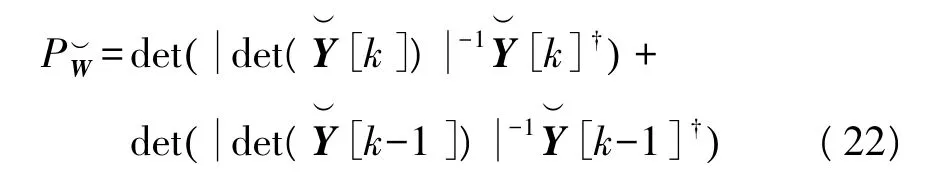
当 k=3时，利用收发双方已知的 C［0］、S［0］、C［1］和S［1］，可以对用户1和用户2在k=2和k=3两个分组时的 OSTBC 矩阵 P［2］、P［3］、Q［2］和Q［3］进行最大似然联合解码;当k=5时，利用已得到的C［3］和S［3］可以得到用户1和用户2在k=4和k=5两个分组时的 OSTBC矩阵 P［4］、P［5］、Q［4］和 Q［5］。以此类推可以对其他发送分组依次进行最大似然联合解码。

以上是同时对两个发送分组进行最大似然判决，也可以每次对一个发送分组进行最大似然判决。当 k=2 时，利用收发双方已知的 C［0］、S［0］、C［1］和S［1］，可以对用户1和用户2在k=2分组时的OSTBC矩阵P［2］和Q［2］进行最大似然联合解码;当k=3 时，利用已得到的 C［1］、C［2］、S［1］和S［2］可以得到用户1和用户2在k=3分组时的OSTBC矩阵P［3］和Q［3］。以此类推可以对其他发送分组依次进行最大似然联合解码。

这种解码算法不仅可以用于2"2的发送矩阵，还可以用于更大阶数的发送矩阵。根据最大比合并规则也可以很容易将接收天线数量推广到大于2的情况下。

2．4 完全差分解码性能优化

在不增加解码复杂度的前提下，这一部分给出了差分解码算法的旋转预编码优化方案。对用户的发送矩阵进行旋转预编码，旋转预编码方案为

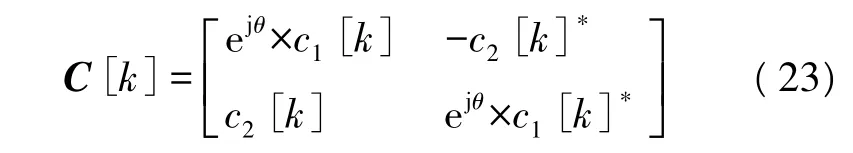
式中，θ为旋转角度。

通过仿真测试，可以找到在BPSK调制条件下的最优旋转角度为π/2。

3 仿真结果及分析

这一部分对提出的差分编解码方案进行了计算机仿真，主要仿真了三种方案，前两种是提出的两用户部分差分编解码方案和两用户完全差分编解码方案，还有一种是文献［15］中的exact方案。同时对差分编解码方案中预编码的旋转角度进行了仿真以寻找最佳旋转角度。

仿真所使用的信道均为准静态平坦瑞利衰落信道，信道衰落系数在一个帧之内是静态的，帧与帧之间的信道衰落系数是相互独立的。每个用户的帧长设为128个符号。仿真使用的调制方式是BPSK。

图2给出的是相关最大似然解码、部分差分解码、完全差分解码和exact解码四种解码算法的性能对比，均采用最优的旋转角度。可以看出，部分差分解码算法的性能要优于完全差分解码和exact解码两种算法。完全差分解码算法较exact解码算法在性能上有了一定的下降。

图2 四种解码算法的性能Fig．2 Performance of the four types of decoder

图3给出的是在不同的旋转角度下完全差分解码算法的性能比较，可以看出最优旋转角度为π/2。

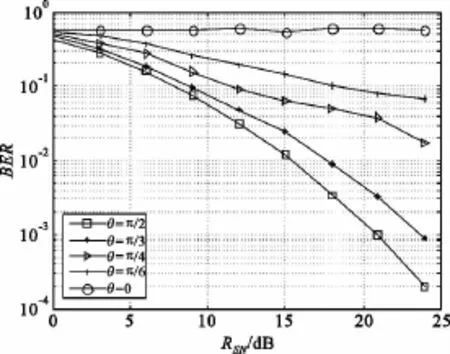
图3 不同旋转角度下完全差分解码算法的性能Fig．3 Performance of the differential decoders at different rotated angles

表1给出了7使用Matlab仿真过程中完全差分解码和exact解码两种算法的复杂度对比。比较的规则是完成两个发送分组的解码所需要的复数加法、复数乘法和矩阵开方的次数。可以看出，完全差分解码算法的复数乘法和复数加法运算次数都要低于exact解码算法，另外exact解码算法还要进行若干次矩阵开方运算。表1的仿真数据说明提出的完全差分解码算法有效降低了解码复杂度。

表1 解码算法复杂度Table 1 Complexity of the differential decoders

4 结语

针对两用户MIMO系统提出了两种基于OSTBC的差分解码算法，一种是部分差分解码算法，利用一个用户的CSI完成对两个用户的解码，一种是低复杂度的完全差分解码算法，在没有CSI的情况下进行解码。为了提高完全差分解码算法的性能，进行了旋转预编码和有效噪声功率估计等优化。仿真结果显示，旋转预编码措施提高了完全差分解码算法的解码性能。最后对完全差分解码算法和exact解码算法进行了算法复杂度分析对比，可以看出，跟exact算法相比，完全差分解码算法有效降低了解码复杂度。

［1］ TELATAR E．Capacity of Multi-Antenna Gaussian Channels［J］．Telecommunications，European Transactions on，1999，10(06):585-595．

［2］ ALAMOUTI S．A Simple Transmit Diversity Technique for Wireless Communications［J］．IEEE Journal on Selected Areas in Communications，1998，16(08):1451-1458．

［3］ TAROKH V，SESHADRI N，CALDERBANK A R．Space-Time Codes for High Data Rate Wireless Communication:Performance Criterion and Code Construction［J］．IEEE Transactions on Information Theory，1998，44(02):744-765．

［4］ TAROKH V，JAFARKHANI H，CALDERBANK A R．Space-Time Block Codes from Orthogonal Designs［J］．IEEE Transactions on Information Theory，1999，45(05):1456-1467．

［5］ JAFARKHANI H．A Quasi-Orthogonal Space-Time Block Code［J］．IEEE Transactions on Communications，2001，49(01):1-4．

［6］ SHAH H K，DANA R K，DASGUPTA K S．Performance Evaluation of QOSTBC and CR-QOSTBC over Correlated Channel［C］//2012 International Conference on Communication Systems and Network Technologies(CSNT)．Rajkot:IEEE，2012:207-210．

［7］ 肖爱民，李辉，戴旭初．一种低复杂度多用户 MIMO预编码方法［J］．通信技术，2012，45(05):8-11．XIAO A，LI H，DAI X．A Low Complexity Precoding Method for Multiuser MIMO［J］．Communications Technology，2012，45(5):8-11．

［8］ HASSIBI B，HOCHWALD B M．How Much Training Is Needed in Multiple-Antenna Wireless Links? ［J］．IEEE Transactions on Information Theory，2003，49(04):951-963．

［9］ TAROKH V，JAFARKHANI H．A Differential Detection Scheme for Transmit Diversity［J］．IEEE Journal on Selected Areas in Communications，2000，18(07):1169-1174．

［10］ JI H，ZAHARIA G，HELARD J F．A New Differential Space-Time Modulation Scheme for MIMO Systems with FourTransmitAntennas［C］//Telecommunications(ICT)，2013 20th International Conference on．Casablanca，Morocco:IEEE，2013:1-5．

［11］ SLIMANE E B，JARBOUI S，BOUALLEGUE A．An Improved Differential Space-Time Block Coding Scheme Based on Viterbi Algorithm［J］．IEEE Communications Letters，2013，17(09):1707-1709．

［12］ TAROKH V，NAGUIB A，SESHADRI N，et al．Combined Array Processing and Space-Time Coding［J］．IEEE Transactions on Information Theory，1999，45(04):1121-1128．

［13］ KAZEMITABAR J，JAFARKHANI H．Multiuser Interference Cancellation and Detection for Users with More Than Two Transmit Antennas［J］．IEEE Transactions on Communications，2008，56(04):574-583．

［14］ BHATNAGAR M R，HJORUNGNES A．Differential Decoder for MAC Based Two-User Communication Systems［J］．IEEE Signal Processing Letters，2010，17(07):687-690．

［15］ BHATNAGAR M R，HJORUNGNES A．Differential Coding for MAC Based Two-User MIMO Communication Systems［J］．IEEE Transactions on Wireless Communications，2012，11(01):9-14．

［16］ JAFARKHANI H．Space-Time Coding:Theory and Practice［M］．Cambridge:Cambridge University Press，2005．

［17］ GRAHAM A．Kronecker Products and Matrix Calculus:with Applications［M］．Chichester:Horwood，1981．