一种单种群混合蛙跳算法

王联国，龚亚星

(1.甘肃农业大学信息科学技术学院，甘肃 兰州 730070；2.甘肃农业大学工学院，甘肃 兰州 730070)

一种单种群混合蛙跳算法

王联国1,2，龚亚星2

(1.甘肃农业大学信息科学技术学院，甘肃 兰州 730070；2.甘肃农业大学工学院，甘肃 兰州 730070)

针对SFLA算法运行速度较慢、在优化部分函数问题时精度不高和易陷入局部最优的缺点，提出了一种单种群混合蛙跳算法SPSFLA。该算法采用单个种群，无需对整个种群进行排序，每个个体通过向群体最优个体和群体中心位置学习进行更新。如果当前个体学习没有进步，则对群体最优个体进行变异，并用变异的结果替代当前个体，加快了算法的运行速度和收敛速度，提高了优化精度。仿真实验结果表明，该算法具有更好的优化性能。

群体智能；混合蛙跳算法；单种群；加速因子；聚群行为

1 引言

混合蛙跳算法SFLA(Shuffled Frog Leaping Algorithm)是2003年由Eusuff M和Lansey K E提出的一种基于群体智能的生物进化算法[1]，在水资源网络分配问题、函数优化、成品油管网优化、组合优化、图像处理、多用户检测、电力系统优化等方面得到了初步应用，并取得了良好的效果。但是，SFLA具有运行速度较慢、求解部分函数优化问题时不够理想的缺陷，因此，很多学者对其进行了改进。文献[2]借鉴差分进化算法DE中DEb1版本的优点，将SFLA与DE有机融合，提出一种蛙跳和差分进化混合算法，有效克服了SFLA容易早熟的缺陷；文献[3]在SFLA深度搜索方向上融合极值动力学优化，对SFLA进行了改进，拓展了算法搜索空间，能够帮助算法跳出局部极值，增强了其全局搜索能力；文献[4]通过对SFLA局部更新策略以及全局信息交流策略的改进，提出了一种能高效求解背包问题的新算法；文献[5]在SFLA中引入自适应因子，提高了个体向局部最优或全局最优个体学习的能力，加快了算法的收敛速度；文献[6]将微粒群算法和SFLA相融合，在蛙群和微粒群两群体独立进化过程中，设计了一种两群之间的信息替换策略以及一种相互协作方式，并适时对其所有个体最好位置进行随机扰动，实验表明新算法性能优越；文献[7]改进了SFLA算法的子群个体优化方式，并提出了最优引导概率和次优引导概率，提高了算法性能；文献[8]提出了一种新的移动距离更新方式对SFLA进行改进，该方式根据新解的适应度高低，决定是否将某分量上一次移动的距离引入本次移动的距离，增强了算法的寻优性能；文献[9]把生物学中的吸引排斥思想引入到混合蛙跳算法中，修正了其更新策略，提高了算法的收敛速度，有效地避免了SFLA早熟收敛的问题，改善了算法对复杂问题的搜索效率。

然而，以上文献对算法的不同改进方法都采用基本SFLA中将种群划分为多个子群的多种群进化模式，虽然多种群能使算法在多个方向进行进化，使其不易陷入局部最优，但是在种群间进行全局信息交流时，不断地排序和划分子群的操作，增加了算法实现的复杂度，耗费大量时间。因此，本文提出一种单种群混合蛙跳算法SPSFLA(Single Population Shuffled Frog Leaping Algorithm)，该算法采用单个种群，无需对整个种群进行排序，每个个体向群体最优个体学习，如果没有进步，则向群体中心位置学习，如果仍然没有进步，则对群体最优个体进行变异，并用变异的结果替代当前个体，从而加快了算法的运行速度和收敛速度，提高了优化精度。此外，通过仿真实验验证了新算法的有效性。

2 单种群混合蛙跳算法

2.1 基本思想

基本混合蛙跳算法采用多个子群，对子群内最差个体通过更新策略进行进化，在进化过程中需要对整个种群进行排序并分组，在每个子群中求子群极值个体和最差个体，计算量大，运行速度较慢。

单种群混合蛙跳算法采用单个种群，无需对整个种群进行排序，每个个体向群体最优个体学习，如果没有进步，则向群体中心位置学习，如果仍然没有进步，则对群体最优个体进行变异，并用变异的结果替代当前个体，因此加快了算法的运行速度和收敛速度。

2.2 更新策略

设青蛙种群规模为F，第i只青蛙的状态向量Xi=(xi1，xi2，…，xin)，n表示变量的维数，青蛙当前所在位置的适应度表示为Y=f(Xi)，其中Y为目标函数值。整个种群迄今为止找到的全局最好适应度的个体表示为Xg=(xg1，xg2，…，xgn) 。整个种群的中心位置为Xc=(xc1，xc2，…，xcn) 。个体i按式(1)向全局最优个体Xg学习，如果得到的新个体newXi=(newxi1，newxi2，…，newxin)优于原来的Xi，则用newXi取代Xi。如果没有改进，则按式(2)向群体中心位置Xc学习，如果得到的新个体newXi优于原来的Xi，则用newXi取代Xi。如果仍然没有改进，则按式(3)随机产生一个新的个体取代原来的Xi。

newxij=xij+rand()×C×(xgj-xij)

(1)

newxij=xij+rand()×C×(xcj-xij)

(2)

(3)

2.3 算法流程

算法流程如下：

Step 1 随机产生种群规模为F只青蛙的种群，设置迭代次数、学习因子等参数；

Step 2 对每只青蛙个体，计算其适应度，找出全局最优个体Xg，计算群体中心位置Xc；

Step 3 对每只青蛙个体按照更新策略更新位置；

Step 4 计算每只青蛙个体的适应度，更新全局最优个体Xg；

Step 5 计算群体中心位置Xc；

Step 6 终止条件是否满足？如果满足，结束迭代，输出最优解Xg，否则转向Step 3。

当种群规模较大时，为了提高计算群体中心位置Xc的速度，按随机抽样方式选取M个个体，计算M个个体的中心位置，并用其代替群体中心位置Xc。

2.4 时间复杂度分析

SPSFLA在实现的过程中，有以下几个主要操作：

(1)初始化F个个体，每个个体是D维，其时间复杂度为O(D·F)；

(2)对F个个体计算适应度值，适应度函数的复杂度一般都是O(D)，所以其时间复杂度为O(D·F)；

(3)在一次迭代中，对已经计算出的F个个体的适应度值进行统计，找出全局最优个体，其时间复杂度为O(F)，并计算群体中心位置，其时间复杂度为O(D·F)；

(4)在一次迭代中，需要对F个个体的每一维进行更新，故其时间复杂度为O(D·F)；

(5)在一次迭代后，判断中止条件，时间复杂度为O(1)。

设最大迭代次数为Itmax，当Itmax足够大时，低次幂影响可忽略不计，因此SPSFLA的时间复杂度为O(Itmax·D·F)。而在基本SFLA中，对F个个体按照适应度值进行降序排列的操作，时间复杂度为O(D·F·F)，系为其最大时间复杂度，若设其混合迭代次数为Itmax，则SFLA的时间复杂度为O(Itmax·D·F2)。这说明，SPSFLA较之SFLA

具有较小的时间复杂度。

3 仿真实验

3.1 实验设计

本文分别用SFLA、文献[9]提出的ISFLA以及SPSFLA求八个基准测试函数的最小值，进行对比实验，以评价改进算法的优化性能。

实验中，各算法的参数设置如下：对于SPSFLA，种群规模F=200，学习因子C=2。对于SFLA和ISFLA，种群规模仍为200只青蛙，但要将其分为20个子群，每个子群含10只青蛙，子群内更新迭代次数为10，步长Dmax=Xmax/5(Xmax为搜索范围的最大值)，最大迭代次数均设为500。由于SFLA和ISFLA总的迭代次数为20个子群×每个子群10次迭代×500次迭代=100000，SPSFLA总的迭代次数为200个个体×每个个体1次迭代×500次迭代=100000，三种算法总的迭代次数相同，因此具有可比性。八个测试函数及其实验的相关参数见表1。

算法的性能评估采用如下方法：固定进化迭代次数，评估其收敛速度、精度、稳定性和达到目标精度的成功率，其中，成功率=达到目标精度的运行次数/总实验次数。各算法的最终测试结果采用独立运行30次后的平均值。

Table 1 Parameters of test functions

3.2 实验结果及分析

表2为30次实验所得的三个算法的平均值、标准差、成功率以及平均运行时间。可以看出，除了f4函数外，SPSFLA对于其余七个函数的平均最优值、标准差均好于SFLA和ISFLA，尤其对于f3函数，SPSFLA找到了其全局最优值0；对于f4函数，虽然SPSFLA的平均最优值及标准差略逊于ISFLA，但要比SFLA好得多。这说明SPSFLA的求解精度较高，稳定性好。成功率方面，SPSFLA对于除f4函数以外的其它七个函数均能达到100%，尤其对于f1、f5、f8函数在其余两种算法都为0%的成功率时，SPSFLA表现出了更强的寻优能力及稳定性。此外，SPSFLA算法运行的平均时间都要远少于SFLA和ISFLA。综上所述，总体上，SPSFLA求解精度高、稳定性好、运行速度快。

Table 2 Experimental results of three algorithms

图1～图8是函数f1～f8采用三种算法运行30次后得到的平均极值的进化曲线，在图1～图7中，纵坐标用函数平均极值的常用对数表示，在图8中，因f8函数的极值为负，纵坐标直接用函数的平均极值表示，各图中横坐标均为迭代次数。当函数值为0时，则对函数值均加上10-5作为截止值。从图中可以看出，对所有八个函数而言，SPSFLA总能最先收敛，除了对f4函数的最终收敛值略差于ISFLA，对其它函数，SPSFLA总是收敛于更好的解，这说明，SPSFLA收敛速度较快且优化精度较高。

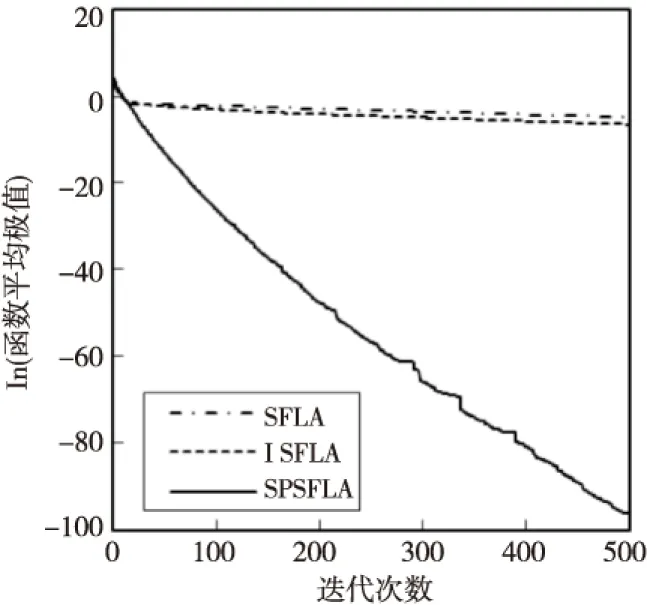
Figure 1 Average evolutionary curve of f1图1 图1 函数f1平均极值的进化曲线

Figure 2 Average evolutionary curve of f2图2 函数f2平均极值的进化曲线

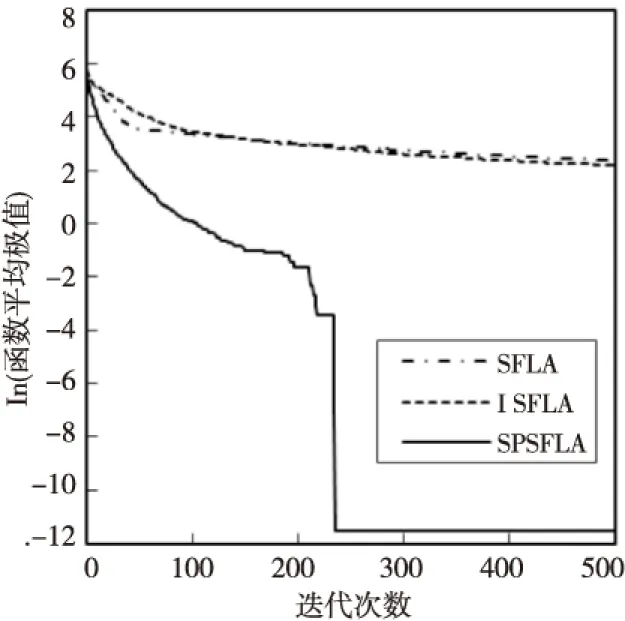
Figure 3 Average evolutionary curve of f3图3 函数f3平均极值的进化曲线

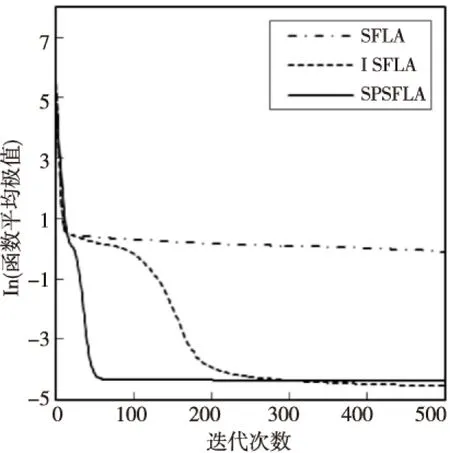
Figure 4 Average evolutionary curve of f4图4 函数f4平均极值的进化曲线

Figure 5 Average evolutionary curve of f5图5 函数f5平均极值的进化曲线

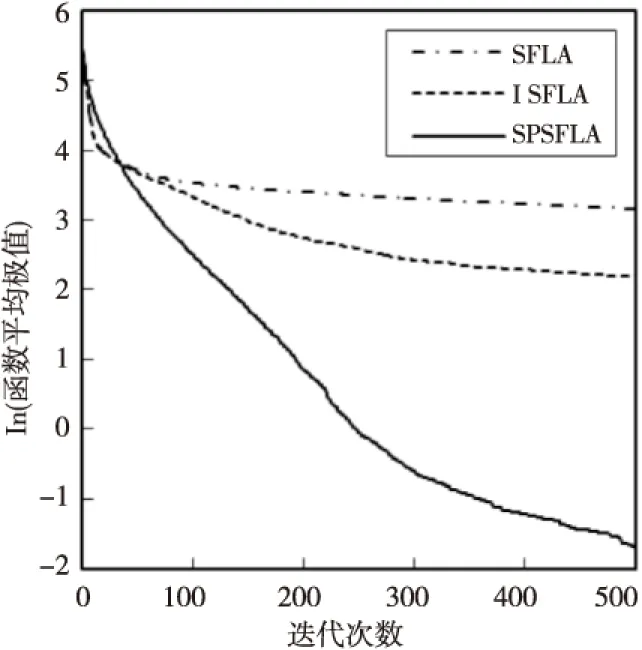
Figure 6 Average evolutionary curve of f6图6 函数f6平均极值的进化曲线

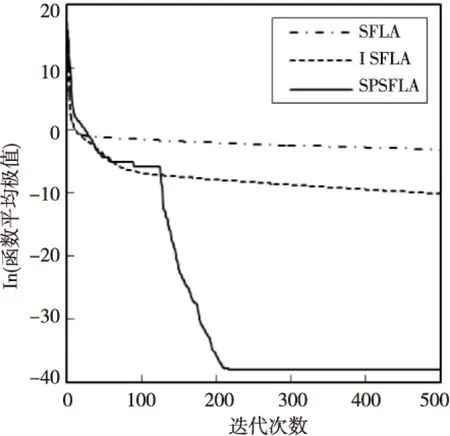
Figure 7 Average evolutionary curve of f7图7 函数f7平均极值的进化曲线

Figure 8 Average evolutionary curve of f8图8 函数f8平均极值的进化曲线

4 结束语

针对SFLA算法运行速度慢、对部分函数优化精度不高等问题，提出了一种单种群混合蛙跳算法，该算法采用单个种群，结合人工鱼群算法中的聚群行为思想，对群体极值进行变异并替代随机算子，加快了算法的运行速度和收敛速度，提高了算法的优化精度。仿真实验结果表明，该算法具有更好的优化性能。

[1] Eusuff M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Water Resources Planning and Management,2003,129 (3):210-225.

[2] He Bing, Che Lin-xian, Liu Chu-sheng. Novel hybrid shuffled frog leaping and differential evolution algorithm[J]. Computer Engineering and Applications,2011,47(18):4-8. (in Chinese)

[3] Luo Jian-ping, Chen Min-rong. Study on trajactory and convergence analysis of shuffled frog leaping algorithm and its improved algorithm[J]. Signal Processing, 2010,26(9):1428-1433. (in Chinese)

[4] Li Z F, Zhou Y, Cheng P. An improved shuffled frog leaping algorithm for knapsack problem[J]. Advances in Intelligent and Soft Computing,2012(169):299-303.

[5] Dai Yong-qiang, Wang Lian-guo, Shi Qiu-hong, et al. Performance analysis of improved SFLA and the application in economic dispatch of power system[J]. Power System Protection and Control, 2012,40(10):77-83. (in Chinese)

[6] Sun Hui, Long Teng, Zhao Jia. Swarm intelligence algorithm based on combination of shuffled frog leaping algorithm and particle swarm optimization[J]. Journal of Computer Applications, 2012,32(2):428-431. (in Chinese)

[7] Zhang J M, Wu C C. Improved shuffled frog leaping algorithm and its application[J]. Applied Mechanics and Materials, 2012(155/156):92-96.

[8] Zheng Shi-lian,Lou Cai-yi,Yang Xiao-niu.Cooperative spectrum sensing for congnitive radios based on a modified shuffled frog leaping algorithm[J]. Acta Physica Sinica, 2010,59(5):3611-3617. (in Chinese)

[9] Zhao Peng-jun, Liu San-yang. Shuffled frog leaping algorithm for solving complex functions[J]. Application Research of Computers, 2009,26(7):2435-2437. (in Chinese)

附中文参考文献：

[2] 何兵,车林仙,刘初升.一种蛙跳和差分进化混合算法[J].计算机工程与应用,2011,47(18):4-8.

[3] 骆剑平,陈泯融.混合蛙跳算法及其改进算法的运动轨迹及收敛性分析[J].信号处理,2010,26(9):1428-1433.

[5] 代永强,王联国,施秋红,等.改进的混合蛙跳算法性能分析及其在电力系统经济调度中的应用[J].电力系统保护与控制,2012,40(10):77-83.

[6] 孙辉,龙腾,赵嘉.基于微粒群与混合蛙跳融合的群体智能算法[J].计算机应用,2012,32(2):428-431.

[8] 郑仕链,楼才义,杨小牛. 基于改进混合蛙跳算法的认知无线电协作频谱感知[J].物理学报,2010,59(5):3611-3617.

[9] 赵鹏军,刘三阳.求解复杂函数优化问题的混合蛙跳算法[J].计算机应用研究,2009,26(7):2435-2437.

WANG Lian-guo,born in 1968,PhD,professor,his research interest includes intelligent information processing.

龚亚星(1990-),女,甘肃西和人，硕士生,研究方向为计算智能，农业电气化与自动化。E-mail:yaxing918@126.com

GONG Ya-xing,born in 1990,MS candidate,her research interests include computational intelligence, agricultural electrification and automation.

A single population shuffled frog leaping algorithm

WANG Lian-guo1,2，GONG Ya-xing2
(1.College of Information Science and Technology,Gansu Agricultural University,Lanzhou 730070;2.College of Engineering,Gansu Agricultural University,Lanzhou 730070,China)

Aiming at the shortcomings of shuffled frog leaping algorithm(SFLA) such as ease of trapping into local optimum, low optimization precision and slow speed when it is used to optimize some functions, a Single Population Shuffled Frog Leaping Algorithm (SPSFLA) is proposed. Without sorting the whole population, this new algorithm adopts single population. The individuals are updated by learning from the global best individual and the global middle position. If the current individual is not improved, the global best individual will be mutated and the current individual will be replaced by the new one. Those enhance the running speed, the convergence rate and the optimization precision of SPSFLA. The simulation results show that the improved algorithm has better optimization performance.

swarm intelligence;shuffled frog leaping algorithm;single population;acceleration factor;swarm behavior

2012-10-15;

2013-01-09

国家自然科学基金资助项目(61063028)；甘肃省教育信息化发展战略研究项目(2011)

1007-130X(2014)03-0463-06

TP18

A

10.3969/j.issn.1007-130X.2014.03.015

王联国(1968-),男,甘肃临夏人，博士，教授，研究方向为智能信息处理。E-mail:wanglg@gsau.edu.cn

通信地址：730070 甘肃省兰州市安宁区甘肃农业大学信息科学技术学院

Address:College of Information Science and Technology,Gansu Agricultural University,Anning District,Lanzhou 730070,Gansu,P.R.China