带形状参数的Bernstein-Bézier曲面*
严兰兰
(东华理工大学理学院,江西 抚州 344000)
带形状参数的Bernstein-Bézier曲面*
严兰兰
(东华理工大学理学院,江西 抚州 344000)
虽然三角域上的曲面造型方法能有效解决不规则产品的几何造型问题, 在实际工程中有着广泛的应用, 但由于其结构的特殊性和复杂性, 目前对三角域曲面的扩展研究并不多。为了丰富三角域曲面的理论, 针对如何增强三角域曲面形状表示的灵活性进行了专门的研究。首先构造了一组三角域上含一个参数的四次多项式基函数, 它是三角域上二次Bernstein基函数的扩展。然后用递推的方式定义了三角域上含一个参数的n+2次多项式基函数, 它是三角域上n次Bernstein基函数的扩展。基于新的n+2次多项式基函数, 定义了相应的n阶三角域曲面。分析了基函数和曲面的性质, 新曲面不仅具备三角域上Bernstein-Bézier曲面的基本性质, 而且还可以在不改变控制顶点的情况下, 通过改变参数的值来自由调整曲面的形状。
曲面设计;形状参数;三角域;Bernstein-Bézier曲面
1 引言
Bézier方法因为简单、直观而成为计算机辅助几何设计中最常用的造型方法之一。传统的Bézier方法既包括Bézier曲线、四边域上的张量积Bézier曲面, 还包括三角域上的Bernstein-Bézier曲面。这三者在形状表示方面各有各的优点, 但它们有一个共同的缺点, 就是不具备形状可调性, 即在控制顶点固定的情况下, 它们的形状是无法改变的。针对Bézier曲线的这一缺点, 目前已经有很多文献提出了改进方法[1~4]。这些文献中的方法可以归纳为, 通过构造含参数的、性质类似于Bernstein基函数的新的基函数, 使得由之定义的曲线在具备Bézier曲线基本性质的同时, 又具备形状可调性。由于四边域上的张量积Bézier曲面是Bézier曲线向曲面的直接推广, 所以这些文献中的方法在克服Bézier曲线的缺点的同时, 也克服了张量积Bézier曲面的缺点。但是,由于定义在三角域上的Bernstein-Bézier曲面结构的特殊性, 这些文献中的方法不能直接推广至三角域曲面, 因此, 必须单独为三角域曲面构造含参数的基函数, 使得由之定义的曲面具备形状可调性。
但是,目前关于这方面的研究成果很少, 迄今为止, 仅见到以下成果:邬弘毅等[5]给出的三角域上带多个形状参数的Bézier曲面, 由于该方法中的参数较多, 无疑增加了构造曲面的复杂性。曹娟等[6]给出的三角域上带一个形状参数的三次Bernstein-Bézier曲面的扩展曲面, 于立萍[7]给出的三角域上带两个形状参数的三次Bernstein-Bézier曲面的扩展曲面, 都具有灵活的形状, 但这两种方法都仅仅只解决了三次Bernstein-Bézier曲面的形状调整问题, 不具备一般性。吴晓勤等[8]、CAO Juan等[9]、Yan Lan-lan等[4]给出的三角域上带一个形状参数的任意n次Bernstein-Bézier曲面的扩展曲面, 都较好地解决了三角域曲面的形状调整问题, 并且都具有一般性。
为了提供更多的含参数的三角域曲面造型方法, 进一步充实现有的CAD系统, 本文在文献[4,8,9]的基础上构造了一种新的结构和性质类似于Bernstein-Bézier曲面的三角域曲面, 并通过实例表明该方法是正确有效的。
2 基函数的构造与性质
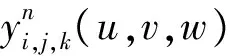
(1)
(2)
类Bernstein-Bézier基函数具有下列性质:

证明用数学归纳法。当n=2时, 类Bernstein-Bézier基函数可以表示成四次Bernstein-Bézier基函数的线性组合, 即:
(3)

假设r阶类Bernstein-Bézier基函数非负, 当n=r+1时, 由式(2)有:

□
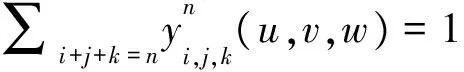
证明用数学归纳法。当n=2时, 由式(3)有:
假设当n=r时规范性成立, 当n=r+1时, 由式(2)有:
证毕。
□
(3) 轮换对称性。对u、v、w≥0,u+v+w=1,有:
(4)
其中,i、j、k∈N,i+j+k=n,n≥2。
证明用数学归纳法。当n=2时, 由式(3)以及四次Bernstein-Bézier基函数的对称性, 可知式(4)对n=2成立。假设式(4)对n=r成立, 由这一假设以及式(2), 可知当n=r+1时, 有:
其它几种关系类似可证。
□
(4) 角点性质。当n≥2时, 对于i、j、k∈N,i+j+k=n, 有:
(5)
证明用数学归纳法。当n=2时, 对式(1)直接计算可知式(5)的正确性。假设式(5)对n=r成立, 当n=r+1时,
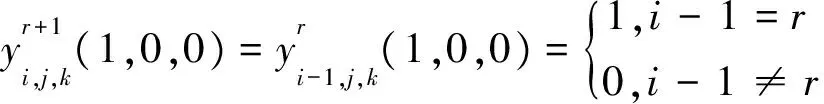
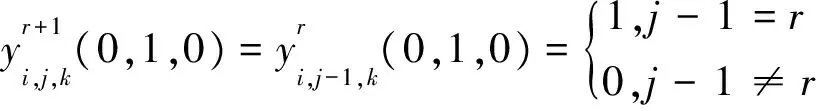
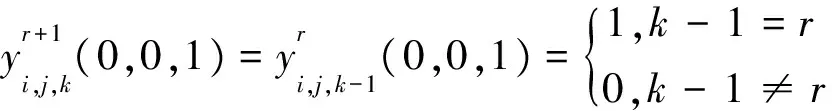
这些表明式(5)对n=r+1成立。证毕。
□
(5)角点导数。对u、v、1-u-v≥0,i、j、k∈N,i+j+k=n,n≥2, 有:
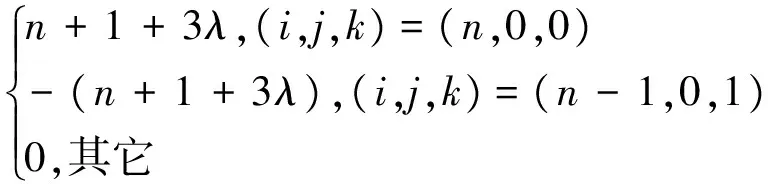
(6)

(7)
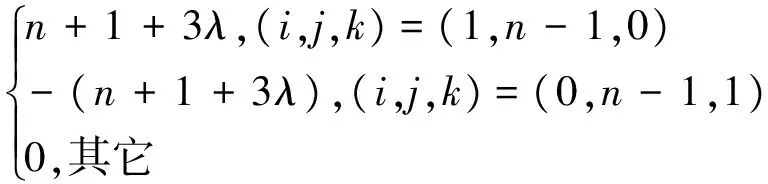
(8)

(9)

(10)

(11)
证明用数学归纳法。当n=2时, 直接计算易知式(6)~式(11)对n=2成立。假设式(6)对n=r成立, 当n=r+1时, 由式(2)有:
(12)
在式(12)两端对u求导, 得到:
取点(u,v,1-u-v)=(1,0,0), 得到:
由式(5)中所列的在角点(1,0,0)处的性质, 以及归纳假设, 可得:
① 若(i-1,j,k)=(r,0,0), 即(i,j,k)=(r+1,0,0), 则:

② 若(i,j,k-1)=(r,0,0), 即(i,j,k)=(r,0,1), 则:
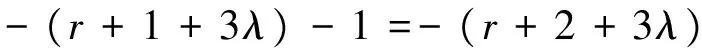
③ 若(i-1,j,k)≠(r,0,0)且(i,j,k-1)≠(r,0,0), 即(i,j,k)≠(r+1,0,0)且(i,j,k)=(r,0,1), 则:
这些结论表明式(6)对n=r+1成立。类似可证式(7)~式(11)也对n=r+1成立。
□
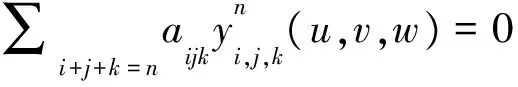
证明充分性是显然的。下面用归纳法证明必要性。假设对所有的u、v、w≥0,u+v+w=1,有:
(13)
其中aijk∈R,i、j、k∈N,i+j+k=2。将式(3)代入式(13)并整理, 得到:
由四次Bernstein-Bézier基函数的独立性, 可得式(14)。
将式(14)中的式(14-a)代入式(14-b)中, 可得式(15)。
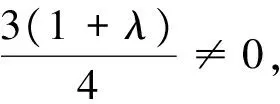
假设r阶类Bernstein-Bézier基函数线性无关, 下面证明r+1阶类Bernstein-Bézier基函数也线性无关。
(14)
(15)
假设对所有的u、v、w≥0,u+v+w=1, 有:
(16)
其中aijk∈R,i、j、k∈N,i+j+k=r+1。将式(2)代入式(16)并整理, 得到:
由u、v、w的任意性可得:
(17)
由归纳假设及式(17)中的式(17-a)可知, 对所有i、j、k∈N,i+j+k=r+1, 当i≥1时,aijk= 0;由式(17)中的式(17-b)可知, 对所有i、j、k∈N,i+j+k=r+1, 当j≥1时,aijk=0; 由式(17)中的式(17-c)可知, 对所有i、j、k∈N,i+j+k=r+1, 当k≥1时,aijk=0。故对所有的i、j、k∈N,i+j+k=r+1, 有aijk=0。这表明r+1阶类Bernstein-Bézier基函数线性无关。
□
3 曲面的构造与性质
定义2给定(n+1)(n+2)/2个控制顶点Vi,j,k∈R3(i、j、k∈N,i+j+k=n), 三角域D= {(u,v,w)|u、v、w≥0,u+v+w=1},其中(u,v,w)为D中点的重心坐标, 称:
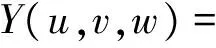
(18)
为定义在三角域D上的带参数的n阶类Bernstein-Bézier曲面。
由类Bernstein-Bézier基函数的性质, 容易推出类Bernstein-Bézier曲面具有下列性质:
(1) 凸包性。类Bernstein-Bézier曲面位于控制网格所在的凸包内。
(2) 仿射不变性。类Bernstein-Bézier曲面的形状和位置与坐标系的选择无关, 对曲面作仿射变换, 只需对其网格作此仿射变换。
(3) 角点插值性。曲面的3个角点分别插值于控制网格的3个角点, 即:
(4) 角点切平面。曲面在角点(1,0,0)、(0,1,0)、(0,0,1)处的切平面分别为由控制顶点Vn,0,0、Vn-1,1,0、Vn-1,0,1;V0,n,0、V1,n-1,0、V0,n-1,1;V0,0,n、V1,0,n-1、V0,1,n-1张成的平面。
(5) 形状可调性。给定控制顶点, 普通Bernstein-Bézier曲面的形状就唯一确定了, 而对于类Bernstein-Bézier曲面而言, 即使不改变控制顶点, 其形状依然可以通过改变λ的值进行调整。
图1和图2给出了在相同的控制网格下, Bernstein-Bézier曲面与类Bernstein-Bézier曲面的对照图。其中图1a、图2a分别为二次、三次Bernstein-Bézier曲面, 图1b~图1f、图2b~图2f分别为带参数λ=-1、-3/4、-1/2、-1/4、0的二阶、三阶类Bernstein-Bézier曲面。从图中可以看出,λ越大, 类Bernstein-Bézier曲面越接近其控制网格。
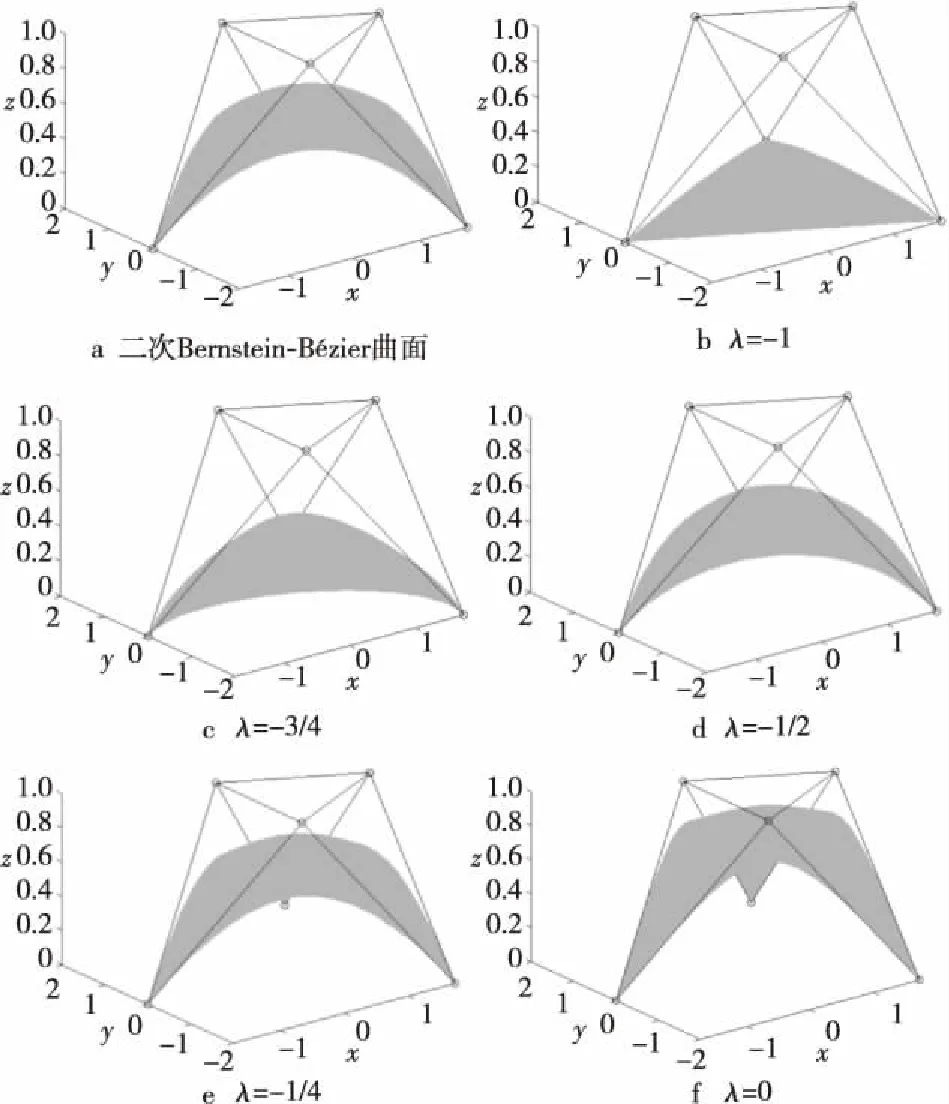
Figure 1 Contrast of the quadratic Bernstein-Bézier surface and the Bernstein-Bézier surface of order two图1 二次Bernstein-Bézier曲面与 二阶类Bernstein-Bézier曲面的对照图

Figure 2 The contrast of cubic Bernstein-Bézier surface and the Bernstein-Bézier surface of order three图2 三次Bernstein-Bézier曲面与 三阶类Bernstein-Bézier曲面的对照图
(6)递推求值算法。给定参数u、v、w(u、v、w≥ 0,u+v+w=1), 可以用下面的算法来计算n阶类Bernstein-Bézier曲面上相应的点Y(u,v,w)。
为了简洁, 用τ表示u,v,w, 则:


当l=n-1时,
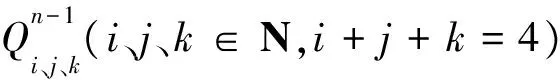
4 参数λ对曲面形状的影响
在工程实际中主要应用的是低阶的曲面, 为了方便应用, 下面分析参数λ的取值对二阶、三阶类Bernstein-Bézier曲面形状的影响。
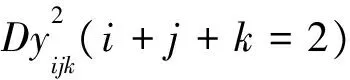
上面的结果表明,y200、y020、y002是关于λ的递减函数, 而y110、y011、y101是关于λ的递增函数。基函数的这种性质反映在二阶类Bernstein-Bézier曲面的图形上的特点是:在参数λ允许的范围内,λ的值越大, 曲面越远离由三个角点V200、V020、V002确定的平面, 同时越接近由三个中间点V110、V011、V101确定的平面, 见图1b~图1f。
由式(1)和式(2)可知,当n=3时,
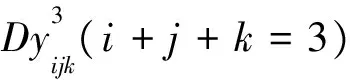
(19)
式(19)表明y300、y030、y003是λ的递减函数。y111是λ的递增函数。当w=0时,y210、y120是λ的递增函数; 当u=0时,y021、y012是λ的递增函数; 当v=0时,y102、y201是λ的递增函数。基函数的这种性质反映在三阶类Bernstein-Bézier曲面的图形上的特点是:在参数λ允许的范围内,λ的值越大, 曲面越远离由三个角点V300、V030、V003确定的平面, 越接近中心点V111, 同时三条边界曲线分别越接近相应的控制边V210V120、V021V012、V102V201,见图2b~图2f。
5 曲面的造型实例
本文提出的三角域曲面造型方法具有一般性, 任给(n+1)(n+2)/2个控制顶点(n≥2), 选择恰当的参数λ, 便可以构造出想要的曲面。图3~图5给出了类Bernstein-Bézier曲面的造型实例。图3中的两张曲面均取参数λ=-1/2;图4、图5中的曲面均取参数λ=0。
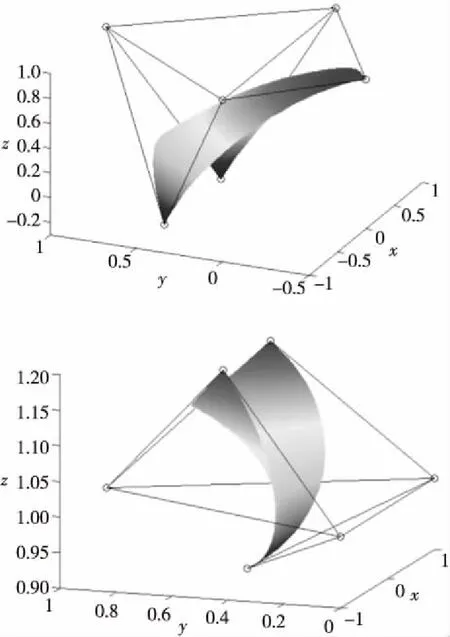
Figure 3 Bernstein-Bézier-like surfaces of order two图3 二阶类Bernstein-Bézier曲面

Figure 4 Bernstein-Bézier-like surfaces of order three图4 三阶类Bernstein-Bézier曲面

Figure 5 Bernstein-Bézier-like surfaces of order four图5 四阶类Bernstein-Bézier曲面
6 结束语
通过提高多项式的次数, 本文首先对三角域上的二次Bernstein-Bézier基函数进行推广, 然后借助递推公式对三角域上任意次的Bernstein-Bézier基函数进行推广。新的基函数具有Bernstein-Bézier基函数的非负性、规范性、对称性等诸多良好性质, 又因为新的基函数中含有参数, 所以由之定义的新的三角域曲面在具备普通Bernstein-Bézier曲面的凸包性、仿射不变性、角点插值性等优良性质的同时, 又具备了形状可调性。要想改变新曲面的形状, 只需简单地改变形状参数的值即可。形状参数越大, 曲面越逼近控制网格, 形状参数的这一直观的几何意义可以帮助我们快速确定合适的参数值来得到想要的形状。
虽然本文提出的类Bernstein-Bézier曲面具备很多优点, 但由于单一的曲面片难以表示复杂的形状, 所以为了使新曲面能更好地服务于工程实际, 研究该曲面间的光滑拼接条件迫在眉睫, 而这也正是下一步的研究内容。
[1] Wang Wen-tao, Wang Guo-zhao. Bézier curves with shape parameter [J]. Journal of Zhejiang University:Science A, 2005, 6(6):497-501.
[2] Wu Xiao-qin. Bézier curve with shape parameter [J]. Journal of Image and Graphics, 2006, 11(2):269-274. (in Chinese)
[3] Han Xi-an, Ma Yi-chen, Huang Xi-li. A novel generalization of Bézier curve and surface [J]. Journal of Computational and Applied Mathematics, 2008, 217(1):180-193.
[4] Yan Lan-lan, Liang Jiong-feng. An extension of the Beizer model [J]. Applied Mathematics and Computation, 2011, 218(6):2863-2879.
[5] Wu Hong-yi, Xia Cheng-lin. Extensions of Bézier curves and surfaces with multiple shape parameters [J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(12):2607-2612. (in Chinese)
[6] Cao Juan, Wang Guo-zhao. Extension of the cubic Bernstein-Bézier surfaces over the triangular domain[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(9):1403-1407. (in Chinese)
[7] Yu Li-ping. Extension of Bézier surface with two shape parameters over the triangular domain [J]. College Mathematics, 2008, 24(5):58-62. (in Chinese)
[8] Wu Xiao-qin,Han Xu-li.Bézier triangular patch with a shape parameter[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(11):1735-1740. (in Chinese)
[9] Cao Juan, Wang Guo-zhao. An extention of Bernstein-Bézier surface over the triangular domain [J]. Progress in Natural Science, 2007, 17 (3):352-357.
附中文参考文献:
[2] 吴晓勤. 带形状参数的Bézier曲线[J]. 中国图象图形学报, 2006, 11(2):269-274.
[5] 邬弘毅, 夏成林. 带多个形状参数的Bézier曲线与曲面的扩展[J]. 计算机辅助设计与图形学学报, 2005, 17(12):2607- 2612.
[6] 曹娟, 汪国昭. 三角域上三次Bernstein-Bézier参数曲面的扩展[J]. 计算机辅助设计与图形学学报, 2006, 18(9):1403- 1407.
[7] 于立萍. 三角域上带两个形状参数的Bézier曲面的扩展[J]. 大学数学, 2008, 24(5):58-62.
[8] 吴晓勤, 韩旭里. 带有形状参数的Bézier三角曲面片[J]. 计算机辅助设计与图形学学报, 2006, 18(11):1735-1740.
YANLan-lan,born in 1982,MS,lecturer,her research interest includes computer aided geometric design.
Bernstein-Béziersurfacewithshapeparameters
YAN Lan-lan
(College of Science,East China Institute of Technology,Fuzhou 344000,China)
Because the surface modeling method over the triangular domain can effectively solve the geometric modeling problem of irregular products, it is widely used in practical engineering. However, due to the particularity and complexity of the structure, there are not many studies on the extension of triangular surface at present. In order to enrich the theory of triangular surface, the paper carries out a specialized research on how to enhance the flexibility of shape representation of triangular surface. Firstly, a set of polynomial basis functions of degree four with one parameter over the triangular domain is constructed, which is an extension of the quadratic Bernstein basis function over the triangular domain. Secondly, based on it, the basis functions of degreen+2 with one parameter is defined by a recursive way, which is an extension of the Bernstein basis function of degreen. Thirdly, based on the new basis function of degreen+2, the triangular surface of ordernis defined. The properties of the basis functions and the surfaces are analyzed. The new surfaces not only have the basic properties of the Bernstein-Bézier surfaces, but also enjoy shape adjustable property.
surface design;shape parameter;triangular domain;Bernstein-Bézier surface
2012-09-20;
:2012-12-21
国家自然科学基金资助项目(11261003)
1007-130X(2014)02-0317-08
TP391.4
:A
10.3969/j.issn.1007-130X.2014.02.021

严兰兰(1982-),女,湖北浠水人,硕士,讲师,研究方向为计算机辅助几何设计。E-mail:yxh821011@aliyun.com
通信地址:344000 江西省抚州市学府路56号东华理工大学理学院Address:College of Science,East China Institute of Technology,56 Xuefu Rd,Fuzhou 344000,Jiangxi,P.R.China

