UCW-hyperbolic空间中一类映射的不动点性质

崔云安，赵霞霞，张敬信

(哈尔滨理工大学 应用数学系，哈尔滨150080)

1 预备知识

定义1.1 设C是度量空间(X，d)的一个非空子集，称映射T:C→C是非扩张的，是指：对所有的x,y∈C，d(Tx,Ty)≤d(x,y)成立.

定义1.2 设C是度量空间(X,d)的一个非空子集，称映射T:C→C是平均非扩张的，是指：对任意的a,b≥0,a+b≤1,

d(Tx,Ty)≤ad(x,y)+bd(x,Ty)

成立,其中：x,y∈C.

定义1.3 设C是度量空间(X,d)的一个非空子集，称映射T∶C→C是渐近平均非扩张的，是指：对所有的x,y∈C，

d(Tx,Ty)≤and(x,y)+bn(x,Ty)

在众多的关于非扩张映射的研究中,其中一个十分重要的结果就是1968年由Browder提出的半闭原理[1].

2 主要定理

本文考虑的Hyperbolic空间是Kohlenbac U[2]于2005年引入的. 为了区分Gromov hyperbolic空间和其他“Hyperbolic空间”见文献[3-4], 我们用W-hyperbolic空间来表述.

定义2.1 设(X,d)为距离空间，凸映射W∶X×X×[0,1]→X满足：

(W1)d(z,W(x,y,λ))≤(1-λ)d(z,x)+λd(z,y)；

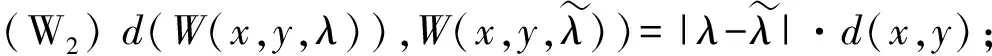
(W3)W(x,y,λ)=W(y,x,1-λ)；

(W4)d(x,z,λ),W(y,w,λ))≤(1-λ)d(x,y)+λd(z,w).

则称(X,d,W)为W-hyperbolic空间.

若(X,d,W)满足条件(W1)则称为凸距离空间.

若(X，d,W)满足条件(W1)-(W3) , 则为GOEBEL K和Kirk W A意义下的hyperbolic型空间[5].

定义2.2[5]W-hyperbolic空间(X,d,W)称为严格凸的，是指对任意的x,y∈X以及λ∈[0,1], 存在唯一元z∈X满足

d(z,x)=λd(x,y)，d(z,y)=(1-λ)d(x,y).

定义2.3[6]称W-hyperbolic空间(X,d,W)是一致凸的，是指若对任意的r>0以及ε∈(0,2]，存在θ∈(0,1]使得对任意的a,x,y∈X，

对任意给定的r>0和ε∈(0，2]，定义映射η：(0，∞)×(0，2]→(0，1]为η(r,ε):=θ，则称该映射η为一致凸模.若η关于r递减(对于固定的ε)，则称η是单调的.

引理2.1[6]设(X,d,W)为一致凸W-hyperbolic空间，其一致凸模为η则对任意的r>0，ε∈(0,2]，λ∈(0,1]以及a,x,y∈X,

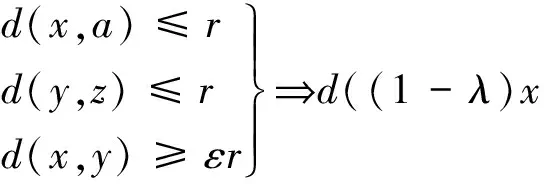
(1-2λ(1-λ)η(r,ε))r.

为了方便, 我们简记一致凸W-hyperbolic空间为UCW-hyperbolic空间, UCW-hyperbolic空间是严格凸的.

命题2.1 (非空交性质)设(X,d,W)为完备的具有单调一致凸模的UCW-hyperbolic空间, 则X中任意递降非空有界闭凸集列的交非空.

证明对每一个y∈C，定义集合

Ay={b∈R+:存在x∈C,k∈N满足d(Tiy,x)≤b,∀i≥k}

可知，diam(C)∈Ay，因此Ay非空. 令∂y:infAy. 则对任意θ>0，存在bθ∈Ay满足bθ<∂y+θ. 从而，存在x∈C以及k∈N满足

d(Tiy,x)≤bθ<∂y+θ，∀i≥k

(1)

显然，∂y≥0. 下面分两种情况进行讨论：

情形1:∂y=0.

令ε>0. 在式(1)中取, 则存在x∈C及k∈N，满足对∀m,n≥k，

θ=ε/2d(Tmy,Tny)≤d(Tmy,x)+d(Tny,x)

(2)

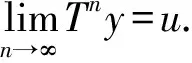
根据T的定义有:

d(Tny,Tu)≤and(Tn-1y,u)+bnd(Tn-1y,Tu)

(3)

两边对n取极限,可得d(u,Tu)≤bd(u,Tu).由于b<1,从而Tu=u即u是T的不动点.

情形2:∂y>0.

对每一个n≥1，定义

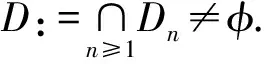
(4)

用反证接下来法证明对任意的x∈D，{Tnx}是一个Cauchy列. 否则，存在ε0>0及N0∈N使得

d(Tmx,Tnx)≥ε0∀m,n≥N0,m≠n，

(5)

(6)

在式(4)中令θ=θ0/2，则存在K∈N满足

(7)

对给定的，m,n≥N0,m≠n，由式(6)及T的定义，当m0>m+k时，

=∂y+θ0

(8)

其中C(m,r)表示从m中取出r个元素的组合数.类似地，对m0>n+K时，

d(Tnx,Tm0y)≤∂y+θ0

(9)

令k0∈N满足k0≥max{m,n}+K，由式(5)、(8)、(9)可得

d(Tmx,Tm0y)≤∂y+θ0

d(Tnx,Tm0y)≤∂y+θ0

d(Tmx,Tnx)≥ε0

再由X是一致凸且η是单调的，可以得到

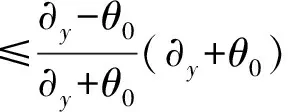
=∂y+θ0

注意到情形1后面的证明，存在u∈C满足Tu=u.

接下来证明UCW-hyperbolic空间中渐近平均非扩张映射的半闭原理, 在证明之前需要定义以下符号：

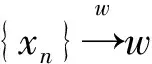
证明由于{xn}是T的渐近不动点序列，则有

(10)

下面用归纳法证明对任意的x∈C，Φ(Tmx)≤Φ(x).

当m=1时，根据的定义及式(10)可得：

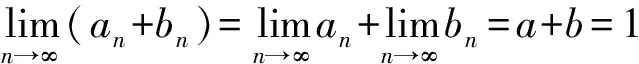
下面证明对任意正整数m，Φ(Tmx)≤Φ(Tx).

假设当i≤m-1时，Φ(Ti-1)≤Φ(Tx)成立，从而

(11)

下面证明{Tmω}是Cauchy列.

假设{Tmω}不是Cauchy列，则存在ε0>0及N0∈N满足

d(Tiω,Tjω)≥ε0,i,j≥N0，

(12)

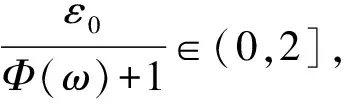
(13)

由Φ的定义和式(11)对上述的θ0，存在M∈N满足

d(Tiω,xn)≤Φ(Tiω)+θ0≤Φ(ω)+θ0，∀i≥M

d(Tjω，xn)≤Φ(Tjω)+θ0≤Φ(ω)+θ0,∀j≥M

由式(12)知，对上面的M, 存在i,j≥M满足

再由X一致凸且η单调及式(13)可得

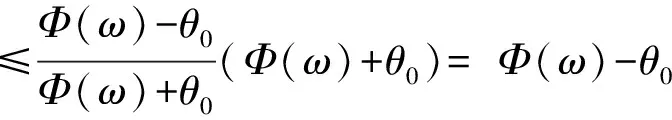
根据Φ的定义，我们有

根据T的定义有,

d(Tnω,Tω)≤and(Tn-1ω,ω)+bnd(Tn-1ω,Tω)

两端对n取极限有

d(ω,Tω)≤bd(ω,Tω)

由b<1可得Tω=ω.

参考文献：

[1] BROWDER F E. Semicontractive and semiaccretive nonlinear mappings in Banach spaces [J]. Bulletin of the American Mathematical Society, 1968, 74: 660-665.

[2] KOHLENBACH U. Some logical metaheorems with applications in functional analysis [J]. Transactions of the American Mathematical Society, 2005, 357(1): 89-128.

[3] KIRK W A. Krasnoselskii’s iteration process in hyperbolic Space [J]. Numerical Functional Analysis and Optimization, 1982, 4(4): 371-381.

[4] REICH S, SHAFRIR I. Nonexpansive Iterations in Hyperbolic Spaces [J].Nonlinear Analysis: Theory, Methods & Applications,1990, 15(6): 537-558.

[5] TAKAHASHI W. A Convexity in Metric Space and Nonexpansive Mappings [J].Kodai Mathematical Seminar Reports, 1970, 22(2): 129-250.

[6] LEUSTEAN L. A Quadratic Rate of Asymptotic Regularity for CAT (0) Spaces [J].Journal of Mathematical Analysis and Applications, 2007, 325(1): 386-399.