基于2种中介轴承的对转双转子系统耦合碰摩动力学模型

贾明明，关赛飞，秦海勤，于晓琳

（海军航空工程学院a.青岛校区，山东青岛266041；b.院务部，山东烟台264001）

基于2种中介轴承的对转双转子系统耦合碰摩动力学模型

贾明明a，关赛飞b，秦海勤a，于晓琳a

（海军航空工程学院a.青岛校区，山东青岛266041；b.院务部，山东烟台264001）

以2种不同支承形式的中介轴承双转子结构系统为研究对象，建立了对转双转子系统轴向—径向耦合碰摩有限元动力学模型。基于陀螺效应引起轮盘偏转产生轴向位移，导致轴向碰摩的假设，给出了轴向碰摩力与节点坐标之间的表达式，考虑了不同支承形式的中介轴承耦合力处理方式，并以此为基础详细推导了系统的振动微分方程。模型既能描述转静间的轴向碰摩和径向碰摩，又允许轴向碰摩和径向碰摩独立发生，亦可共同发生。

双转子；轴向碰摩；径向碰摩；反向旋转；中介轴承

对转双转子结构对于提高推重比、降低燃油消耗率等方面均大有益处[1-2]。为此，国内、外研究者对反向旋转双转子结构动力学特性进行了大量研究。如参考文献[3-5]重点研究了反向旋转双转子的临界转速特性和稳态不平衡响应特性。在此基础上，文献[6]进一步研究了外转子轴承不对中的反向旋转双转子系统振动响应。文献[7-8]对比研究了含滚动轴承的同向和反向旋转双转子系统的动力学响应和非线性响应。文献[9]则主要研究了刚度不对称反向旋转双转子系统的动力学特性。文献[10]设计了一个3级高性能的对转压气机，证明了对转结构对于发动机重量减轻、性能提高等具有很大优势。

对转结构虽然具有许多优点，但由于对转使得转子柔性变大，且现代航空发动机为提高性能转静子间隙越来越小，这些都导致对转双转子结构发生转静碰摩的可能性大大增加。而已有的文献[11-17]主要集中于同转双转子的碰摩，对于对转双转子的碰摩研究不是很充分。文献[18]设计了一种可模拟局部径向碰摩故障的对转双转子实验器，实验研究了对转双转子系统发生局部径向碰摩的振动特性，较好地揭示了反向旋转转静径向碰摩的故障现象。但对于实际的航空发动机转静子碰摩，不但可能发生径向碰摩，而且可能发生轴向碰摩[19-20]，如飞机空中大机动飞行时，由于陀螺效应的影响会引起盘的转动产生轴向位移，当该轴向位移超过转静间的初始轴向间隙时就会导致轴向碰摩的发生。轴向和径向碰摩发生时两者之间往往存在一定的耦合。文献[19-20]较好地描述和研究了双盘单转子系统的动力学特性。但对于对转双转子系统轴向—径向碰摩的研究报道并不多见。

本文在前人的研究基础之上，结合2种不同支承形式的中介轴承双转子结构特点，建立了一种正反旋转双转子系统轴向—径向复合碰摩力学模型，并以此为基础详细推导了碰摩力与节点坐标之间的表达式、不同中介轴承耦合力的处理方式及振动微分方程。

1 对转双转子系统动力学模型

1.1 双转子系统结构模型

图1和图2为本文所研究的双转子系统结构系统模型。图1和图2中双转子系统的低压转子（内转子）均支承在1号、2号、4号和5号轴承上，支承的形式为1-1-1型。1号和4号轮盘安装在低压转子轴上，1号轮盘位于1号和2号轴承间，4号轮盘位于4号和5号轴承间。高压转子均支承在3号和4号轴承上，支承形式为1-0-1型。2号和3号轮盘安装在高压转子轴上，且两轮盘都位于3号和4号轴承间。4号轴承均为高低转子的中介轴承。2系统的区别除外转子的长度和内外径不同外，主要在于4号轴承的支承形式不同。图1所示的结构I采用的是高压转子支承于滚动轴承外圈，低压转子支承于滚动轴承内圈的支承形式。图2所示的结构II采用的是高压转子支承于滚动轴承内圈，低压转子借助于4号盘支承于滚动轴承外圈的支承形式。在上述2模型中，既允许内外转子同向旋转也允许2转子反向旋转。

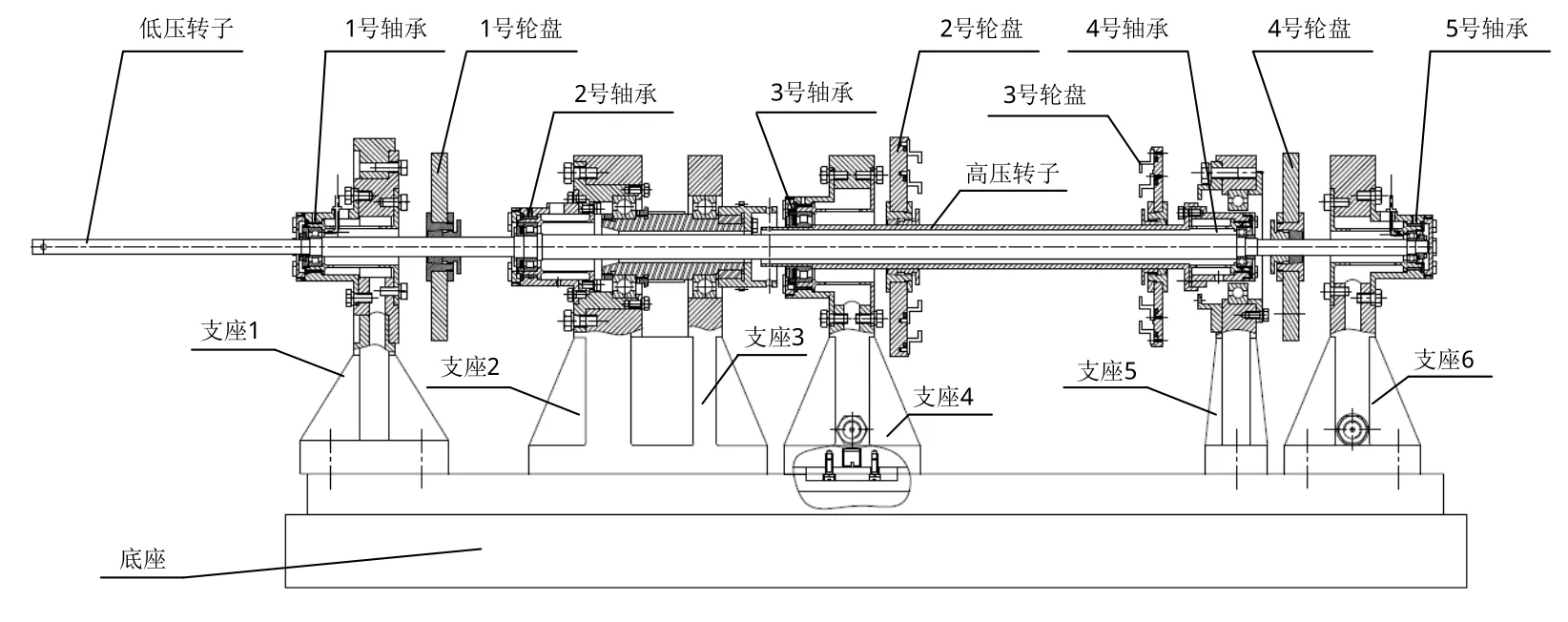
图1 结构Ⅰ型双转子系统模型Fig.1 Structure I dual-rotor system model

图2 结构Ⅰ型双转子系统模型Fig.2 Structure II dual-rotor system model

1.2 对转双转子系统有限元离散化模型

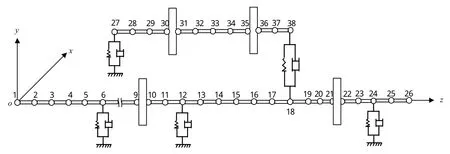
图3 结构Ⅰ型有限元模型Fig.3 Finite element discretization model of structure I

图4 结构Ⅰ型有限元模型Fig.4 Finite element discretization model of structure II

在结构I和结构II中，低压转子均离散化为26个节点，共25段。1号、3号、5号轴承分别位于节点6、12和24处。1号、4号轮盘分别等效为轴段9和轴段21。高压转子均离散化为12个节点，共11段。2号和4号轴承分别位于节点27和节点38处。2号、3号轮盘均等效为轴段30和轴段35。由于2系统的区别主要在于中介轴承的支承形式不同，因而离散化时根据其不同的支承形式，对结构I将4号中介轴承置于节点18和节点38间，对结构II将其置于节点31和节点38间。最终离散化的2系统轴段参数见表1和表2。

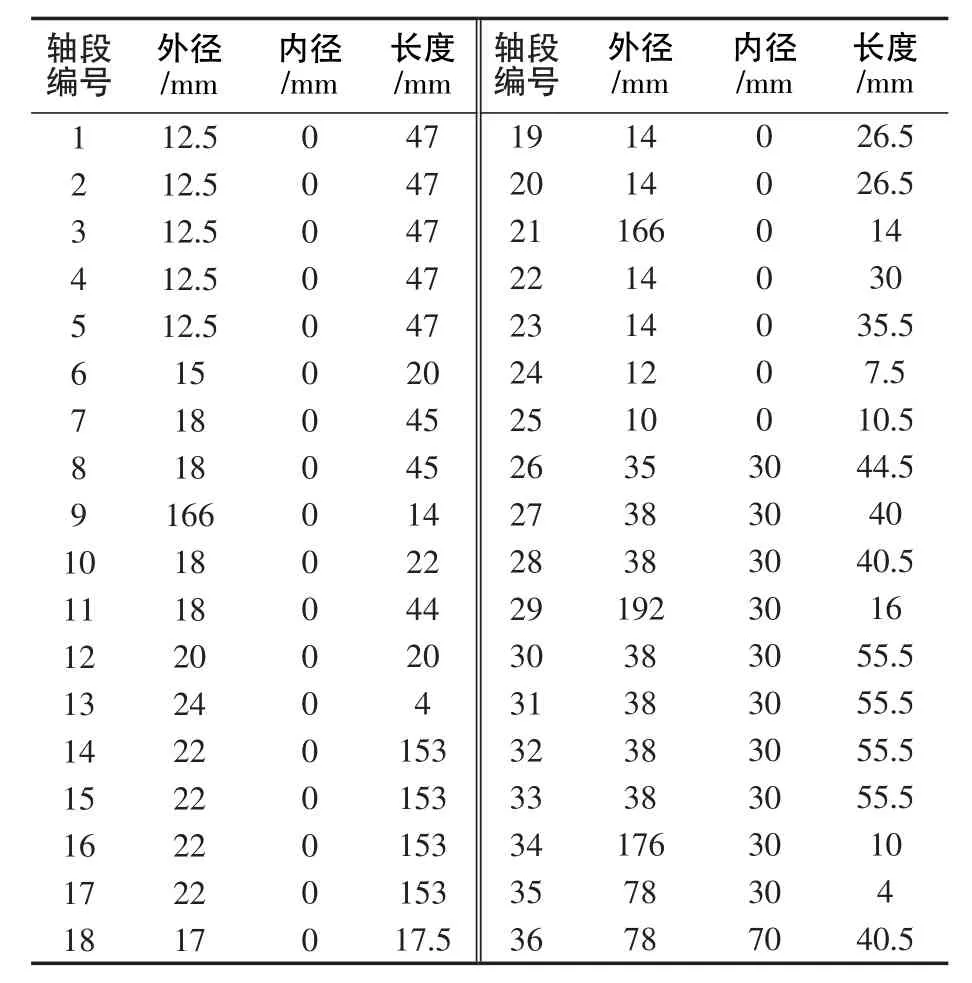
表1 结构Ⅰ轴段离散化参数Tab.1 Parameters of discrete rotor shaft section of structure I

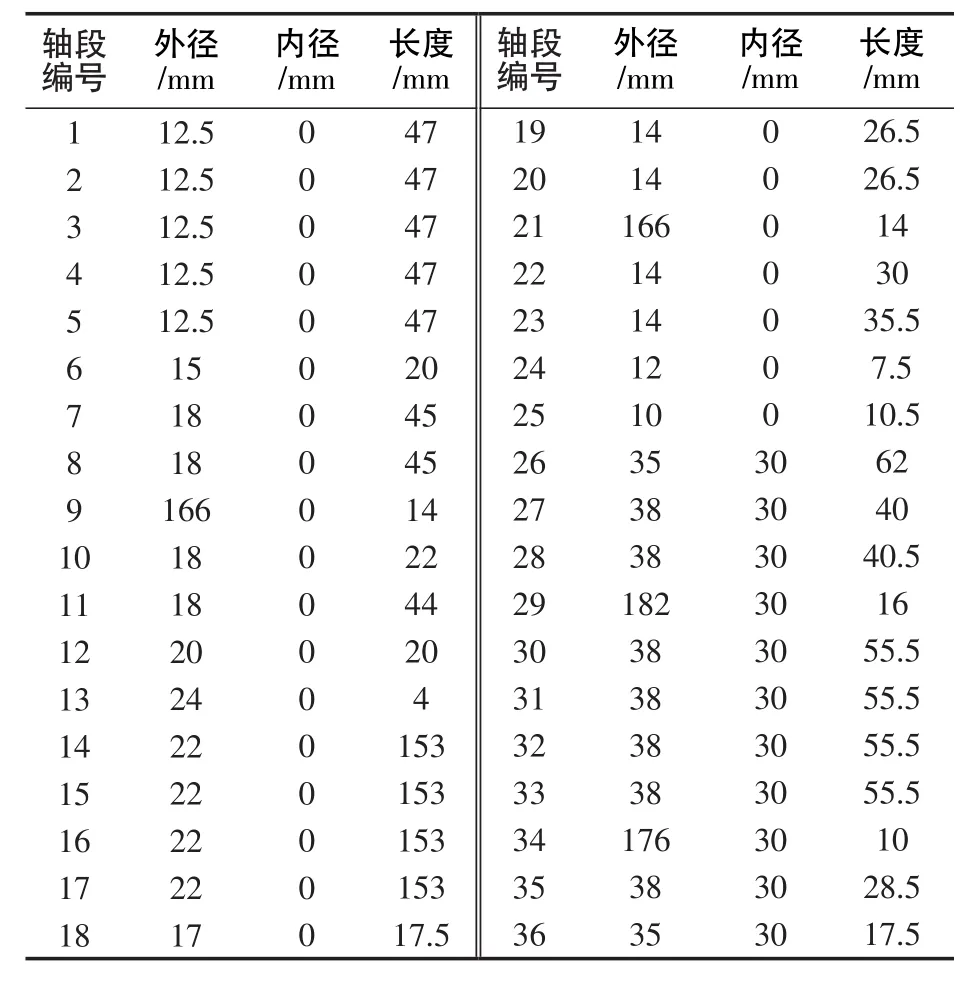
表2 结构Ⅰ轴段离散化参数Tab.2 Parameters of discrete rotor shaft section of structure II

由离散化的转子轴段参数，根据相应的表达式即可得单元的质量矩阵（包括平动和转动）、刚度矩阵和陀螺效应矩阵。对单元矩阵进行组合即可得到系统总体质量矩阵、总体刚度矩阵和总体陀螺效应矩阵[22]。

2 对转双转子系统碰摩动力学模型

2.1 对转双转子系统局部轴向碰摩力学模型

当转子系统工作时，轮盘所在的轴处会产生一定的挠度，该挠曲线是一空间曲线。由于陀螺效应的影响，导致轮盘相对于其原截面产生一定的偏转角θ和一定的轴向位移，局部轴向碰摩力模型如图5所示。实际的偏转角θ微小，根据微小角度矢量合成原则，可求得轮盘等效轴段2端的偏转角大小为（设内转子沿z轴方向第1个轮等效轴段2端节点编号为i和i+1，第2个轮盘等效轴段2端节点编号为j和j+1，外转子沿z轴方向第1个轮等效轴段2端节点编号为k和k+1，第2个轮盘等效轴段两端节点编号为l和l+1）：

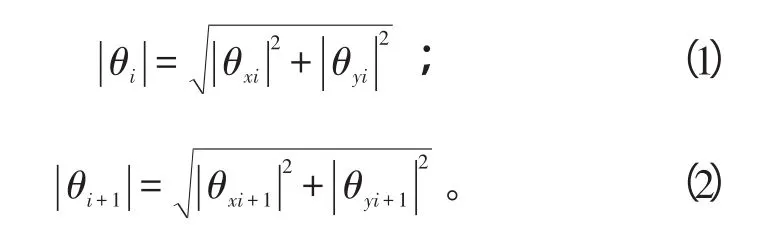
式（1）、（2）中：θxi和θyi分别是盘绕x轴和y轴的转角。由于θxi和θyi是在轴上2轮盘共同作用且内外轴相互影响作用下盘的x方向和y方向的转角，因而θi既包括了2轮盘的影响，又包括了内外轴的相互作用。

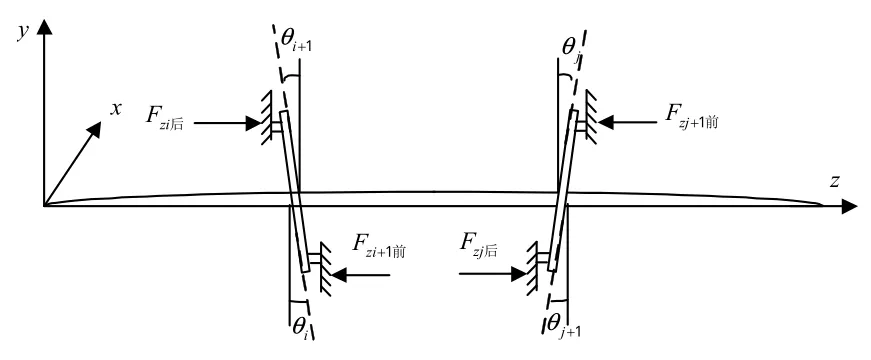
图5 局部轴向碰摩力模型Fig.5 Model of partial axial rubbing force

对于轮盘等效轴段其他端点的分析与此类似，下面以内转子第1轮盘为例进行说明。

假设可能发生碰摩的地方为轮盘上半径为r的点处，根据偏转角即可得到如图6所示的轮盘前、后碰摩点Ai和Ai+1的分布。

2碰摩点处的相对速度为：

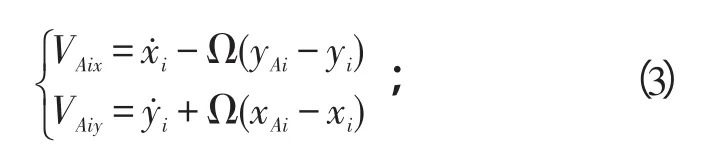
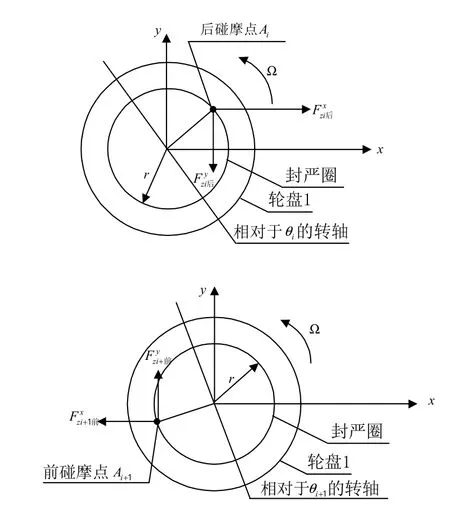
图6 局部轴向碰摩点分布Fig.6 Model of distribution of rubbing point

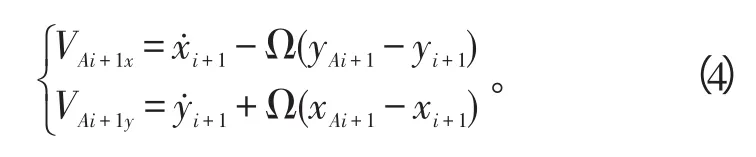
同理可得到内转子第2个盘的2碰摩点Bj和Bj+1处的相对速度：

图 12：ht t p://img.mp.itc.cn/upl oad/20170701/9163525ddcac 45349232f 91671978e27_t h.j pg

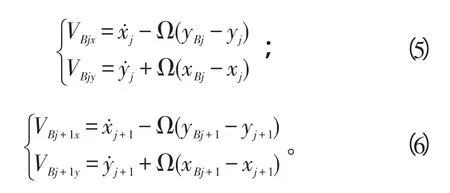
假定局部轴向碰摩属于干摩擦，不计摩擦生热的影响，则由干摩擦力的相关理论推得碰摩点处的摩擦力为[19-20]

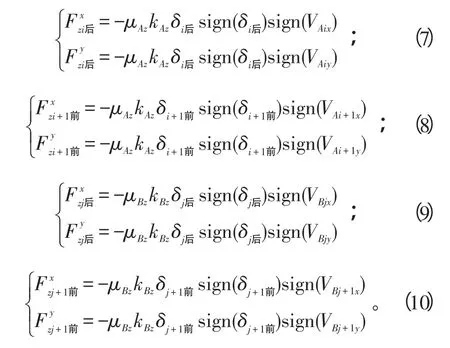
式（7）～（10）中：μAz、μBz分别为内转子2轮盘的轴向摩擦系数；kAz、kBz分别为2轮盘的轴向摩擦刚度系统；δi后、δi+1前、δj后、δj+1前分别为2盘前、后的相对轴向间隙，δi后=rθi-Δi后，δi+1前=rθi-Δi+1前，δj后=rθj-Δj后，δj+1前=rθj-Δj+1前；sign(·)为符号函数；Δi后、Δi+1前、Δj后、Δj+1前分别为2盘前、后的初始轴向间隙。

进一步将轴向碰摩力表示为整体坐标下的轴向碰摩力矢量：

2.2 对转双转子系统局部径向碰摩力学模型

对于转静间的局部径向碰摩模型取简单的线弹性碰摩力模型，如图7所示。

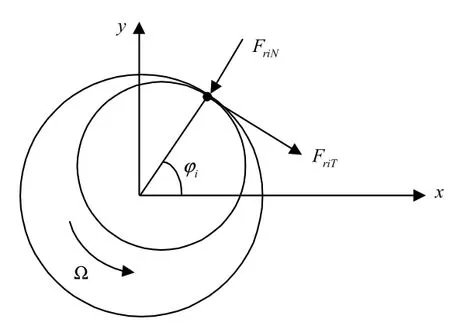
图7 径向局部碰摩模型Fig.7 Model of partial radial rubbing force

不考虑摩擦的热效应。依据该模型可得（以内转子第1个盘为例进行说明）：

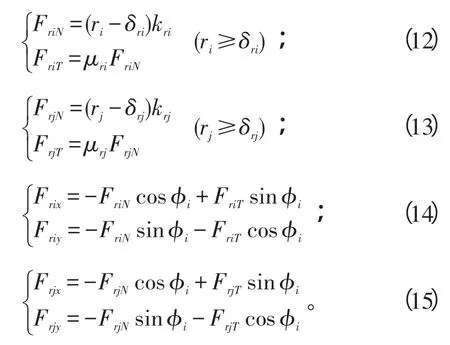
式（12）、（15）中：ri、rj为内转子第1个和第2个盘相对于静子机匣的径向位移，δi和δj分别为2盘与静子间的初始径向间隙；kri和krj为2盘的径向碰摩刚度系数；μri和μrj为2盘与静子间的径向摩擦系数。

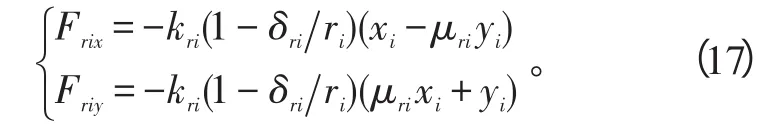
内转子第2个盘和外转子两盘的径向碰摩力表达式类同。进一步将径向碰摩力表示为整体坐标下的径向碰摩力矢量。

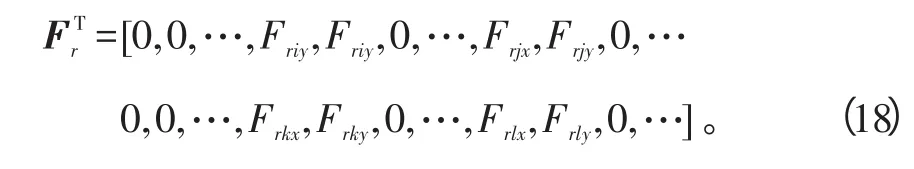
2.3 中介轴承耦合力学模型

对于航空发动机这一类同心轴的双转子系统，内转子轴和外转子轴往往通过中介轴承相互连接和支承。就作用力而言，对其中的任一转子轴，中介轴承和其他轴承并无本质区别。所不同的只是由于内外转子的相互影响，中介轴承作用力表达式更为复杂。为简化计算，不妨设中介轴承各向同性，且各向无相互影响，对应的内外转子轴节点编号分别为n和m。对于图3所示的中介轴承的支承形式，由于外转子（高压转子）支承于轴承外圈转速较高，工作时在离心力的作用下，外转子具有往外甩的趋势，容易打滑，故假设2转子具有如图8所示的耦合力。对于图4所示的中介轴承，由于外转子支承于轴承内圈，在离心力的作用下，外转子对内转子具有一定的抵紧作用，不易打滑，故假设2转子具有如图9所示的耦合力。

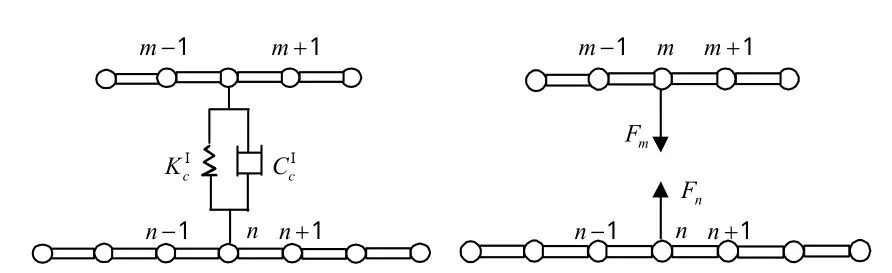
图8 结构Ⅰ型中介轴承耦合力学模型Fig.8 Coupling mechanics model of inter-shaft bearing in structure I

图9 结构Ⅰ型中介轴承耦合力学模型Fig.9 Coupling mechanics model of inter-shaft bearing in structure II

2种结构支承形式不同，耦合力方向也不相同。但对任一种支承形式，作用在节点n和m的耦合力向量Fn和Fm大小相等，方向相反。

以结构I为例进行说明，其Fn为：

则进一步将中介轴承耦合力表示为整体坐标下的耦合力矢量：

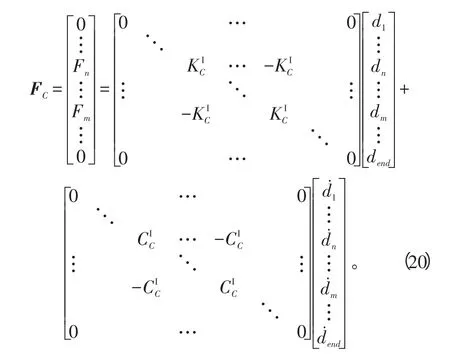
结构II的中介轴承耦合力类同，只是方向相反。

3 正反转双转子系统有限元振动微分方程

根据所建立的各模型，得到整个转子系统的受迫振动微分方程为[23]

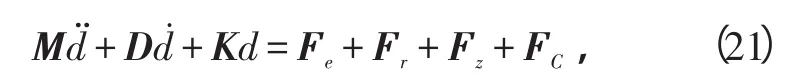
式中：M为系统集中质量矩阵；D为系统集中阻尼矩阵；K为系统集中刚度矩阵；Fe为不平衡力矢量；Fr为径向碰摩力矢量；Fz为轴向碰摩力矢量；FC为中介轴承耦合力矢量。

质量矩阵包括平动的质量矩阵和转动的质量矩阵，阻尼矩阵包括系统的黏性阻尼矩阵和陀螺矩阵。对于黏性阻尼，本文取Rayleigh阻尼即αM+βK，其中α、β是与系统前2阶阻尼系数和前2阶固有频率有关的常数。

不平衡力矢量Fe的表达式为

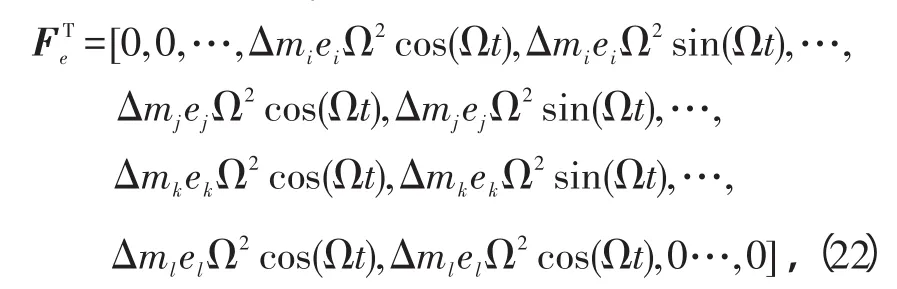
式中：Δmi、Δmj、Δmk、Δml分别为内外转子相应各轮盘的偏心质量；ei、ej、ek、el为内外转子相应各轮盘的偏心距。

4 小结

针对实际的正反旋转双转子系统，既可能发生径向碰摩也可能发生轴向碰摩或者2者相互耦合的现实问题，以2种不同支承方式的中介轴承双转子结构系统为研究对象，采用转子动力学有限元方法建立了正反旋转双转子系统轴向—径向复合碰摩力学模型。基于陀螺效应引起轮盘偏转产生轴向位移，导致轴向碰摩的假设，给出了轴向碰摩力与节点坐标之间的表达式。针对2种不同的中介轴承支承形式，考虑了不同的轴承耦合力处理方式。

所建立的模型能够描述转静间的轴向碰摩和径向碰摩，且轴向碰摩和径向碰摩既可以独立发生，亦可共同发生。该模型为正反旋转双转子系统轴向—径向复合碰摩振动特性的数值仿真分析和实验研究奠定了基础。

需指出的是本文所建碰摩模型尚难以全面描述导致碰摩发生的其他因素，更为完善和复杂模型的建立，有待于今后研究工作的深入和发展。

[1]POLACSEK C，BARRIER R.Numerical simulation of counter-rotating fan aeroacoustics[C]//13th AIAA/CEAS Aeroacoustics Conference，and Exhibit.Ohnert Park，2007：3680-3691.

[2]RYOJIRO MINATO，TOYOHIKO OTA，KIYOSHI FUKUTOMI，et al.Development of counter rotating axial fan turbojet engine for supersonic unmanned plane[C]// 43th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Cincinnati，2007：5023-5028.

[3]FENG GUOQUAN，ZHOU BAIZHUO，LUO GUIHUO. Vibration characteristic investigation of counter-rotating dual-rotor in aero-engine[J].Transactions of Nanjing Universtity of Aeronautics&Astronautics，2012，27（1）：33-39.

[4]冯国全，张连祥，伊峰.反向旋转双转子发动机稳态不平衡响应分析[J].哈尔滨工业大学学报，1998，30：249-252. FENG GUOQUAN，ZHANG LIANXIANG，YI FENG. Stationary unbalance response analysis of a two-spool engine with counter rotating rotors[J].Journal of Harbin Institute of Technology，1998，30：249-252.（in Chinese）

[5]胡绚，罗贵火，高德平.反向旋转双转子稳态响应计算分析与试验[J].航空动力学报，2007，22（7）：1044-1049. HU XUAN，LUO GUIHUO，GAO DEPING.Numerical analysis and experiment of counter-rotating dual-rotor’s steady-state response[J].Journal of Aerospace Power，2007，22（7）：1044-1049.（in Chinese）

[6]冯国全，周柏卓，林丽晶，等.内外双转子系统支撑轴承不对中分析[J].振动与冲击，2012，31（7）：142-147. FENG GUOQUAN，ZHOU BAIZHUO，LIN LIJING，et al.Misalignment analysis for support bearing in an innerand-outer dual-rotor system[J].Journal of Vibration and Shock，2012，31（7）：142-147.（in Chinese）

[7]罗贵火，周海仑，王飞，等.含滚动轴承的同向和反向旋转双转子系统动力学响应[J].航空动力学报，2012，27（8）：1887-1894. LUO GUIHUO，ZHOU HAILUN，WANG FEI，et al.Dynamic response of co-rotating and counter-rotating dualrotor system supported on ball bearing[J].Journal of Aerospace Power，2012，27（8）：1887-1894.（in Chinese）

[8]罗贵火，胡绚，杨喜关.反向旋转双转子系统非线性分析[J].振动工程学报，2009，22（3）：268-273. LUO GUIHUO，HU XUAN，YANG XIGUAN.Nonlinear dynamic performance analysis of counter-rotating dual-rotor system[J].Journal of Vibration Engineering.2009，22（3）：268-273.（in Chinese）

[9]FERRARIS G，MAISOUNEAVE V，LATANNE M.Prediction of the dynamic behavior of non-symmetric coaxial co-or counter-rotating rotors[J].Journal of Sound and Vibration，1996，195（4）：649-666.

[10]JEFFREY H FREEDMAN.Design of a multi-spool，highspeed，counter-rotating，aspirated compressor[D].Cambridge：Massachusetts Institute of Technology，2000：199-218.

[11]TORKHANI M，MAY L，VOINIS P.Light，medium and heavy partial rubs during speed transients of rotating machines：Numerical simulation and exprimental observation [J].Mechanical Systems and Signal Processing，2012，29：45-66.

[12]PENNACCHI P，BACHSCHMID N，TANZI E.Light and shot arc rubs in rotating machines：experimental tests and modeling[J].Mechanical Systems and Signal Processing，2009，23：2205-2227.

[13]CHU FULEI，LU WENXIU.Stiffening effect of the rotor during the rotor-to-stator rub in a rotating machine[J]. Journal of Sound and Vibration，2007，308：758-766.

[14]CHU FULEI，LU WENXIU.Experimental observation of nonlinear vibrations in a rub-impact rotor system[J].Journal of Sound and Vibration，2005，283：621-643.

[15]AGNIESZKA MUSZYNSKA.Rotor dynamics[M].Nevada：CRC Press Taylor&Francis Group，2005：641-660.

[16]符娆，张群岩，赵述元.航空发动机转静子碰摩故障信号用小波分析的方法检测和分析[J].噪声与振动控制，2012（1）：124-127. FU RAO，ZHANG QUNYAN，ZHAO SHUYUAN.Detection and analysis of aero-engine rotor-stator rubbing trouble using wavelet analysis[J].Journal of Sound and Vibration，2012（1）：124-127.（in Chinese）

[17]陈果，李成刚，王德友.航空发动机转子—滚动轴承—支承—机匣耦合系统的碰摩故障非线性动力学响应分析[J].航空动力学报，2007，22（10）：1771-1778. CHEN GUO，LI CHENGGANG，WANG DEYOU.Nonlinear dynamic analysis and experiment verification of rubbing faults of rotor-ball bearing-support-stator coupling system for aero-engine[J].Journal of Aerospace Power，2007，22（10）：1771-1778.（in Chinese）

[18]王四季，廖明夫，蒋云帆，等.对转双转子局部碰摩故障实验[J].推进技术，2013，34（1）：31-36. WANG SIJI，LIAO MINGFU，JIANG YUNFAN，et al. Experimental study on local rub-impact fault of counterrotating dual-rotor[J].Journal of Propulsion Technology，2013，34（1）：31-36.（in Chinese）

[19]徐可君，秦海勤.一种考虑径向—轴向碰摩的双盘转子—机匣系统力学模型的建立[J].振动与冲击，2007，26（8）：17-21. XU KEJUN，QIN HAIQIN.Application of generalized demodulation time-frequency analysis method to the processing of modulated signals[J].Journal of Vibration and Shock，2007，26（8）：17-21.（in Chinese）

[20]徐可君，秦海勤.径向—轴向碰摩双盘转子—机匣系统的数值仿真分析[J].振动与冲击，2007，26（7）：74-79. XU KEJUN，QIN HAIQIN.Numerical simulation analysis for rubbing model of a two-disk rotor-stator system[J]. Journal of Vibration and Shock，2007，26（7）：74-79.（in Chinese）

[21]张娅，王维民，姚剑飞.双盘转子系统轴向—径向碰摩非线性动力学特性分析[J].振动与冲击，2012，31（12）：141-145. ZHANG YA，WANG WEIMIN，YAO JIANFEI.Nonlinear dynamic behavior of a double-disk isotropic rotor system with axial and radial rub-impacts[J].Journal of Vibration and Shock，2012，31（12）：141-145.（in Chinese）

[22]RAO J S.旋转机械动力学及其发展[M].叶洎沅，译.北京：机械工业出版社，2012：265-281. RAO J S.Dynamics of rotating machine and its development[M].YE JIYUAN，Translated.Beijing：Machinery Industry Press，2012：265-281.

[23]韩清凯，于涛，王德友，等.故障转子系统的非线性振动分析与诊断方法[M].北京：科学出版社，2010：40-49. HAN QINGKAI，YU TAO，WANG DEYOU，et al.The nonlinear vibration analysis of failure rotating system and diagnostic method[M].Beijing：Science Press，2010：40-49.（in Chinese）

Dynamics Model of Dual Rotor System Coupling Centact Based on Two Kinds of Intermediary Bearing

JIA Ming-minga,GUAN Sai-feib,QIN Hai-qina,YU Xiao-lina

（Naval Aeronautical and Astronautical university a.Qingdao Branch,Qingdao Shandong 266041,China; b.Department of General Affairs，Yantai Shandong 264001,China）

A new axial-radial coupling rubbing dynamincs model of the counter-rotating dual-rotor system is built with the study object of the dual-rotor system with two different inte-shaft bearings.Based on the assumption that the gyroscopic effect causes disk deflection which produces axial displacement and leads to axial rubbing,the expression between axial rubbing force and node coordinates could be given.According to the two different intermediary bearing forms,distinct treatment of bearing coupling force is considered.And vibration differential equation of the system is deduced in detail. The model can be used to describe the axial rubbing and radial rubbing between the stator and the rotor,and the axial rubbing and radial rubbing can occur independently or dependently.

dual-rotor;rubbing;counter-rotating;inter-shaft bearing

TH133.33；V231.96

A

2014-03-11；

2014-04-20

贾明明（1982-），男，讲师，博士生。

1673-1522（2014）03-0257-07

10.7682/j.issn.1673-1522.2014.03.013