一类不定复空间型中Lagrange子流形的Chen型不等式

张 攀，张 量，宋卫东

(安徽师范大学数学计算机科学学院，安徽芜湖 241000)

一类不定复空间型中Lagrange子流形的Chen型不等式

张 攀，张 量，宋卫东

(安徽师范大学数学计算机科学学院，安徽芜湖 241000)

利用Riemann不变量和 Riemann流形上的最优化方法得到一类不定复空间型中Lagrange子流形的Chen型不等式，并证明了等号成立时子流形一定为全测地的.

不定复空间型;Lagrange子流形;Chen型不等式;全测地

向量，在L中选取局部正交标架场}，使得=X.记RicL(X)义M上的Riemann不变量如下:

特别地，当k=2时，δk(M)=δM.此外，文献［11］给出了复空间型中Lagrange子流形的一个Chen型不等式;文献［12］证明了该Chen型不等式等号成立时当且仅当子流形是全测地的.

定理1 设Mn为(c)中Lagrange类空子流形，n≥4，则Riemann不变量δn(M)满足

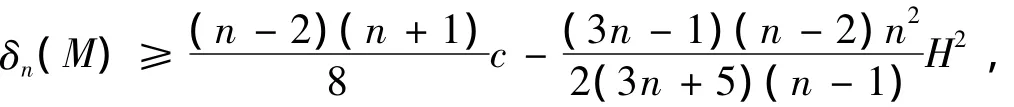
其中H为M的平均曲率.当等号成立时，Mn为全测地子流形.

1 预备知识

设Mn是Nnn/2(c)中实n维Lagrange类空子流形.在(c)上选取局部规范正交标架场:

使得其限制于Mn时，{e1，e2，…，en}与Mn相切.本文约定各类指标取值范围如下:

A，B，C，…=1，2，…，n，1*，2*，…，n*;i，j，k，…=1，2，…，n; α，β，γ，…=1*，2*，…，n*.设ωA为eA的对偶标架场，使得(c)的度量为εi=1;εα=-1.于是，(c)的结构方程为

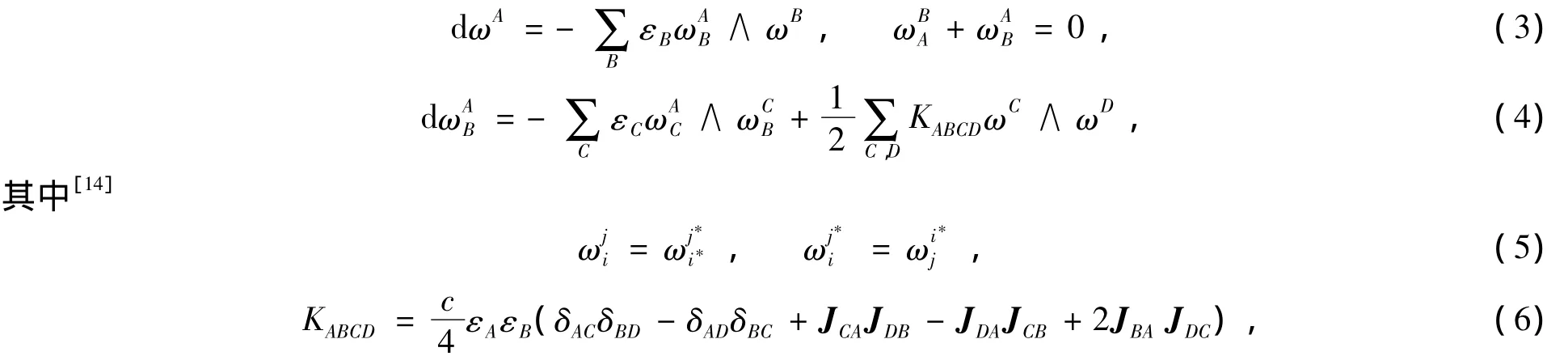
这里JAB为线性变换J关于{eA}的变换矩阵.

限制在Mn上，有

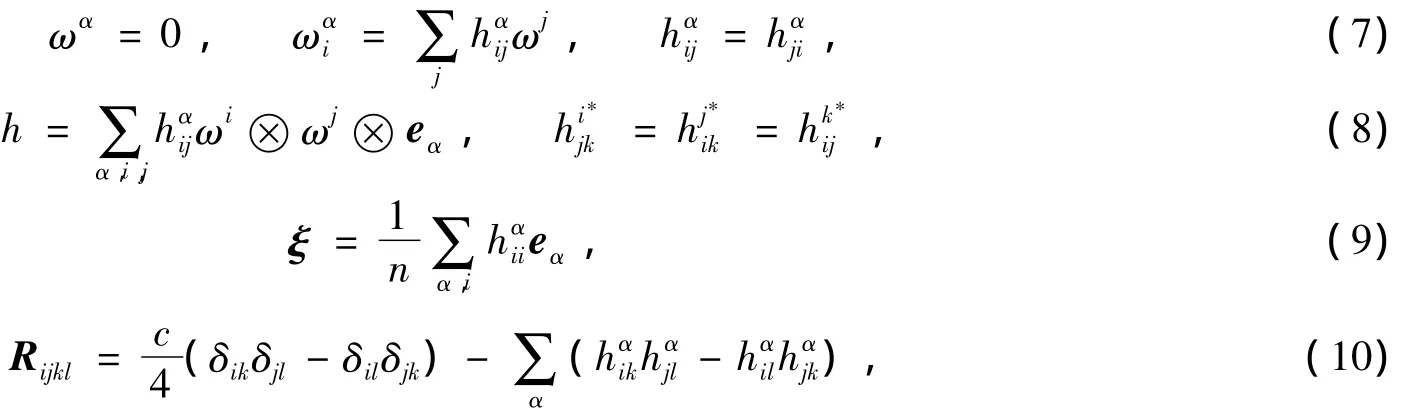
其中h，ξ，Rijkl分别是Mn的第二基本形式、平均曲率向量和曲率张量.定义H=‖ξ‖，Hα=()n×n.

设()为n维Riemann流形，M为N的m维子流形，N上的Riemann度量诱导了M上的Riemann度量g.设f:N→ℝ为可微函数.考虑条件极值问题:

可得:

引理1［6］假设x0∈M是问题(11)的解，则:

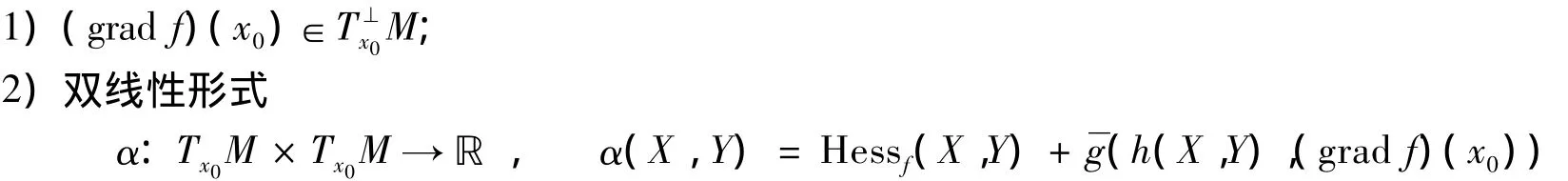
是半负定的，其中:gradf为函数f的梯度;h为M在N中的第二基本形式.

2 定理1中不等式的证明

对任意的x∈M，设单位切向量X∈TxM，且Mn在x点沿X方向的Ric曲率最小，在TxM和M中分别取标准正交基{e1，e2，…，en}和，…，}，使得e1=X.如果L=TxM，则由式(1)得

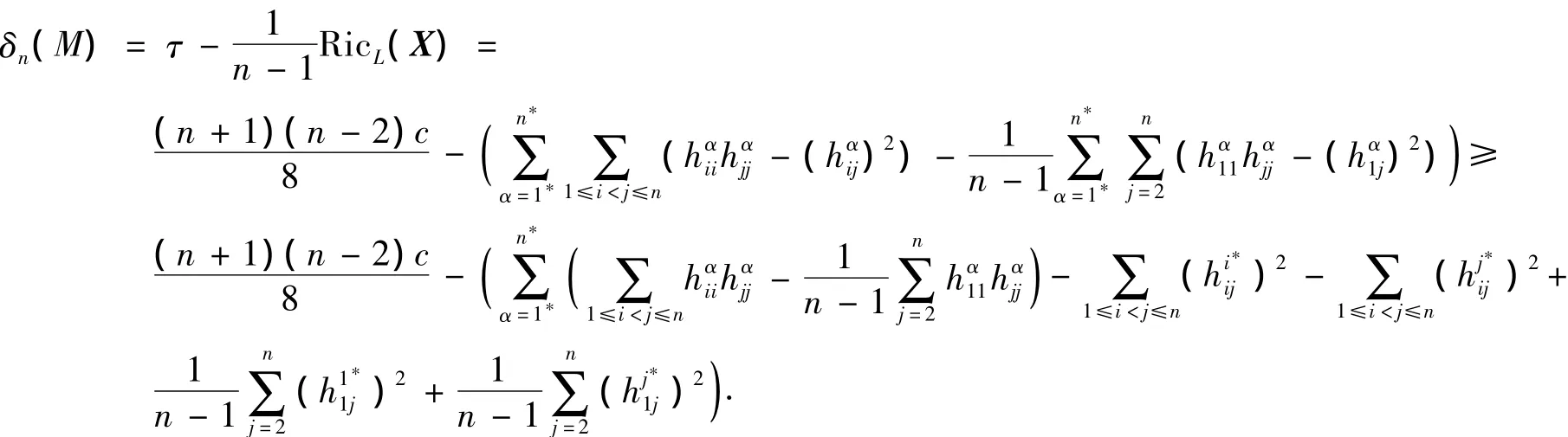
又由式(8)可得

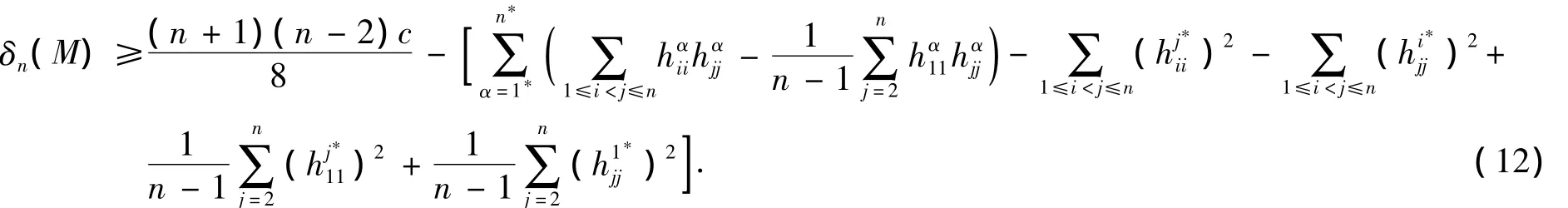
上，其中k1*为常数.对函数f1*关于每个自变量求偏导，有

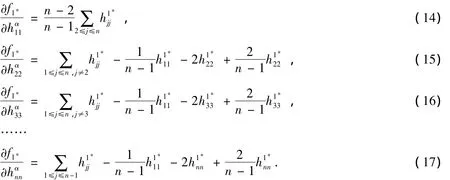
则由式(13)～(17)可得

设q为P上的任意一点，则双线性形式α:TqP×TqP→ℝ为

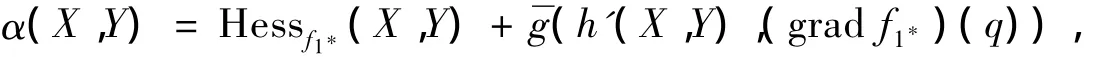
其中:h'为P上的第二基本形式;为ℝn上的Riemann度量.在ℝn的自然标架场下，的Hesse矩阵为

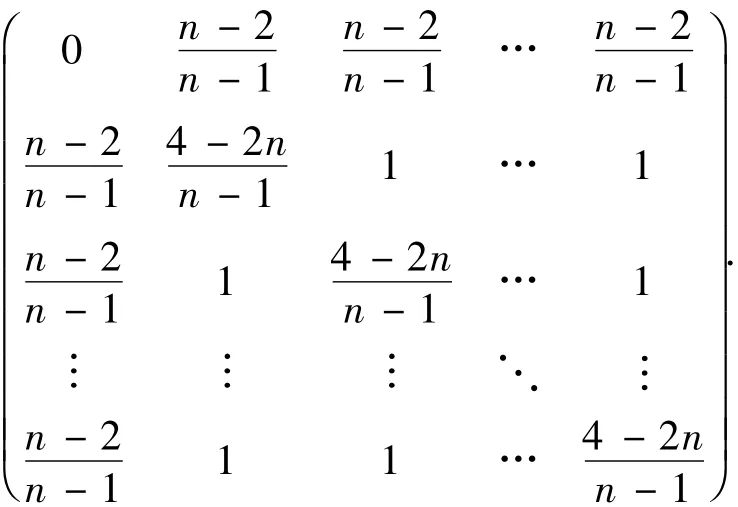
因为P为ℝn中的全测地子流形，考虑X∈TqP，易见

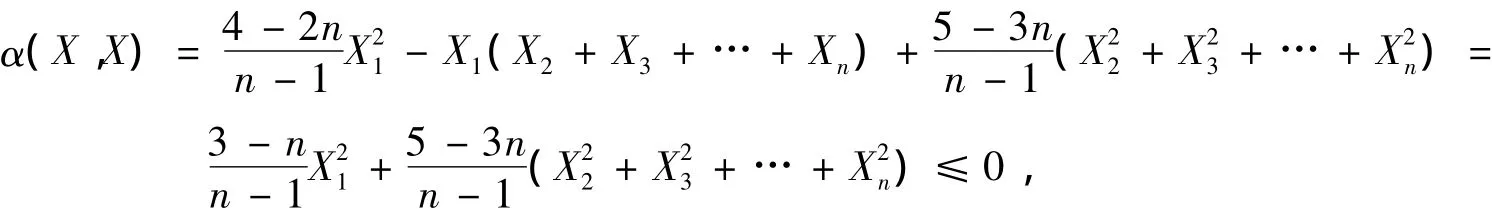
所以为凸函数，于是由式(18)给出的(，，…，)是最大值点，因此

考虑问题maxfα(α=2*，3*，…，n*)，限制在P:++…+=kα上，其中kα为常数.同理可得fα的(，…，hαnn)最大值点满足

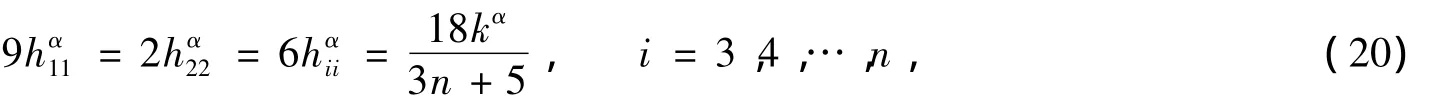
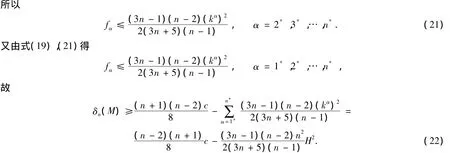
3 定理1中等号成立的证明

命题1 设Mn为(c)中Lagrange类空子流形，n≥3，x∈Mn，则δn(x)满足

当且仅当TxM中存在标准正交基{e1，e2，…，en}，使得

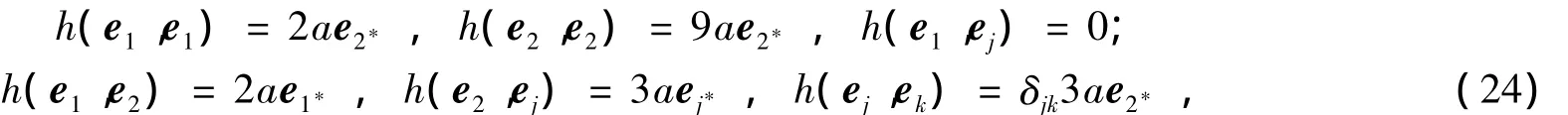
其中a为Mn上的函数，且j，k=3，4，…，n.

其中j，k=3，4，…，n且j≠k.

当等号成立时，注意到式(19)和式(21)，必有a1=0.在切空间TxM和法空间中分别取标准正交基{e1，e2，…，en}和，…，}，使得ξ=，再由式(8)可得式(24).证毕.

下面证明定理1中等号成立的结论.假设δn(x)满足式(23)，Mn不是全测地的，不妨假设在x点h(x)≠0.由命题1知，TxM中存在标准正交基{e1，e2，…，en}，使得式(24)成立.注意到h(x)≠0，则a≠0.因为与平均曲率向量平行，所以可以在x点的一个开邻域Ox将扩充为一个可微向量场，使得与平均曲率向量场平行.所以在开邻域Ox内任一点，Weingarten变换有3个特征值:2a，9a和3a，且重数分别为1，1，n-2.于是可将TxM的正交基{e1，e2，…，en}扩充为开邻域Ox的局部标准正交基，使得对Ox内任一点都有式(24)成立.

因为Mn为(c)的不变子流形［14］，所以对Mn上任意切向量场X，Y，Z，有

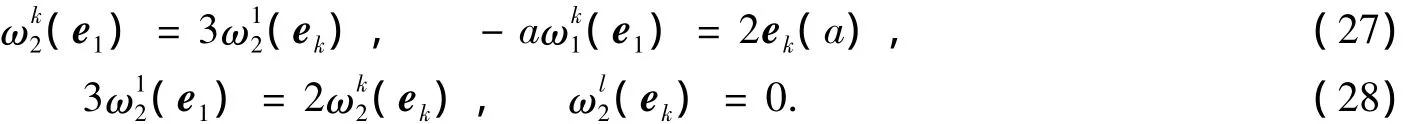
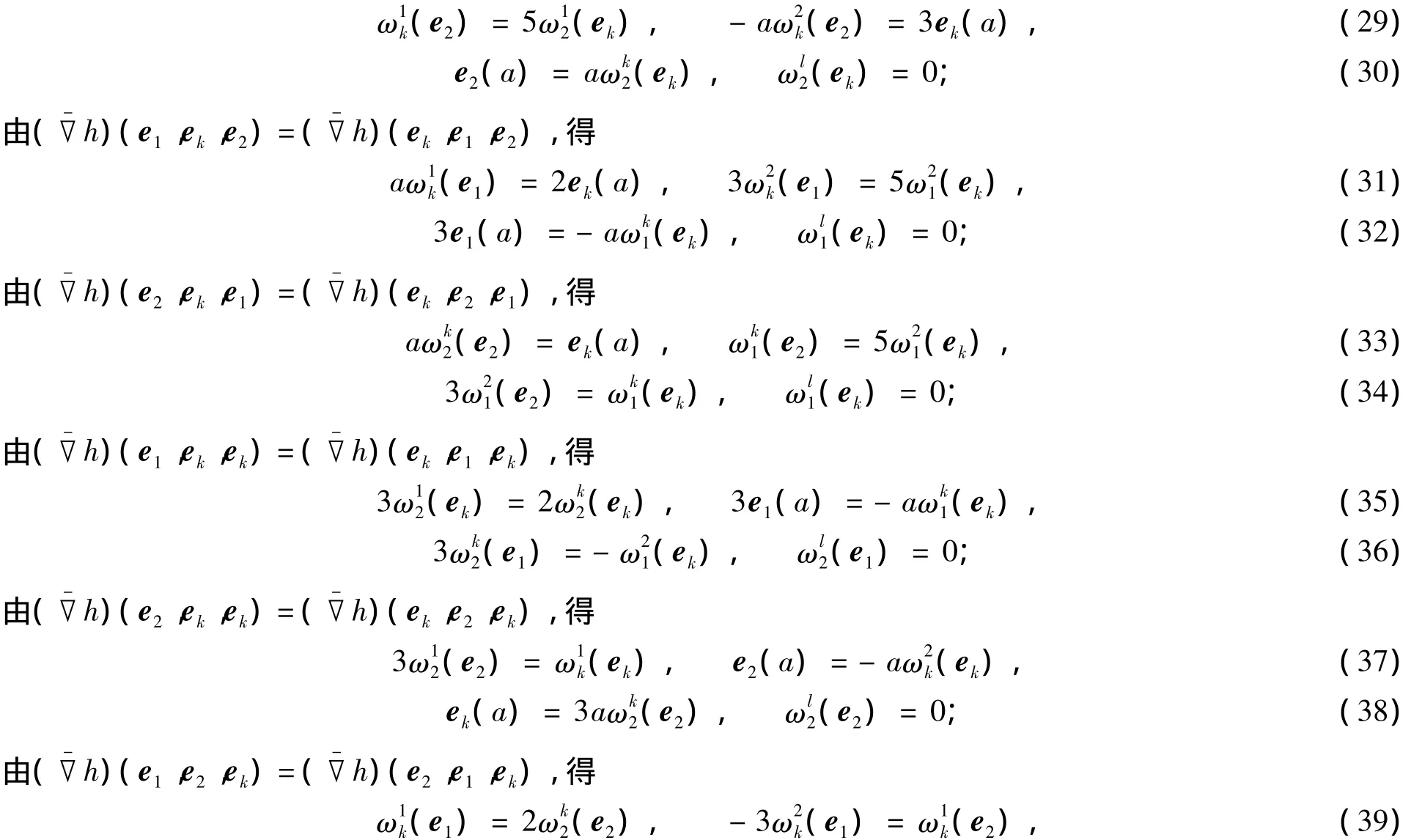
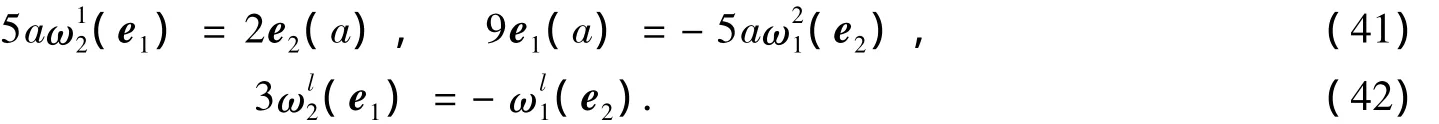
由式(29)，(33)可得ek(a)=0，再结合式(27)可得=0.由式(27)，(31)可得=0，再结合式(29)有=0.由式(40)，(41)有e1(a)=0，再结合式(32)有)=0.注意到式(34)，故有=0.由式(28)，(37)，(41)有)=0，再结合式(30)，(36)，(38)有=0.又由式(37)有

结合式(45)～(47)有a=0，这与a≠0的假设矛盾.故必有a=0，则Mn为全测地子流形.

［1］ CHEN Bangyen.Some Pinching and Classification Theorems for Minimal Submanifolds［J］.Arch Math，1993，60:568-578.

［2］ Chern S S.Minimal Submanifolds in a Riemannian Manifold［M］.Lawrence:University of Kansas Press，1968.

［3］ Chen B Y，Dillen F，Verstraelen L，et al.Totally Real Submanifolds of CPnSatisfying a Basic Equality［J］.Arch Math，1994，63(6):553-564.

［4］ Defever F，Mihai I，Verstraelen L.B.-Y.Chen’s Inequality for Submanifolds of Sasakian Space Forms［J］.Boll Unione Mat Ital，2001，4B(2):521-529.

［5］ Gülbahar M，Kilic E，Keles S.Chen-Like Inequalities on Lightlike Hypersurfaces of a Lorentzian Manifold［J］.Journal of Inequalities and Applications，2013，2013(1):266.

［6］ Oprea T.Optimizations Methods on Riemannian Submanifolds［J］.An Univ Buc，2005，1:127-136.

［7］ Oprea T.Chen’s Inequality in Lagrangian Case［J］.Colloq Math，2007，108:163-169.

［8］ Bolton J，Montealegre C R，Vrancken L.Characterizing Warped Product Lagrangian Immersions in Complex Projective Space［J］.Proc Edinb Math Soc，2009，52(2):273-286.

［9］ Tripathi M M.Improved Chen-Ricci Inequality for Curvature-Like Tensors and Its Applications［J］.Differential Geometry and Its Applications，2011，29(5):685-698.

［10］ CHEN Bangyen.Relations between Ricci Curvature and Shape Operator for Submanifolds with Arbitrary Codimensions［J］.Glasg Math J，1999，41(1):33-41.

［11］ Oprea T.On a Riemannian Invariant of Chen Type［J］.Rocky Mountain J Math，2008，38(2):567-581.

［12］ Dillen F，Fastenakel J.On an Inequality of Oprea for Lagrangian Submanifolds［J］.Cent Eur J Math，2009，7(1): 140-144.

［13］ CHEN Bangyen，Dillen F.Classification of Marginally Trapped Lagrangian Surfaces in Lorentzian Complex Space Forms［J］.Journal of Mathematical Physics，2007，48(1):013509.

［14］ CHEN Bangyen，Ogiue K.On Totally Real Submanifolds［J］.Trans AMS，1974，193:257-266.

(责任编辑:赵立芹)

Inequalities of Chen Type for Lagrangian Submanifolds of a Class of Indefinite Complex Space Form

ZHANG Pan，ZHANG Liang，SONG Weidong
(College of Mathematics and Computer Science，Anhui Normal University，Wuhu 241000，Anhui Province，China)

We obtained an inequality of Chen type for Lagrangian submanifolds of a class of indefinite complex space form using the Riemannian invariant and the optimization method on the Riemannian manifolds.In particular，we also showed that a Lagrangian submanifold of the indefinite complex space form attaining equality in the inequality must be totally geodesic.

indefinite complex space form;Lagrangian submanifolds;inequality of Chen type;totally geodesic

O186.12

A

1671-5489(2014)03-0439-06

10.13413/j.cnki.jdxblxb.2014.03.07

0 引言及主要结果

2013-07-15.

张 攀(1991—)，男，汉族，硕士研究生，从事微分几何的研究，E-mail:zhangpan1991622@sina.com.通信作者:张 量(1979—)，男，汉族，硕士，副教授，从事微分几何的研究，E-mail:zhliang43@sohu.com;宋卫东(1958—)，男，汉族，教授，从事微分几何的研究，E-mail:swd@sina.com.

安徽省高校优秀青年人才基金(批准号:2011SQRL021ZD).