结构方阵秩亏为k的可信性验证

李 喆，尹伟石，杨 华

(长春理工大学理学院，长春 130022)

结构方阵秩亏为k的可信性验证

李 喆，尹伟石，杨 华

(长春理工大学理学院，长春 130022)

利用区间算法研究结构矩阵秩亏为k的可信性验证.对具有特殊代数结构的矩阵A(p)，给出了算法输出具有相同代数结构的区间矩阵A(p+W)，其每个位置的元素为矩阵A(p)相应位置元素的很小区间摄动，使得区间矩阵A(p+W)中包含一个具有相同代数结构且秩亏为k的矩阵A(p+^w).结果表明，结构矩阵秩亏为k的可信性验证可以应用到多项式因式分解的可信性计算中.

区间算法;结构方阵;可信性验证;秩

1 预备知识

设ℝ表示实数集合，ℝ 表示实数区间.Om×n表示m×n零矩阵，In表示n×n单位矩阵.Mi，:和M:，i分别表示矩阵M的第i行和第i列.

命题1 设A∈ℝn×n，若对某个B，C∈ℝn×k，(n+k)×(n+k)矩阵

非奇异，则rank(A)=n-k当且仅当线性方程组

的解满足F=Ok×k.

证明:必要性.若 rank(A)=n-k，设 Nullspace(A)=span{b1，b2，…，bk}，则矩阵CT(b1b2… bk)非奇异，且存在唯一的矩阵B，使得CT(b1b2… bk)B=Ik.由于矩阵(1)非奇异，因此，线性方程组(2)的解为

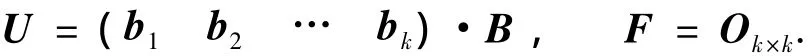
充分性.若F=Ok×k，则AU=On×k，CTU=Ik，故向量U:，1，U:，2，…，U:，k∈NullSpace(A)，且U:，1，U:，2，…，U:，k线性无关.若rank(A)＜n-k，不妨设Nullspace(A)=span{U:，1，U:，2，…，U:，k，a}，则必存在λ=(λ1，…，λk，λk+1)T∈ℝk+1，使得

这与矩阵(1)非奇异矛盾.故rank(A)=n-k.

命题2 设A∈ℝn×n且rank(A)=n-k.再设

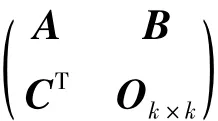
证明:只需证明

的解为U*=On×k，F*=Ok×k.将方程组

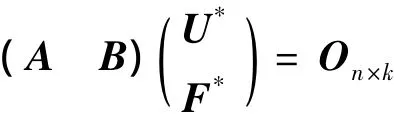
左乘矩阵(b1b2… bk)T，有

由(b1b2… bk)TB非奇异可知F*=Ok×k，故CTU*=Ok×k.进一步，由于AU*=On×k，故存在矩阵L，使得

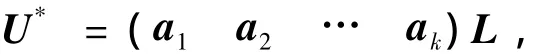
由CT(a1a2… ak)非奇异可知L=Ok×k，即U*=On×k.证毕.

文献［2］给出了系数阵为一般稠密矩阵的线性方程组求解的可信性验证方法，该算法已嵌入MATLAB中的INTLAB软件包，并命名为Verifylss函数.对于系数阵为区间矩阵的线性方程组，如果Verifylss函数输出一个区间向量，则该区间向量包含该区间线性方程组的所有可能解.

定理1［3］输入一区间矩阵A∈ ℝn×n及区间右端列向量b∈ ℝn，若Verifylss函数成功输出区间向量X⊂ℝn，则X满足条件

Moore［4］给出了非线性方程组解存在性的充分条件.在此基础上，Krawczyk［5］将牛顿迭代法应用于区间计算，以此验证非线性方程组的解.Rump［6］改善了区间牛顿迭代法，使其能更好地适用于实际应用.

定理2［6］设函数f:ℝn→ℝn，其中f=(f1，f2，…，fn)∈.给定初始近似解n，初始区间X∈ℝn，且0∈X.若存在区间矩阵M∈ℝn×n及实矩阵R∈ℝn×n满足下列两个条件:

定理3［7-8］设函数f:ℝm→ℝn构成零维多项式系统，其中f=(f1，f2，…，fn)∈C1，m＜n.如果存在非空的Zariski开子集A⊂Cm×n，使得对每个A∈A，都为方程A·f(x)=0的根，则在概率为1的情况下，为f(x)=0的根.

注1 设f:ℝm→ℝn(m＜n)，A∈ℝm×n为随机满秩矩阵.可通过验证方程A·f(x)=0的根验证方程f(x)=0的根.若存在区间X使得其含有A·f(x)=0的根，则在概率1的情况下，X含有f(x)=0的根.在实际应用中，采取计算f(X)做补充验证.若f(X)是一个非常小的包含0的区间，则在概率1的情况下，X含有f(x)=0的根［8］.

2 算 法

定义1 设A∈ℝn×n，给定数值秩容差ε∈ℝ.若A的奇异值σ1(A)，σ2(A)，…，σn(A)满足条件则称A的数值秩为n-k.

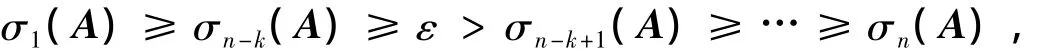
问题1 给定具有某一特殊代数结构的矩阵A(p)∈ℝn×n，其中p=(p1，p2，…，pl)T表示结构矩阵的参数.设矩阵A(p)的数值秩为n-r.如何确定参数扰动区间向量W=(W1，W2，…，Wl)T∈ ℝl，使得必存在实扰动∈W1∈W2，…∈Wl满足矩阵A(p+)秩亏为k，其中=，…，)T.

由命题1可得:

引理1 设A(p)∈ℝn×n为具有某一特殊代数结构的矩阵，其中p∈ℝl.设非线性函数

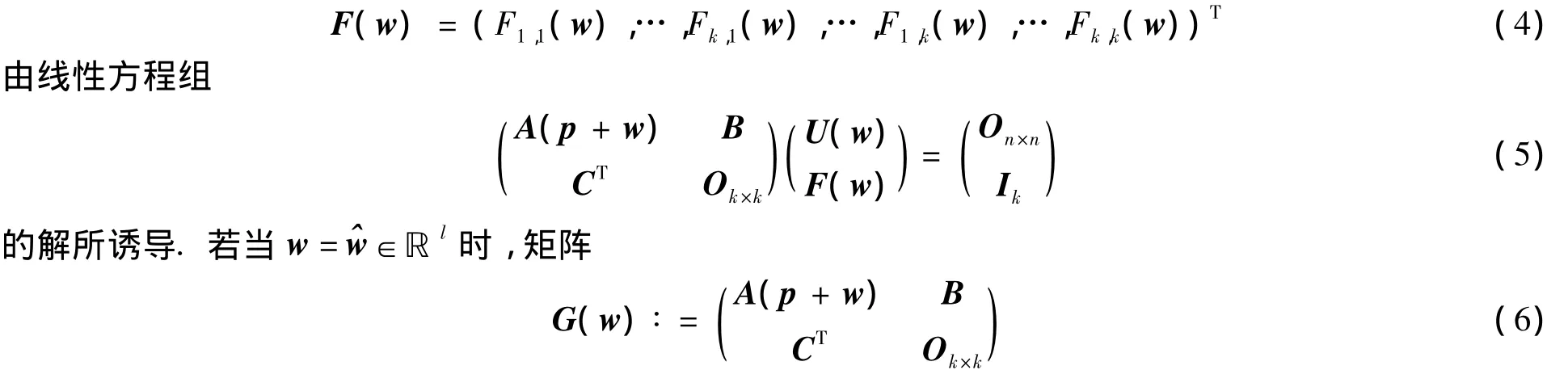
本文假设k2≤l，即假设非线性方程组F(w)=0为欠定方程组.结构矩阵奇异性的可信性验证依赖于初值=，…)的选取.先用文献［9］的数值方法得到优化的初值.设边界矩阵(6)当w=时非奇异，假设为F(w)=0的近似解，计算在w=附近F(w)=0的可信解.

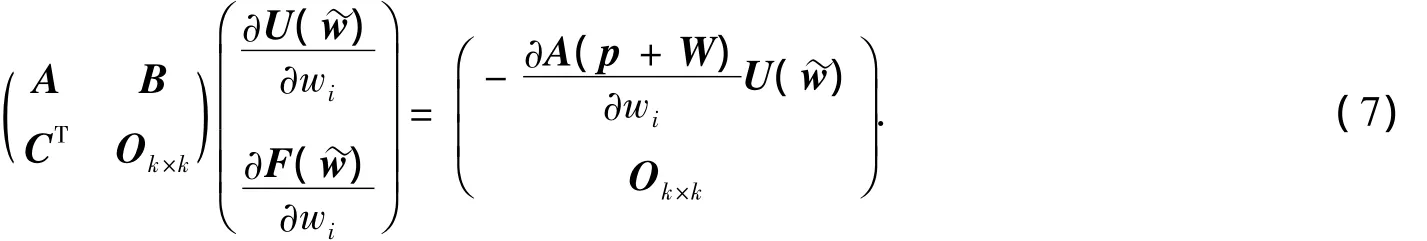
求解线性方程组(7)，可计算F(w)=0的Jacobi矩阵JF()［10］.设JF()的数值秩为r，选取指标集i1，i2，…，ir，使得数值列满秩，其中表示由矩阵JF()的第i1，i2，…，ir列所构成的矩阵.令

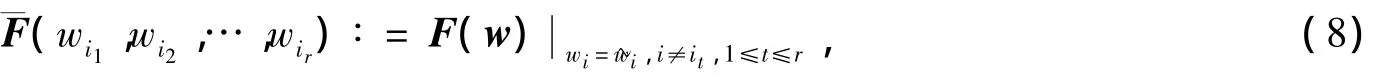
令Wit∈ ℝ且0∈Wit，1≤t≤r.设 R为矩阵 H·J¯F(，…，)的近似逆矩阵.令=+，1≤t≤r.利用MATLAB中Verifylss函数求解线性方程组(5)，得到区间矩阵U，使得U⊇U(++，…).进而，利用Verifylss函数，求解线性方程组(7)，得到区间矩阵J满足条件

令R为矩阵J¯F(~w)的近似逆矩阵，若

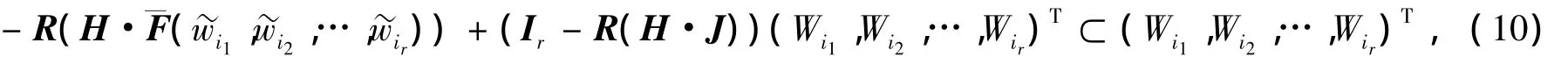
根据上述理论，设计算法如下.

算法1

输出:

步骤:

①令iter表示迭代次数，初始iter=1;初始区间向量∈ℝ且0∈，1≤t≤r;令Wi=0，i≠it，1≤t≤r;选取随机矩阵H∈，令R为区间矩阵H·J¯F(，…)近似逆矩阵;

②计算满足条件(9)的区间矩阵J，如果条件(10)成立，转步骤4);否则，令

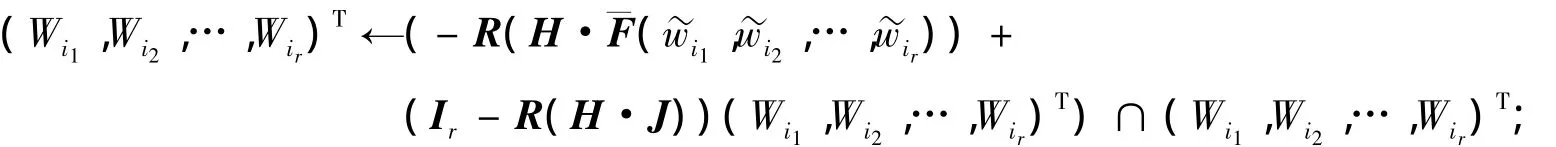
令iter←iter+1，返回步骤②;

③如果iter=T，则区间牛顿迭代法不收敛，返回“失败”，算法终止.

由引理1和定理3易证如下命题.

3 应用实例

给定对称矩阵

其中p=(0.98，2.01，2.99，4，6，9)T.令tol2=10-12.利用文献［9］方法可得数值初值:

1)计算JF(~w)的数值秩为r=2，选取指标值i1=1，i2=2.

2)令W1=［-10-12，10-12］，W2=［-10-12，10-12］，经计算条件(10)成立.

3)计算‖F(~w+W)‖＜10-12，则在概率为1的情况下，

［1］ 李喆，周蕊.结构方阵秩亏为1的可信性验证［J］.吉林大学学报:理学版，2013，51(6):1101-1103.(LI Zhe，ZHOU Rui.Certification of Square Structure Matrix with Rank Deficiency One［J］.Journal of Jilin University:Science Edition，2013，51(6):1101-1103.)

［2］ Rump S M.Kleine Fehlerschranken Bei Matrixproblemen［D］.Karlsruhe:University Karlsruhe，1980.

［3］ Rump S M.Verification Methods:Rigorous Results Using Floating-Point Arithmetic［J］.Acta Numerica，2010，19: 287-449.

［4］ Moore R E.A Test for Existence of Solutions to Nonlinear System［J］.SIAM J Numer Anal，1977，14(4):611-615.

［5］ Krawczyk R.Newton-Algorithmen zur Bestimmung von Nullstellen mit Fehlerschranken［J］.Computing，1969，4:187-201.

［6］ Rump S M.Solving Algebraic Problems with High Accuracy［C］//Proceeding of the Symposium on a New Approach to Scientific Computation.San Diego:Academic Press，1983:51-120.

［7］ Sommese A J，Wampler C WⅡ.The Numerical Solution of Systems of Polynomials Arising in Engineering and Science［M］.Singapore:World Scientific Publishing，2005.

［8］ YANG Zhengfeng，ZHI Lihong，ZHU Yijun.Verfied Error Bounds for Real Solutions of Positive-Dimensional Polynomial Systems［C］//ISSAC’13 Proceedings of the 38th International Symposium on International Symposium on Symbolic and Algebraic Computation.New York:ACM，2013:371-378.

［9］ Golub G H，Van Loan C F.Matrix Computations［M］.3rd ed.Baltimore:Johns Hopkins University Press，1996.

［10］ Spence A，Poulton C.Photonic Band Structure Calculations Using Nonlinear Eigenvalue Techniques［J］.J Comput Phy，2005，204(1):65-81.

(责任编辑:赵立芹)

Certification of the Square Structure Matrix with Rank Deficiency k

LI Zhe，YIN Weishi，YANG Hua
(College of Science，Changchun University of Science and Technology，Changchun 130022，China)

The authors mainly discussed the certification of the square structure matrix with rank deficiencyk. For a square structure matrix A(p)，we gave an algorithm which outputs an interval square matrix A(p+W) with the same algebraic structure such that A(p+W)contains a structure matrix A(p+^w)with rank deficiencyk，where each element of A(p+W)is a small interval perturbation of the corresponding element of A(p).

interval algorithm;square structure matrix;certification;rank

O241.3

A

1671-5489(2014)03-0465-05

10.13413/j.cnki.jdxblxb.2014.03.11

可信性验证也称为自验证方法，其研究目标是如何将浮点运算进行严格证明.对于给定的问题，利用可信性验证方法可以得出该问题的一个近似解及相应的误差界，使得在近似解的误差界范围内必存在一个精确解.令φ:ℝlℝn×n为参数p的线性矩阵函数，定义A(p)∶=φ(p)，则∶={A(p):p∈ℝl} 表示某类具有特殊代数结构的矩阵.本文推广文献［1］结构方阵秩亏为1的可信验证方法，给出了结构方阵秩亏为k的可信性验证方法.矩阵秩亏为k的可信性验证是指对于给定的矩阵，计算该矩阵中每个位置元素相应的区间扰动，以保证扰动后的区间矩阵中包含一秩亏为k的矩阵.结构方阵秩亏为k的可信性验证是指对于给定的、具有特殊代数结构的方阵A(p)，给出算法输出具有相同代数结构的区间方阵A(p+W)，其每个位置的元素为矩阵A(p)相应位置元素的很小区间摄动，使得A(p+W)中包含一个具有相同代数结构且秩亏为k的矩阵A(p+^w).结构矩阵秩亏为k的可信性验证可应用于多项式因式分解的可信性计算，而多项式因式分解的可信计算是符号与数值混合计算中的基本问题.本文利用边界矩阵理论，将验证结构矩阵秩亏为k的问题转化为计算一个由k×k个非线性方程构成的非线性方程组可信解.

2013-09-09.

李 喆(1981—)，女，汉族，博士，讲师，从事符号计算及符号数值混合计算的可信性计算研究，E-mail:zheli200809@ 163.com.通信作者:尹伟石(1980—)，男，汉族，博士，讲师，从事数学物理反问题的研究，E-mail:yinweishi@foxmail.com.

国家自然科学基金(批准号:11171133)和数学天元基金(批准号:11326209).