双相介质空间含有偏心裂纹的界面圆柱夹杂对SH波的散射
杨 杰
(上海电机学院 机械学院, 上海 200245)
双相介质空间含有偏心裂纹的界面圆柱夹杂对SH波的散射
杨 杰
(上海电机学院 机械学院, 上海 200245)
采用Green函数和“裂纹切割”方法,对全空间双相介质界面上含有偏心径向裂纹的圆柱形弹性夹杂,在入射SH波作用下的散射情况进行动应力分析。首先,构造所需的Green函数表达式;其次,采用“裂纹切割”方法及“界面契合”技术构造理论模型裂纹,然后,根据连续性条件建立第一类Fredholm积分方程组,考虑弱奇异积分方程组可以直接离散及散射波的衰减特性求解此方程组;最后,通过算例,分析裂纹长度、入射波数及介质参数等对裂纹尖端动应力强度因子的影响。
SH波; 偏心裂纹; 圆柱夹杂; 裂纹切割; 动应力强度因子
随着社会经济的快速发展,天然介质和工程材料被广泛地应用。然而,在这些介质中不可避免地存在各种各样的缺陷,例如不同的岩层结构或复合材料中孔洞、夹杂或裂纹的存在。考虑到含有介质缺陷的材料或结构在动态荷载的作用下所体现出的特殊性能,近年来研究人员越来越广泛地关注介质缺陷附近的动态响应问题[1-5]。
当介质中存在裂纹时,裂纹周围应力值很可能由于动荷载的作用而提高。1998年,鲍亦兴[6]就提出裂纹尖端动应力强度因子数值由于裂纹长度等因素的影响而相比静态情况时提高近30%。因而,有关裂纹缺陷的介质在弹性波作用下的研究更加引起研究人员的注意。2000年,陆建飞等[7]利用Cauchy型奇异方程的方法对弹性波入射情况下介质中同时含有圆形夹杂和曲线裂纹的问题进行了研究,并给出其解析解答。随后,刘殿魁等[8-12]利用复变函数以及Green函数方法对稳态入射SH波作用下介质中含有圆形孔洞或夹杂与裂纹同时存在时解析解问题进行了研究。2010年,Bostrom等[13]采用奇异积分方程方法以及弗洛凯理论,对SH波入射情况下含有周期性排列界面裂纹的层状各向异性板的解析解问题进行了研究。但上述文献所研究的裂纹多数是在均匀无限空间中,而对于双相介质界面上缺陷和裂纹同时存在的相关研究却很少见。
本文主要研究全空间双相介质界面上含有偏心径向裂纹的圆柱形弹性夹杂,在稳态入射SH波作用下的动态力学特性。其创新点主要在于Green函数方法的应用以及裂纹的构造,即构造自由界面上含有半圆形弹性夹杂的半空间,在点源函数作用下的位移函数表达式作为Green函数以及利用“裂纹切割”方法构造本文所需的裂纹,建立“契合”模型并建立定解积分方程组。最后,通过数值计算讨论偏心径向裂纹尖端动应力强度因子随裂纹长度以及介质参数的变化情况。
1 理论模型和控制方程
双相介质空间含有偏心径向裂纹的圆柱弹性夹杂在稳态SH波作用下的理论模型如图1所示。其中,SH波的入射角度为α1,圆柱夹杂的半径为R0,裂纹长度为A0=A2-A1,通过圆心O建立直角坐标系Oxy。

图1 理论模型Fig.1 Theoretical model
在极坐标系(r,θ,z)中,位移函数W在入射SH波作用下满足如下方程:
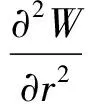
(1)
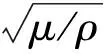

(2)
式中,τ为应力。在圆柱弹性夹杂周边和裂纹表面满足如下边界条件:
(3)
2 Green函数
采用Green函数模型如图2所示。即: 在一个含有半圆形弹性夹杂的半空间水平表面任意一点承受出平面点源载荷δ(r-r0)(其为时间谐和函数)时位移函数基本解答。
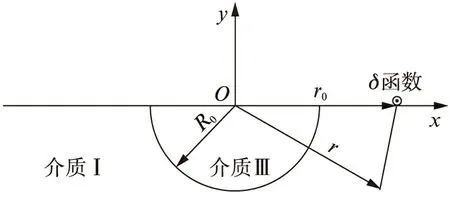
图2 Green函数模型Fig.2 Green function model
在极坐标系中,Green函数满足如下控制方程:
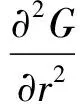
(4)
同时,其应力表达式由下式决定:
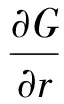
(5)
边界条件可以表示成:
(6)
3 构造裂纹和建立“契合”模型
稳态SH波入射时,介质中入射波为
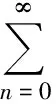
(7)

由于双相介质界面的存在,入射波将在界面处产生反射和折射,其相应的位移表达式为
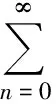
(8)
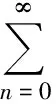
(9)
式中,W2、W3分别为反射波和折射波位移幅值;α2、α3分别为反射角度和折射角度;k2为介质Ⅱ中的波数,同时参数之间满足:


α2=-α1,cosα3=(c2/c1)cosα1
式中,c1、c2为介质Ⅰ和介质Ⅱ中SH波传播速度。
由于界面处存在圆柱形弹性夹杂,故入射波、反射波、折射波在其周边产生的散射波及其内部产生的驻波位移表达式分别为
(10)
(11)
(12)
(13)
(14)
(15)

同时,式(7)~(15)对应的应力表达式可通过式(2)求出。为了求解本文问题,采用“裂纹切割”方法构造裂纹,并建立“契合”模型如图3所示。

图3 “契合”模型Fig.3 Model of conjunction
在介质Ⅰ中,入射波、反射波在界面处产生的总位移和总应力分别为
W(11)=W(i)+W(is)+W(r)+W(rs),
(16)
|r|>R0
W(12)=W(it)+W(rt), |r| (17) (18) (19) 在介质Ⅱ中,折射波在界面处产生的总位移和总应力分别为 W(21)=W(f)+W(fs),|rr|>R0 (20) W(22)=W(ft), |r| (21) (22) (23) 根据界面处应力和位移连续性条件,可得: (24) (25) 联立式(24)和(25),可得含有未知外力系f1(r0,θ0) 的定解积分方程组: (26) (27) 式中,式(26)和式(27)式是含有弱奇异性的第一类Fredholm积分方程组,考虑散射波的衰减特性,采用直接离散的方法将上述方程转化为线性代数方程来求解。 在计算中,通常定义一个无量纲的动应力强度因子为 (28) 图4 当和时,K3随k1A0的变化Fig.4 Variation of K3 with k1A0 (, =1.0, 图5 当和时,K3随k1R0和A0/R0的变化Fig.5 Variation of K3 with k1R0 and A0/R0 图6 当和时,K3随k1R0和的变化Fig.6 Variation of K3 with k1R0 and (A0/R0=0.5, 图7 当时,K3随和的变化Fig.7 Variation of K3 with and (A0/R0=0.5, 采用Green函数和“裂纹切割”方法,对全空间双相介质界面上含有偏心径向裂纹的圆柱形弹性夹杂,在入射SH波作用下的散射情况进行动应力分析。通过算例分析得出裂纹长度的数值越小,动应力强度因子最大值相对入射波数出现的越晚,而不同的介质参数组合也会一定程度上影响动应力强度因子的震荡情况。因此,在相应问题的研究中应予以重视。 [1] Pao Y H.Elastic Waves in Solids[J].ASME Journal of Applied Mechanics,1983,50(4b): 1152-1164. [2] Golub M V,Zhang C Z,Wang Y S.SH-wave propagation and scatteing in periodically layered composites with a damaged layer[J].Journal of Sound and Vibration,2012,331(8): 1829-1843. [3] Lee W M,Chen J T.Scattering of flexural wave in a thin plate with multiple circular holes by using the multipole trefttz method[J].International Journal of Solids and Structures,2010,47(9): 1118-1129. [4] Chen J T,Lee J W,Shyu W S.SH-wave scattering by a semi-elliptical hill using a null-field boundary integral equation method and a hybrid method[J].Geophysical Journal International,2012,188(1): 177-194. [5] Golub M V,Zhang C,Wang Y S.SH-wave propagation and scatteing in periodically layered composites with a damaged layer[J].Journal of Sound and Vibration 2012,331(8): 1829-1843. [6] Pao Y H.Applied mechanics in science and engineering[J].Applied Mechanics Review,1998,51(2): 141-153. [7] 陆建飞,王建华,沈为平.曲线裂纹和反平面圆形夹杂相交问题[J].固体力学学报,2000,21(3): 205-210. [8] 史守峡,杨庆山,刘殿魁,等.SH波对圆形夹杂与裂纹的散射及其动应力集中[J].复合材料学报,2000,17(3): 107-112. [9] 李宏亮,刘殿魁.SH波作用下圆形夹杂与裂纹的相互作用[J].哈尔滨工程大学学报,2004,25(5): 618-623. [10] 刘殿魁,陈志刚.椭圆孔边裂纹对SH波的散射及其动应力强度因子[J].应用数学与力学,2004,25(9): 958-966. [11] 杜永军,赵启成,黄燕,等.裂纹对圆孔SH波散射与动应力集中系数的影响[J].哈尔滨工业大学学报,2005,37(8): 1077-1079. [12] 杨在林,闫培雷,刘殿魁.SH波对浅埋弹性圆柱及裂纹的散射与地震动[J].力学学报,2009,41(2): 229-234. [13] Bostrom A,Kvasha O.Elastic SH wave propagation in a layered anisotropic plate with periodic interface cracks: exact versus spring boundary conditions[J].Journal of Mechanics of Materials and Structures,2010,5(1): 67-78. [14] 张行.断裂力学中应力强度因子的解法[M].北京: 国防工业出版社,1992: 1-26. [15] Loeber J F,Sih G C. Diffraction of anti-plane shear waves by a finite crack[J].Journal of the Acoustical, Society of America,1968,44(1): 90-98. Scattering of SH Waves by Interface Cylindrical Inclusion with Eccentric Crack in Bi-material Space YANGJie (School of Mechanical Engineering, Shanghai Dianji University, Shanghai 200245, China) A dynamic stress analysis of cylindrical elastic inclusion with an eccentric radial crack at the bi-material interface in the whole space impacted by incident SH-waves is made using the Green function and crack cutting methods. First,the Green function expression is constructed. Secondly,The crack of the theoretical model is constructed using the crack cutting method and the interface conjunction technique. Then,the Fredholm integral equations of the first kind are established under the continuity condition. The equations are solved with the direct discrete method of integral equations and the attenuation characteristic of scattering waves. Finally, Distribution of the dynamic stress intensity factors at the tip of the crack is studied from the numerical results influenced by the length of the crack, incident wave numbers, the medium parameters, and so on. SH wave; eccentric crack; cylindrical inclusion; crack cutting; dynamic stress intensity factor (DSIF) 2014 - 09 - 13 国家自然科学基金项目资助(10972064);上海高校青年教师培养资助计划项目资助(14AZ14);上海电机学院重点学科资助项目(12xk501) 杨 杰(1985 - ),女,讲师,博士,主要研究方向为波动理论及应用,E-mail: yangj@sdju.edu.cn 2095 - 0020(2014)06 -0311 - 06 O 347.4;O 348 A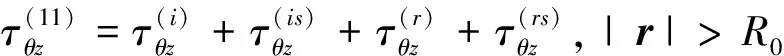









4 动应力强度因子(DSIF)

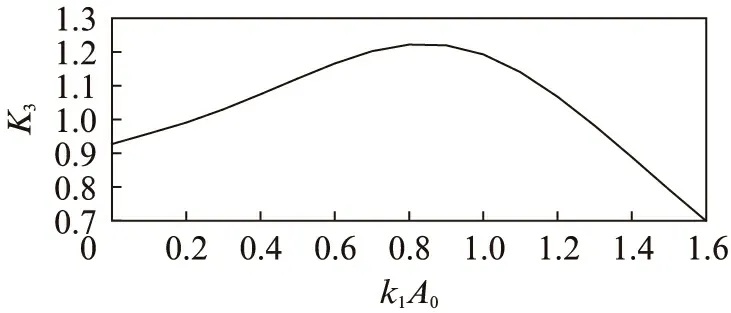
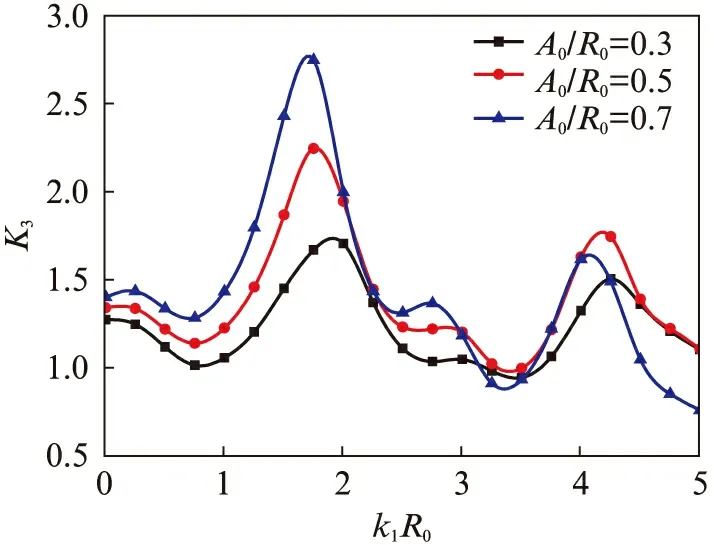
5 算例分析及讨论

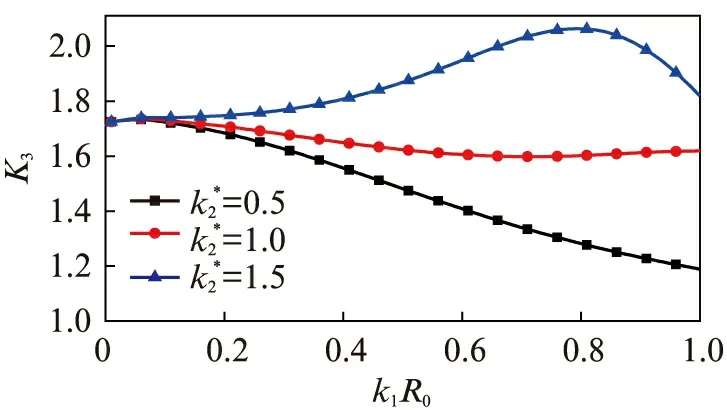


6 结 语

