改进Elman神经网络在氧化还原电位预测中的应用
蔡 鑫, 南新元 , 孔 军
(1.新疆大学 电气工程学院,新疆 乌鲁木齐 830047; 2. 江南大学 物联网工程学院,江苏 无锡 214122)
生物氧化提金受多种因素的影响和制约,是涉及热力学、动力学、生物化学、电化学的复杂的工业过程[1-3].在生物氧化预处理过程中,细菌的活性决定了金解析过程的效率,对整个体系的环境及其体系有关的各种操作因素都要有严格的要求.氧化还原电位反应了细菌氧化的进行情况,主要取决于Fe3+和Fe2+的比值[4].作为影响生物氧化体系的主要因素,对其预测在给料中黄铁矿含量的控制、生物氧化过程的稳定和优化、提金率都具有重要意义.氧化还原电位具有复杂的非线性影响,很难建立精确预测数学模型.而人工神经网络在处理复杂非线性问题上具有显著优势[5-6].为此,论文提出了一种基于遗传算法优化OHF Elman神经网络连接权值的GA-Elman模型,进行氧化还原电位预测.以新疆某金矿生物氧化提金过程中氧化还原电位的实测数据为例,并以GA-BP预测模型作为对比模型,实验结果表明该方法是可行的.
1 OHF Elman神经网络
1.1 网络模型
OHF Elman(ouput-hidden feedback Elman)即输出-隐层反馈Elman人工神经网络[7],这是在Elman网络的基础上所提出的一种改进的神经网络模型,结构如图1所示.该模型除了输入层、隐层、输出层单元外,还有一个特殊的联系单元,联系单元是用来记忆隐层单元以前时刻的输出值,可认为是一时延算子[8].因此这里前馈连接部分可以进行连接权值修正,而递归部分则是固定的,即不能进行学习修正.在Elman网络模型中只计入了隐层节点的反馈,而没有考虑输出层节点的反馈.由于各层神经元的反馈信息会影响网络的信号处理能力,因此在OHF Elman网络中增加了输出层节点的反馈,称之为联系单元2,并将它放在第2层,与隐层节点一起作为输出层的输入.

图1 OHF Elman神经网络结构图
其数学模型为
x(k)=f(W1xc(k)+W2u(k-1)),
(1)
xc(k)=α·xc(k-1)+x(k-1),
(2)
y(k)=g(W3x(k)+W5yc(k)),
(3)
yc(k)=α·yc(k-1)+y(k-1).
(4)
1.2 学习算法
OHF Elman网络只是在Elman网络的输出层节点中增加了结构单元2作为输入,所以误差对连接权W1,W2,W3偏导没有什么变化,因此它们的权值修正公式与Elman网络相同.
(5)

(6)
(7)
将误差对结构单元2到输出层的连接权W4求偏导,并令其等于零,得到权W4的修正公式
(8)

OHF Elman神经网络实质上是在前向神经网络的基础上,通过引入反馈信号,存储内部状态使其具备映射动态特征的功能,从而使系统具有适应时变特性的能力,使得其时间序列的预测性能较BP神经网络更好[9].但OHF Elman网络采用梯度下降算法修正网络权值,由于梯度下降算法本身具有学习速度较慢且容易陷入局部最小值的特点,导致学习效率较低[10].
2 改进的遗传算法
2.1 编码
由于神经网络的权值和阈值的学习是一个复杂的连续参数优化问题,所以编码采用实数编码方案.每个染色体由结构单元与隐层连接权值、输入层与隐层连接权值、隐层与输出层连接权值、输出层与结构单元2连接权值、自连接反馈因子这5部分组成.选取所有染色体中码长最大者作为其他染色体码长标准而进行编码.
具体算法如下:设隐层结点的最大个数值是Hmax,输入层和输出层结点个数分别是m、n,则进行编码的各个染色体码串长度均为
L=(n+m+1)×Hmax+m+1,
(9)
各染色体的有效码长为(h为各个染色体码串的隐层结点个数)
L′=(n+m+1)×h+m+1.
(10)
2.2 选择
遗传算法(genetic algorithm,简称GA)用于神经网络的一个方面是用遗传算法来学习神经网络的权值,也就是用GA来取代一些传统的学习算法以克服其缺陷[11-12].为了提高神经网络的选择能力,避免过早收敛,论文对遗传算法中算子的选择作了适当的改进.
在选择算子时,如果选择压力过大就会造成种群多样性迅速降低,形成早熟收敛.在遗传进化的初期,通常会出现一些超常的个体因竞争力突出从而控制了选择过程,使群体陷入局部最优.因此,通过改善适应度值和比较算子相似度来克服以上缺点.为了增加适应度值[6]的选择,提高选择能力,定义下式
(11)
其中:f′是一个已指定的适应度值,fmax是适应度值的上限,如果fmax未知,可以用当前的适应度最大值取代;fmin是适应度值下限,如果fmin未知,可以用当前的适应度值的最小值取代;f是当前的适应度值,α∈(0,1)且为随机数,主要用它来增加遗传算法的随机性并且使分母不为零.
从公式中可以看到,fmax和fmin之间差别较大时,可以适当地降低适应度值,以防优秀个体控制整个种群;fmax和fmin之间区别较小时,此式可以矫正较大的适应度值,种群中个体间距离会增加.此时,通过提高适应度值,避免了算法在最佳的解决方案附近左右摆动而出现难以收敛的现象.
为避免遗传算法中的过早收敛现象,以确保种群的多样性[13],引入相似的定义.
假设一个算子具有n个基因,由于采用实数编码,可以把两个算子看成两个向量X={x1,x2,…,xn},Y={y1,y2,…,yn}.定义一个距离e,且定义
(12)
如果d 相似度为种群中相似的个体类型总数占种群的比例.当种群中个体完全不相似时,相似度为0,当种群中个体完全相似时,相似度为1.相似度是衡量两个个体之间的相似程度的指标.相似度越小,种群中个体类型越多,分配得越平均.交叉作用不能保证种群的相似度在t→∞ 时达到最大,相似度的变化与初始种群的分布有关,当初始种群的所有个体都相同,交换操作不改变种群的相似度.变异操作可显著提高种群的多样性,但当t→∞变异操作使种群相似度达到最大值,变异率越大,相似度增加得越快. 相似度的提出,使在算子选择过程中容易地取出相似的个体,确保种群的多样性,同时适用于Elman神经网络,并在优化神经网络中发挥作用. 交叉是遗传算法的核心,是遗传算法区别于其他传统优化方法的重要标志.以概率对两个个体进行交叉操作产生新的两个个体,没有进行交叉操作的个体进行直接复制. 遗传算法引入变异算子可以提供初始种群不含的基因,或找回选择过程中丢失的基因,为种群提供新的内容.将个体基因以概率Pm由0变为1,或由1变为0.其中Pm若太低则可能使群体中的重要信息丢失,若太高则会使遗传算法趋于随机搜索.论文中选择Pm=0.2. OHF Elman神经网络算法的权值的确定,是通过不断的学习、训练按照某种确定的权值变化规则得到一个较好的权值分布.将改进的遗传算法引入Elman网络中用于优化网络的权值,可以解决Elman网络递归部分权值固定的缺点,避免网络易陷入局部最小值. 改进遗传算法优化OHF Elman神经网络模型实现的具体步骤如下: 步聚1 生成初始种群过程.随即产生初始种群,种群的大小是30个,其中每个染色体采用实数编码,每个染色体由结构单元与隐层连接权值、输入层与隐层连接权值、隐层与输出层连接权值、输出层与结构单元2连接权值、自连接反馈因子组成. 图2 改进的GA优化OHF Elman神经网络流程图 Fig.2 Flow chart of improved GA optimizingOHF Elman neural network 步聚2 将个体的适应度值排序,计算个体的评价函数,并按评价函数的大小排序,再计算评价适应度值,把它作为一个阈值,选择适应度值大于平均适应度值的个体. 步聚3 判断是否达到确定的进化代数或达到进化结束的条件,满足则跳到步聚6,不满足则进行下一步. 步聚4 按一定的交叉概率和变异概率产生新的个体. 步聚5 判断相似度,对新产生的个体进行评价.当相似度超过一定的阈值而引起进化减慢时,将相似的个体取出,进行高概率的变异操作,用产生的新个体替代原相似的个体. 步聚6 将最优个体按顺序拆分,作为Elman网络的连接权值和反馈因子. 步聚7 检查是否满足结束条件,结束条件设定为达到最大后代数则算法结束. 基于改进的GA优化OHF Elman神经网络流程图如图2所示. 以新疆某金矿实测氧化槽内的pH、温度、黄铁矿含量和氧化还原电位为原始值进行算法验证. 对于含砷难处理金矿石,在生物氧化预处理过程中氧化还原电位主要受pH、温度和黄铁矿含量的影响,所以OHF Elman神经网络的输入神经元个数为3个,输出神经元为1个.由于单隐含层就能实现任意函数逼近,设定隐含层为1层.根据经验公式和仿真实验确定隐含层神经元个数为10个,结构层与隐含层神经元数量相同.遗传算法中的种群规模设为20,进化次数为100次,交叉概率为0.4,变异概率为0.2. 由于原始数据量纲的划分不同,且数据值之间相差较大,利用(13)式对数据进行归一化处理,处理后的数据均在[0,1]内,消除了量纲的影响. (13) 选取平均相对误差和均方根误差作为模型的评价指标.评价指标计算公式如下 (14) (15) 表1为2种预测方法的误差比较,表2为2种模型对照表. 表1 2种预测方法的误差比较 表2 2种模型对照表 由以上2个表可以看出,采用GA-OHF Elman神经网络方法来预测氧化还原电位的平均相对误差为2.35,小于GA-BP神经网络[14]方法的5.69.GA-OHF Elman神经网络的均方根误差为6.13,小于GA-BP神经网络方法的10.06 .GA-OHF Elman神经网络方法相比GA-BP,平均迭代次数少很多,进入局部最优的概率相比也小很多,仅是0.009 2.综合比较而言,GA-OHF Elman模型预测效果优于GA-BP模型,表明论文提出的GA-OHF Elman模型用于氧化还原电位预测是合理可行的,模型具有较高的预测精度和较好的泛化能力. 在MATLAB平台上分别建立了GA-OHF Elman(如图3所示)、GA-BP 2种神经网络预测模型(如图4所示),对氧化槽内氧化还原电位进行预测. 图3 改进Elman神经网络预测图 图4 BP神经网络预测图 由图3、4可看出,用GA-Elman神经网络模型得到的预测值基本分布在实际目标值附近,而GA-BP模型得到的预测结果偏离目标值较大. 图5、6分别是两个预测模型的训练误差曲线,可以看出GA-Elman神经网络模型的训练误差比GA-BP神经网络模型的训练误差小. 图5 Elman神经网络训练误差曲线 图6 BP神经网络训练误差曲线 目前,对OIF Elman神经网络的研究较多,但对OHF Elman神经网络的研究较少.论文基于OHF Elman神经网络基本原理,针对Elman神经网络存在的学习速度较慢、易陷入局部极小值等缺陷,提出了一种GA优化OHF Elman神经网络连接权值的GA-OHF Elman模型,用于氧化还原电位预测.以新疆某金矿为例进行实例分析,结果表明GA-OHF Elman模型用于氧化还原电位的预测是合理可行的,模型具有较高的预测精度,为企业在控制给料中黄铁矿含量的比例提供了依据,促进了生物氧化提金技术的发展和完善,对于相关的研究起到了借鉴作用. 参考文献: [1] 李骞.含砷金矿生物预氧化提金基础研究[D].长沙:中南大学资源加工和生物工程学院,2007. [2] 郑晔.难处理金矿石预处理技术及应用现状[J].黄金,2009,30(1):36-41. [3] Arrascue M E L. Biooxidation of arsenopyrite concentrate using BIOX®process: industrial experience in Tamboraque, Peru[J].Hydrometallurgy,2006,83(1):90-96. [4] 杨松荣.含砷难处理金矿石生物氧化提金基础与工程化研究[D].长沙:中南大学资源加工和生物工程学院,2004. [5] 崔东文.改进 Elman 神经网络在径流预测中的应用[J].水利水运工程学报,2013,(2):71-77. [6] 唐朝伟,何国田,徐昌彪,等.神经网络在采煤工作面瓦斯涌出量预测中的应用[J].计算机应用,2007,27(B12):202-204. [7] Shi X, Liang Y, Lee H, et al. Improved Elman networks and applications for controlling ultrasonic motors[J].Applied Artificial Intelligence,2004,18(7):603-629. [8] Gao X Z, Ovaska S J. Genetic algorithm training of Elman neural network in motor fault detection[J].Neural Computing & Applications,2002,11(1):37-44. [9] 傅荟璇,赵红.MATLAB 神经网络应用设计[M].北京:机械工业出版社,2010. [10] Song Q. On the weight convergence of Elman networks[J].IEEE Trans Neural Netw,2010,21(3):463-480. [11] 刘威,李小平,毛慧欧,等.基于实数编码遗传算法的神经网络成本预测模型及其应用[J].控制理论与应用,2004,21(3):423-426. [12] 李松,罗勇,张铭锐.遗传算法优化BP神经网络的混沌时间序列预测[J].计算机工程与应用,2011,47(29):52-55. [13] 王芳,程水源,李明君,等.遗传算法优化神经网络用于大气污染预报[J].北京工业大学学报:自然科学版,2009,35(9):1230-1234. [14] Yang B, Su X H, Wang Y D. BP neural network optimization based on an improved genetic algorithm[C]∥Proceedings of the Machine Learning and Cybernetics, International Conference on IEEE,2002:141-146.2.3 交叉和变异
3 改进遗传算法优化OHF Elman神经网络

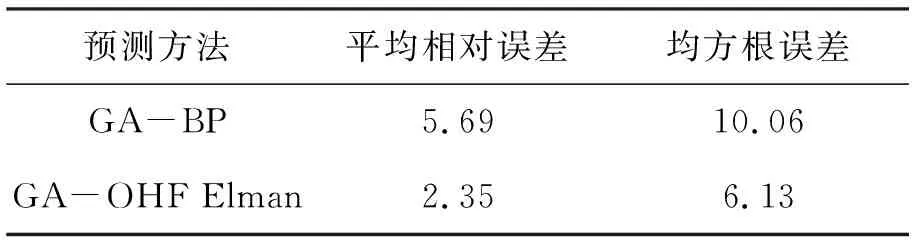
4 实验与分析








5 结束语

