交替方向块稀疏信号快速重构算法

康 凯，王粒宾，钟子发

(1.电子工程学院 通信对抗系,安徽 合肥 230037；2.第二炮兵工程大学信息工程系,陕西 西安 710025；3.解放军61922部队,北京 100094)

信号稀疏重构是压缩感知(compressive sensing,简称CS)[1]的核心问题之一.假设稀疏线性模型为b=Ax，其中，b为线性测量值，A为欠定的感知矩阵，x为待重构信号.在标准的CS框架下，重构x时仅仅限制x中非零元素的个数(即稀疏度)不能超过某一阈值k，并没有对非零元素的结构加以约束，也就是说，非零元素可以出现在x中的任何位置.但是在某些应用中，如多带信号重构[2]及子空间信号重构[3]等，x的非零元素呈聚集分布，此时称x满足块稀疏(block sparsity)模型.显然，块稀疏的x可以在标准CS框架下进行重构，但是将这种块稀疏结构加以利用，可以获得更好的重构性能，因此，块稀疏信号重构已成为最近的研究热点.

块稀疏信号重构算法可分为2类：一类为贪婪追踪类算法，如块正交匹配追踪[4-5](block orthogonal matching pursuit,简称Block OMP)和块压缩采样匹配追踪[6](block compressive sampling matching pursuit,简称Block CoSaMP)；另一类为凸松弛类算法，如基于二阶锥规划(second-order cone programming,简称SOCP)和内点法(interior point,简称IP)的SOCP+IP算法[3]，基于半定规划(semi-definite programming,简称SDP)和内点法的SDP+IP算法[7].贪婪追踪类算法的特点是计算量小，但重构误差大，且其计算量随着块稀疏度的增大而急剧增大；凸松弛类算法的重构精度高，但是现有基于SOCP和SDP的算法计量大，特别在大尺度问题下，计算量将是无法克服的困难.

应用凸松弛模型，作者提出一种基于交替方向法(alternating direction method,简称ADM)[8-9]的快速块稀疏重构算法(block-sparse recovery based on ADM,简称ADM-BSR)，通过仿真说明该算法的有效性.

1 问题说明

设线性测量值b∈RM，感知矩阵A∈RM×N，块稀疏信号x∈RN，加性噪声n∈RM，块稀疏模型如图1所示[7].

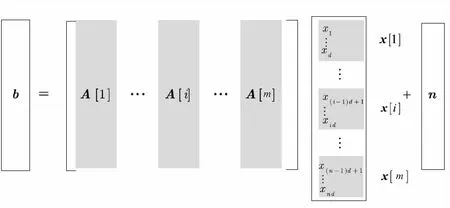
图1 块稀疏模型示意图

图1中，d为块长度，m为块数，满足N=dm.x[i]=(xd(i-1)+1,xd(i-1)+2,…,xdi)T表示第i个块，A[i]=(ad(i-1)+1,ad(i-1)+2,…,adi)表示对应于x[i]的子矩阵.块稀疏的数学模型为

(1)

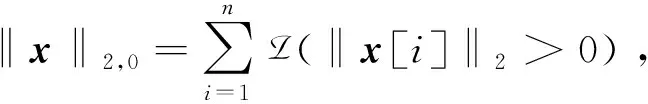
块稀疏重构的数学模型为[3,7]

(2)

其中:ε为噪声n的均方差.直接求解上式是NP-难的[7]，一类近似求解方法是对式(2)进行凸松弛，转化为凸优化问题[3,7]，即

(3)

式(3)称为块稀疏重构的l2/l1模型.l2/l1模型进行块稀疏重构的优势在于高精度，但是现有的SOCP+IP算法和SDP+IP算法计算量大，例如SOCP+IP的计算复杂度高达O(N3)[10]，由此可见在大尺度问题下上述2种方法不再适用.

针对此，该文目标是基于l2/l1模型提出一种快速块稀疏重构算法，在保持较高重构精度的前提下，提升计算效率.在此需要说明的是，在统计学领域Yuan等利用变量的组聚集特性，提出一种称之为group lasso[11]的问题模型.在group lasso中，目标函数为

(4)

其中:τ为正则化参数.

式(3)、(4)二者的不同点在于：式(3)中的参数ε具有明确的物理意义，其值大小与噪声的均方差成比例，设置容易；而式(4)中的τ值则很难选择.因此，在信号处理领域研究式(3)的求解更具有实际意义.

2 ADM框架

设f(x):RM→R和g(y):RN→R均为凸函数，B∈RP×M，C∈RP×N，w∈RP.考虑下述凸优化问题

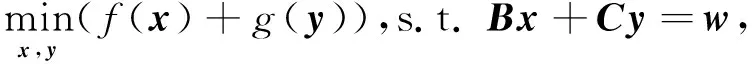
(5)

其中:变量x和y在目标函数中是可分离且可单独求解的，而在等式约束下则是相互关联的.

(5)式的增广拉格朗日函数为

(6)

其中:λ∈RP为乘子，β为惩罚因子.

利用ADM得到(6)式的迭代形式为

(7)

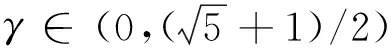
已经证明，在每次迭代中，若xk+1和yk+1能够精确求解，则ADM是收敛于式(5)的全局最优解[8].

3 基于ADM的块稀疏信号重构算法

在块稀疏信号重构l2/l1模型的基础上，利用ADM提出一种快速算法，称之为ADM-BSR算法，下面详细介绍ADM-BSR算法的推导过程.对式(3)进行变量分裂，可得

(8)

式(8)的增广拉格朗日函数为

(9)

利用ADM求解式(9)的迭代形式为

(10)

其中:PBε为到集合Bε≜{a∈RM：‖a‖2≤ε}上的正交投影算子.

式(10)的4个子问题中，nk+1、λk+1和βk+1均可得到闭式解，而xk+1只能通过迭代进行求解.考虑到x[i](i=1,…,n)是x中互不重叠的子块，因此选择BCD法[12]求解xk+1.为方便描述，定义dk=nk+1-b-λk/βk，目标函数转化为

(11)

可见F(x)是一个非光滑的凸函数.分别针对x[i](i=1,…,m)求次梯度，可得[13]

(12)

其中

定义

(13)

因此，由式(12)可得求解x[i]的KKT条件为

(14)

当x[i]≠0时，定义

(15)

对于随机测量矩阵，对其列进行标准正交化处理后，可假设AT[i]A[i]=I.将式(14)代入式(12)，则有

(16)

由式(15)、(16)可知，si与x[i]共线，因此有

(17)

4 ADM-BSR算法分析

4.1 计算复杂度

对于某一具体问题，无法估计ADM-BSR算法所需要的迭代次数.但是对于每次迭代， ADM-BSR算法仅需要向量与标量乘积运算、向量之间相加运算、子矩阵A[l]和AT[l]与向量的乘积运算、矩阵A与向量的乘积运算，不存在矩阵与矩阵乘积运算以及矩阵求逆运算，因此，相比于SOCP+IP算法和SDP+IP算法，ADM-BSR算法的计算量大大减少.

4.2 收敛性

首先，分析采用BCD方法求解xk+1的收敛性.Tseng在文献[12]中指出，若目标函数由一个光滑的凸函数和一个非光滑的块可分凸函数组成，在Gauss-Seidel循环规则下BCD方法可以保证得到全局最优解.显然，解xk+1的目标函数F(x)满足这个要求，并且在ADM-BSR中也可采取Gauss-Seidel循环规则，因此从理论上可以保证随着迭代次数的增加，xk+1可无限接近于F(x)的全局最优解.但是，在算法的实际实施过程中迭代次数往往有限，因此xk+1将不再是F(x)的最优解，而是次优解.这种情况下，子问题不能精确求解时，ADM的收敛性将难以证明.

然而，ADM-BSR算法利用BCD方法迭代求解xk+1时，以每个子块x[i]的KKT条件作为终止条件，可以保证xk+1非常接近于F(x)的最优解，且在迭代过程中不会出现发散现象，因此可以预测ADM-BSR算法是收敛的，大量仿真实验也证明了这点.

5 仿真实验

与文献[3-7]相同，进行综合实验.5.1节的仿真用于验证利用信号块稀疏特性可以提高重构精度；5.2节通过比较ADM-BSR算法、Block OMP算法[4]和Block CoSaMP算法[6]的仿真实验，说明ADM-BSR在计算效率上的优势.

5.1 块稀疏重构和标准稀疏重构的精度比较

在综合实验中，采取如下的仿真场景：感知矩阵A为一个M×N维随机矩阵，其元素独立且服从均值为0、方差为1/(2N)的高斯分布，其列进行标准正交化处理.线性测量值b=Axtrue+n，其中n为均值为0、方差为σ2的高斯白噪声.块长度设为d，则xtrue共有m=N/d个块，xtrue的K个非零块在[1,m]中随机选取，非零块中元素值服从标准高斯分布.与文献[14]相同，定义重构误差为均方误差(mean-squared error,简称MSE)，即

(18)

问题参数设置如下：测量维数M=2 048，信号维数N=4 096，噪声均方差σ=0.1，块稀疏度K=16，块长度d=64，标准稀疏度k=Kd=1 024.

图2 标准稀疏重构与块稀疏重构性能比较

从仿真结果可知，标准l1模型下重构误差为MSEl1=2.55×10-2，而l2/l1模型下重构误差仅为MSEl2/l1=4.028×10-4.因此，利用信号的块稀疏特性，可以大大提高重构精度.

5.2 ADM-BSR与Block OMP、Block CoSaMP计算效率的比较

仿真场景设置与5.1节相同.问题参数为M=2 048，N=4 096，σ=0.1，d=64，在块稀疏度K从6变化到30过程中计算3种算法的计算耗时和均方误差.设置Block CoSaMP和ADM-BSR的迭代次数为20，Block OMP的迭代次数与稀疏度K相同.仿真环境为Matlab R2008a，P4 2.6 G(双核)，1 G内存，Windows XP操作系统.

图3为3种算法的计算耗时随块稀疏度变化的曲线，图4为3种算法的均方误差随块稀疏度变化的曲线.仿真曲线为50次平均的结果.

图3 3种算法的计算耗时随块稀疏度变化的曲线

图4 3种算法的均方误差随块稀疏度变化的曲线

从图3、4可以看出：1)在计算耗时方面，ADM-BSR算法的计算耗时随着块稀疏度增加而基本保持不变，而Block CoSaMP和Block OMP则随着块稀疏度的增加急剧增加，自K=12(块稀疏比δ=K/m=0.18)起，ADM-BSR算法的计算耗时将小于贪婪追踪类算法.这直观说明了在高块稀疏度下，ADM-BSR的计算优势十分明显；2)在重构误差方面，总的来看，Block OMP的MSE最大，ADM-BSR和Block CoSaMP的相对较小.对于ADM-BSR和Block CoSaMP，在低块稀疏度时，两者的MSE非常接近，但随着块稀疏度增加，ADM-BSR的MSE小于Block CoSaMP的.

6 结束语

作者研究了块稀疏信号的重构问题.基于块稀疏重构的l2/l1模型，利用ADM提出一种ADM-BSR算法，分析了算法的计算复杂度和收敛性.通过仿真实验可以看出ADM-BSR算法的重构精度高于基于贪婪追踪的Block CoSaMP和Block OMP，且在块稀疏度较高时，计算耗时也远小于这2种算法.

参考文献:

[1] Candes E, Wakin B M. An introduction to compressive sampling[J].IEEE Signal Processing Magazine，2008,25(2):21-30.

[2] Mishali M, Eldar C Y. Blind multi-band signal reconstruction: compressed sensing for analog signals[J].IEEE Transactions on Signal Processing,2009,57(3):993-1009.

[3] Eldar C Y, Mishali M. Robust recovery of signals from a structured union of subspaces[J].IEEE Transactions on Information Theory,2009,55(11):5302-5316.

[4] Eldar C Y, Kuppinger P, Bolcsker H. Block-sparse signals: uncertainty relations and efficient recovery[J].IEEE Transactions Signal Processing,2010,57(6):3042-3054.

[5] Lv X, Wan C, Bi G. Block orthogonal greedy algorithm for stable recovery of block-sparse signal representations[J].Signal Processing,2010,90(12):3265-3277.

[6] Baraniuk G R, Cevher V, Duarte F M, et al. Model-based compressive sensing[J].IEEE Transactions on Information Theory,2010,56(4):1982-2001.

[7] Stojnic M, Paryaresh F, Hassibi B. On the reconstruction of block-sparse signals with an optimal number of measurements[J].IEEE Transactions Signal Processing,2009,57(8):3075-3085.

[8] Yang J, Zhang Y. Alternating direction algorithms for l1-problems in compressive sensing[R].Houston: Rice University,2009.

[9] Afonso V M, Bioucas-Dias M J, Figueiredo A M. Fast image reconvery using variable splitting and constrained optimization[J].IEEE Transactions on Image Processing,2010,19(9):2345-2356.

[10] Rakotomamonjy A. Surverying and comparing simultaneous sparse approximation (or group lasso)algorithm[J].Signal Processing,2011,91:1505-1526.

[11] Yuan M, Lin Y. Model selection and estimation in regression with grouped variables[J].Journal of Royal Statistical Society, Series B,2006,68(1):49-67.

[12] Tseng P. Convergence of block coordinate descent method for non-differentiable minimization[J].Journal of Optimization Theory and Application,2001,109:475-494.

[13] Bertsekas D, Nedic A, Ozdaglar A. Convex analysis and optimization[M].Nashua: Athena Scientific,2003.

[14] Wright J S, Nowak D R, Figueiredo A M. Sparse reconstruction by separable approximation[J].IEEE Transactions on Image Processing,2009,57(7):2479-2493.