基于Adomian分解法的变系数组合KdV方程的近似解
卢殿臣,沈芙蓉,洪宝剑
(江苏大学 非线性科学研究中心,江苏 镇江 212013)
随着非线性科学的蓬勃发展,非线性问题的求解一直是数学物理工作者研究的重要课题.然而,由于非线性问题的复杂性,绝大多数非线性微分方程没有精确解,人们不得不发展各类求近似解的方法.近几年发展起来的Adomian分解法[1-2]就是一种寻求非线性微分方程近似解的有效方法.这种方法可以获得具有较高精度的近似解,已经被广泛应用到许多带有孤立波解、有理函数解及其他形式解的非线性微分方程[3-9],充分体现了其适普性和高效性.对于常系数组合KdV方程,国内外学者已用各种方法作出了大量的结果[10-14].文献[15]利用Adomian分解法得到了常系数mKdV方程的近似解,而关于变系数组合KdV方程的研究很少.论文将用Adomian分解法求出变系数组合KdV方程的近似解.由于变系数方程更能准确刻画众多的物理现象,因此对其进行求解意义重大.
1 模型与Adomian分解法
讨论变系数组合KdV方程如下
ut+a(t)uux+b(t)u2ux+c(t)uxxx=0,
(1)
其中:a(t),b(t),c(t)是关于t的任意函数.
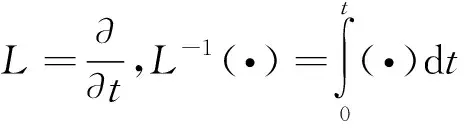
u(x,t)=u(x,0)-L-1(a(t)uux+b(t)u2ux+c(t)uxxx).
(2)
由Adomian分解法,可以令
(3)
(4)
其中:Ak为Adomian多项式[2],定义如下
于是,有
A0=a(t)u0u0,x+b(t)u0u0,x,
A1=a(t)u0u1,x+a(t)u1u0,x+b(t)u0u1,x+2b(t)u0u1u0,x,
A2=a(t)u0u2,x+a(t)u1u1,x+a(t)u2u0,x+b(t)u0u2,x+
2b(t)u0u1u1,x+2b(t)u0u2u0,x+b(t)u1u0,x.
将(2)式参数化,则有
(5)
比较上式两边关于λ的同次幂系数,可得递推式
u0=u(x,0),
uk+1=-L-1(Ak+c(t)uk,xxx).
(6)
利用Mathematic软件,可以逐步求出每一个uk(x,t),从而由(3)式,有
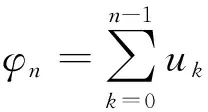
2 椭圆函数形式的近似解
如果在方程(1)中取a(t)=6t,b(t)=6t,c(t)=t,则方程(1)化为
ut+6tuux+6tu2ux+tuxxx=0,
(7)
考虑其初值条件
其中:k为任意常数,m为模数,0≤m≤1.
下列式子中cn(kx,m)为椭圆函数,满足
于是,有
u0,x=-k2mdn(kx,m)sn(kx,m),
u0,xxx=k4mdn(kx,m)sn(kx,m)(4mcm2(kx,m)+dn2(kx,m)-msn2(kx,m)),
3m)cn2(kx,m)-2k2dn2(kx,m)+2k2msn2(kx,m)),
4k2(-3+4k2m(-11+12m)cn2(kx,m))dn4(kx,m)-4k4dn6(kx,m)+
m((3+4k2(2-3m)m2(kx,m))2+8k2(21-18m+4k2m(41+
6m(-10+3m))cn2(kx,m))dn2(kx,m)-12k4(-45+
44m)dn4(kx,m))sn2(kx,m)+4k2m2(-3+k2(4m(-11+12m)cn2(kx,m)+
3(-45+44m)dn2(kx,m)))sn4(kx,m)+4k4m36(kx,m)).
u3=-L-1(6tu0u2,x+6tu1u1,x+6tu2u0,x+6tu0u2,x+
12tu0u1u1,x+12tu0u2u0,x+6tu1u0,x+tu2,xxx)=
msn2(kx,m)(-3+2k2msn2(kx,m))3+4k4dn6(kx,m)(9+8k2m(-307+
306m)sn2(kx,m))+64k4m3cn6(kx,m)(9(2-3m)2+k2(1 976-3 996m+
2 538m2-513m3)dn2(kx,m)+k2m(-1 976+3 996m-2 538m2+
513m3)sn2(kx,m))+6k2dn4(kx,m)(9+18k2m(-45+44m)sn2(kx,m)+
8k4m2(913-1 056m+144m2)sn4(kx,m))+dn2(kx,m)(27+108k2m(-7+
6m)sn2(kx,m)-108k4m2(-45+44m)sn4(kx,m)+32k6m3(-307+
306m)sn6(kx,m))+48k2m2cn4(kx,m)(18-27m+2k4(2 564-3 564m+
999m2)dn4(kx,m)-9k2m(76-116m+39m2)sn2(kx,m)+2k4m2(2 564-
3564m+999m2)sn4(kx,m)+k2dn2(kx,m)(9(76-116m+39m2)+
4k2m(-5 180+7 764m-2 853m2+270m3)sn2(kx,m)))+4mcn2(kx,m)(27+
4k6(1 884-1 845m)dn6(kx,m)+27k2m(-22+21m)sn2(kx,m)-3 672k4(-1+
m)m2sn4(kx,m)+4k6m3(-1 844+1 845m)sn6(kx,m)-12k4dn4(kx,m)(306(-1+
m)+k2m(10 820-13 449m+2 628m2)sn2(kx,m))+3k22(kx,m)(198-189m-
144k2m(43-52m+9m2)sn2(kx,m)+4k4m2(10 820-13 449m+2 628m2)sn4(kx,m)))).
…
因此,方程(7)的4级近似解为
φ4=u0(x,t)+u1(x,t)+u2(x,t)+u3(x,t).
(8)
3 数值模拟与误差分析
根据文献[16],方程ut+6uux+6u2ux+uxxx=0有精确解
由此不难推出方程ut+6tuux+6tu2ux+tuxxx=0有精确解
(9)
且满足
这正是方程(7)当m=1,k=1时的情形.
接下来,用数值模拟的方法给出m=1,k=1时方程(7)的近似解φ4与精确解式(9)的误差分析,如表1所示.

表1 方程的精确解、近似解以及绝对误差、相对误差
当m=1,k=1时,方程(7)的精确解与近似解φ4的3维立体图、等高线和密度图如图1~4所示.

图1 方程的精确解Fig.1 Exact solution

图2 方程的近似解 Fig.2 Approximate solution
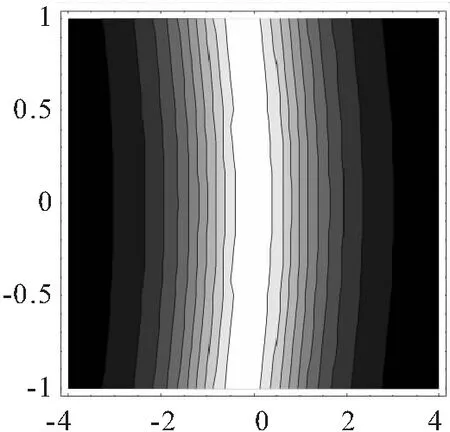
图3 方程近似解的等高线图Fig.3 The contour plot of the approximate solution

图4 方程近似解的密度图Fig.4 The density plot of the approximate solution
4 结束语
论文首次利用Adomian分解法求解带有初值条件的变系数组合KdV方程,得到了具有椭圆函数形式的近似解, 并进行了误差估计,给出了近似解的3维立体图、等高线图和密度图. 数值模拟的结果表明所求的4级近似解与其精确解高度相似.研究表明,Adomian分解法可应用于变系数非线性微分方程,而且可以根据需要通过增加计算项数来提高近似解的精确度.但是,如何将此方法应用于高阶高维的系统还有待于进一步研究.
参考文献:
[1] Adomian G. Solving frontier problem of physics: the decomposition method[M].Boston:Kluwer Academic Publishers,1994.
[2] Rach R A. Convenient computational form for the Adomian polynomials[J].J Math Anal Appl,1984,102:415-419.
[3] Wazwaz A M. Construction of solitary wave solutions and rational solutions for the KdV equation by Adomian decom-position method[J].Chaos Soliton Fract,2001,12:2283- 2293.
[4] Wazwaz A M. A sine-cosine method for handlingnonlinear wave equations[J].Mathematical and Computer Modelling,2004,40:499-508.
[5] Yan Z Y. New families of solitons with compact support for Boussinesq-likeB(m,n) equations with fully nonlinear dispersion[J].Chaos Soliton Fract, 2002,12:1151-1158.
[6] Kaya D, El-Sayed S M. An application of the decomposition method for the two-dimensional KdV-Burgers equation[J].Phys Lett A,2003,320:192-199.
[7] Zhu Y G, Lv Z S. New exact solitary-wave special solutions for the nonlinear dispersiveK(m,n) equations[J].Chaos Solitons and Fractals,2006,27:836-842.
[8] Dogan K. An application of the modified decomposition method for two dimensional sine-Gordon equation[J].Applied Mathematics and Computation,2004,159:1-9.
[9] Wazwaz A M. The decomposition method applied to systems of partial equations and to the reaction-diffusion Brusse-lator model[J].Appl Math Comput,2000,110:251-264.
[10] 闫振亚.组合KdV-mKdV方程的函数变换和精确解析解[J].烟台大学学报:自然科学与工程版,2001,14(2):95-99.
[11] 张玉峰,张鸿庆.组合KdV与mKdV方程Backlund变换及其一类精确解[J].大连理工大学学报,2001,41(4):392-395.
[12] 韦敏志,唐生强.KdV-mKdV方程及其级数解[J].桂林电子科技大学学报,2012,32(5):398-401.
[13] Wadati M. The exact solution of the modified Kortweg-de Vries equation[J].J Phys Soc Jpn,1972,32:1681-1687.
[14] Wazwaz A M. New sets of solitary wave solutions to the KdV, mKdV, and the generalized KdV equations[J].Communications in Nonlinear Science and Numerical Simulation,2008,13(2):331-339.
[15] Yan Z Y. Approximate Jacobi elliptic function solutions of the modified KdV equation via the decomposition method[J].Applied Mathematics and Computation,2005,166:571-583.
[16] 韩家骅,陈良,徐勇,等.组合及二维KdV方程的显式精确解[J].安徽大学学报:自然科学版,2004,28(1):35-41.

