椭圆曲线密码的选择明文侧信道攻击方法

熊莉英，王 玉，李 强，李慧云

(1.西南科技大学信息工程学院，四川绵阳621010;2.中国科学院深圳先进技术研究院集成技术研究所深圳电动汽车动力平台与安全技术重点实验室，深圳518055)

0 引言

随着公钥密码系统的迅速发展，许多基于数学困难问题的密码算法得以发明.公钥密码体制根据其所依据的难题一般分为三类:大整数分解问题类、离散对数问题类、椭圆曲线类.椭圆曲线上所有的点外加一个叫做无穷远点的特殊点构成的集合连同一个定义的加法运算构成一个Abel群.在等式mP=P+P+…+P=Q中，已知m和点P求点Q比较容易，反之已知点 Q和点 P求m却是相当困难的，这个问题称为椭圆曲线上点群的离散对数问题.椭圆曲线密码体制正是利用这个困难问题设计而来.1985年，Miller[1]和Koblitz[2]分别提出将椭圆曲线应用到密码学上，称为椭圆曲线密码算法(Elliptic curve cryptosystems，ECC).与其他的公钥密码算法如RSA相比，ECC需要较短的密钥长度即可达到相同的安全级别.RSA要求密钥长度至少为1024位，使其大数因数分解计算十分困难.相对而言，ECC只要求160位的密钥即可达到相同的安全级别.当RSA的密钥使用2048位时，与ECC的密钥使用234位获得的安全级别相当，而密钥长度却相差9倍，当密钥长度增加时，相同安全级别的RSA与ECC密钥长度之间的差距更大.ECC具有密钥短的显著优点，因此引起业界日益增长的研究和应用兴趣.

即使一些密码算法在理论上是计算性安全(Computationally secure)的，但通过侧信道(例如，时序、功耗、电磁辐射)可能泄漏密钥相关信息，因此密码算法可以通过侧信道分析进行攻击.在公钥密码算法范围内，简单功耗分析(SPA)[3]攻击是一种被普遍采用的技术:根据对密码设备在运算时的功耗进行分析获取密钥信息.当运行公钥算法的设备进行不同密钥位操作时，其即时功耗也会发生相应的变化.已有实验证明，标准RSA二进制实现中的模方操作和模乘操作可以通过SPA分析被区分开，模方操作对应密钥位0，相邻的模乘操作与平方操作对应密钥位1，这样使得攻击者可以获得密钥.ECC标准二进制算法中的点加和点倍操作类似RSA中的模方和模乘操作.同理，如果可以区分ECC实现中的点加和点倍操作，那么攻击者就可以获取ECC密钥.

为了克服这一缺点，目前大多数的RSA算法通过插入哑操作的方式:遵循相同指令顺序来执行模乘和模方操作，即在模方操作中也加入哑模乘(Dummy multiply).这种方法被认为是有效的简单功耗攻击(SPA)防御方法.许多ECC算法也遵循了这一思想，按照相同的指令顺序执行点加和点倍操作.因此，很难区分随机输入的点加和点倍差异.为了从功耗波形中获得更强的信息泄露，文献[4-7]提出了RSA的特殊选择明文攻击方法.Yen提出[7]利用输入“－1”作为明文来攻击上述使用哑乘运算的RSA算法.除了－1，同理可以使用输入值为X和 －X作为选择明文，该方法的基本概念是使用了－1这一特殊的输入数据，使得模乘和模方操作的差异得以强化，从而使得标准二进制RSA实现的所有密钥位都可以被清晰地获得.

然而，由于模运算同余的特性，文献[4，7]的作者承认上述适用于RSA模运算的选择明文攻击方法不能推广至ECC类型的密码算法，因为ECC中没有模运算同余操作.本文提出一种针对ECC的选择明文攻击方法:利用在域运算中，无穷远点和接近原点在点倍点加的标量乘法中的特殊性，可以区分点倍与点加.

1 ECC概述

椭圆曲线是一组满足K域上的二元三次齐次方程解的点(x，y)的集合，方程如下

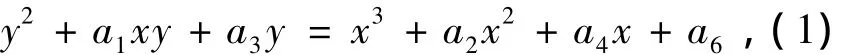
式中:ai∈K，该方程定义了一个K域上的椭圆曲线.方程(1)称为Weierstrass方程.

如果域 K的特征不等于2或3，方程(1)可以变换为

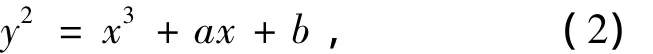
式中:a，b∈ K.

椭圆曲线上所有点加上一个特殊的无穷远点O，可以用下面给出的加法运算构成一个阿贝尔群结构.

当 charK≠ 2，3时的加法操作为:令点P=(x1，y1)≠O，－P=(x1，－y1).令点 Q=(x2，y2)≠O 且 Q≠－P，则和 P+Q=(x3，y3)可计算如下

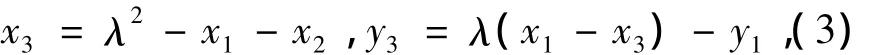
其中

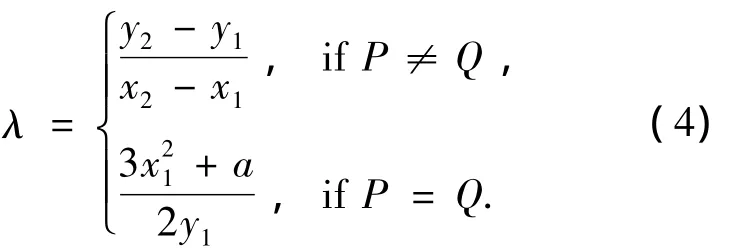
减去点P=(x，y)，可以用加上点 －P运算来代替.如果P≠Q，则运算 P+Q称为点加运算;如果P=Q则该运算称为点倍运算.图1说明了使用二进制算法自右向左(right-to-left)进行标量乘操作的过程.

图1 标量乘——二进制算法(right-to-left)Fig.1 Binary algorithm of scalar multiplication(right-to-left)

2 ECC二进制算法的选择明文与简单功耗攻击

为了防御简单功耗攻击，目前大多数标量乘都采用相同的指令序列来实现点加和点倍，比如引入哑操作，使得无论密钥位是1还是0，总是执行点加与点倍操作(Double-and-add-always)，或者采取更为复杂的原子化平衡操作[8]、蒙哥马利方法等.这样一来，使得在SPA攻击时得不到点加和点倍运算的显著功耗变化[9-12].为了在功耗波形中获得增强的信息泄露，本文提出选择特殊输入，其基本概念是利用一个输入点接近坐标轴，也就是说该特殊选取的点(xp，yp)作为输入，xp或yp值很小.例如，利用点P接近横轴(本文中记为Py→0)，或者接近纵轴(本文中记为 Px→0)来强化点加和点倍操作的差异.本文主要以接近横轴的点为例进行讨论，其他具有相同特性的点，同样适用于选择明文的SPA攻击.

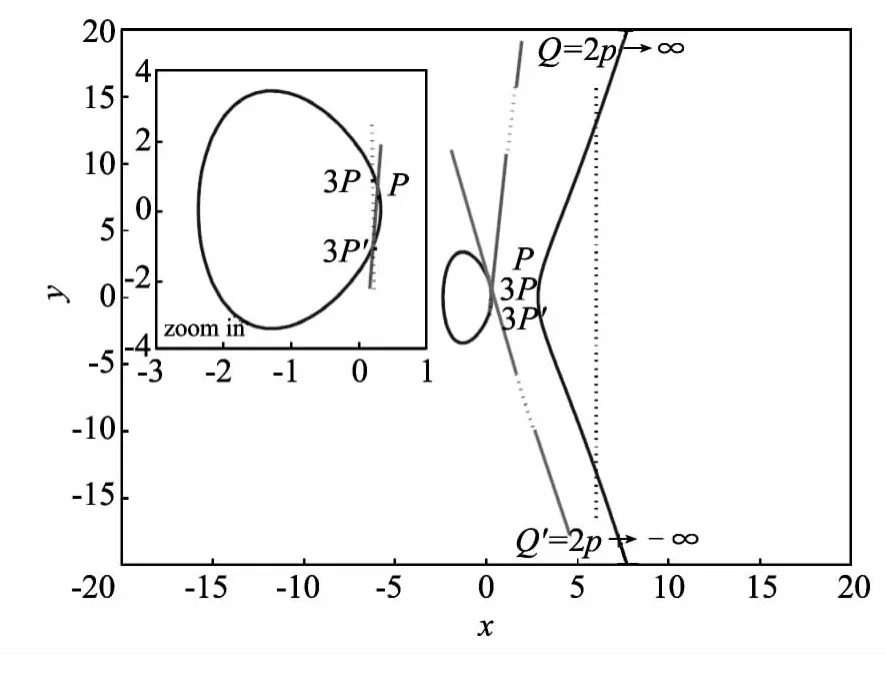
图2 ECC中靠近横轴的特殊选择点P的点加和点倍Fig.2 Point addition and point doubling in ECC with specially chosen input P close to X-axis

对输入 Py→0进行点倍运算:Q=2Py→0，会致使该点接近无穷远点，如图2所示.也就是说点的坐标值(xQ，yQ)变得极大，这将导致功耗的显著增大.本文中把这样的无穷远点Q记为Q∞.

由图1所示的二进制算法(right-to-left)可知，点加和点倍操作可以归纳为三种类型:(A)点加，(D1)点加后的点倍，(D2)点倍后的点倍.(D2)操作仅当正处理的密钥位为“0”时才发生.

假设P(x1，y1)为特殊选择明文，即y1趋于0，Q(x2，y2)为普通明文.

P+Q=(x3，y3)可计算如下

其中

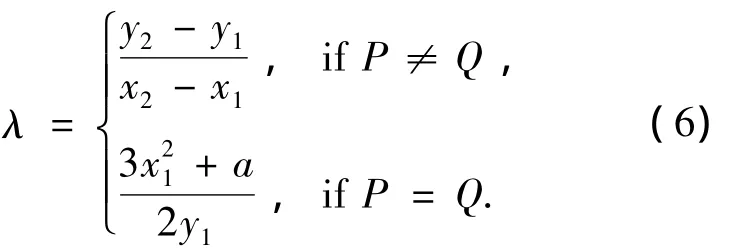
下面对A、D1、D2操作进行进一步分析:

因此，x3－A和 y3－A不为显著小或显著大值.

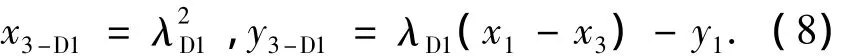
因此，x3－D1和 y3－D1为显著大值，且 x3－D1远大于 y3－D1.

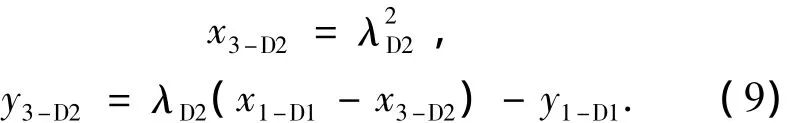
由于 λD2，x1－D1和 y1－D1都是较大值或显著大值.在芯片计算过程中，大数值运算需要频繁进行存储器读写，相对小数操作，功耗较大.因此，计算 x3－D2和 y3－D2比计算 x3－D1和 y3－D1的功耗更大.

另外 x3－D2为较大值，而 y3－D2不为显著大值，符合ECC代数几何图示中，特殊点的点倍后点倍的结果不为特殊点的直观认识.

由上述分析有，D2相比D1或A会消耗更大的功率.因此，即使原子化防御措施对标量乘实现中的点加和点倍操作进行了功率平衡，特殊选择的输入点Py→0仍然会使得D2明显地与D1或A区分开来.图3以侧信道轨迹模式示意D1、D2和A操作之间的差异.

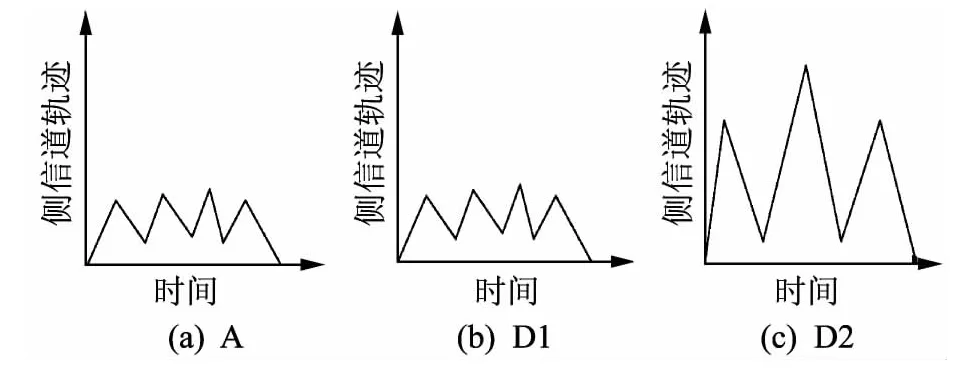
图3 特殊选择输入时的D1、D2和A操作比较Fig.3 Comparison between doubling(D1，D2)and addition(A)side-channel

因为D2仅在正处理的密钥位为“0”时出现，所以通过SPA就可以确定密钥位的顺序.以密钥位(部分)顺序“10100”为例，也即该密钥位形式如下:k=1zzz…00101|2，z表示1或0.表1是对密钥(部分)进行的二进制right-to-left算法.

表1 部分密钥位为“00101”从右到左的标量乘操作Tab.1 The scalar multiplication operation of the key with“00101”(right-to-left)

3 结论

本文提出了针对椭圆曲线算法的一种新型的基于选择明文的简单功耗分析攻击方法.所选择的特殊输入点P接近横轴或纵轴，是为了利用无穷远点或接近坐标轴的点的标量乘的特性:对坐标值小的点进行点加和点倍操作，会得到很大的坐标值变化.本攻击方法适用于所有的ECC标准二进制算法实现，即自右向左与自左向右算法.

[1]Miller V S.Use og elliptic curves in cryptography[C].Advances in Cryptology-CRYPTO’85 Proceedings.Berlin:Springer，1986:417-426.

[2]Koblitz N.Elliptic curve cryptosystems[J].Mathematics of Computation，1987，48(177):203-209.

[3]Kocher P C.Timing attacks on implementations of Diffie-Hellman，RSA，DSS，and other systems[C].Proceedings of 16th International Advances in Cryptology Conference-CRYPTO’96.Berlin:Springer，1996:104-113.

[4]Miyamoto A，Homma N，Aoki T，et al.Enhanced power analysis attack using chosen message against RSA hardware implementations[C].IEEE International Symposium on Circuits and Systems(ISCAS).USA:IEEE，2008:3282-3285.

[5]Novak R.SPA-based adaptive chosen-ciphertext attack on RSA implementation[J]. ComputerScience，2002(2274):252-262.

[6]Boer B D，Lemke K，Wicke G.A DPA attack against the modular reduction within a CRT implementation of RSA[J].Computer Science，2003(2523):228-243.

[7]Yen S M，Lien W C，Moon S J，et al.Power analysis by exploiting chosen message and internal collisions-vulnerability of checking mechanism for rsa-decryption[J].Computer Science，2005(3715):183-195.

[8]Chen T，Li H，Wu K，et al.Countermeasure of ECC against side-channel attacks:balanced point addition and point doubling operation procedure[C].Asia-Pacific Conference on Information Processing，2009:465-469.

[9]Coron J S.Resistance against differential power analysis for elliptic curve cryptosystems[J].Computer Science，1999(1717):292-302.

[10]Li H，Wu K，Xu G，et al.Simple power analysis attacks using chosen message against ECC hardware implementations[C].World Congress on Internet Security(WorldCIS-2011).London:IEEE，2011:68-72.

[11]李浪，杨柳，李肯立，等.一种椭圆曲线密码算法ECC旁路攻击方法研究[J].计算机应用研究，2013，30(3):889-890.Li Lang，Yang Liu，Li Kenli，et al.Research on sidechannel attack methods of ECC[J].Application Research of Computers，2013，30(3):889-890.(in Chinese)

[12]姚剑波，张涛.抗侧信道攻击的椭圆曲线密码算法[J].计算机应用与软件，2013，30(5):203-205.Yao Jianbo，Zhang Tao.ECC algorithm for preventing side-channel attck[J].Computer Application and Software，2013，30(5):203-205.(in Chinese)