一种基于邻域样本密度的SVDD样本剪辑方法及其应用

张安安，郑 萍，方 琳，彭嵩松

(1.江西省科学院能源研究所，330029，南昌；2.南昌师范学院，330032，南昌；2.江西警察学院刑事科学技术系，330100，南昌；4.井冈山大学电子与信息工程学院，343009，江西，吉安)

一种基于邻域样本密度的SVDD样本剪辑方法及其应用

张安安1，郑 萍2，方 琳3，彭嵩松4

(1.江西省科学院能源研究所，330029，南昌；2.南昌师范学院，330032，南昌；2.江西警察学院刑事科学技术系，330100，南昌；4.井冈山大学电子与信息工程学院，343009，江西，吉安)

通常对于大数据的学习问题，需要选择一个训练集的子集来进行学习，以降低问题本身的时间和空间复杂性。有很多学者从样本的近邻出发来选择样本，根据样本的近邻特点寻找位于靠近分类面的样本。对于SVDD(Support Vector Data Description)算法而言，只有位于数据集边缘区域的样本对学习结果有影响。提出了通过估计样本领域样本概率的方式来判断样本在数据集里的位置，位于数据集边缘区域的样本概率要明显小于位于数据集内部样本的概率，通过删除位于数据集内部的样本可以大大降低数据集的规模，在不降低算法的性能时，降低训练模型的复杂度，提高识别速度和算法的学习速度。并在实时性要求比较高的电能扰动信号识别方面，得到了很好的应用。

训练集；样本；SVDD；样本剪辑；电能质量扰动信号识别

0 引言

与SVM(Support Vector Machine)类似，一分类SVDD(Support Vector Data Description)[1-2]根据结构化风险最小化原理，通过求一个包含尽可能少的奇异点数据，并且体积尽可能小的球体来描述样本数据，即求满足下式的R和a：

s.t.:‖xi-a‖≤R2+ξi,ξi≥0

(1)

将式(1)化为Wolf对偶形式：

s.t.:0≤αi≤C

(2)

对于测试数据z是否为奇异点根据式(3)判断：

αj(xi,xj)≤R2

(3)

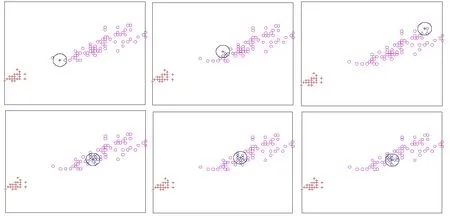
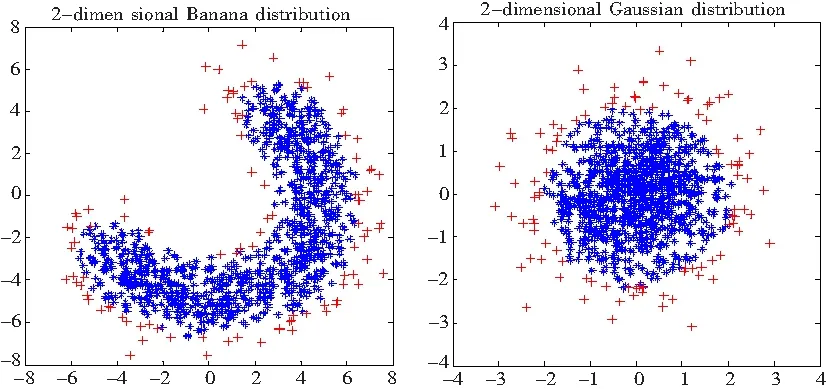
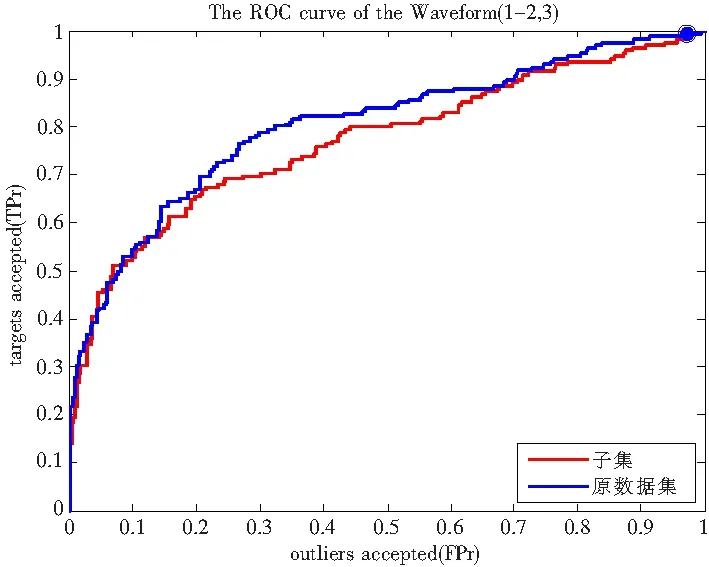
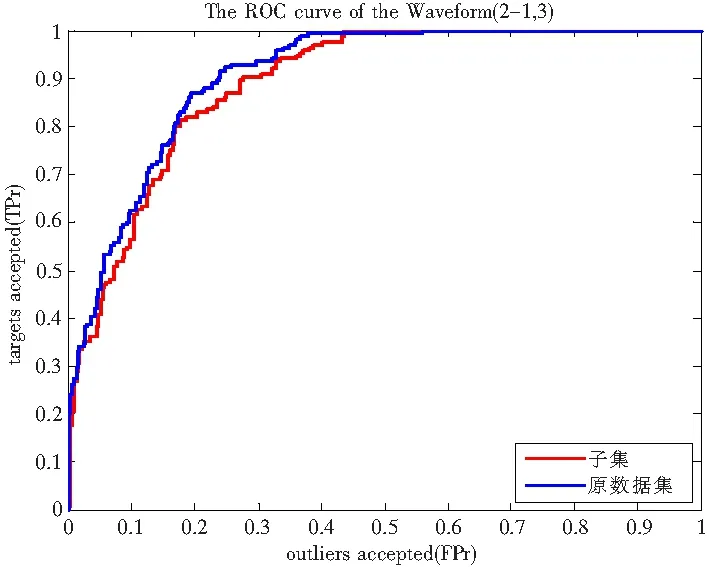
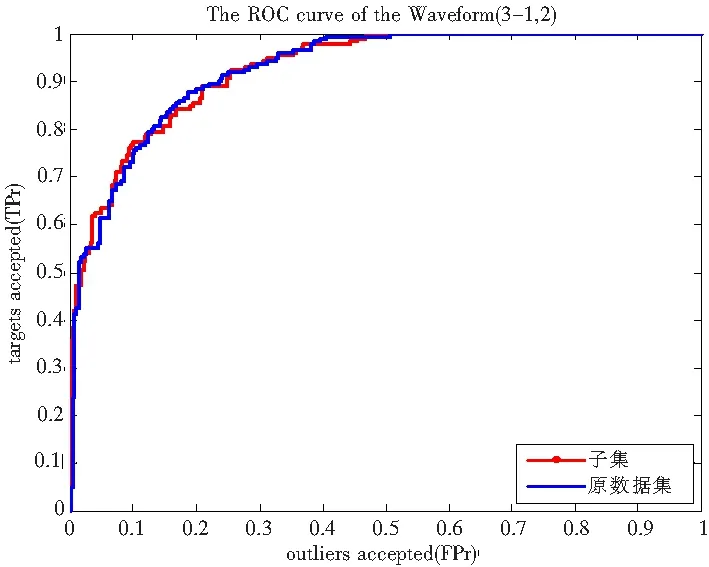
球半径可以根据式(4)求出，其中xk∈SV

αk

(4)

求式(2)就是解一个二次规划问题，因此SVDD也存在与求解SVM(Support Vector Machine)[3-4]问题相同的时间和内存问题。SVDD求出的数据描述只与支持向量有关，而与数据分布内部的样本没有关系。支持向量是靠近数据分布边缘的少量样本，而与占数据集大部分位于数据分布内部的样本无关。因此如果可以去除位于数据分布内部的样本就可以大大减少训练数据集的大小，而性能不会受太大影响。

图1 ‘+’表示目标数据，实线表示数据描述，实线外的是奇异数据(outlier)

对于已有的样本剪辑方法[5-9]大多数都是针对二分类和多分类问题。本文通过样本邻域的概率密度判断样本在数据集里的位置。通常，数据集内部样本位于高密度区域，而数据集边缘样本位于低密度区域。在数据集内部的样本可以通过估计邻域样本密度在SVDD算法训练前去除，而不影响算法的性能。

1 基于邻域样本密度的样本剪辑算法

图2为Iris数据集不同位置的样本密度情况。Iris数据总共有3类、4维。为了作图方便，图2只选取了样本中的2维。‘+’表示Versicolour类的样本，‘*’表示Setosa或Virginica类中的样本。‘◇’表示‘*’的近邻，‘o’表示‘*’的非近邻。第1行是位于数据集边缘；第2行是位于数据集内部。显然，位于数据集内部的样本密度要大于位于数据集边缘的样本密度。表1统计了图2不同位置邻域里的样本数量。

图2 Iris数据集不同位置样本邻域里近邻数不同

表1 Iris数据集样本邻域近邻数

用p(x)表示数据集D的概率分布函数，Si表示样本xi表的邻域。根据邻域密度可以定义数据集边缘的样本如下：

算法：

输入：D训练数据集；

输出：D′剪辑后的训练集。

步骤：

1)选取一个固定大小的邻域；

2)计算该邻域里的样本数；

3)选取一个合适的阈值(th)，如果邻域里样本数小于阈值保留；反之，丢弃；

4)由保留的样本组成新的数据集D′；

5)在新的数据集D′训练分类器。

算法第3)步保留的邻域内样本数小于阈值的样本即为位于数据集边缘的样本。为了避免混淆，本文以下内容将邻域球里的样本称为邻域里的近邻。

在该算法里有2个参数需要确定：邻域的大小和确定样本是否被保留的阈值(th)。邻域不能设置太大，否则无论样本是位于数据集边缘还是位于数据集内部，邻域内都可能包含过多的样本而无法区分样本在数据集中的位置；反之，邻域也不能太小，否则位于数据集内部的样本的邻域也可能包含很少的样本而无法区分。本文采用球形邻域，邻域球大小由球半径决定，邻域球半径可以指定一个常数或者通过选取样本集的一个较小的子集，用这个子集k近邻半径的平均值来表示邻域球的半径。阈值(th)决定被保留的子集的大小，阈值(th)越大，保留的样本越多；反之，保留的样本越少。本文根据需要保留的样本数量来确定阈值。

图3统计了2维Banana分布和2维高斯分布邻域内近邻数量的直方分布图。可以看到无论Banana分布还是高斯分布邻域内近邻数量小于20都只有少部分。图4根据邻域内近邻数量直方分布图找到的位于数据集边缘的样本。‘*’对应图3中邻域内近邻数量多于20的样本；‘+’对于图3中邻域内近邻数量少于或等于20的样本。

图3 邻域内近邻数量直方分布图

图4 根据邻域内近邻数量找出的边缘样本

图5表示仅保留图4中位于数据分布边缘的样本后由SVDD算法学习得到的数据描述。可以看到在保留的少部分样本上学习得到的数据描述可以很好的描述原数据集。

图5 由保留的边缘样本学习得到的数据描述

在不考虑其他优化方式时，计算一个样本的邻域内近邻数量需要计算该样本与其余样本之间的两两距离，因此算法在最坏的情况下时间复杂度为O(n2)。

2 实验与仿真

与其他分类方法一样，本文所有实验分别比较了ROC(Receiver Operating Characteristic) 曲线[10]和AUC(Area Under the receiver operating Characteristic)值[11]，并作为评价算法的标准。所有实验在Intel CoreTM2 Duo CPU E7200 @2.53 GHz,2 GB,windows XP机器上完成。为了验证算法的有效性，本文分别采用了人工数据集、UCI数据集[12]以及电能扰动信号模拟数据集。

2.1人工数据集

本实验采用Banana、Highleyman、Lithuanian、two difficult classes、5维高斯分布、10维高斯分布，这6个人工数据集。其中每个数据集训练样本由2 000个目标数据组成，测试集有目标数据和奇异数据共4 000个组成。邻域球半径取为50个样本的20个近邻组成的邻域球半径的平均值。实验比较了算法的时间、保留的数据集大小以及模型包含的支持向量数量。实验结果如表2～表5所示。其中表2的百分比表示子集保留的样本数占原数据集的百分比；表3比较了子集与原数据集的AUC值；表4比较了子集与数据集支持向量数量；表5子集算法时间包括算法预处理时间和子集训练时间。

表2 算法保留的样本

表3 AUC值比较

表4 支持向量数比较

表5 算法时间比较

由实验结果可以看到，在仅保留位于数据分布边缘的样本，算法的性能并没有降低，而模型的复杂度和算法的时间都得到了显著的提高。

2.2UCI数据集

为了进一步说明本文算法的有效性，本实验采用了3个常用的UCI数据集：Blood Transfusion、Mush Version 1和Waveform，数据集信息如表6所示。为了使这些数据集可以用于一分类，本文将Blood Transfusion和Mush Version 1中包含较多样本的类作为目标数据，另一类作为奇异数据；Waveform包含3类，分别被转换为3个一分类问题：1vs23,2vs13和3vs12，前一类作为目标数据，后两类作为奇异数据。算法分别比较了AUC值、ROC曲线。选择的样本仅占原数据集的10%左右。

表6 UCI数据集信息

表7 UCI数据集AUC值比较

图6～图10为UCI数据集的ROC曲线，点线表示子集的ROC曲线，实线表示原数据集的ROC曲线。

图6 Blood Transfusion的ROC曲线

图7 Mush Version1的ROC曲线

图8 Waveform 1vs23的ROC曲线

图9 Waveform 2vs13的ROC曲线

图10 Waveform 3vs12的ROC曲线

由图8～图10可以看出Waveform 1vs23、Waveform 2vs13和Waveform 3vs12的ROC曲线非常吻合；Blood Transfusion和Mush Version 1的ROC曲线虽然存在较大差异，但是从表7可以看出AUC值相差不是很大。而这些数据集的平均AUC值非常接近。表8比较了算法的时间和需要的支持向量数。与人工数据集的实验结果一样，在仅保留位于数据集边缘的样本时，SVDD模型的复杂性和算法时间都得到了很大的改进。子集上的支持向量数大约仅为原来的1/10，所需的时间大约仅为原来的1/4。

表8 UCI数据集AUC值比较

2.3模拟电能质量扰动信号集

电能质量扰动信号识别需要对常见的6种信号(电压闪变、电压谐波、电压中断、电压振荡、电压暂降和电压暂升)进行识别分类。支持向量机解决多分类问题的方式一种是通过将其中一类作为正类，其他类作为负类，即一对多方式，这种方式需要p个二分类器(p表示多分类类别数)。由于负类包含了p-1类的样本，因此负类的样本会远多于正类样本，这样转换二分类数据集就会引起数据集不平衡问题；另一种方式是将p类数据转换为p(p-1)个二分类问题，即一对一方式，这样需要p(p-1)个二分类分类器[13]。本文将多类问题转换为多个一分类问题，即分别以电压闪变、电压谐波、电压中断、电压振荡、电压暂降和电压暂升做为一分类问题的目标数据，其它类作为一分类问题的奇异数据，对这6类电能质量扰动信号识别问题就转换为6个一分类问题。本文首先对电能扰动信号数据进行剪辑，然后再将剪辑后的数据进行训练，剪辑后的数据约占原来数据集的10%左右。

电能质量扰动信号由matlab模拟而成，波长为4个周期，每个周期0.02 s，电压频率为50 Hz，采样频率12.8 kHz，其中电压闪变3 053个样本，电压谐波4 032个样本，电压中断1 872个样本，电压振荡3 096个样本，电压暂降2 614个样本，电压暂升2 517个样本。对于模拟得到的时域数据，首先利用db4小波[14-16]进行6层分解得到1 062维小波变换后的小波系数和尺度系数。然后利用主成分分析方法[17]保留约90%的信息。每类电能扰动信号数据被分为相互独立的10份，其中9份被作为训练数据，剩余的一份与其他5类数据作为测试数据，这样重复10次。表9、表10分别比较了原数据集与剪辑后的数据集的AUC值、精度、时间和模型复杂性，其中模型复杂度主要比较了模型中的支持向量数。

表9 电能质量扰动信号数据精度比较

由表9可以看出在剪辑后的数据集上无论是AUC值还是识别精度都与原数据集相差无几。而在保留原来性能的情况下，由表10可以看到在剪辑后的数据集上需要保留的支持向量和算法所需要的时间都比原数据集有所改进。

3 结论

SVDD算法与SVM算法类似需要求解二次规划问题，时间和空间复杂度都比较高。SVDD的结果仅有数据集中部分支持向量决定，而这样的支持向量通常位于数据集的边缘，因此仅保留数据集边缘的样本不会降低算法的性能。本文提出通过邻域样本密度来寻找位于数据集边缘的样本。人工数据集和UCI标准数据集的实验结果表明经过邻域密度剪辑过的数据集性能与原数据集的性能相比没有下降，算法的训练时间和模型的复杂性都得到了改善。在电能质量扰动信号识别问题方面也得到了很好的应用。

图10电能质量扰动信号数据时间、模型复杂度比较

数据集 支持向量数 时间/s 子集原数据集子集原数据集电压闪变897310．0520．781电压谐波717720．0570．915电压中断463810．0230．502电压振荡616200．0490．792电压暂降555060．0340．624电压暂升514890．0310．603平均62．2583．20．0410．703

[1] Tax D M J.One-class classification[D].Deflt:Delft University of Technology,2001.

[2]Tax D M J,Duin R P W.Support vector data description[J].Machine Learning,2004,54:45-66.

[3]蒋莎,张晓龙.一种用于非平衡数据的SVM学习算法[J].计算机工程,2008,34(20):198-199.

[4]Nello Cristianimi,John Shawe-Taylor.An Introduction to Support Vector Machines and Other Kernel-based Learning Methods[M].Beijing:China Machine Press,2005.

[5]Shin H,Cho S.Neighborhood property-based pattern selection for support vector machines[J].NeuralComput,2007,19(3):816-855.

[6]Chang E Y.Concept boundary detection for speeding up svms[C].ICML06: Proceedings of the 23rd International Conference on Machine Learning,2006:681-688.

[7]Almeida M B,Braga A,Braga J P.SVM-KM:speeding SVMs learning with a priori cluster selection and k-means[C].Proceedings of the 6th Brazilian Symposium on Neural Networks,2000:162-167.

[8]Zheng S F,Lu X F,Zheng N N,etal.Unsupervised clustering based reduced support vector machines[C].

Proceedings of IEEE International Conference on Acoustics,Speech,and Signal Processing (ICASSP) 2,2003:821-824.

[9]Koggalage R,Halgamuge S.Reducing the number of training samples for fast support vector machine classification[J].Neural Inf Process,2004,2(3):57-65.

[10]方景龙,王万良,何伟成.用于不平衡数据分类的FE-SVDD算法[J].计算机工程,2011(6):157-159.

[11]Bradley A.The use of the area under the ROC curve in the evaluation of machine learning algorithms[J].Pattern Recognition,1997,30(7):1145-1159.

[12]Blake C,Keogh E,Merz C.UCI repository of machine learning databases[EB/OL].http://www.ics.uci.edu/mlearn/MLRepository.html,University of California,Irvine,Dept.of Information and Computer Sciences,1998.

[13]Kressel U.Pairwise classification and Support Vector Machines,Cambridge[M].Massachusetts:MIT Press,1999:255- 268.

[14]陈珍萍,欧阳名三,刘淮霞.小波能量差分布和SVM结合的PQD识别[J].计算机工程与应用,2011(20):241-244.

[15]王成山,王继东.基于小波包分解的电能质量扰动分类方法[J].电网技术,2004,28(15):78-82.

[16]赵俊,杨洪耕,李伟.利用S变换与变尺度模板标准化的短时电能质量扰动分类[J].南方电网技术,2010,4(3):72-76.

[17]何朝晖.基于小波变换和人工神经网络的电能质量扰动分类[D].长沙:湖南大学,2009.

ASampleReductionMethodforSVDDandItsApplication

ZHANG Anan1,ZHENG Ping2,FANG Lin3,PENG Songsong4

(1.Energy Research Institute,Jiangxi Academy of Sciences,330029,Nanchang,PRC;2.Nanchang Normal University,330032,Nanchang,PRC;2.Department of Criminal Science and Technology,Jiangxi Police College,330100,Nanchang,PRC;2.School of Electronic and Information Engineering,Jinggangshan University,343009,Ji′an,Jiangxi,PRC)

Usually for large data learning problems,we need to select a subset of training set to study,in order to reduce the time and space complexity of the problem itself.Many scholars proposed to find useful samples,which locate near the boundary of the data distribution,based on K-nearest neighbors.The SVDD (Support Vector Data Description) algorithms,only in the edge region of the sample Data sets,have an effect on learning results. In this paper,a novel method to identify whether a sample locates near the boundary region by estimating the probability density of a neighborhood area.The probability density of a sample locating boundary region is much larger than the probability density of the sample locating in the internal of the data distribution.Removing the samples locating in the internal of the data distribution,the scale of training set can reduced heavily,the speed of training can be fast and the performance will not deteriorate.For power disturbance signal recognition problem,which is a real-time problem,this algorithm had a good application.

training det;dample;dupport vector data description;sample reduction;power disturbance signal recognition

2014-09-04;

2014-10-08

张安安(1979-)，女，江西吉安人，本科，副研究员，研究方向：计算机软件工程。

10.13990/j.issn1001-3679.2014.06.031

TP181

A

1001-3679(2014)06-0884-07