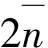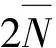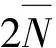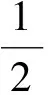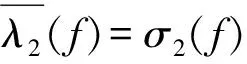二阶亚纯函数系数非齐次线性微分方程解的超级

梅 芳，刘 章，曾春华

(江西农业大学理学院，330046,南昌)

二阶亚纯函数系数非齐次线性微分方程解的超级

梅 芳，刘 章，曾春华

(江西农业大学理学院，330046,南昌)

研究了二阶亚纯函数系数非齐次线性微分方程f″+Af′+Bf=F解的超级不同零点收敛指数。当其系数满足一定的条件时，得到方程解的超级零点收敛指数的精确的估计。

亚纯函数；非齐次线性微分方程；超级不同零点收敛指数

1 背景

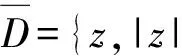
在文献[4]中，得到了下面的引理。

引理A：设A、B、F≢0为有限级亚纯函数，A、B为超越的，且满足

σ(A)<σ(B)<∞

(1)

和

(2)

若方程

f″+Af′+Bf=F

(3)

有亚纯解，则

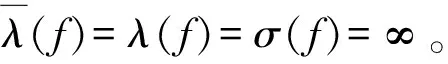
2 引理

引理1[6]：假设g(z)为亚纯函数，σ(g)=β<+∞，那么对任意给定的ε>0，存在一个线测度和对数测度都为有穷的集合E1⊂(1,+∞)，使当|z|=r∉[0,1]∪E1,r→+∞时|g(z)|≤exp{rβ+ε}。

引理3[8]：假设f(z)是超越亚纯函数，设P={(k1,j1),…,(km,jm)}表示一个整数对的有限集合，满足ki>ji≥0，(i=1,2,…,m),α>1是一个给定常数，那么存在子集E3⊂(1,+∞)有有穷对数测度，存在仅依赖α和P的常数K>0，满足对所有满足|z|=r∉[0,1]∪E3的z和(k,j)∈P，得到

3 主要结果

1996年Kwon Ki-Ho在文献[5]中研究了二阶线性整函数系数微分方程

f″+A(z)f′+B(z)f=0

的解的超级问题。

本文在文献[5]的启发下主要研究了引理A中无穷级解的超级，进一步深化了对方程(3)解的讨论，得到以下结果。

定理：设A、B、F≢0为有限级亚纯函数，A、B为超越的，且满足条件

max{σ(F),σ(A)}<σ(B)<∞

(4)

和

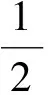
(5)

定理的证明：取α,β>0，使得σ(A)<α<β<σ(B)<+∞，先将方程式(3)改写为

(6)

由引理1可知，存在线测度和对数测度均有穷的集合E1⊂(1,+∞)，使|z|=r∉[0,1]∪E1,r→+∞时，

|A(z)|≤exp{rα}

(7)

由定理的条件(5)可知

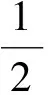
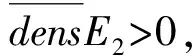
|B(z)|≥exp{(1+o(1))rσ(B)-ε}

(8)

设f为方程(3)的无穷级解，则f为超越亚纯函数，由引理3可知，存在一个子集E3⊂(1,+∞)具有有穷对数测度及常数K>0，对满足|z|=r∉[0,1]∪E3的所有z有

(9)

若f在z0有k(≥1)阶极点，而A(z),B(z)都在z0点解析，则f″+Af′+Bf在z0有k+2阶极点，但F在z0解析，矛盾，所以f的极点只能发生在A(z),B(z),F(z)的极点处，因此λ(1/f)<+∞。

F为有限级亚纯函数，f为无穷级亚纯函数，由Hadamard定理，可以表示f为f(z)=g(z)/d(z)，其中g(z),d(z)为整函数，满足

σ(g)=σ(f),λ(d)=σ(d)=λ(1/f)<σ(f)=+∞。

则

令ρ=σ{d(z)F(z)}=max{σ(d),σ(F)}<∞，由引理1，对任给的ε>0，存在一个线测度和对数测度都为有穷集合E4⊂(1,+∞),使当|z|=r∉[0,1]∪E4，r→+∞时，

|F(z)d(z)|≤exp{rρ+ε}

(10)

即

M(r,g)≥exp{rρ-α+ε}

(11)

由式(9)和式(10)可得，当|z|=r∈E5-{[0,1]∪E4}且r→+∞时，在|g(z)|=M(r,g)的点z处有

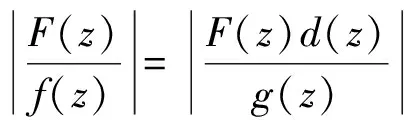
(12)

由式(6)～式(9)，式(12)可得，当|z|=r∈E2∩E5-{[0,1]∪E1∪E3∪E4}且r→+∞时

exp{(1+o(1))rβ}≤3Kr[T(2r,f)]3exp{rmax{α,ρ+ε}}

(13)

由于α<β，σ(d)<σ(f)，σ(F)<σ(B)及ρ=max{σ(d),ρ(F)}，可取到ε，使ρ+ε

σ2(f)≥σ(B)

(14)

由式(3)可知，如果f在点z0有α(>2)阶零点，A、B在点z0解析，则F必在z0有大于等于α-2阶零点。若F≢0，将式(3)改写为

则有下式成立

(15)

再应用对数导数引理知，至多除去一个线测度为有穷的r值集合E6外，有

m(r,1/f)≤m(r,1/F)+m(r,A)+m(r,B)+m(r,f″/f)+m(r,f′/f)+log 3=m(r,1/F)+m(r,A)+m(r,B)+O{log[rT(r,f)]}(r∉E6)

(16)

由式(15)和式(16)得到

(17)

又

(18)

T(r,F)+T(r,A)+T(r,B)≤3rσ(B)

(19)

由式(17)～式(19)可知

因此

(20)

则由式(14)、式(20)得

(21)

[1] 杨乐.值分布论及其新研究[M].北京:北京科学出版社,1982:1-109.

[2]何育赞,肖修冶.代数体函数与常微分方程[M].北京:科学出版社,1988.

[3]Hayman W.Meromorphic Functions[M].Oxford: Clarendon Press,1964:1-97.

[4]易才凤,边年英.二阶微分方程亚纯解的零点收敛指数和增长级[J].江西师范大学学报,1998,22(1):16-20.

[5]Kwon K H.On the growth of entire functions satisfying seand order linear.differential equtions[J].Bull Kvrean Math Soc,1996,35:487-496.

[6]陈宗煊.二阶亚纯系数微分方程亚纯解的零点[J].数学物理学报,1996,16(3):276-283.

[7]Chen Z X.The growth of solutions of second order linear differential equations with meromorphic coefficients[J].Kodai Math,1999,22(2):208-221.

[8]Gundersen G.Estimates for the logarithmic derivative of a meromorphic function plus similar estimates[J].London Math Soc,1988,37(2):88-104.

TheGrowthofSolutionsofSecondorderNon-homogeneousLinearDifferentialEqutionswithMeromorphicCoefficients

MEI Fang,LIU Zhang,ZENG Chunhua

(College of Science,Jiangxi Agricultural University,330046,Nanchang,PRC)

In the paper,We investigate the hyper-order of convergence of the distinct zeros of solutions of second order non-homogeneouslinear differential equtions with meromorphic coefficientsf″+Af′+Bf=F.When the coefficients satisfy some conditions,we obtain the precise estimates of the soutions.

meromorphic function;non-homogeneous linear differential equation;hyper-order of convergence of distinct zeros

2014-03-24;

2014-04-27

梅 芳(1972-)，女，江西九江人，硕士，副教授，目前从事应用数学方向的教学与研究。

2012年江西省教育厅教学改革研究项目(jxjg-12-4-13)。

1001-3679(2014)03-0281-03

O174.5

A