基于Simulink的四翼超混沌系统的仿真与分析

尹社会，王记昌

(河南工业职业技术学院，473000,河南,南阳)

基于Simulink的四翼超混沌系统的仿真与分析

尹社会，王记昌

(河南工业职业技术学院，473000,河南,南阳)

在一个四翼超混沌系统的微分数学模型基础上，利用Matlab软件和Simulink工具箱混合编程进行了仿真和模拟，通过改变控制参数的值，得到相应的结果变化情况，证明了该系统中存在分叉现象。在假设控制参数一致而稍微改动系统的初始条件，发现其动力学行为特性完全不一样，表明了系统对初值的极其敏感性。

超混沌系统；数值仿真；混沌；分叉

0 引言

Matlab/Simulink是一个进行动态系统建模、仿真和综合分析的集成软件包，功能强大。利用Simulink可以进行模块化建模，不仅可以显示具体环节的动态细节，还能呈现各部分(模块)之间的交互影响。由于四翼混沌系统比两翼混沌系统的动力学行为更复杂，因此把四翼混沌系统应用到保密通信中能使保密通信更安全、信息更难被破译。近年来对四翼混沌系统的构造与应用已成为国内外的研究热点[1-16]。本文在一个四翼超混沌系统的数学模型基础上，应用该软件包建立仿真模型，动态地分析系统中的分叉和混沌现象。

2003年Liu等构造了第一个四翼混沌系统，尽管被证明是假的四翼混沌系统，但却引起了人们对构造四翼混沌系统的兴趣。如Wang等构造了一个能产生三翼和四翼混沌吸引子的混沌系统，Dadras等构造了一个能两翼三翼和四翼混沌吸引子的混沌系统和一个能产生一翼两翼三翼和四翼混沌吸引子的混沌系统。由于超混沌系统有2个正的李雅普诺夫指数，比只有一个正的李雅普诺夫指数的混沌系统的动力学行为更丰富更复杂。因此有必要对四翼超混沌系统的动力学特性进行分析和研究。

2013年，黄沄[17]等引进了下面的一个四翼超混沌系统，该系统含有4个参数，其中3个方程中含有非线性乘积项。他们通过相图、平衡点以及Lyapunov指数谱分析了该系统的基本动力学特性，并实现了FPGA电路设计。但是该系统的Hopf分叉、Lyapunov维数、系统的最终界等未见有报道。因此有必要通过理论分析和数值计算等手段进一步讨论该系统的动力学行为。

1 系统模型及其动力学特性

四翼超混沌系统的数学模型如下[17]：

(1)

引理1：系统的Lyapunov指数之和等于相空间的时间平均散度。

2 Simulink建模与仿真

2.1Simulink建模与参数设置

根据微分数学模型建立系统的仿真模型如图2所示。在Simulink菜单下，通过Configuration Parameters设置参数：选择solver算法：ode45，最大步长为1e-6，仿真时间为200 s；其余通过元件编辑属性：a=3,b=9,c=4,k=8，设置积分器的初值为x=14,y=15,z=15,w=16。

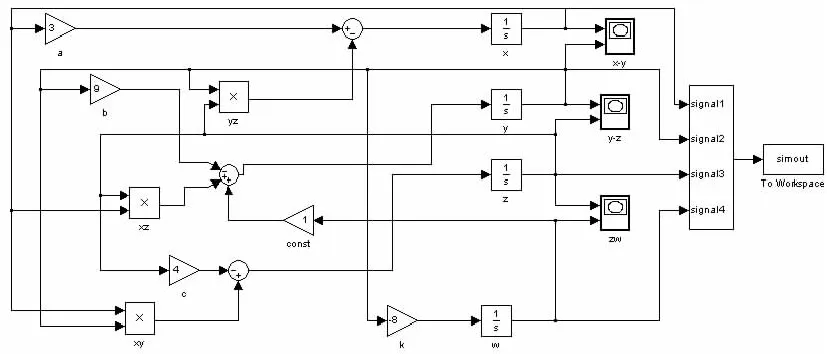
图2 基于Simulink的四翼超混沌系统仿真模型

2.2数值仿真结果分析

代入系统参数，在不同的控制参数和初始条件下分析系统的动力学行为特性。通过上一节建立的Simulink仿真模型，得到状态变量时间响应图(图3)、部分三维相图(图4)以及在部分平面内的投影图(图5)，通过改变初值也可以方便的验证该系统“蝴蝶效应”(图6)。

3 结论

对一个四翼超混沌系统进行了Simulink建模仿真并进行了研究，绘制了混沌系统的的各空间相图与平面投影相图，数值验证了混沌的“蝴蝶效应”。利用Matlab软件与Simulink仿真工具不仅可以获得许多重要的有效控制策略和仿真结果，而且为超混沌系统进一步的研究提供了便利。从上面的仿真可以看到随着控制参数和初始条件的变化而引起的系统行为特性变化情况。通过Simulink建模，探索了混沌系统中的分叉现象，动态地观察了系统运动过程。过程细节清楚，物理概念清晰。同时还可以看出，即使2个初始条件非常接近，系统的行为特性还是不一致的，最终的结果也是完全不一样的。

图3 状态变量时间响应图

图5 吸引子的二维相图

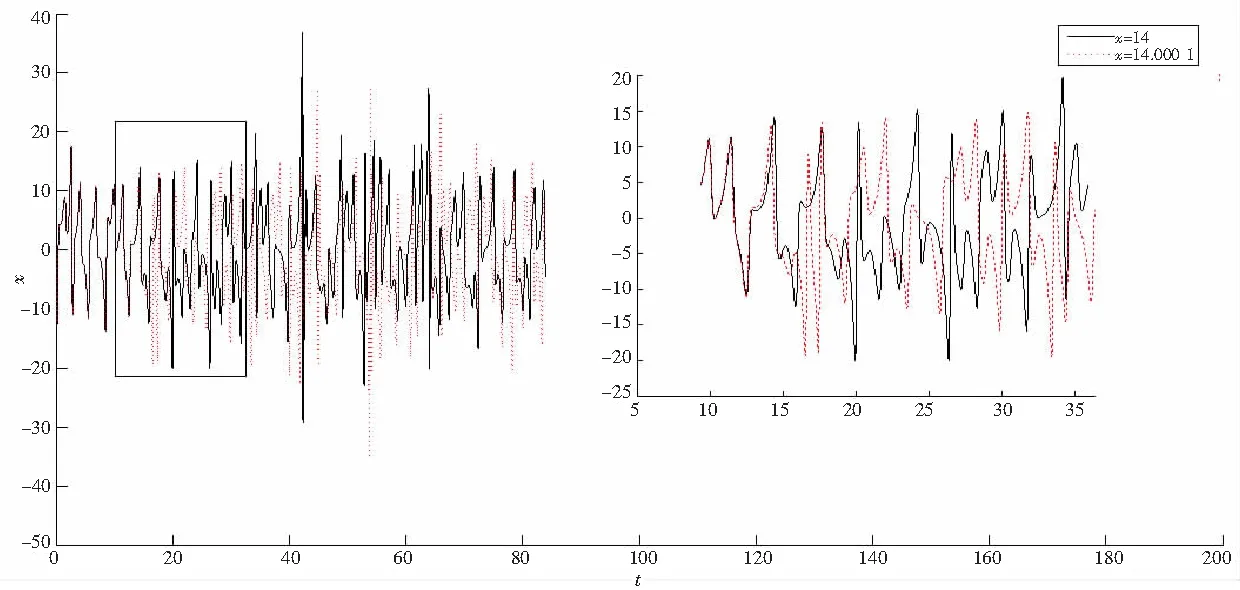
图6 x值的初值敏感性时间响应图

[1] 鲁池梅.一个四维四翼混沌系统及其电路实现[J].信息与电子工程,2011,9(2):229-233.

[2]王繁珍,齐国元,陈增强,等.一个四翼混沌吸引子[J].物理学报,2007,56(6):3137-3144.

[3]胡国四.一类具有四翼吸引子的超混沌系统[J].物理学报,2009,58(6):3734-3741.

[4]邓斌,王忠林,侯承玺.一个四翼混沌系统的设计与实现[J].济南大学学报(自然科学版),2010,24(4): 402-406.

[5]王忠林,邓斌,侯承玺.四翼liu混沌系统的设计与电路实现[J].山东大学学报(理学版),2010,45(11):43-46.

[6]邓斌,姚福安,王忠林,等.一个具有四翼吸引子的超混沌系统与电路实现[J].青岛科技大学学报(自然科学版),2010,31(6):622-626.

[7]王忠林,黄娜.一个三维四翼混沌系统的设计与FPGA实现[J].中国海洋大学学报,2010,40(12):131-134.

[8]朱雷,武花干.四翼蝴蝶Lü吸引子的电路设计与实现[J].电子器件,2011,34(1):66-69.

[9]满峰泉,许明清,王忠林,等.一个具有四翼吸引子的超混沌系统设计与实现[J].重庆邮电大学学报(自然科学版),2011,23(2):202-206.

[10]陈昌川.一种多翼超混沌系统及其FPGA实现[J].微电子学,2011,41(4):562-566.

[11]马文涛,赵芳玲.一种四翼混沌模型的扩展及其应用[J].陕西理工学院学报(自然科学版),2012,28(2):37-43.

[12]胥红星.一个多翼混沌系统的分析与同步[J].河南城建学院学报,2012,21(4):60-63.

[13]余飞,王春华,尹晋文,等.一个具有完全四翼形式的四维混沌系统[J].物理学报,2012,61(2):020506-10.

[14]孙克辉,刘璇,朱从旭.四翼超混沌系统的动力学特性分析及其电路实现[J].电路与系统学报,2013,18(1):285-289.

[15]屈双惠,容旭巍,吴淑花,等.一个四翼超混沌系统的电路实现及其同步控制[J].华中师范大学学报(自然科学版),2013,47(2):189-194.

[16]杜文举,余建宁,安新磊,等.一个新的四翼混沌系统的动力学分析[J].云南民族大学学报(自然科学版),2013,22(4):275-279.

[17]黄沄,张鹏,赵卫峰.一个新的四翼超混沌系统及其FPGA实现[J].西南大学学报(自然科学版),2013,35(6):127-130.

SimulationandAnalysisofaFour-WingHyperchaoticSystemBasedonSimulink

YIN Shehui,WANG Jichang

(Henan Polytechnic Institute,473000,Nanyang,Henan,PRC)

On the base of the mathematical model of four-wing hyperchaotic system,using Matlab and Simulink toolbox to simulate and changing the control parameters,we can prove the bifurcation exists in the system.And if we only change initial values,we can find dynamic behavior is significantly different,which shows the sensitivity of chaotic system to the initial conditions.

four-wing hyperchaotic system;simulation;chaotic;bifurcation

2014-03-25;

2014-04-24

尹社会(1979-)，男，河南沈丘人，讲师，研究方向为动力系统和物理实验教学等。

南阳市科技发展规划项目(2013GG048,2013RK013)。

1001-3679(2014)03-0284-04

O415.5

A