团体择优广义合作网络的度分布分析

张 野, 孔祥星

(1.长沙航空职业技术学院 培训与国际交流处, 长沙 410116;2.上海国际集团公司 博士后科研工作站, 上海 200041;3.中南大学 数学与统计学院, 长沙 410075;4.复旦大学 应用经济学博士后流动站, 上海 200433)



团体择优广义合作网络的度分布分析

张 野1,3, 孔祥星2,4*

(1.长沙航空职业技术学院 培训与国际交流处, 长沙 410116;2.上海国际集团公司 博士后科研工作站, 上海 200041;3.中南大学 数学与统计学院, 长沙 410075;4.复旦大学 应用经济学博士后流动站, 上海 200433)

将团体竞争的思想引入到合作网络的研究中, 提出了一个团体择优广义合作网络模型, 其中, 新加入的节点以团体择优概率选择已存在的节点形成一个含有T个节点完全图. 利用马尔可夫链的方法, 证明了网络的稳态度分布是存在的, 且得到了网络度分布的精确解析表达式, 并说明了此广义合作网络是一个标度指数γ=T+1的无标度网络.

复杂网络; 广义合作网络; 马氏链; 度分布; 无标度

从Watts和Strogatz[1]研究小世界网络与Barabasi和Albert[2]研究无标度网络开始, 复杂网络的结构和功能便成为众多学者广泛关注的问题. 社会合作网络(由节点和完全图组成, 其中, 每一个节点表示一个合作者, 完全图表示由节点所对应的合作者共同参与的项目)是一类很重要的复杂网络, 如在电影演员合作网络中, 每一名演员是一个合作者, 多名演员共同参与了一部电影的拍摄, 这里合作拍摄的电影就是一个合作项目. 科学家们对合作网络做了大量的实证和理论研究工作, 如电影演员合作网络[1], 科研合作网络[3-4], 友谊网络[5]等. 随着对社会合作网络研究的深入和对合作关系的推广, 学者们提出了广义合作网络的概念, 使合作网络的研究领域得到了扩大和延伸, 如生物系统网络[6-7], 软件合作网络[8], 菜系网络[9]等.

张培培等[10]构造了一个广义合作网络模型, 利用平均场方法分析了网络的度分布, 并讨论了网络的同类型, 群落层次及交连度等问题. 黄相森等[11]讨论了合作网络的分类问题. 赵清贵等[12]对广义合作网络模型的度分布进行了分析, 严格证明了网络的稳态度分布是存在的, 并得到了度分布的精确解析表达式. 雷敏[13]提出了一个项目所含合作者数为随机变量的广义合作网络模型, 得到了该模型度分布的精确解析表达式, 并说明了该广义合作网络不是无标度网络.

合作网络概念和模型的提出, 为研究现实的合作关系提供了一个新的视角. 在合作网络模型中, 每个完全图都含有一定数目(T个)的节点, 且在每个时刻都会有新节点加入到合作网络中, 它会以一定的方式(如随机选择, 择优选择或混合型)在网络中选择T-1个节点共同组成一个新的完全图. 在现有的合作网络模型中, 新节点在选择其它节点组成完全图时是逐个选取的. 在社会竞争日益激烈的情况下, 团队合作精神和竞争力显得更为重要,具备较强整体实力的团队才能获更多的发展机会. 本文将团队整体实力竞争的思想引入到广义合作网络的研究中, 基于文献[14]提出的团体择优思想提出了一个新的广义合作网络模型, 其中, 新节点在网络中选取T-1个节点时的概率是团体择优概率(即依赖于团体的度数之和). 通过节点度在网络演化过程中所满足的马尔可夫性, 用马氏链的方法和技巧对网络的度分布进行了严格的分析, 得到了度分布的精确解析表达式, 并说明了该网络是一个度指数γ=T+1的无标度网络.

1模型描述

团体择优广义合作网络模型的构造如下: 初始网络(在t=0时刻)G0是一个包含m0个节点的完全图, 每个时间步进行如下操作:

(I) 增长: 增加一个新节点,与网络中的T-1 (T≤m0+1)旧节点一起组成一个完全图;

(II) 团体择优: 新节点t(在时刻t加入网络的节点)在图Gt-1中选择T-1个旧节点的概率与它们的度数(节点度定义为节点参与完全图的数目)之和成正比, 然后把这T个节点相互连接成一个完全图, 进而得到网络Gt.

经过t时间步后得到网络Gt. 节点总数为Nt=m0+t≈t, 节点度数之和为Ht=Tt.

2度分布分析

令hi(t)表示节点i在时刻t的度数, 节点的瞬时度分布P(h,i,t)定义为:

P(h,i,t)=P{hi(t)=h},

网络的瞬时度分布P(h,t)定义为节点瞬时度分布的平均值

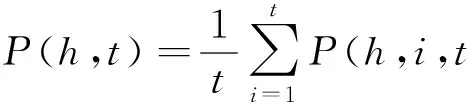
(1)

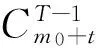
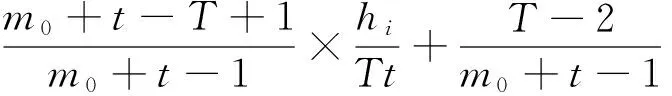
(2)

从而马氏链{hi(t)}的状态转移概率为:

P{hi(t)=l|hi(t-1)=h}=

(3)

由广义合作网络的特征,可知网络中节点度的最小值为1, 且每个时间步度数至多增加1. 对于团体择优广义合作网络的度分布可得如下引理1.

引理1在团体择优广义合作网络中, 瞬时度分布P(1,t)的极限(记为P(1))存在, 且与初始网络无关, 可得

(4)

证明度数为1的节点为那些刚加入网络的节点或加入网络后没有再参加过其它完全图的节点. 由P(1,t)的定义(1)式及转移概率(3)式, 得

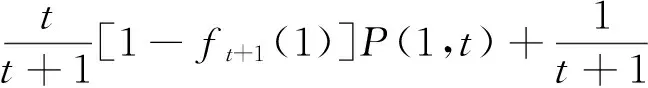
这是一个关于P(1,t)的一阶线性差分方程,其解为：

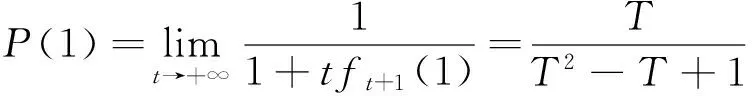
上面的引理1证明了团体择优广义合作网络的度分布P(1)是存在的,并求出了它的解析表达式.下面对度分布P(h) (h>1)的存在性和表达式问题进行分析.

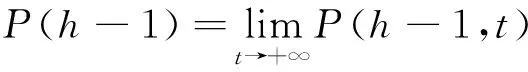
(5)

证明网络中度数为h的节点, 可能由那些度数为h-1的节点参与一个新完全图, 或由那些度数为h的节点不参与新完全图而得到. 可得

P(h,i,t+1)=P(h,i,t)[1-ft+1(h)]+

P(h-1,i,t)ft+1(h-1).

由P(h,t+1)的定义及P(h,t+1,t+1)=0, 可得

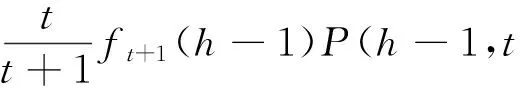
上述方程是一个关于P(h,t)的二阶线性差分方程,解此方程得

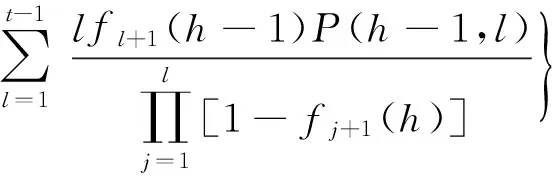
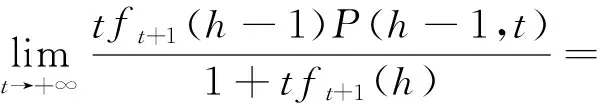
定理1团体择优广义合作网络的稳态度分布存在, 其度分布有如下的表达式:

(6)

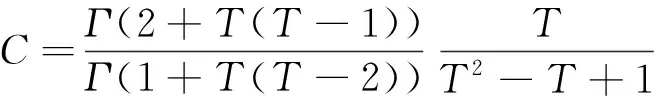
证明由引理1和引理2易知团体择优广义合作网络的稳态度分布是存在的. 由(4)和(5)式可递推得(6)式, 从而该网络是一个标度指数γ=T+1的无标度网络.

3总结

本文将团队竞争的思想引入到广义合作网络的研究中, 提出了一个团体择优的广义合作网络模型. 此处的团体择优概率是节点度的线性函数, 保持了BA模型中择优概率的线性原则. 由模型的演化规则,可得节点度{hi(t)}是一个马氏链, 并得到了它的初始分布和一步状态转移概率. 依据马氏链理论, 严格证明了该广义合作网络模型的稳态度分布是存在的, 并求出了节点度分布的精确解析表达式. 说明了该广义合作网络是一个标度指数γ=1+T的无标度网络.

在广义合作网络的研究中, 节点度的相关性是另外一个非常重要的特征, 它描述了一个节点在选择相连节点时对节点特征的偏好, 如果度数大的节点倾向于连接度数大的节点则称此网络为正相关或同类匹配的, 反之称网络为负相关或非同类匹配的. 对于节点度相关性的描述可通过条件概率P(k′|k)来描述, 表示一个度数为k的节点连接到度数为k′的节点的概率, 或通过邻居节点的平均度等方法来描述, 将在后续的工作中研究广义合作网络的节点度相关性问题.

[1] Watts D J,Strogatz S H. Collective dynamics of 'small-word' networks[J]. Nature, 1998, 393: 440-442.

[2] Barabasi A L,Albert R. Emergence of scaling in random networks[J].Science, 1999, 286: 509-512.

[3] Hajra K B,Sen P. Aging in citation network[J]. Physica A:Statistical Mechanics and its Applications, 2005, 346(1-2): 44-48.

[4] Ramasco J J, Dorogovtsev S N,Pastor-Satorras R. Self-organization of collaboration networks[J]. Physical Review E, 2004, 70(3): 036106, 1-10.

[5] Parker S L, Parker G R, Mccann J A. Opinion taking within friendship networks[J]. American Journal of Political Science, 2008,52(2): 412-420.

[6] Fell D A,Wagner A. The small world of metabolism[J]. Nature Biotechnology,2000, 18: 1121-1122.

[7] Chang S, Jiao X,Gong X Q,et al. Evolving model of amino acid networks[J].Physical Review E, 2008, 77(6): 061920,1-7.

[8] Myers C R. Software systems as complex networks: Structure, function, and evolvability of software collaboration graphs[J]. Physical Review E, 2003, 68(4): 046116, 1-15.

[9] 张培培, 侯 威, 何 阅, 等. 淮扬菜系的网络描述[J]. 复杂系统与复杂性科学,2005, 2(2): 49-53.

[10] 张培培, 何到阅, 周 涛. 一个描述合作网络顶点度分布的模型[J].物理学报, 2006, 55(1): 60-67.

[11] 黄相森, 张淑华. 基于合作网络的分类讨论[J]. 科技与生产, 2011,11(8): 141-144.

[12] 赵清贵, 孔祥星, 侯振挺. 简易广义合作网络度分布的稳定性[J]. 物理学报,2009, 58(10): 6682-6685.

[13] 雷 敏. 随机连接广义合作网络模型[J]. 数学理论与应用, 2012, 32(3): 94-98.

[14] Ye B, Hou Z Z,Kong X X. Scale-free network with variable scaling exponent[C]//2010 International Workshop on Chaos-Fractal Theory and its Applications, 2010, 400-403.

The degree distribution of generalized collaboration network wit group preferential attachment

ZHANG Ye1,3, KONG Xiangxing2,4

(1.Training and International Office, Changsha Aeronautical Vocational and Technical College, Changsha 410116；2.Postdoctoral Scientific Research Workstation, Shanghai International Group Co.Ltd. (SIG), Shanghai 200041;3.School of Mathematics and Statistics, Central South University, Changsha 410075;4.Postdoctoral Research Station for Applied Economics, Fudan University, Shanghai 200433)

Inspired by the idea of team competition, a generalized collaboration network with group preferential attachment is proposed, in which the new vertex will join a complete graph withT-1 vertices chosen from the existing network preferentially. Based on the techniques of Markov chain theory, the existence of the steady degree distribution is proved, and the expressions for the degree distribution are obtained. Theoretical results show that this generalized collaboration network is a scale free network with degree exponentγ=T+1.

complex networks; generalized collaboration network; Markov chain; degree distribution; scale free

2013-12-04.

国家自然科学基金项目(11071258,11101433).

1000-1190(2014)04-0483-04

N945

A

*通讯联系人. E-mail: xiangxingkong@gmail.com.