改进增强峭度图和增强包络谱在滚动轴承故障诊断上的应用

唐贵基，王晓龙，邓飞跃

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

滚动轴承是旋转机械中的重要组成零部件，其运行状态正常与否决定了整个系统的性能好坏。当轴承出现局部损伤或缺陷时，将产生周期性冲击振动，轻则使设备产生噪声、振动异常，重则损坏设备，因此对滚动轴承的故障诊断方法进行研究具有重要意义。共振解调分析是目前公认的滚动轴承故障诊断有效方法，该方法的关键在于能否准确获取中心频率、带宽等带通滤波参数。通常在选择共振频带时，需要测试人员根据经验对滤波参数进行设置，因此诊断结果难免会受到主观性判断的影响[1]。

早在1983年，Dwyer[2]就提出谱峭度(Spectral Kurtosis,SK)的概念，并将其作为功率谱密度的补充用于信号瞬态成分的提取，此后Antoni等[3-5]给出应用SK进行故障诊断的理论依据并先后提出基于短时傅里叶变换(STFT)的峭度图方法及基于有限冲击响应滤波器(FIR)的快速峭度图方法。然而,基于STFT和FIR的谱峭度法的抗干扰性均不够好，当被检测信号的信噪比较低时，其准确性将受限。为此文献[6]提出一种基于二进制小波包分解的增强峭度图法，该方法与快速峭度图相比，抗噪声干扰的鲁棒性更强，适合分析信噪比较低的故障信号。但由于增强峭度图的计算过程采用的是二进制频带划分方式，应用于轴承故障信号的共振频带筛选时，这种频带划分方式则显得不够细致，并且当共振频带中心位于1/2倍最大分析频率附近时，将会引起频率成分的泄漏。

为准确提取滚动轴承故障特征信息，在分析了增强峭度图方法的不足后，本文从避免频率成分泄漏这一角度出发，提出了基于谐波小波包分解的改进增强峭度图方法，用于故障信号最优分析频带的筛选，并将改进增强峭度图与增强包络谱方法相结合，用于对轴承故障进行精确诊断。滚动轴承内圈故障模拟、实测信号分析结果表明，本文提出的诊断新方法具有一定的可靠性和准确性。

1 基本原理介绍

1.1 谐波小波包分解

谐波小波的频域表达式为：

Wm，n(w)=

(1)

其中：m,n为尺度参数，w为频率。

时域表达式可通过式(1)的逆傅里叶变换得到：

(2)

设给定平移步长为k/(m-n),则式(2)变为：

wmn(t-k/(n-m))=

(3)

这就是分析频域带宽为2π(n-m)，分析时域中心为k/(n-m)的广义谐波小波的一般形式[7]。谐波小波同其它小波分解相似，在高频部分的频率分辨率相对较低，然而以谐波小波作为基函数系的谐波小波包分解却可以弥补这一不足，它可以对信号的高、低频部分同时进行分解，相比于其它小波包分解，谐波小波包可将信号无交叠、无泄漏地分解到互相独立的频带上，避免了其他频带成分对待分析频带成分的干扰[8]。通常情况下，谐波小波包也是以二进小波分解方式对频带进行划分的，但这种划分方式应用于滚动轴承故障信号的共振频带选择时略显粗糙，可能会造成某些重要频率成分的遗漏，为此本文在原分解方式基础上进行改进，采用一种相对连续的谐波小波分解方式对频带进行划分，令每层分解得到的子带个数(节点个数)与分解层数相等，这种划分方式使得每两个相邻层的分解结果只相差一个子频带。设s为谐波小波包分解层数，fh为最高分析频率，则各层子带的带宽fb及尺度参数m,n分别满足表达式：

fb=fh/s

(4)

(5)

改进后的谐波小波包分解可通过调整尺度参数m,n实现频带的精细分析及任意频带的精确提取。

1.2 改进的增强峭度图

基于谐波小波包分解的改进增强峭度图的具体实现过程如下所述：

(6)

(7)

计算完所有节点的峭度值后，将峭度值在二维平面上进行表示，得到的图像就是基于谐波小波包分解的改进增强峭度图，其横坐标代表频率，纵坐标代表分解层数，图像上的颜色深浅代表不同节点(对应不同的中心频率和带宽)处的峭度值大小。

1.3 增强包络谱

增强包络谱可通过自相关增强算法实现，该算法主要分为以下三个步骤[10]：

(1) 信号的自相关运算。设x(n)为原始离散信号，则原信号的自相关函数rxx(l)可以表示成：

rxx(l)=E[x(n)x*(n+l)]

(8)

其中:n=1,2,…,K，l=0,1,…,K-1，K为离散数据点个数，l为时间延迟，E[·]为数学期望，x*(·)为x(·)的共轭。

(2) 求取自相关包络谱。通过Hilbert变换得到自相关函数rxx(l)的包络Rxx(l)，然后对Rxx(l)做频谱分析得到自相关包络谱P(f)。

(3) 求取增强包络谱。在此，首先定义扩展的Shannon熵函数，表达式如下：

M(x)=H(x)log2H(x)

(9)

(10)

其中:i=1,2,…,n，n为自相关包络谱的离散数据点个数，u为标准差，表达式如下：

(11)

自相关包络谱通过扩展熵函数运算后，幅值大于u的成分得到增强，而幅值小于u的成分则被削弱。

2 故障诊断流程

为弥补快速峭度图对信号异常值敏感、容易受噪声影响等缺陷，文献[6]提出了增强峭度图方法，利用增强峭度图得到小波包分解最优节点，通过最优节点系数重构信号并进行包络谱分析，可以顺利提取出轴承故障特征信息。但是在计算增强峭度图的过程中，由于频带划分比较粗糙，存在频率成分泄漏的隐患，而本文提出的基于谐波小波包分解的改进增强峭度图方法却可以更细致的对信号频带进行刻画，能够有效避免重要频率成分的泄漏。

原信号通过最优节点系数重构后，虽然一定程度上可以抑制噪声的干扰，提高信号的信噪比，但是重构信号的带内残余噪声却不能被有效消除，然而通过信号的自相关增强运算，却可以达到减少频带内部噪声的目的。由于调幅信号的自相关函数仍是调幅信号，调频信号的频率调制信息可通过自相关运算转化为幅值调制信息，调幅调频信号的自相关运算结果仍是幅值调制及频率调制的，所以无论信号是调幅信号、调频信号还是调幅调频信号，它们的调制特征都可以通过对其自相关函数进行包络解调来提取[11]。为此，本文将改进增强峭度图与自相关增强算法相结合，提出了基于改进增强峭度图和增强包络谱的滚动轴承故障诊断新方法，具体流程如下：

(1) 设定谐波小波包的分解层数。为使最小带宽的子带信号也能够保留足够的故障特征信息，本文认为，最大分解层上得到的子带的带宽应大于内圈故障特征频率理论值的2倍，由此可以确定谐波小波包分解层数的上限，只要不超过上限分解层数，设定的分解层数可根据实际情况做适当调整。

(2) 计算信号的改进增强峭度图，确定最大峭度值节点的位置，通过该处节点的系数重构信号。

(3) 计算重构信号的增强包络谱。

(4) 通过增强包络谱中幅值明显的频率成分与故障特征频率理论值的对比分析进行故障诊断。

3 内圈故障模拟信号分析

利用文献[12]中提出的滚动轴承内圈故障仿真模型来验证强噪声干扰下本文提出的诊断方法的有效性。其中，采样频率fs=12 000Hz，采样点数N=12 000点，轴承所在工作轴转频fr=25 Hz，内圈故障特征频率fi=110 Hz，共振频率fd=3 000 Hz，添加的高斯白噪声信噪比SNR=-15 dB。故障模拟信号及加噪后的故障模拟信号分别如图1(a)、图1(b)所示。

图1 故障模拟信号及加噪后的故障模拟信号

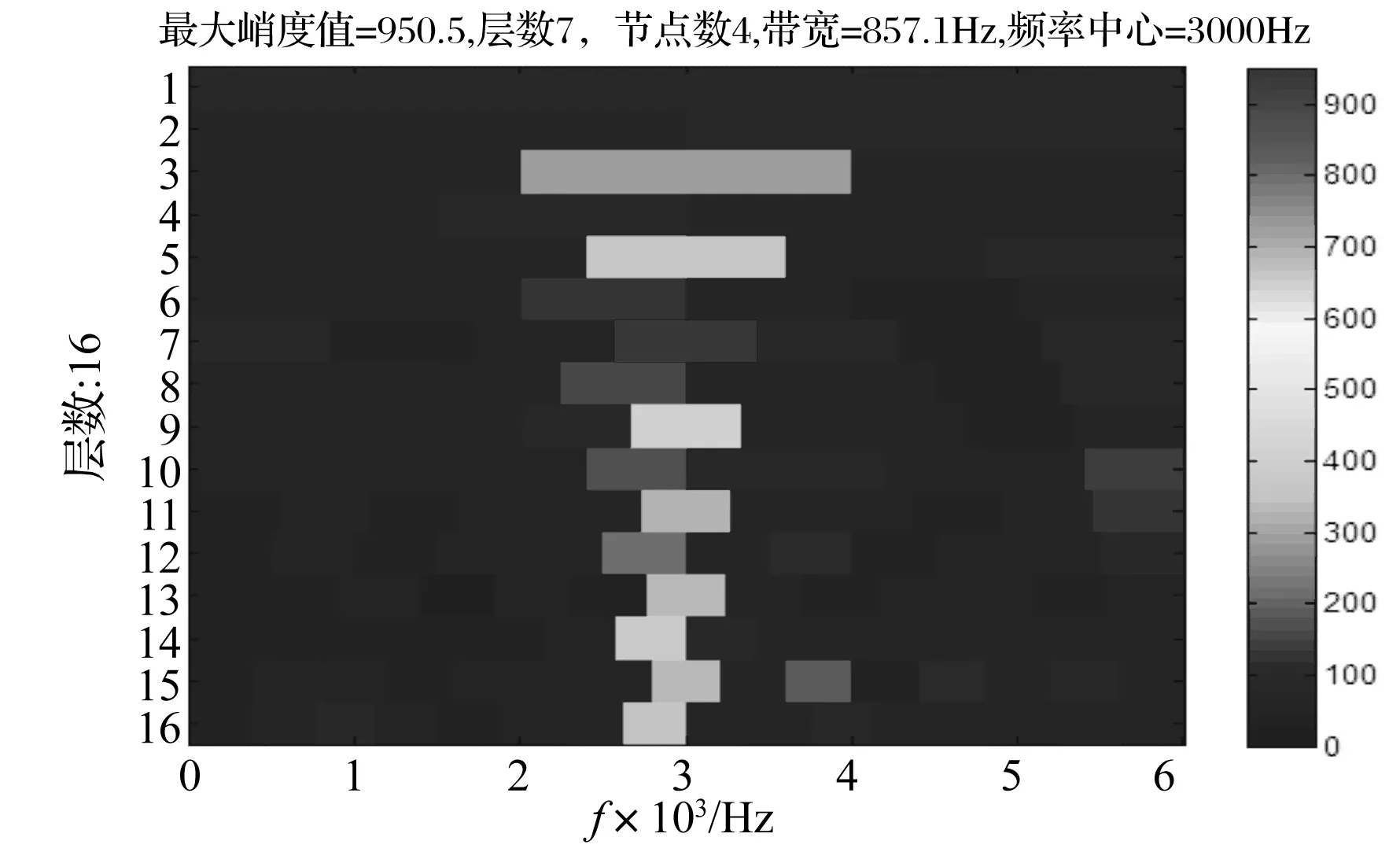
图2 加噪故障模拟信号的改进增强峭度图

设定谐波小波包分解层数为16，计算得到加噪故障模拟信号的改进增强峭度图(如图2所示)，通过改进增强峭度图可知第7层第4个节点的峭度值最大，该节点对应的子频带带宽为857.1 Hz、频率中心为3 000 Hz，由此可知利用改进增强峭度图准确的筛选出了故障信号的共振频带中心，利用该最优节点的谐波小波包系数进行信号重构并做增强包络谱分析，结果如图3所示。重构信号的增强包络谱中，内圈故障特征频率及其二倍频、三倍频、四倍频等一系列频率成分处的谱线比较突出，并且能够找到转频成分及特征频率的转频调制边带。图4是对重构信号直接做包络谱分析的运算结果，虽然在包络谱中，特征频率及其倍频成分处的谱线幅值也比较明显，但是由于背景噪声干扰严重，转频及特征频率的转频调制边带成分均被噪声所淹没。通过对比可以发现，基于自相关增强算法得到的增强包络谱能够有效抑制信号的带内噪声干扰、提高信噪比，重构信号的增强包络谱分析结果要比包络谱分析结果更理想。

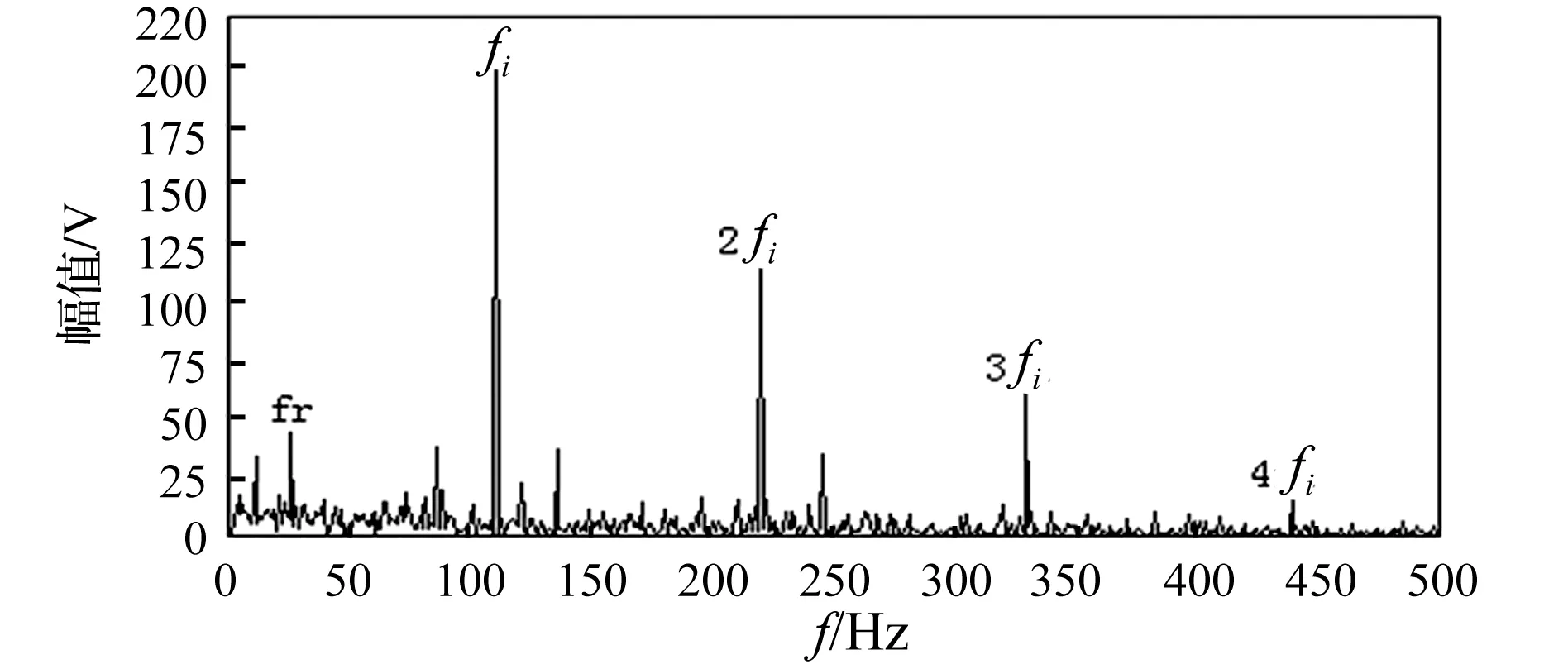
图3 重构信号的增强包络谱

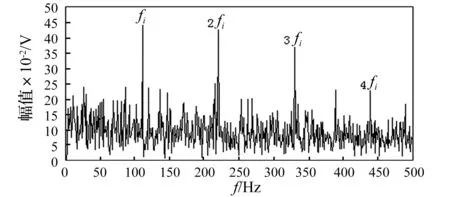
图4 重构信号的包络谱

下面利用增强峭度图结合包络谱的方法以及传统的直接求取包络谱的方法分别对加噪内圈故障模拟信号进行分析。由于改进增强峭度图的最大分解层数为16，即最多可获得16个子频带，为进行对比说明，设定增强峭度图的最大分解层数为4，分析结果同样最多可得到16个子频带。

首先计算加噪故障模拟信号的增强峭度图，结果如图5所示，增强峭度图中第4层第8个节点的峭度值最大，该节点对应的子带带宽为375 Hz、频带中心为2 812.5 Hz，由此可知增强峭度图并没有准确检测到信号的共振频带中心。由于模拟信号的共振频率(3 000 Hz)等于1/2倍最高分析频率(6 000 Hz)，而增强峭度图计算时采用的是相对粗糙的二进制频带划分方式，因此无论最大分解层数设定成多少，都无法正确检测到共振频带的中心。以3 000 Hz为中心、110 Hz为间隔的边频成分将被分解到两个相邻的子频带中去，与准确筛选出共振频率中心时的情况相比，此时最优节点的重构信号所包含的特征频率信息将有所减少，与故障特征相关的频率成分存在一定的泄漏，这种泄漏也必然会对后续分析结果造成不利影响。利用第4层第8个节点(最优节点)的小波包系数重构信号并做进一步包络谱分析，结果如图6所示，分析后可以发现，包络谱中仅在故障特征频率及其二倍频处谱线幅值较高，并且存在较多噪声干扰成分。对加噪故障模拟信号直接做包络谱分析，结果如图7所示，由于原信号中噪声干扰严重，包络谱中没有发现明显的故障特征相关谱线，从而无法提取到有用的特征频率信息。

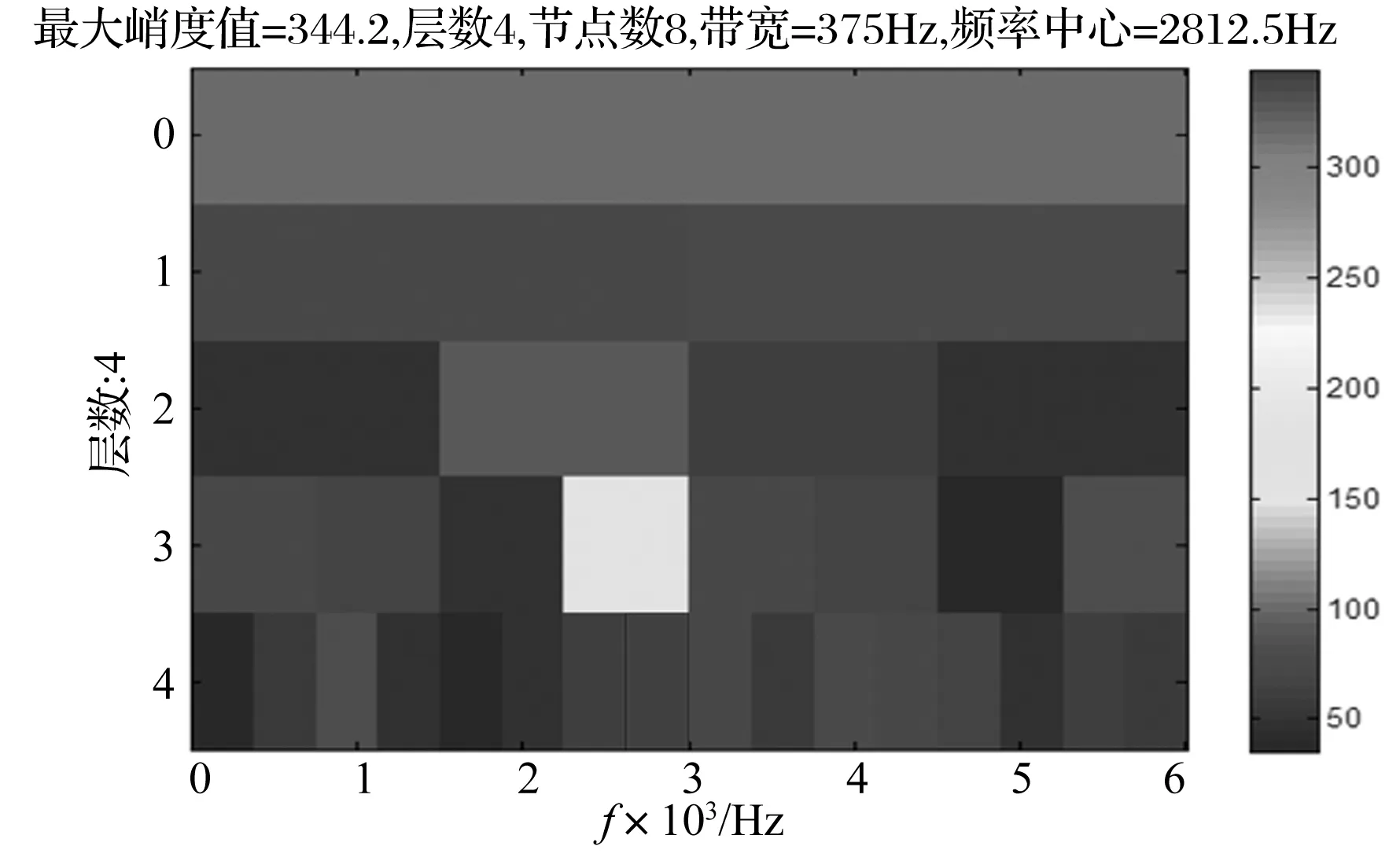
图5 加噪故障模拟信号的增强峭度图

图6 重构信号的包络谱

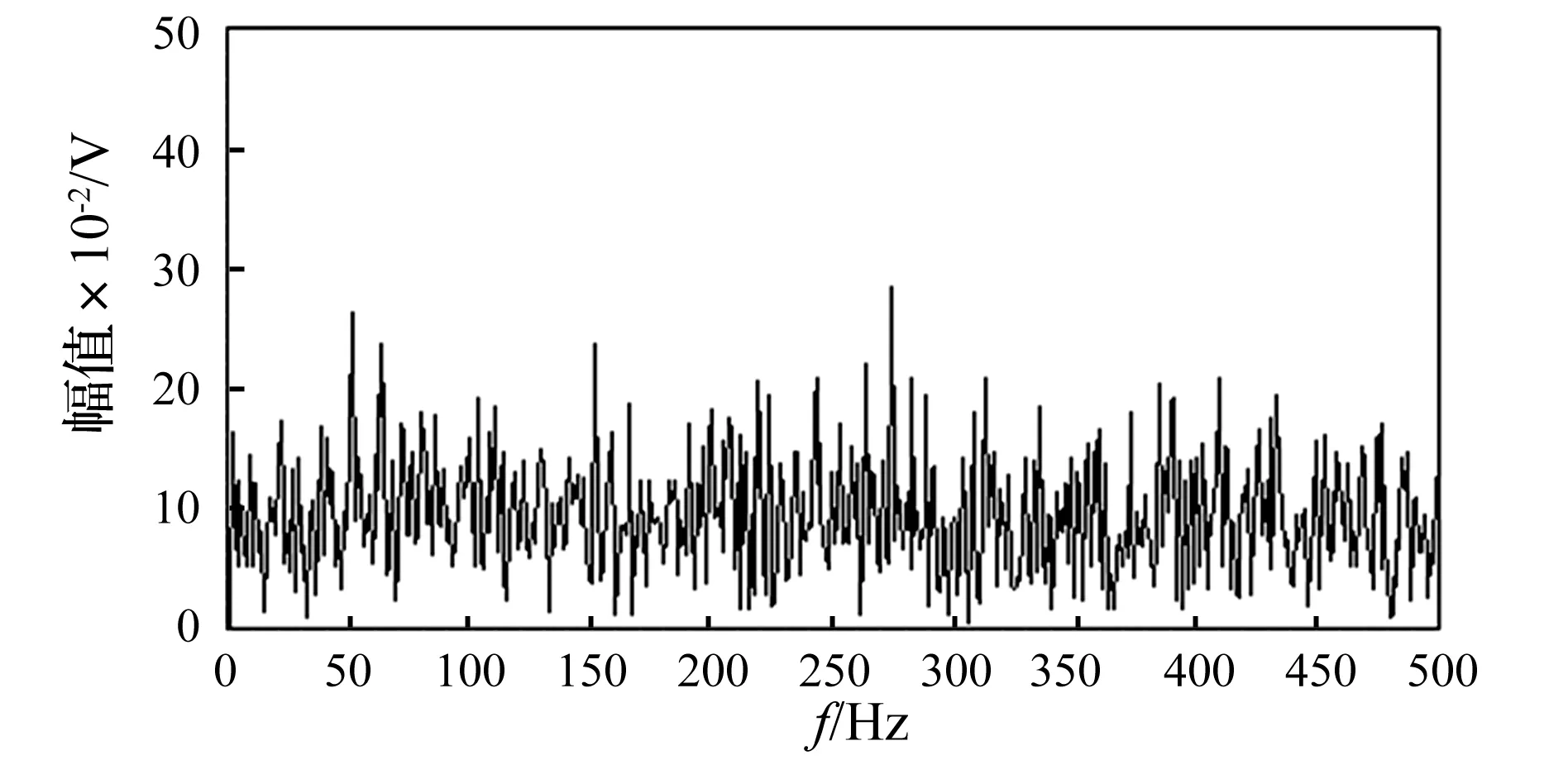
图7 加噪故障模拟信号的包络谱

通过对加噪内圈故障模拟信号进行分析，验证了基于改进增强峭度图和增强包络谱的滚动轴承故障诊断方法的准确性，并且与增强峭度图结合包络谱的方法以及直接求取包络谱的分析方法进行了对比，结果表明本文提出的方法可获得更理想的分析效果。

4 内圈故障实测信号分析

为进一步验证新方法在滚动轴承实际故障诊断应用上的可靠性，对美国Case Western Reserve大学滚动轴承数据中心的公开数据进行分析。本文采用的数据是驱动端SKF6205-2RS深沟球轴承内圈故障数据，内圈损伤为电火花加工的单点损伤，损伤点直径为0.533 4 mm。其中，轴承节径39 mm，滚动体个数9个，滚动体直径7.938 mm，接触角0°，采样频率fs=12 000 Hz，分析点数N=24 000点，电机轴转频fr=29.95 Hz，理论计算得到的轴承内圈故障特征频率fi=162.19 Hz。通过加速度传感器测得的原始信号时域波形及谱图分别如图8(a)、图8(b)所示，时域波形中出现冲击性成分，但是规律性不够明显，无法准确了解信号的故障特征信息，频谱成分丰富，存在多个共振频带，但与特征频率相关的谱线并不明显，仅通过时域波形及频谱不能准确判断出轴承的损伤位置。

图8 原始信号的时域波形及频谱

利用本文提出的诊断方法对原始信号进行分析，设定谐波小波包分解层数为16，计算得到原始信号的改进增强峭度图，结果如图9所示。改进增强峭度图中第5层第3个节点的峭度值最大，对应频率中心为3 000 Hz、带宽为1 200 Hz的子频带，利用最优节点的谐波小波包系数重构信号，并进行增强包络谱分析，结果如图10所示。图10中电机轴转频及其二倍频、内圈故障特征频率及其二倍频三倍频等一系列频率成分处的峰值谱线均比较明显，由此可以断定轴承内圈存在局部缺陷，诊断结果与实际情况相符。为进行对比，直接利用包络谱对重构信号进行分析，结果如图11所示。虽然在包络谱中也可以找到对应内圈故障特征频率及其二倍频成分的谱线，但却没有增强包络谱的分析结果那样明显，重构信号的包络谱诊断结果与增强包络谱诊断结果相比具有一定的差距。

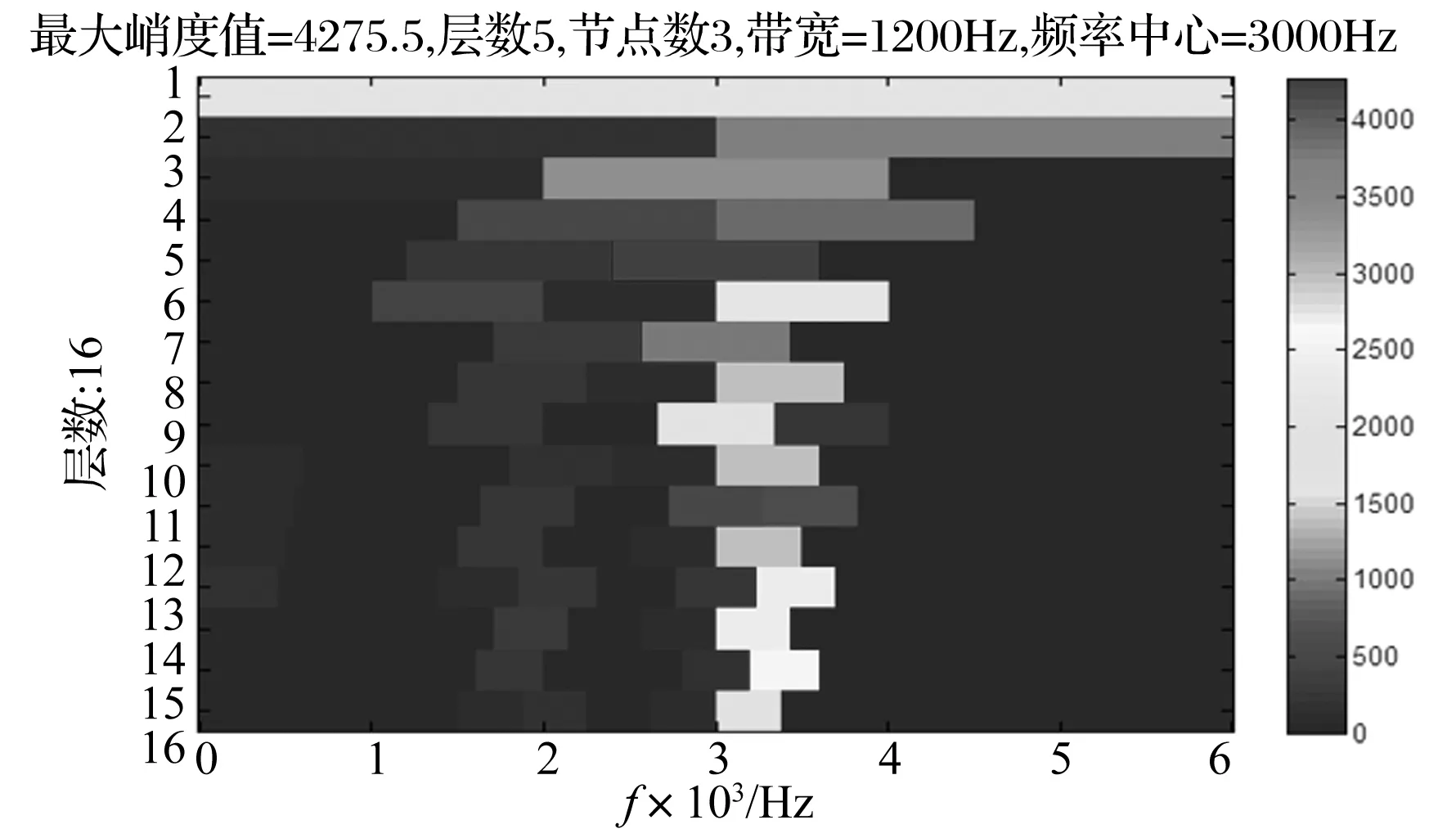
图9 原始信号的改进增强峭度图

图10 重构信号的增强包络谱

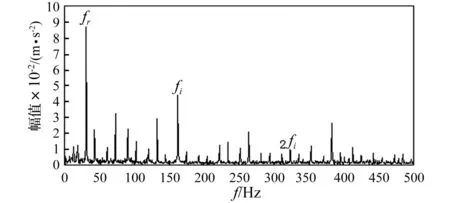
图11 重构信号的包络谱

下面利用增强峭度图结合包络谱的方法以及直接求取包络谱的方法分别对原始信号进行分析，设定最大分解层数为4，得到原始信号的增强峭度图如图12所示。增强峭度图中第3层第5个节点为最优节点，对应的频带带宽为750 Hz、频带中心为3 375 Hz，利用该节点处小波包系数重构信号并做包络谱分析，结果如图13所示，而对原信号直接做包络谱分析得到的结果如图14所示。经过对比可以发现，重构信号的包络谱分析结果和原信号的包络谱分析结果相差不大，图13和图14中，仅在162 Hz频率成分处存在一个谱峰，对应轴承内圈故障特征频率，但是谱线幅值不够突出，并且也找不到特征频率的倍频成分，诊断效果一般。

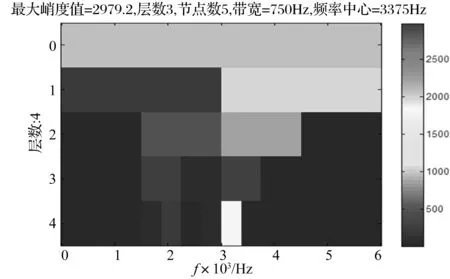
图12 原始信号的增强峭度图

图13 重构信号的包络谱

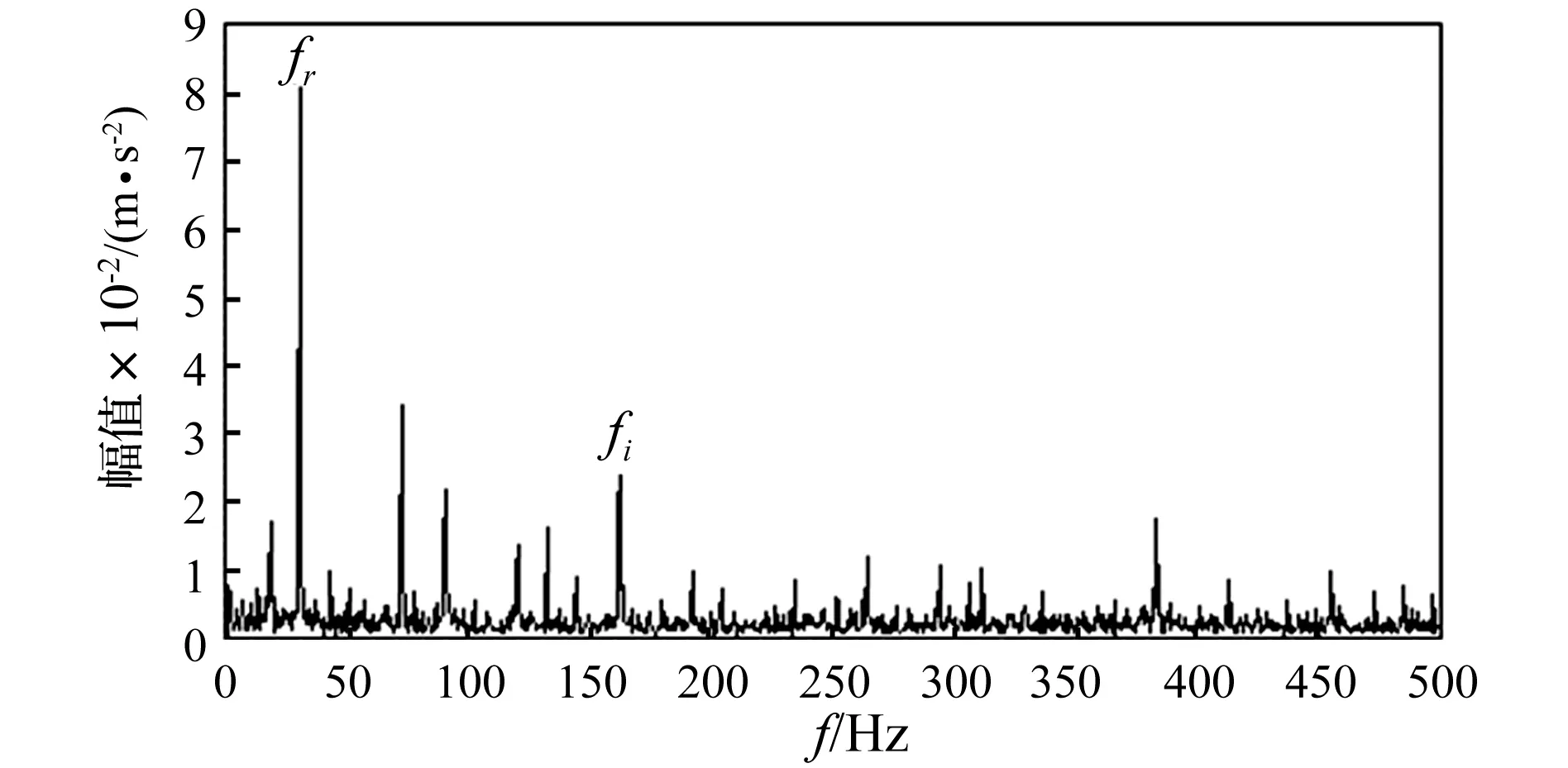
图14 原始信号的包络谱

通过分析实测信号，验证了本文提出的诊断方法在实际轴承故障诊断应用上的有效性，虽然基于改进增强峭度图结合增强包络谱的方法、增强峭度图结合包络谱的方法以及直接求取包络谱的方法均能顺利提取出故障特征频率信息，但对比后可以发现，本文提出的方法的分析效果更加明显，具有一定的优势。

5 结 论

提出了基于改进增强峭度图和增强包络谱的滚动轴承故障诊断新方法，轴承内圈故障模拟与实测信号的分析结果表明：

(1) 本文提出的基于谐波小波包分解的改进增强峭度图对频带的划分更加精细，并且受噪声影响较小，在一定程度上能够提高共振频带中心的选择精度，更有效的筛选出故障信号的最佳分析频带。

(2) 基于自相关增强算法的增强包络谱可有效抑制信号的带内噪声干扰，更有利于故障信息的提取。

(3) 结合改进增强峭度图和增强包络谱的滚动轴承故障诊断方法可准确提取出轴承故障特征频率信息，实现滚动轴承故障的精确诊断。

[1] 胡爱军，马万里，唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报，2012，32(11)：106-111.

HU Ai-jun,MA Wan-li,TANG Gui-ji.Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11): 106-111.

[2] Dwyer R F. Detection of non-gaussian signals by frequency domain kurtosis estimation[C]//Acoustics, Speech, and Signal Processing .Boston: IEEE International Conference on ICASSP,1983:607-610.

[3] Antoni J.The spectral kurtosis: A useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307.

[4] Antoni J, Randall R B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical Systems and Signal Processing, 2006,20(2):308-331.

[5] Antoni J.Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.

[6] Wang D, Tse P W, Tsui K L. An enhanced kurtogram method for fault diagnosis of rolling element bearings [J]. Mechanical Systems and Signal Processing,2013,35(1):176-199.

[7] 王胜春，韩捷，李志农，等.谐波小波包自适应分解在故障诊断中的应用[J].农业机械学报，2007，38(10)：174-177.

WANG Sheng-chun,HAN Jie,LI Zhi-nong,et al.Adaptive harmonic wavelet packet transform and its application to machine fault diagnosis[J].Transactions of the Chinese Society for Agricultural Machinery,2007,38(10):174-177.

[8] 王冬云.转子-轴承故障诊断方法研究[D].秦皇岛：燕山大学，2012.

[9] Marple S L.Computing the discrete-time analytic'' signal via FFT [J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2600-2603.

[10] Su Wen-sheng, Wang Feng-tao, Zhu Hong, et al. Rolling element bearing faults diagnosis based on optimal morlet wavelet filter and autocorrelation enhancement [J]. Mechanical Systems and Signal Processing,2010,24(5):1458-1472.

[11] 何威，江志农.时延自相关解调频原理及其在齿轮故障诊断中的应用[J].振动与冲击，2009，28(9)：195-199.

HE Wei,JIANG Zhi-nong.Frequency demodulation based on delayed autocorrelation and its applicationin gear fault diagnosis[J].Journal of Vibration and Shock, 2009, 28(9): 195-199.

[12] 周福昌.基于循环平稳信号处理的滚动轴承故障诊断方法研究[D].上海：上海交通大学，2006.