汽轮机座缸式轴承振动影响因素研究

高庆水, 刘 石, 张 楚

(广东电网公司 电力科学研究院,广州 510080)

大型汽轮机低压缸两侧轴承座有落地式和座缸式两种。座缸式轴承位于排汽缸扩压器洼窝中，转子和汽缸自重、真空载荷等通过轴承座传递到汽缸壳体，再经汽缸下部裙部支撑传递到基础上。这类机组轴系短，结构紧凑，在大型汽轮机上得到广泛应用。然而近年来很多机组座缸式轴承振动较大[1-2]，还出现了轴承振动比转轴振动大的异常现象。某台1 000 MW汽轮机台板和地基振动小于0.015 mm，而轴承振动达到0.044 mm，低压缸振动达到0.080 mm，异常振动严重影响了机组安全运行。

与落地式轴承相比，座缸式轴承支撑刚度较小，缸体变形等因素对支撑刚度影响较大[3-6]，振动分析时需要考虑转子-轴承-支撑系统耦合特性[7]。模态综合法[8-10]和阻抗匹配法[11]是两种常用的耦合分析方法。这2种方法将基础视为由多个集中质量块所组成的复杂结构，经模态分析后按相应准则组合为整体系统。汽轮发电机组基础振动较小，可以将基础影响用轴承座参振质量和支撑刚度来表示[12]，总体刚度由支撑刚度和油膜刚度串联构成。这种模型比较简单，不考虑油膜交叉刚度特性，也不考虑支撑刚度对系统等效阻尼的影响。

本文将轴承油膜特性用刚度、阻尼系数来表示，考虑支撑影响后建立了轴承-支撑系统等效动力模型，研究了某大型汽轮机低压转子振动特性和影响因素，对实际振动故障进行了综合分析。

1 支撑系统影响等效分析模型

图1给出了转子-轴承-支撑系统模型。油膜特性用刚度、阻尼系数表示，汽缸支撑用轴承座质量和支撑刚度来反映。轴承座运动方程为:

(1)

式中:m2为轴承座参振质量；kij,cij,i,j=x,y为油膜刚度和阻尼系数；kx,ky为水平和垂直支撑刚度；x1,2,y1,2为轴颈和轴承座水平和垂直位移。

图1 支撑系统分析模型

频率为ω的不平衡力激励下系统响应为：

x1,2=X1,2eiωt,y1,2=Y1,2eiωt

(2)

式中:X1,2,Y1,2为轴颈和轴承座振动位移幅值。

将式(2)代入式(1)得

(3)

由式(3)可得

(4)

式中:αij为轴振和瓦振之间的关系系数。

轴颈受到的油膜力fx,y为

(5)

令fx,y=Fx,yeiωt，Fx,y为油膜力幅值，将式(2)代入式(5)得

(6)

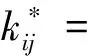
i,j=x,y

(7)

从上式可见，支撑刚度对系统等效刚度和等效阻尼都会产生影响。

2 支撑刚度对轴承动力特性影响分析

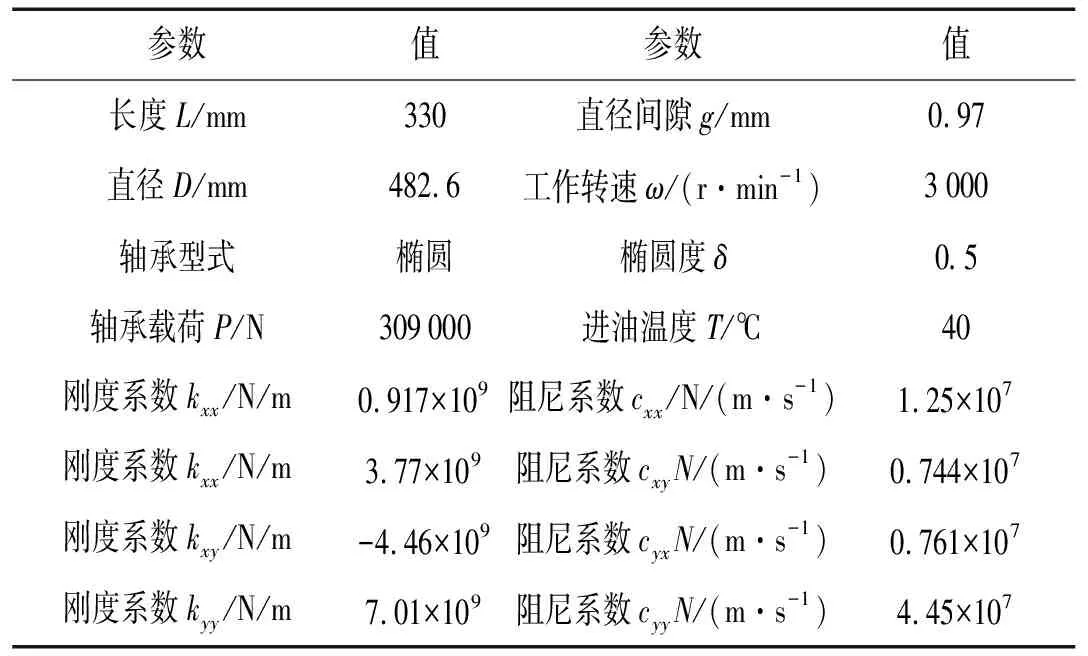
表1 轴承参数

图2 等效刚度和阻尼系数随支撑刚度变化情况

图2给出了系统等效刚度和阻尼系数随支撑刚度变化情况，支撑刚度对系统等效刚度和等效阻尼系数都会产生较大影响。支撑刚度大于1.5×1010N/m后，支撑刚度对系统等效刚度和阻尼的影响较小；支撑刚度小于1.5×1010N/m时，随着支撑刚度的降低，系统等效刚度和阻尼系数幅值下降很快，垂直和水平等效主刚度甚至变为负，这将对转子-轴承系统动力特性产生很大影响，轴承座振动将会很大。

计算和实测表明[3-6]，大型汽轮机组低压缸刚度在109N/m～1010N/m之间。对于本例而言，正好处于支撑刚度影响敏感区内。

3 某大型汽轮机低压转子振动分析

3.1 数学模型

图3给出了某大型汽轮机组转子-轴承系统动力学分析模型。高压转子两侧轴承为落地式，可不考虑支撑刚度影响。包含轴承油膜各向异性情况下的转子—轴承系统动力学方程为[12]:

图3 转子-轴承系统动力学模型

(8)

式中:M1、K1和G1为整体质量矩阵、刚度矩阵和回转矩阵[12]；

cij、kij为考虑支撑刚度影响后整体油膜等效阻尼和刚度矩阵；

U1,U2为系统位移向量

U1={x1θy1x2θy2…xnθyn}T

U2={y1-θx1y2-θx2…ynθxn}T

Q为不平衡力向量

(9)

式中:{Qc,s}为不平衡力向量中余弦和正弦分量值。设

(10)

式中:A1,A2,B1,B2为不平衡响应中余弦和正弦量值。

将式(9)和(10)代入式(8)，得

(11)

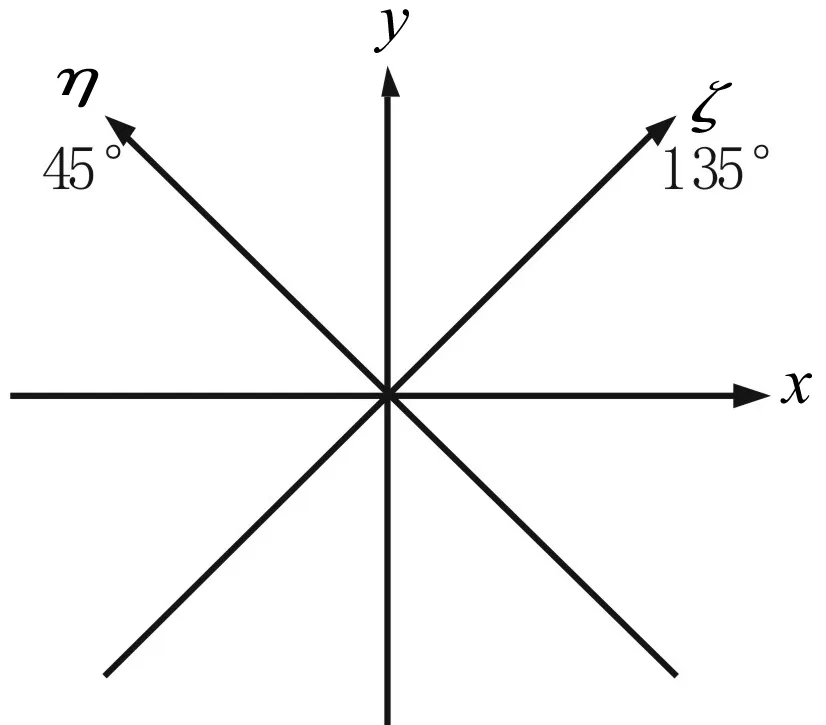
图4 轴振传感器坐标变换示意图

求出转轴绝对振动X1,Y1后，代入式(4)可求得轴承座振动X2,Y2，两者相减可以求得轴相对振动X3,Y3。

汽轮机轴振探头通常安装在如图4所示的45°和135°方向，而轴承座振动探头通常安装在垂直和水平方向上，可以通过坐标变换将其转换到同一坐标系下分析。设轴振坐标为ξ,η，该坐标下的振动与垂直和水平振动之间的关系为:

(13)

低压转子第3阶临界转速通常远高于工作转速，不平衡响应分析可以只考虑前两阶模态影响。计算时在低压转子两端末级叶轮处设置一组力偶，在中间叶轮处设置一组力。

3.2 支撑刚度对升速过程中振动影响分析

图5给出了不同支撑刚度下#3轴承轴绝对振动随转速变化情况。垂直和水平振动特性相似，现以水平轴振为例分析如下：

(1) 支撑刚度为1×1010N/m时，计算转速范围内没有出现共振峰值，升速过程中振动较小。

(2) 随着支撑刚度的降低，临界转速降低。支撑刚度降到2×109N/m时，临界转速已经下降到3 000 r/min以内。两个共振峰值所对应转速分别为转子第1阶和第2阶临界转速。

(3) 支撑刚度降到1.2×109N/m时，临界转速进一步降低，共振转速下不仅幅值大，而且共振峰较尖。在支撑弹性作用下系统等效阻尼减小，对共振峰值的抑制作用减弱。

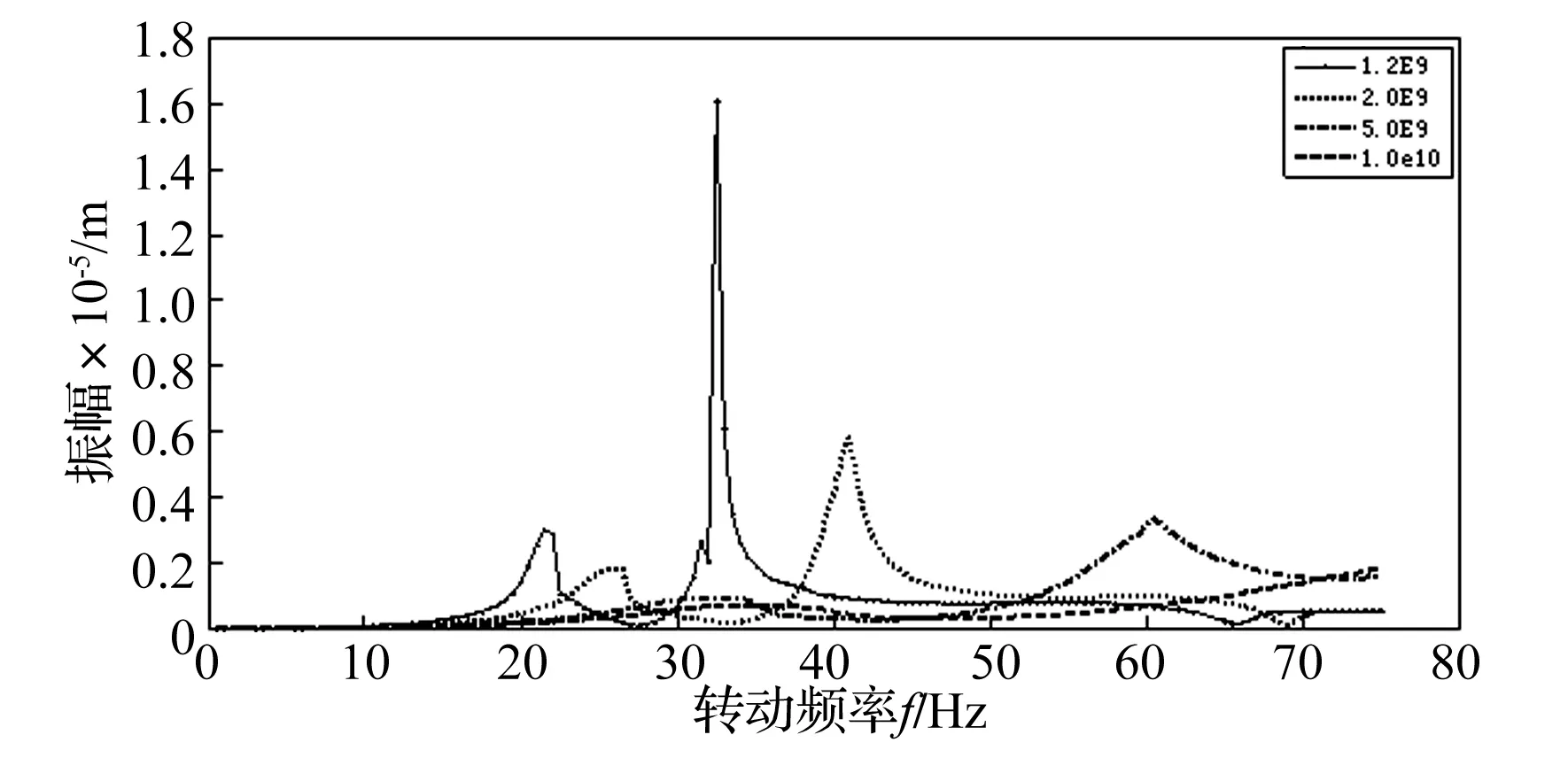
图5 不同支撑刚度下转轴振动随转速变化情况

3.3 不同支撑刚度下轴振/瓦振之间的幅值关系

图6给出了不同支撑刚度下轴振和瓦振随转速变化情况。不同支撑刚度下振动特性不同，轴振/瓦振关系差异较大。支撑刚度大时，升速过程中瓦振较小，轴振较大，绝对轴振和相对轴振近似相等。支撑刚度小时，升速过程中相对轴振较小，瓦振很大，绝对轴振和瓦振近似相等。

不同支撑刚度下，绝对轴振都能够较为准确地反映转子实际振动情况。对于低压转子而言，只监测相对轴振并不合理。

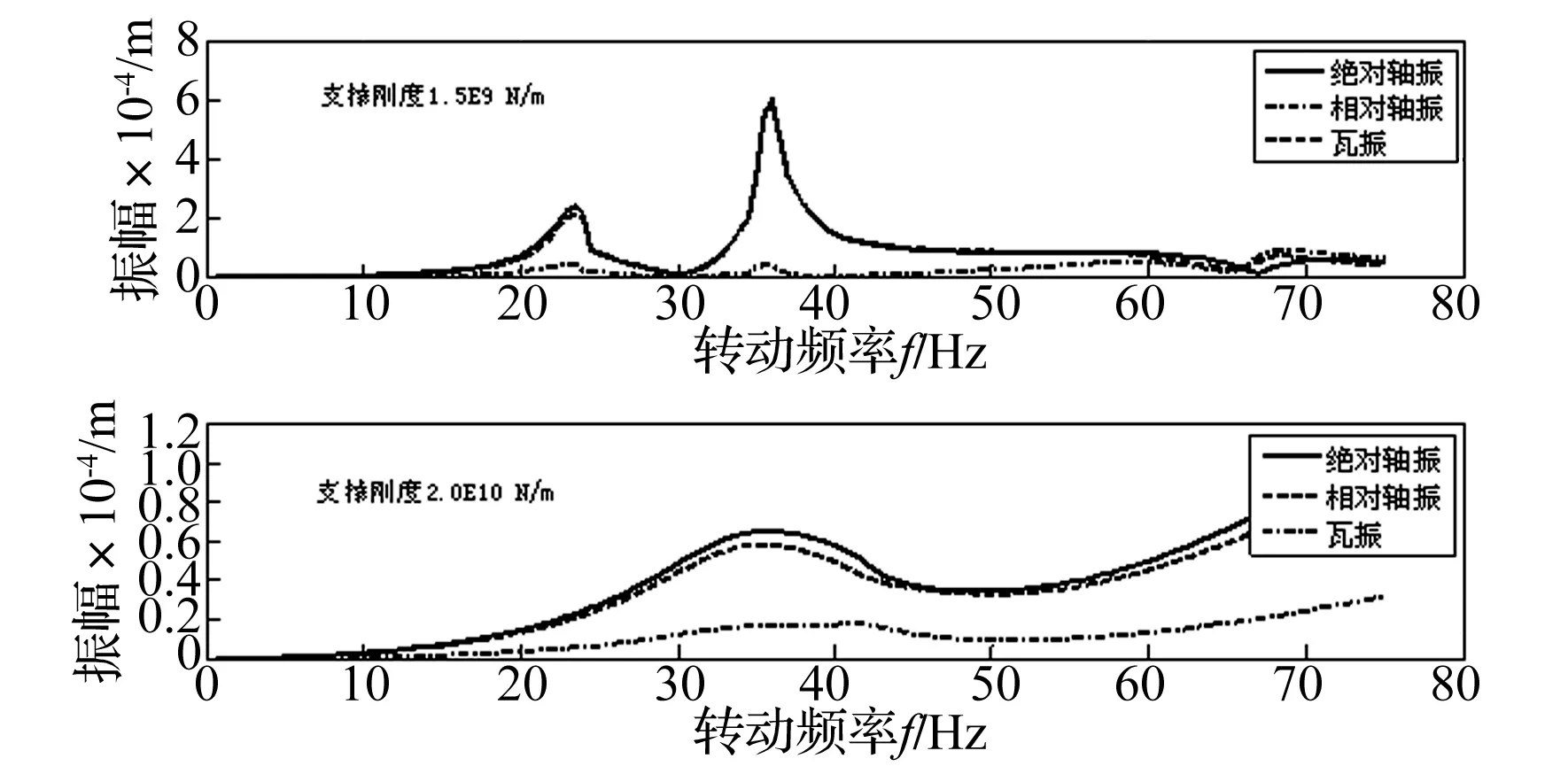
图6 不同支撑刚度下轴振和瓦振随转速变化情况

3.4 不同支撑刚度下轴振/瓦振之间的相位关系

大量观点认为，轴振和瓦振都反映了轴承振动情况，其相位应该相近。图7给出了不同支撑刚度下轴振、瓦振相位随转速变化情况。受支撑刚度影响，两者之间的相位关系实际上比较复杂。

图7 不同支撑刚度下轴振和瓦振之间的相位关系

(1) 支撑刚度小时，升速过程中绝对轴振和瓦振相位基本相同，相对轴振和瓦振相位相差了60°～150°；

(2) 支撑刚度大时，升速过程中绝对轴振和相对轴振相位基本相同，轴振和瓦振相位相差了约50°。

4 大型汽轮机组实际振动分析

某台1000 MW大型汽轮机组轴系由高、中压转子和两个低压转子组成。高、中压转子为落地轴承，低压转子为座缸式轴承。实测表明，3 000 r/min下低压转子两侧轴承座振动达到45 μm ～50 μm，处于合格边缘，但是轴振优秀，转轴最大振动只有76 μm。

在现场开展了低压转子动平衡试验，表2和表3分别给出了低压Ⅱ转子和低压Ⅰ转子动平衡试验数据。为了能够与瓦振影响系数相比，表中所给出的垂直方向绝对轴振和相对轴振影响系数已经过坐标变换，转换到垂直方向。

由加重前后振动数据可以计算出影响系数：

(14)

影响系数反映了在转子两端分别加1 kg∠0°和1 kg∠180°配重后的振动响应。

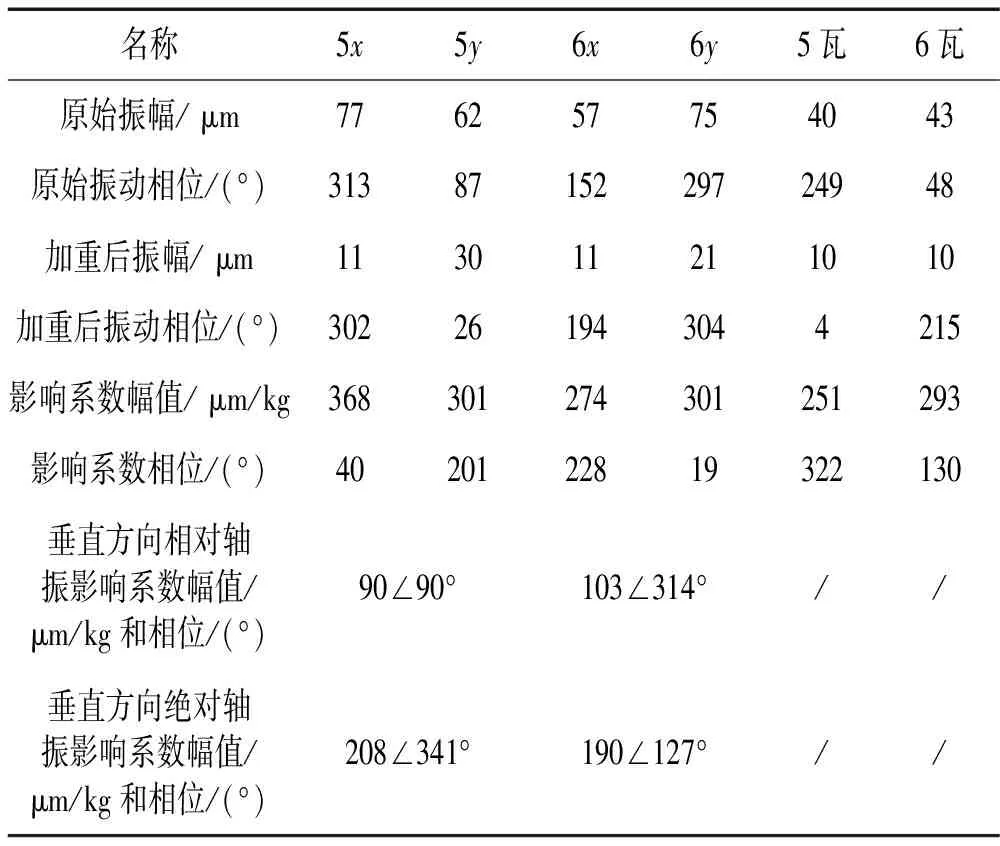
表2 低压转子Ⅱ动平衡数据

在低压Ⅱ转子两侧加反对称平衡配重后，相对轴振影响系数幅值较小，相位和瓦振影响系数相位相差130°～180°，绝对轴振影响系数和瓦振影响系数幅值相近、相位相近，分析表明低压Ⅱ转子两侧座缸式轴承的支撑刚度较弱。

表3给出了低压Ⅰ转子加重前后振动数据。在低压转子Ⅰ两侧加反对称平衡配重后，垂直方向上相对轴振影响系数相位和瓦振影响系数相位相近，瓦振影响系数幅值较小，垂直方向绝对轴振和相对轴振影响系数幅值相近，说明低压Ⅰ转子两侧座缸式轴承的支撑刚度较强。

表3 低压Ⅰ转子动平衡数据

该型汽轮机两个低压缸结构相同，振动现象不完全相同。很多人认为振动大是由于低压缸共振引起的。同一台机组结构相同的两个汽缸的共振特性不可能有如此大的差别。分析表明，不同安装状态下低压缸裙部与基础台板之间的接触状况不同，座缸式轴承的支撑刚度不同，因而振动特性不同。

5 结 论

(1) 大型汽轮机低压转子两侧座缸式轴承振动分析必须考虑支撑刚度影响，本文所提出的等效模型简单方便。

(2) 支撑刚度会同时影响系统等效刚度和等效阻尼。不同支撑刚度下系统振动特性不同。弹性支撑下，轴振和瓦振之间相位差可能较大。支撑特性可以根据绝对轴振、相对轴振和瓦振幅值和相位之间的关系进行分析。

(3) 座缸式轴承监测绝对轴振比监测相对轴振更有意义。座缸式轴承振动受不平衡力的影响较大，可以通过精细动平衡降低振动。

[1] 张学延,史建良,李德勇. 国产600MW汽轮发电机组振动问题分析及治理[J]. 热力发电，2009，38(9)：1-6.

ZHANG Xue-yan, SHI Jian-liang, LI De-yong. Analysis and treatment of vibration for 600MW turbogenerator unit made in China[J]. Thermal Power，2009,38(9)：1-6.

[2] 郭玉杰,张文涛,刘占辉,等.真空变化对大型汽轮发电机组轴承标高和振动的影响分析[J].电站系统工程，2012,28(3)：50-52.

GUO Yu-jie, ZHANG Wen-tao, LIU Zhang-hui, et al. Influence analysis of cylinder vacuum on bearing elevation and vibration[J]. Power System Engineering，2012,28(3)：50-52.

[3] 石可重,李延波,武新华,等. 排汽缸刚度有限元分析[J].汽轮机技术，2001,43(6)：344-346.

SHI Ke-zhong, LI Yan-bo, WU Xin-hua, et al. The rigidity analysis of LP cylinder with limited element calculation[J]. Turbine Technology，2001,43(6)：344-346.

[4] 杜连秀,张伟忠. 汽轮机低压缸刚性有限元分析[J].汽轮机技术，2005,47(6)：428-429.

DU Lian-xiu, ZHANG Wei-zhong. Analysis of turbine LP with FEA[J]. Turbine Technology，2005,47(6)：428-429.

[5] 单世超,陈伯树,平路光. 大型汽轮机轴承支撑刚度研究[J]. 汽轮机技术，2012,54(3)：201-203.

SHAN Shi-chao, CHEN Bo-shu, PING Lu-guang. Research of stiffness of the bearing support for large steam turbine[J]. Turbine Technology，2012,54(3)：201-203.

[6] 孙庆,李汪繁,王秀瑾. 600MW超临界空冷机组基础及轴承座刚度研究[J]. 发电设备，2012,26(4)：217-221.

SUN Qing, LI Wang-fan, WANG Xiu-jin. Research on stiffness of foundation and bearing pedestal for 600MW supercritical air-cooling unit[J]. Power Equipment，2012,26(4)：217-221.

[7] 张宇,陈宇恕,毕勤胜. 转子-轴承-基础非线性动力学研究[J].振动工程学报，1998,11(1)：24-30.

ZHANG Yu, CHEN Yu-shu, BI Qin-sheng. Nonlinear dynamic analysis of rotor-bearing-foundation system[J]. Journal of Vibration Engineering，1998,11(1)：24-30.

[8] Cavala K L, Cavalcante P F, Okabe E P. An investigation on the influence of the supporting structure on the dynamics of the rotor system[J]. Mechanical Systems and Signal Processing,2005,(19):157-174.

[9] Paolo P, Nicolo B, Andrea V. Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: part I-theoretical remarks[J]. Mechanical Systems and Signal Processing, 2006,(20): 662-681.

[10] Chen Yeong-shu, Cheng Ye-dar, Yang Ta-chung, et al. Accurate identification of the frequency response functions for the rotor-bearing-foundation system using the modified pseudo mode shape method[J]. Journal of Sound and Vibration,2010,329:644-658.

[11] Bonello P, Brennan M J. Modeling the dynamic behavior of a supercritical rotor on a flexible foundation using the mechanical impedance technique[J]. Journal of Sound and Vibration,2001,239(3):445-466.

[12] 钟一谔,河衍宗，王正，等.转子动力学[M].北京：清华大学出版社，1987.