超声辐射杆振幅分布与空蚀区域

张 敏，李晓谦，蒋日鹏，郭程熙

(中南大学 机电工程学院，现代复杂装备设计与极端制造国家重点实验室，长沙 410083)

在超声铸造中，超声在金属熔体中产生的空化效应被认为是促进成核及晶粒细化的主要原因。超声空化是指，在强超声场中，熔体中的微小气泡核在声波稀疏相和压缩相的交替作用下，所经历的膨胀、压缩、振荡继而最终崩溃的过程。崩溃瞬间内在极有限的体积内产生高强度的冲击波，促使铝合金熔体中的初生晶被打碎，异质结晶核数目增多，结晶核与固相间的润湿角被减小，从而使凝固组织得到明显的细化[1-6]。在金属熔体中，由于高温、内部不可视及高强度的化学变化，到目前尚无定量测量空化强度和空化范围的有效方法。国内外现有研究中大多通过水及水溶液中的空化试验来研究空化效应[7-10]，或者通过观察超声处理后合金凝固组织特征来研究超声空化的作用[2-5]。对高温熔体中超声空化现象及其对振动系统辐射杆腐蚀规律鲜有研究。

本文通过观测超声振动辐射杆在铝熔体中空化腐蚀特征探究超声波在7050铝合金熔体中产生空化效应所需最小振动幅值，并对铝熔体超声空化阈值作出推测。

1 测试与试验

1.1 试验装置及材料

试验材料为7050铝合金，取自工业铸锭，试验使用设备包括：超声波发生器(超声波电源)；超声振动系统(包含PZT压电陶瓷片，变幅杆，辐射杆)，辐射杆为50×112 mm圆柱体，材料为钛合金。其它辅助装置：电阻炉及配套的温度控制记录仪、热电偶、石墨坩埚(200 mm×165 mm×205 mm)、试验装置如图1所示。

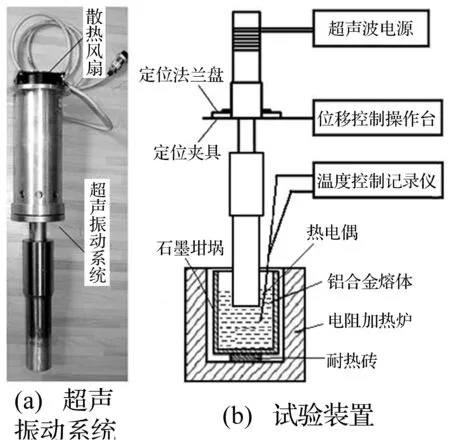
图1 空化腐蚀试验装置示意图

1.2 辐射杆振幅测量

超声振动由压电陶瓷端产生，经阶梯形变幅杆将振幅放大后传递至辐射杆，再将超声能量传输至铝熔体。超声振动的振动幅度一般在微米级别，因此采用高精度的基恩士激光测距仪来测量辐射杆振幅。实验设备如图2所示。在辐射杆端面沿直径方向均布13个测量点，中心测量点在圆心处，测量点之间间隔为4 mm。在柱面沿长度方向布置22个测量点，测量点之间间隔为5 mm，第一个点距离端面1 mm(图2)。测量时将超声振动系统调节至谐振状态，待振动稳定后将频率锁定在谐振点，移动激光探头依次对端面及柱面各测量点进行振幅数据采集，采样频率为392 kHz；采样点数为131 072，每个测量点测量三次。为了尽可能减少测量过程中外界干扰的影响，所有测试工作在隔振台上完成。

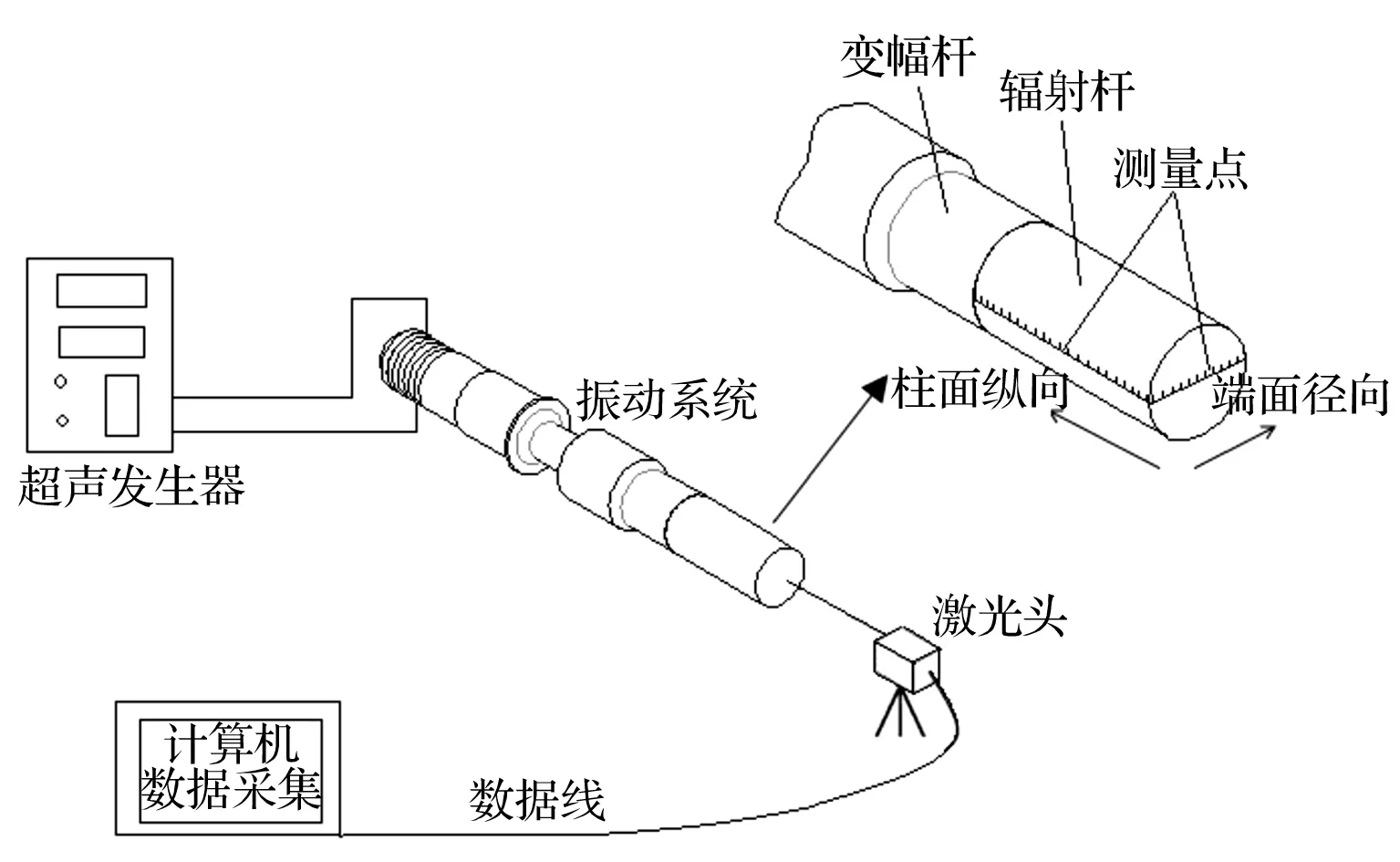
图2 振幅测量装置布局图

1.3 铝熔体中辐射杆空化腐蚀试验

将装有7050铝合金的石墨坩埚置于电阻炉中进行熔炼，待铝块完全熔化后，持续加热至700 ℃，将电阻炉内温度保持700 ℃恒温并对熔体进行超声处理。在辐射杆伸入熔体前，为了防止辐射杆浸入高温熔体时熔体粘附在辐射杆上引起系统失谐，先将辐射杆进行预热[11]。超声波由顶部导入，辐射杆由上部浸入熔体液面70 mm。开启超声发生器并调节至谐振状态。超声振动持续时间为30 h，振动停止后将振动系统从铝熔体中取出，待其冷却后用腐蚀液清除粘附在辐射杆上的铝，观测辐射杆端面和柱面空化腐蚀孔的分布规律。

2 结果与讨论

2.1 超声辐射杆振幅分布规律

经激光测距仪采集到的超声振动信号为离散时间信号，将振动信号进行加矩形窗的快速傅里叶变换(FFT)后，进行频谱分析。以端面圆心处为例，该点振动位移信号与幅频特性如图3所示。分析该点幅值谱得到该点振动频率为20 220 Hz，振动幅为12.718 6 μm。

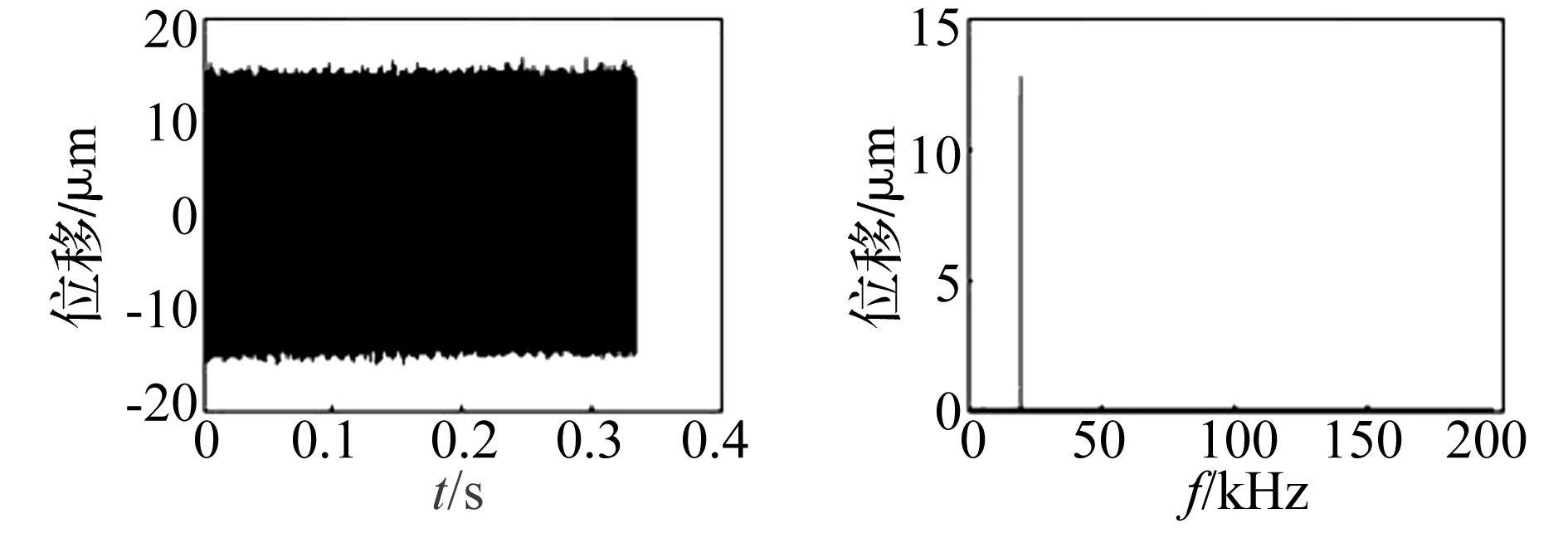
图3 端面圆心处振动信号及幅值谱

由于FFT 频谱分析方法在对离散信号进行频谱分析时，离散信号进行了时域截断，不可避免的产生了能量泄漏，使得谱峰值变小，精度降低。现有的研究表明，使用加窗的比值校正法可达到非常高的精度，可使得频率误差小于0.000 1Δf，幅值误差小于万分之一[12]。本文采用比值校正法对测量点振动信号的幅值谱进行校正，采用校正后的幅值作为该点振动的位移幅值。以端面圆心处为例，运用MATLAB编写频谱校正程序对该点幅值谱进行校正[13]，经校正后该点的振动频率为20 216 Hz，振幅为13.499 μm。其他测量点均按照上述方法得到其振幅值。进而得到端面纵向振动与柱面横向振动幅值分布，如图4所示。

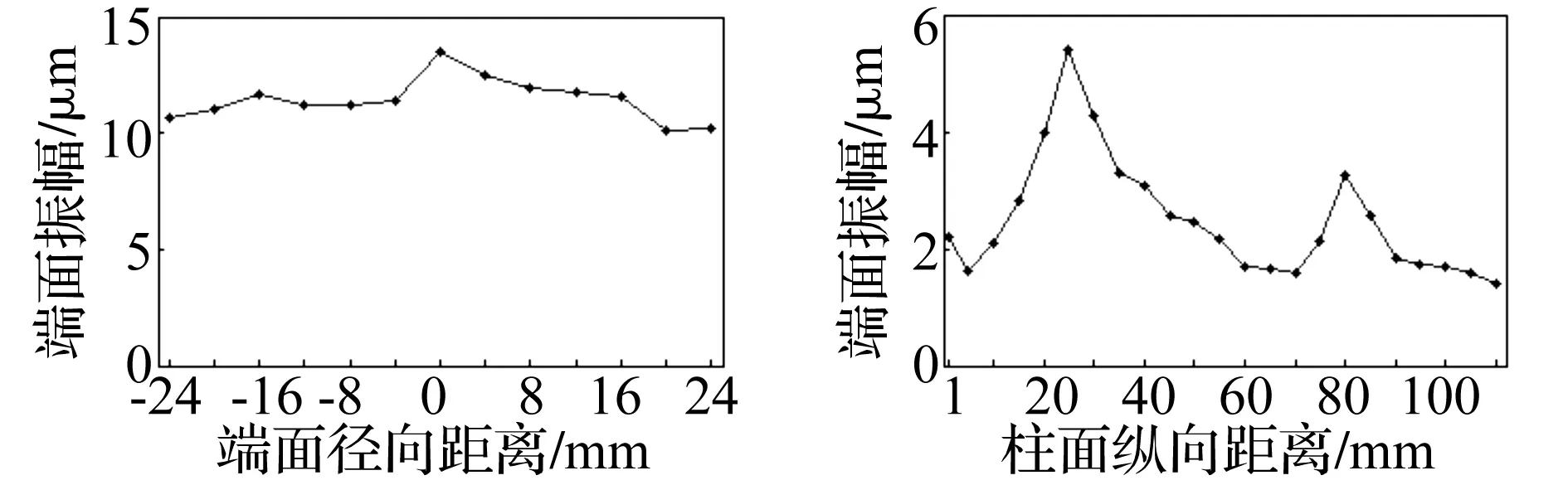
图4 辐射杆端面与柱面振幅分布

由图可知,纵向振动幅值明显大于径向振动幅值，即系统振动以纵向振动为主。辐射杆端面上各测量点振动幅值均在10 μm以上，且幅值分布较为一致，这有利于在超声铸造过程中将超声能量均匀导入铝熔体中。而辐射杆柱面径向振动位移幅值沿长度方向上分布不均，存在两个振幅峰值点，径向振动振幅最大值为5.076 μm，达到纵向振动幅值的1/2，这表明该辐射杆存在较强的纵横耦合振动。由超声振动系统设计理论可知，当振动体横向尺寸大于1/4波长时，其横向振动不能忽略[14]。该辐射杆直径为50 mm，钛合金中超声波波长为205 mm，辐射杆直径接近1/4波长，此时振动体振动为纵横耦合振动。

2.2 辐射杆空化腐蚀特征

经过空化腐蚀试验后，超声振动系统辐射杆的质量损失为85.3 g,辐射杆空蚀前后对比见图5。

图5 辐射杆空化腐蚀前后对比

由图可知，经空化腐蚀试验后，辐射杆端面与柱面均出现了空化腐蚀形成的凹坑，其中端面上的空化腐蚀孔均匀分布在整个辐射面上。圆柱面上各区域则呈现出不同腐蚀程度特征，靠近端面的Ⅰ区和远离端面的Ⅲ区，没有出现空化腐蚀孔。而在Ⅱ则集中分布了大量空化腐蚀孔(见图5(b))。其中，I区距离端面12 mm, Ⅲ区距熔体液面为15 mm，两者对于腐蚀区域Ⅱ区呈对称分布。

已有研究表明：空化腐蚀孔是由熔体中空化气泡溃灭时所产生的微射流对近壁面的冲击所形成[15-17]。在熔体中，空化气泡在声波负压相作用下形成并长大，在相继而来的声波正压相中，气泡又被突然压缩直到崩溃，在空化泡爆破的瞬间形成微射流。气泡离壁面距离不同，其溃灭产生的微射流到达壁面的强度也不同。并不是每一个气泡溃灭都可以给壁面造成空蚀破坏，只有那些靠近壁面的空化气泡溃灭，其微射流冲击才能破坏壁面[17]。对比辐射杆腐蚀形貌(图5)与位移分布图(图4)可知，辐射杆端面振幅较大且分布均匀，端面附近的铝熔体产生空化并对端面形成明显的空化腐蚀。而辐射杆柱面径向振动振幅分布不均，圆柱面附近铝熔体中空化主要发生在Ⅱ区，Ⅰ区与Ⅲ区表面附近的铝熔体并未产生空化，使得Ⅱ呈现明显的空化腐蚀特征，Ⅰ区与Ⅲ则没有出现空化腐蚀。采用差值法计算得到Ⅰ区与Ⅱ区分界处振幅为2.09 μm,Ⅱ区与Ⅲ区分界处振幅为2.18 μm。由此认为，当超声波经辐射杆导入铝熔体时，要使铝熔体产生空化并对近壁面造成空化腐蚀所需的最小振幅约为2.2 μm。

2.3 铝熔体中的声空化阈值

在铝熔体中，只有当足够强的超声传输至熔体时才能产生空化。使铝熔体产生空化所需的最低声压，称为铝熔体的声空化阈值。由于测量超声波在高温熔体中的压强十分困难，因此一般可通过在常规环境下测量其振动特征值，进而转换成在熔体中的工作值。

在声场中，声压幅值与位移振幅有如下关系：

P=2πf·ρc·A

(1)

式中:f为声波频率，ρc为介质的声阻抗，A为位移振幅。

当超声波从钛合金辐射杆透射入另一传播介质时，入射声波与透射声波的声压幅值满足透射公式：

P1=P0·t

(2)

其中:P0、P1分别为入射声波以及透射声波的声压幅值，t为透射系数。透射系数由下式得出：

t=2ρ0c0/(ρ0c0+ρ1c1)

(3)

ρ0c0、ρ1c1分别为传播媒质和辐射杆的声阻抗，各物性参数如表1所示。

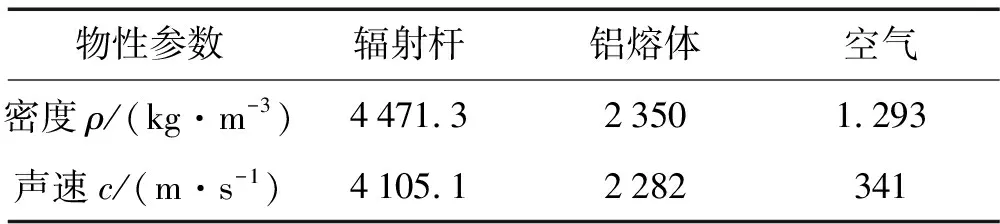
表1 介质物性参数

当超声振动系统在空气中施振时，超声波从辐射杆透射入空气中，由空气中测得的位移振幅值可以得到在辐射杆端面与柱面的透射声压幅值，将透射声压幅值，辐射杆以及空气的声阻抗值代入透射式(2)、式(3)，可得辐射杆中的入射声压幅值，

当辐射杆浸入铝熔体时，超声波透射入铝熔体，将辐射杆中的入射声压幅值，辐射杆以及熔体的声阻抗值代入式(2)、式(3)，得到在铝合金熔体中的辐射杆端面与柱面透射声压幅值。

当辐射杆浸入到铝熔体时，由于熔体负载的作用会引起从压电陶瓷到辐射杆传递途中的功率损耗，在计算声压幅值时需考虑该损耗，由文献[18]知，此功率损耗约占总功率的6.5%，最终得到辐射杆浸入铝熔体70 mm时辐射面各点处透射声压幅值分布，如图6所示。

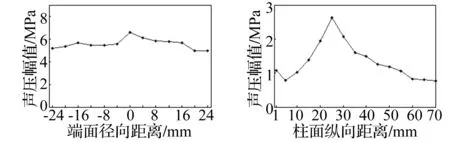
图6 辐射杆端面与周面声压幅值分布

由于辐射面上各点声压幅值与振动位移幅值成线性关系，因此，声压幅值分布趋势与位移振幅分布一致，辐射杆端面声压幅值大于圆柱面声压幅值。根据辐射杆柱面空化腐蚀分界线出现的位置，利用插值法得到柱面Ⅰ区与Ⅱ区、Ⅱ区与Ⅲ区分界处透射声压幅值分别为1.01 MPa和1.09 MPa。由此可估计，在本试验条件下，7050铝合金熔体在700 ℃时空化阈值约为1.1 Mpa，这与Eskin关于铝合金熔体空化阈值研究结果一致[19]。

3 结 论

(1) 铸造用超声系统振动以纵向振动为主，同时存在较强的纵横耦合振动。辐射杆端面振幅分布一致，柱面振幅分布不均并出现两个振幅峰值。

(2) 铝熔体产生空化对超声振动系统辐射杆造成空化腐蚀，辐射杆端面空化腐蚀程度为均匀分布，在辐射杆柱面则只有位移振幅大于2.2 μm的区域才发生空化腐蚀。

(3) 7050铝合金熔体在700 ℃时空化阈值约为1.1 MPa。

[1] 冯若．超声手册[M]．南京：南京大学出版社，1999.

[2] Eskin G I. Broad prospects for commercial application of the ultrasonic (cavitation) melt treatment of light alloys[J]. Ultrasonics Sonochemistry, 2001, 8(3): 319-325.

[3] Li Y L, Feng H K, Cao F R, et al. Effect of high density ultrasonic on the microstructure and refining property of Al 5Ti 0.25 C grain refiner alloy[J]. Materials Science and Engineering: A, 2008, 487(1): 518-523.

[4] Liu X, Osawa Y, Takamori S, et al. Microstructure and mechanical properties of AZ91 alloy produced with ultrasonic vibration[J]. Materials Science and Engineering: A, 2008, 487(1): 120-123.

[5] Komarov S V, Kuwabara M, Abramov O V. High power ultrasonics in pyrometallurgy: Current status and recent development[J]. ISIJ International, 2005, 45(12): 1765-1782.

[6] 马立群, 舒光冀, 陈锋. 金属熔体在超声场中凝固的研究[J].材料科学与工程, 1995, 13(4): 2-7.

MA Li-qun, SHU Guang-ji, CHEN Feng. Research on solidification of metal melt under ultrasonic field[J]. Materials Science & Engineering, 1995, 13(4): 2-7.

[7] Neville A, McDougall B A B. Erosion-and cavitation-corrosion of titanium and its alloys[J]. Wear, 2001, 250(1): 726-735.

[8] 沈再阳，何永勇.基于共振峰的超声空化声发射信号分析[J].振动与冲击,2012,31(16):43-47.

SHEN Zai-yang, HE Yong-yong. Formant method applied to analyze acoustic emission signals from ultrasonic cavitation[J]. Journal of Vibration and Shock,2012,31(16)：43-47.

[9] Wang Y C, Yao M C. Realization of cavitation fields based on the acoustic resonance modes in an immersion-type sonochemical reactor[J]. Ultrasonics sonochemistry, 2012,20:565-570.

[10] Park J C, Han M S, Kim S J. Investigation on the cavitation damage behavior with temperature and cavitation time in seawater[J]. Surface and Interface Analysis, 2012, 44(11-12): 1407-1410.

[11] 黄运明.超声铸造中换能系统失谐现象分析及其设计研究[D]. 长沙：中南大学，2007，1：34-37.

[12] 徐传燕, 丁康, 林慧斌, 等. 离散频谱分析比值校正法幅值和相位的抗噪性分析[J]. 振动工程学报, 2011, 24(6): 633-638.

XU Chuan-yan, DING Kang, LIN Hui-bin, et al. Noise influence on amplitude and phase estimation accuracy by interpolation method for discrete spectrum[J]. Journal of Vibration Engineering, 2011, 24(6): 633-638.

[13] 谢明,丁康. 离散频谱分析的一种新校正方法[J].重庆大学学报, 1995,18( 2) : 47-54.

XIE Ming, DING Kang. A new rectifying technique of discrete spectrum analysis[J]. Journal of Chongqing University,1995,18(2): 47-54.

[14] 周光平,梁明军,王家宣.大尺寸超声振动体的研究[J].声学技术,2004,23(3):183-192.

ZHOU Guang-ping, LIANG Ming-jun, WANG Jia-xuan. Study on large sized ultrasonic vibrators[J]. Technical Acoustics, 2004,23(3):183-192.

[15] 黄继汤. 空化与空蚀的原理及应用[M]. 北京：清华大学出版社，1991.

[16] 薛伟，陈昭运. 空蚀破坏的微观过程研究[J].机械工程材料，2005,29(2):59-62.

XUE Wei, CHEN Zhao-yun. The micro-cours of the cavitation erosion[J]. Materials for Mechanical Engineering，2005,29(2):59-62.

[17] 李永健. 空蚀发生过程中表面形貌作用机理研究[D]. 北京: 清华大学, 2008.

[18] 刘荣光. 超声波在铝熔体中的声场分布和空化效应及其对凝固过程影响[D]. 长沙：中南大学，2007，12：43-44.

[19] Eskin G I. Ultrasonic treatment of light alloy melts[M]. CRC Press, 1998:41-51.