迎风墙面多开孔结构风致内压的试验研究

徐海巍，余世策，楼文娟

(浙江大学 建筑工程学院，杭州 310058)

强风过后的灾后调查表明[1],许多建筑尤其是低矮建筑，其围护结构破坏甚至墙体的倒塌往往是由于较大的内压与外压共同作用而造成。因而开孔结构的风致内压效应也引起了人们的高度重视。关于墙面单一开孔工况下建筑内压作用国内外已经有许多文献[2-7]进行了探讨，并且还一直在进行中。这些研究表明迎风墙面单一开孔结构的内压可以用二阶非线性的常微分方程来进行描述，并且在适当的开孔条件下，内压会产生剧烈共振效应使得其脉动能量得到放大，而该共振响应的大小与开孔面积和结构的内部容积以及外部风场等条件紧密相关。然而由于建筑使用功能和艺术造型的需要，同一墙面实际上可能会存在多个开孔，例如厂房的排窗和仓库的大门等。与单一开孔情况不同的是，多开孔工况将是一个多自由度的非线性振动体系。而国内外关于这种情况下内压动力特性的研究十分有限。Oh等[8]提到对同一墙面多开孔的结构内压控制方程可以由单一开孔工况非线性方程扩充得到。Guha等[9]最近从频域和传递函数的角度对内外压传递方程进行了推导，并由风洞试验考察了迎风面居中开设两个相邻开孔在不同开孔面积比时对内压结果的影响。在恶劣的风环境下这些开孔的存在会对内压响应造成怎么样的影响，与单一开孔相比，多开孔时内压动力特性又会有哪些变化，这些都将是本文研究的重点。本文从时域角度出发结合矩阵特征值的方法对多开孔情况下内压共振频率进行了推导，并由方程线性化得到了系统等效阻尼比的预测公式，通过不同内部容积下迎风墙面单、双开孔模型的风洞试验探索了内部容积变化所造成的影响，同时分析了双开孔情况下内压动力响应与单开孔的区别。

1 迎风面多开孔内压预测理论

1.1 多开孔内压传递方程推导

基于非定常的伯努利方程，单一开孔的风致内压响应可以表达为单自由度的非线性的振动模型[10]:

(1)

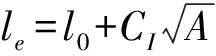
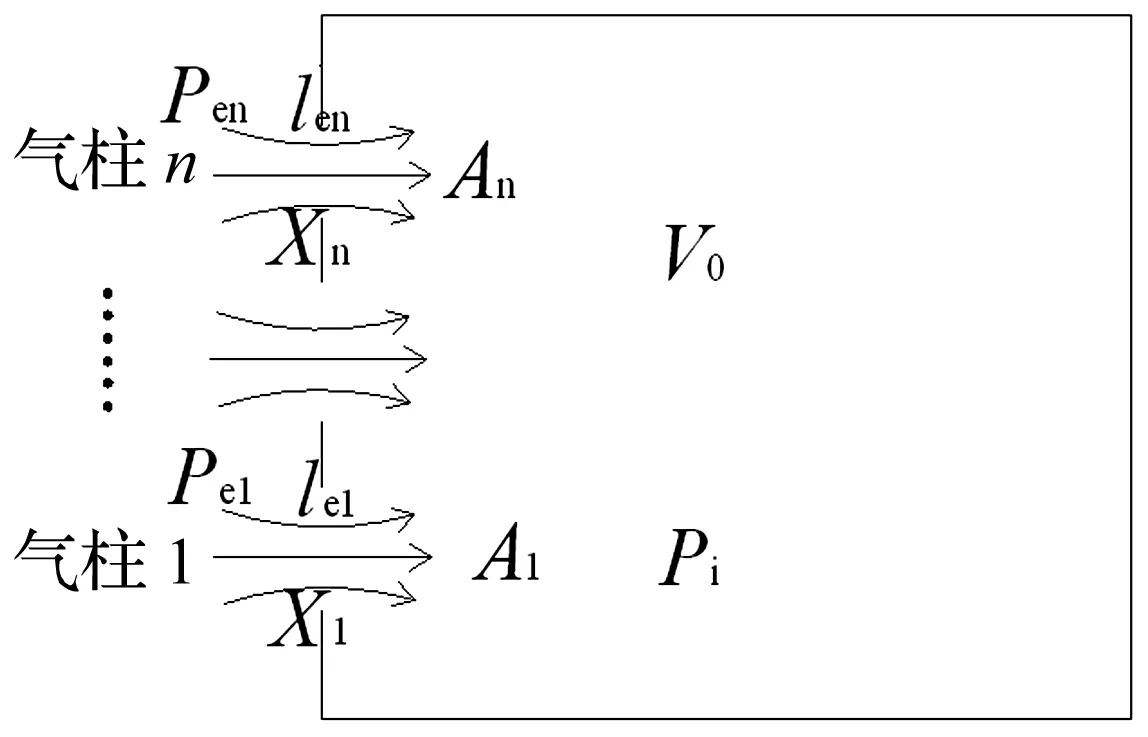
图1 迎风面多开孔计算模型

当迎风面存在多个开孔时，其计算模型如图1所示。对每个开孔分别应用公式(1)可以得到任意个开孔情况下内压响应方程:

(2)

引入连续性假定和等熵绝热方程得到：

(3)

式中γ和P0分别为开孔周围空气的比热比和压强；An为第n个开孔的面积，V0为结构内部容积；将方程(3)代入式(2)中并表示为矩阵形式得到：

(4)

其中质量矩阵:

[M]=diag[ρaLe1,ρaLe2,…,ρaLen]

非线性的阻尼矩阵为:

刚度矩阵

忽略方程(4)中的阻尼项和外力项，并求解矩阵特征根得到同一墙面任意多开孔情况下内压的Helmholtz共振频率为：

(5)

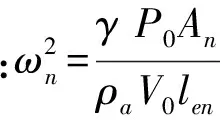
1.2 方程线性化及等效阻尼比

为了研究孔口气柱振荡的阻尼特性，对方程(2)进行线性化。假定内压为正态分布的前提下，采用概率平均线性化方法[10]可得：

(6)

故方程(4)变为：

(7)

其中等效阻尼系数：

对于经典阻尼体系其等效阻尼比可以表示为：

(8)

式中:Me=φTMφ，Ce=φTCeqφ，φ为模态。

1.3 双开孔控制方程

最简单的多开孔形式为迎风面双开孔，由式(5)和式(8)可得其相应的内压共振频率和等效阻尼比分别为：

(9)

(10)

为了与单一开孔下内压阻尼进行比较，方程(11)给出了单一开孔时内压等效阻尼比：

(11)

2 风洞试验研究

2.1 试验工况及风场

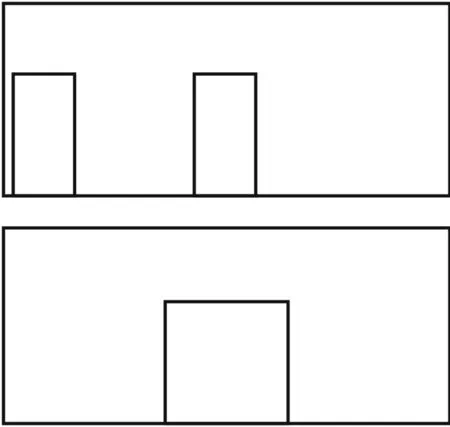
图2 迎风面开孔示意图

为考察上述方法的有效性并研究多开孔和单一开孔对内压脉动响应的影响，分别对迎风面居中开设10 cm×10 cm的单一开孔模型，以及迎风面开设2个5 cm×10 cm的双开孔模型进行了风洞试验，模型尺寸为36.4 cm×54.8 cm×16 cm，采用有机玻璃制成。两种迎风面开孔示意图见图2。与Guha[9]等采用靠近中心的对称开孔方式不同的是本文采用的开孔为偏心形式。另外为了反映内部容积变化的影响，每种开孔分别在在V0，1.5V0，2V0，3V0，4V0，4.5V0(V0为模型的容积)这6种容积下进行试验。模型的不同内部容积是通过转盘底下尺寸为55 cm×36 cm×55 cm的大体积空腔的调节来实现的，模型测点布置如图3所示。

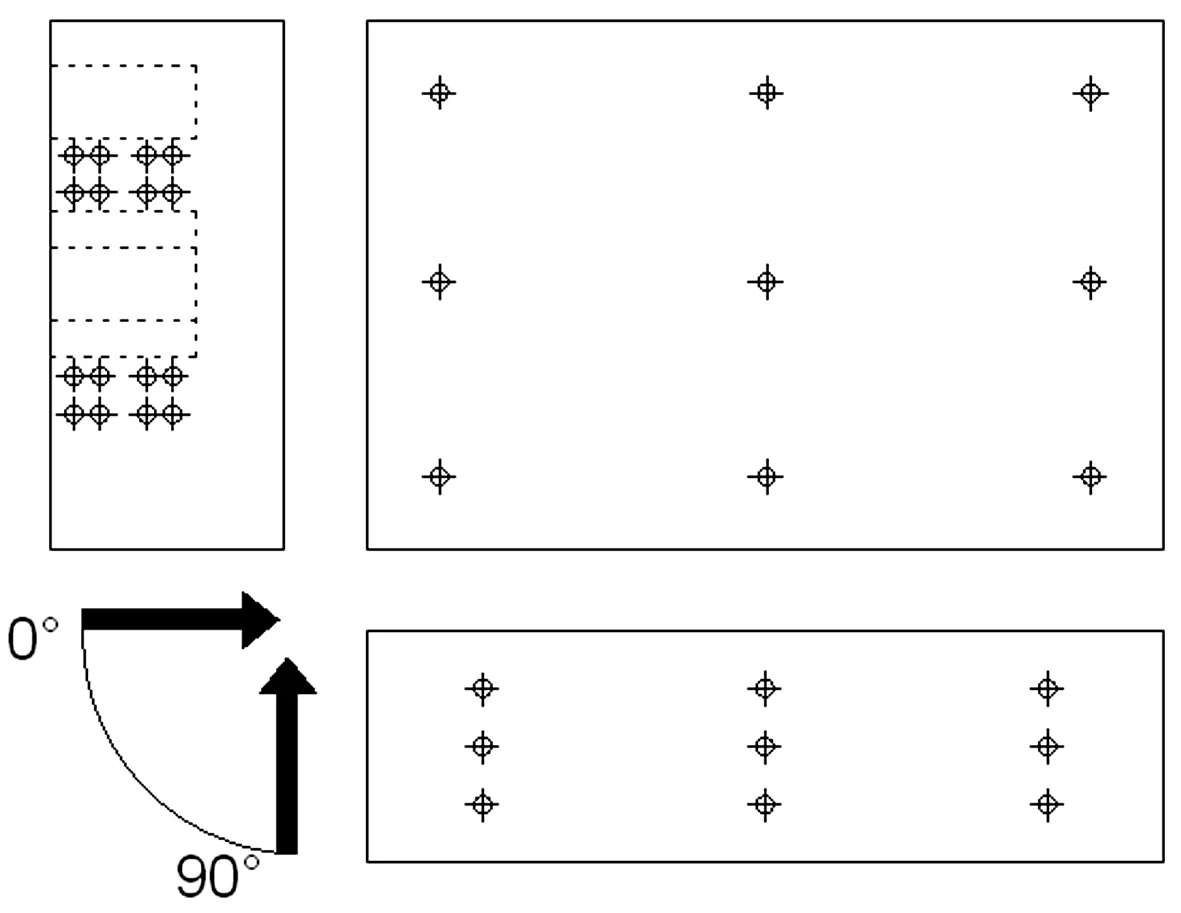
图3 风洞试验模型测点布置

本次试验在浙江大学ZD-1风洞实验室进行，试验风场为1∶250缩尺比下规范B类地貌。风洞中模拟的风剖面和湍流度与规范的比较见图4，对应实尺100 m高度处脉动风速谱与Kaimal谱的比较如图5所示。试验参考点取在模型屋面即16 cm高度处。参考点风速为12.8 m/s。压力时程采用ZOC33扫描阀采集，采样频率为625 Hz，每个通道均采集32 s。试验中对模型开孔迎风面正负90°范围的风向角进行测试，间隔为15°。风向角定义可参见图3。

图4 模拟的平均风速和湍流度剖面与规范比较

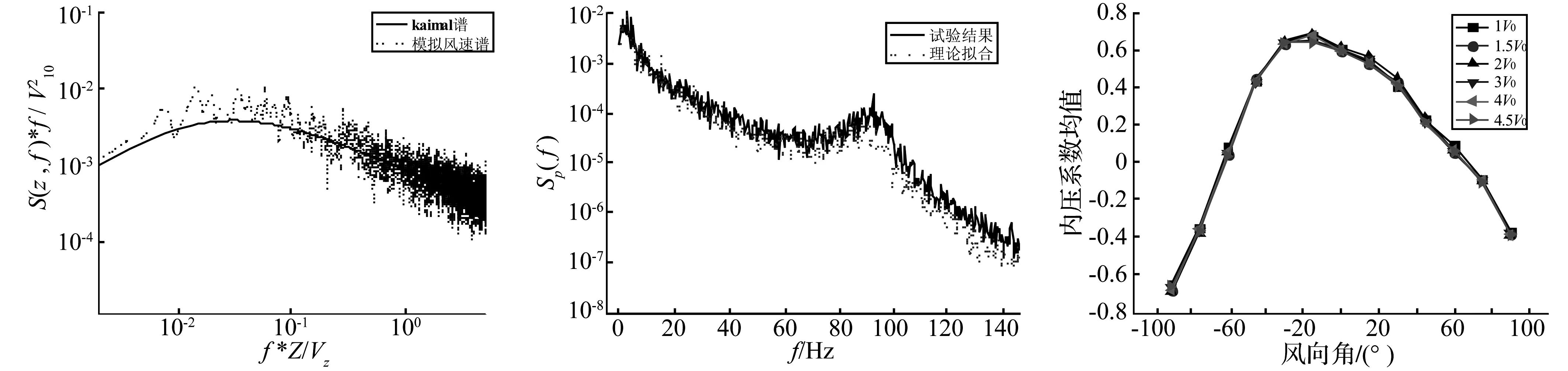
图5 0.4 m高度处脉动风速功率谱密度与Kaimal谱

2.2 控制方程有效性验证

为了验证控制方程组的精度，图6对1V0容积下双开孔模型内压试验功率谱和理论拟合结果进行了对比。理论拟合时的参数取值为：CI1=1.3，CI2=1.7，CL1=CL2=5。图6说明当取适当的参数值后，多开孔方程(2)能够准确描述内压的脉动响应。表1给出的内压共振频率的理论预测值和试验值的比较也说明频率预测方程(5)是合理的。

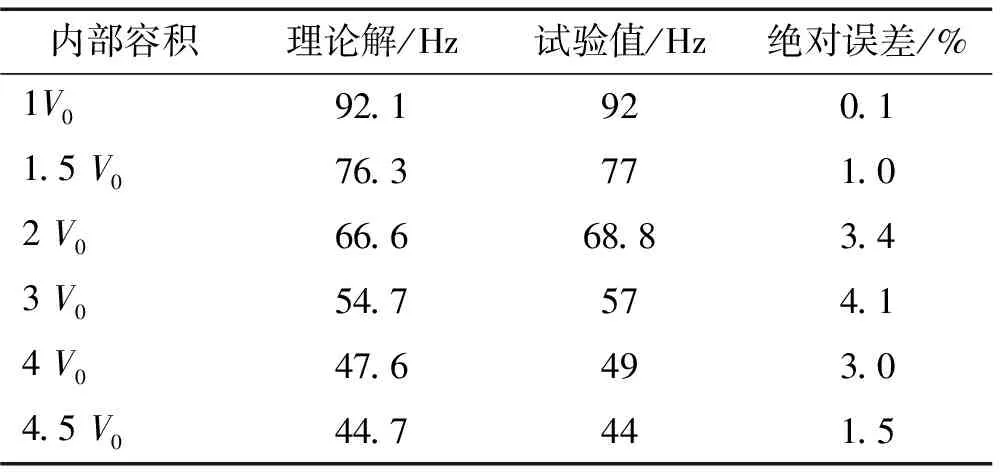
表1 Helmholtz频率理论解与试验值

2.3 内部容积的影响

图7、8分别给出了不同内部容积下，迎风面双开孔模型内压均值均方根随风向角的变化规律，由图7可见容积变化对模型内的压力均值影响不大，最大正压力在-15°风向角附近取得，而最大吸力出现在-90°风向角。这是由于开孔的非对称分布所造成。因为在±90°风向角下，开孔山墙处在侧风向，山墙上风压沿着来流方向递减。但-90°风向角时两个开孔更加靠近来流风向，由文献[9]可知当各开孔面积相同时，平均内压系数等于各开孔处平均外压系数的平均值。故相比90°风向角，-90°风向角时内压吸力更为不利。而图8则表明内压脉动最为剧烈的仍然为-15°风向角，除此之外在-60°时内压脉动均方根也较大。而所有容积中内压脉动响应最强烈的为内部容积为2V0的工况。这可能受外部风荷载激励能量的大小以及气柱振荡阻尼的综合影响而造成。从表1可知，内部容积增加导致内压共振频率降低，因而所对应的外荷载激振能量会增强，在合适阻尼比下就可能会造成强烈的共振效应。

表2给出了不同内部容积模型在0°风向角下内压等效阻尼比值，可以发现随着容积增大系统内部的阻尼逐渐增加。而图9中V0容积下模型阻尼比随风向角的变化则说明在不同风向角下系统的阻尼也不尽相同，在模型开孔垂直于来流范围内即-40°～20°风向角下取得较大值而在此范围之外阻尼比随着来流向与开孔法线方向夹角增大而迅速减弱。这就说明斜风向下的Helmholtz共振效应可能会大于迎风时,这一点可由图10和图11，V0容积下0°和60°风向角下内压的功率谱可以证明。图中外压取的是两个孔口的平均外压。对比这两张图可以发现，60°风向角下内压共振峰明显超过0°时，共振响应也更加剧烈。

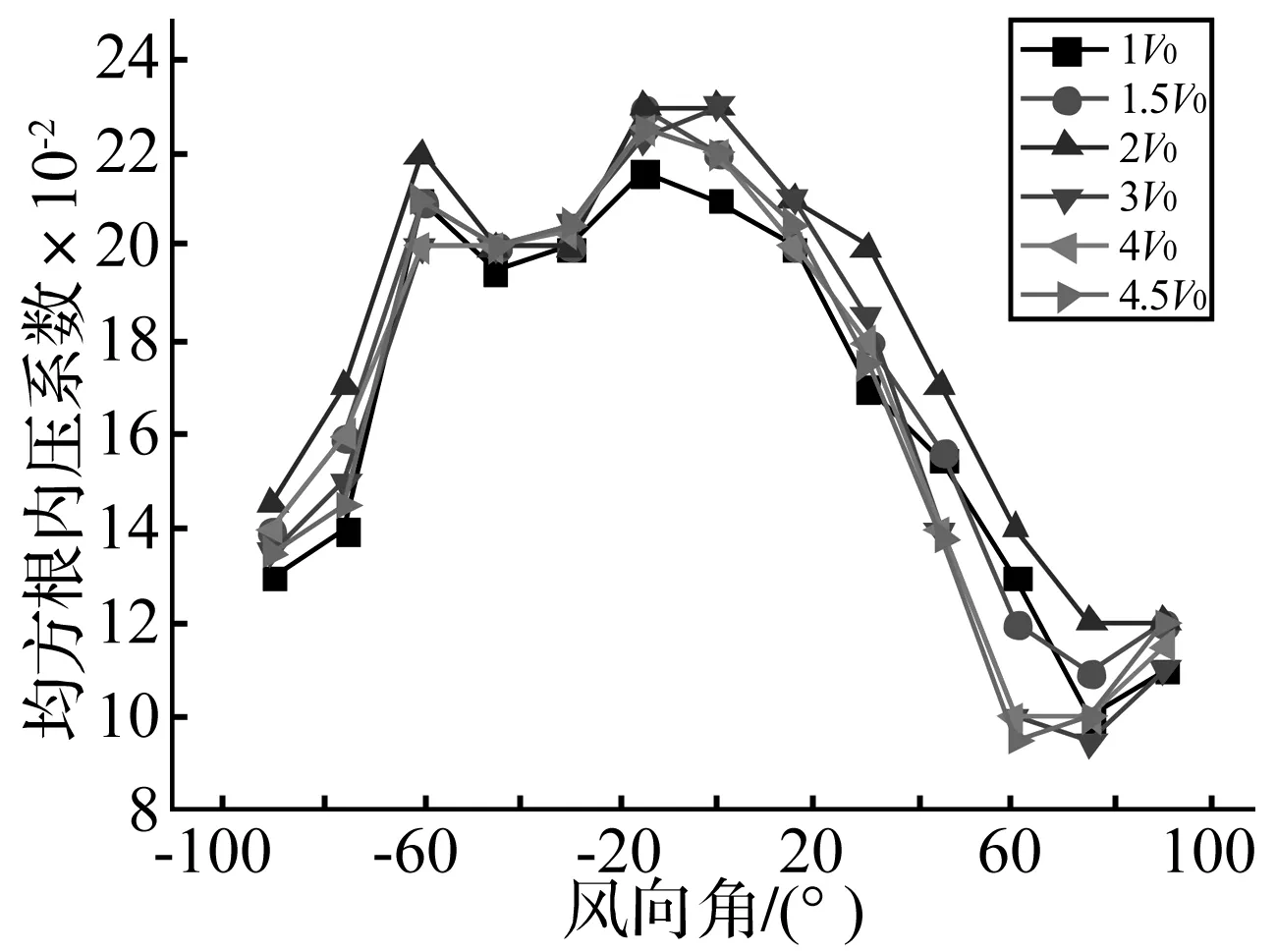
图8 迎风面双开孔模型内压系数均方根值

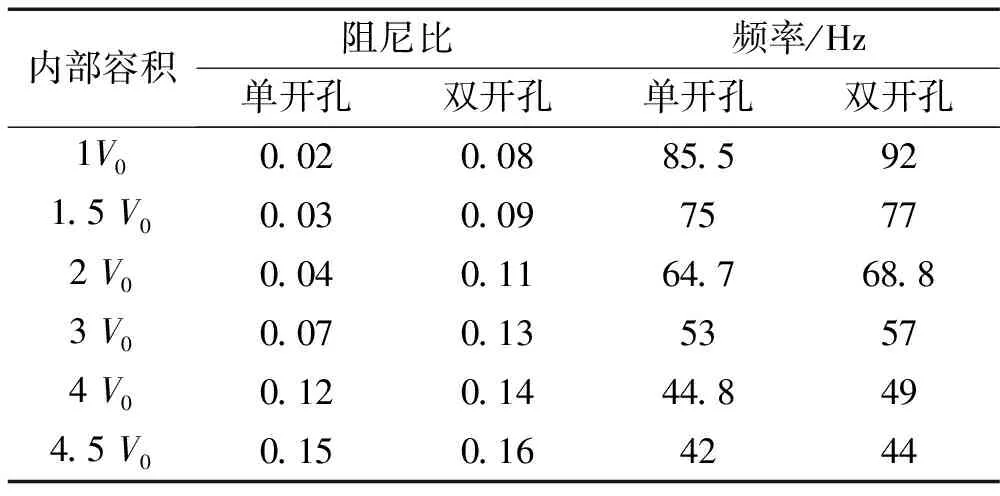
表2 0°风向角下单、双开孔模型共振频率与阻尼比

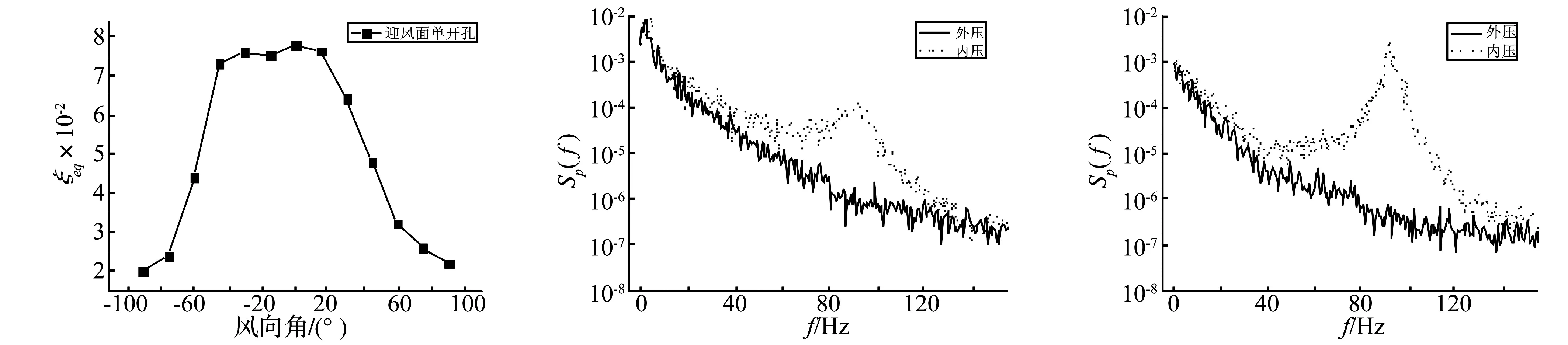
图9 V0容积下迎风面双开孔模型等效阻尼比

3 单、双开孔内压动力特性比较

为了比较迎风面多开孔对内动力特性影响，将开孔面积相同的迎风面单开孔和双开孔模型的共振频率和阻尼比等内压动力特性参数的试验识别结果列于表2中。从表2可知单开孔时内压共振频率普遍小于双开孔的情况。也就说随着开孔数增加内压共振频率所对应的外部激励能量会随之减弱。同样就阻尼比而言，单开孔情况也要小于双开孔。

图12-图13则给出了两种不同开孔方式下内压均值和均方根，图12表明单开孔内压均值在0°～60°范围内更大，而-15°～-45°风向角下小于双开孔。这可能是由于双开孔模型的开孔位置偏心所造成。而双开孔内压的脉动均方根值除了在-45°～-75°时大于单开孔，其余风向角下均小于单一开孔。这可能是由于-45°～-75°这些风向角下两开孔更加靠近来流，外压脉动相对较大。

为更好的评估两种开孔情况下的共振响应效果，图14给出了V0容积模型在不同风向角下内外压脉动均方根之比。其中外压的脉动均方根取的是开孔位置外压脉动的面积加权平均值。从图14可知，在60°以外的其他风向角下，双开孔的内外压脉动均方根之比均小于单开孔的情况，这是因为与双开孔相比，单开孔系统具有更低的阻尼比，且共振频率下拥有更高的激振能量。而在60°风向下双开孔和75°风向时单开孔分别有最大的内外均方根之比表明此时共振效应最为明显，这一点由图10和图11的比较也可以说明，Sharma等[12-13]认为这可能是斜风向下的剪切流效应影响所造成。

图12 单、双开孔模型内压系数平均值

4 结 论

本文由单一开孔模型内外压传递方程的拓展得到了同一墙面多开孔模型的内压响应的控制方程，并通过不同容积下迎风面双开孔模型的和相同面积的单开孔模型进行风洞试验研究了模型内部容积以及多开孔对内压动力特性的影响，主要结论如下：

(1) 对试验结果的拟合表明所推导的多开孔内压控制方程有较好的精度。

(2) 随着内部容积增加多开孔模型风致内压的共振频率降低而阻尼比增加。容积变化对内压均值影响不大，在试验风向角中模型在垂直来流附近风向角中，内压阻尼比较大，而在斜风向下较小，故斜风向下内压共振响应更为剧烈。

(3) 与迎风墙面单一开孔相比，多开孔会导致内压共振频率和阻尼比增加。除个别风向角外，双开孔内外压脉动均方根之比小于单开孔的情况。迎风面单、双开孔最大内外压脉动均方根之比出现在75°和60°斜风向。

[1]孙炳楠. 9417号台风对温州民房破坏的调查[R].杭州：浙江大学,1995.

[2]卢旦, 楼文娟, 唐锦春. 开孔结构风致内压研究[J]. 浙江大学学报:工学版.2005,39(9):1388-1392.

LU Dan, LOU Wen-juan, TANG Jin-chun. Study on wind-induced internal pressure of opening structure[J]. Journal of Zhejiang University :Engineering Science, 2005, 39(9):1388-1392.

[3]余世策, 楼文娟, 孙炳楠,等. 开孔结构内部风效应的风洞试验研究[J]. 建筑结构学报, 2007,28(4):76-82.

YU Shi-ce, LOU Wen-juan, SUN Bing-nan, et al. Wind tunnel study on internal wind effect for structure with openings[J]. Journal of Building Structures, 2007,28(4):76-82.

[4]Holmes JD. Mean and fluctuating pressures induced by wind[C]// Proceedings of 5thinternational conference on wind engineering. Fort conllins, Colorado:[s. n.],1979:435-450.

[5]Liu H, Saathoff P J., Building internal pressure: sudden change[J]. Journal of Engineering Mechanics, 1981,107(2): 309 -321.

[6]Ginger J D,Mehta K C ,Yeatts B B. Internal pressures in a low-rise full-scale building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997,72 :163-174.

[7]Holmes J D, Ginger J D. Internal pressure-the dominant windward opening case-A review[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012,100(1): 70-76.

[8]Oh H J, Kopp G A, Inculet D R. The UWO contribution to the NIST aerodynamic database for wind load on low buildings: Part 3.Internal pressure [J]. Journal of Wind Engineering and Industrial Aerodynamics. 2007,95:755-779.

[9]Guha T K, Sharma R N, Richards P J. Internal pressure in a building with multiple dominant openings in a single wall: Comparison with the single opening situation[J]Journal of Wind Engineering and Industrial Aerodynamics,2012,107&108:244-255.

[10]Vickery B J, Bloxham C. Internal pressure dynamics with a dominant opening [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41 :193-204.

[11]Inculet D R, Davenopt A G. Pressure-equalized rainscreens: A study in the frequency domain [J]. Journal of Wind Engineering and Industrial Aerodynamics,1994,53(1-2):63-87.

[12]Sharma R N, Richards P J. The influence of Helmholtz resonance on internal pressures in a low-rise building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(6):807-828.

[13]Sharma R N, Mason S, Driver P. Scaling methods for wind tunnel modeling of building internal pressures induced through openings[J]. Wind and Structure,2010,13:363-374.