基于稀疏编码的振动信号特征提取算法与实验研究
苗中华,周广兴,刘海宁,刘成良
(1.上海大学 机电工程与自动化学院,上海 200072;2. 上海交通大学 机械与动力工程学院,上海 200240)
重大装备的安全服役与智能维护是我国装备制造业面临的重要课题。相比定期维护及事后维修,基于状态的设备维护(Condition-Based Maintenance, CBM)被认为是目前最有效的维护策略[1]。然而,基于状态的设备维护需要采集多路传感信息,尤其在低转速条件下连续长时间采样,将造成海量冗余数据。如何在海量冗余数据中进行信号有效特征提取是智能维护领域亟需探索的基础理论和关键技术难题。
在铁路系统的常规维护中,工人用铁锤敲击机车车轮,根据敲击声音来判断车轮是否有裂纹;工程领域中经验丰富的维护人员根据机器工作时发出的声音就能够判断机器是否运行正常。上述现象潜在的物理原理是由于零部件损伤改变了其特征频率,进而改变了声音的音色。然而,工程应用领域对这种仅凭听力系统所实现的生物本能诊断能力的运作原理,包括耳朵对声音信号的处理及大脑中诊断知识的建立,却鲜有解释。
Barlow[2]开创性地提出了视神经系统信息处理的一个基本原则是:冗余度压缩(Redundancy Reduction)。进一步地,Földiák[3]将稀疏编码(Sparse Coding)的概念与冗余度压缩建立了联系。基于上述假设性研究,Olshausen等[4-5]首先在《Nature》杂志上发表论文指出:从自然图像中学习出了与哺乳动物初级视觉皮层神经元具有相同特性的基函数,并进一步将稀疏编码解释为诸多生物传感系统信息处理的基本策略。Smith等[6]也在《Nature》上发表论文验证了移不变稀疏编码(Shift-Invariant Sparse Coding)是生物听觉系统的有效建模手段,并提出了相应的基函数学习方法。上述研究表明:移不变稀疏编码可以作为维护人员仅凭听力系统所实现的生物本能诊断能力的一种有效解释,其必然也应具有在机械旋转设备故障诊断中应用的潜力。
本文借鉴神经科学研究的相关进展,在前人探索研究的基础上[7-8],从模拟人耳对声音信号处理原理的角度,研究利用稀疏编码进行信号有效特征提取的若干问题,并进行实验验证。
1 稀疏编码模型及求解
1.1 稀疏编码模型
稀疏编码的概念源于视神经网络的研究,是对只有小部分神经元同时处于活跃状态的多维数据神经网络的表示方法。就生物神经学而言,稀疏编码是指:生物感知系统进化极度高效的编码策略来最大化传递到大脑的信息,同时最小化能量的消耗与对神经资源的占用——感知信息由海量存在的神经元中极少数激活神经元所表示。从数学的角度讲,稀疏编码被假设为是对多维数据进行线性分解的一种表示方法。一个输入信号X=[x1,x2,…,xM]T可以被表示成基函数的加权和,再加上附加噪声:
(1)
式中,矩阵D∈RM×K被称作字典(Dictionary),其中列向量为基函数dk,又称作原子(Atoms),s=[s1,s2,…,sK]T是输入信号x的稀疏表示(Sparse Representation),ε通常假设为高斯噪声。
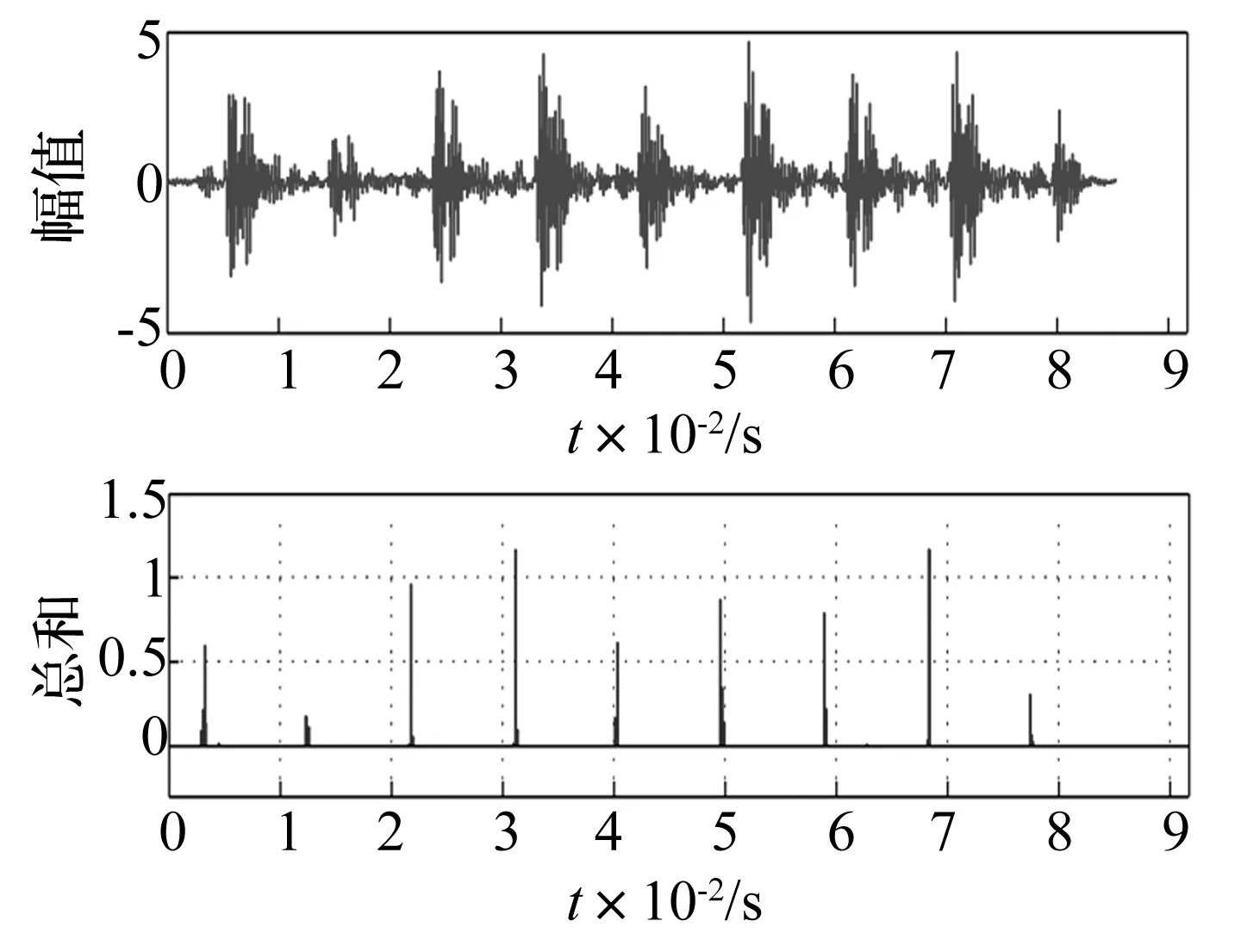
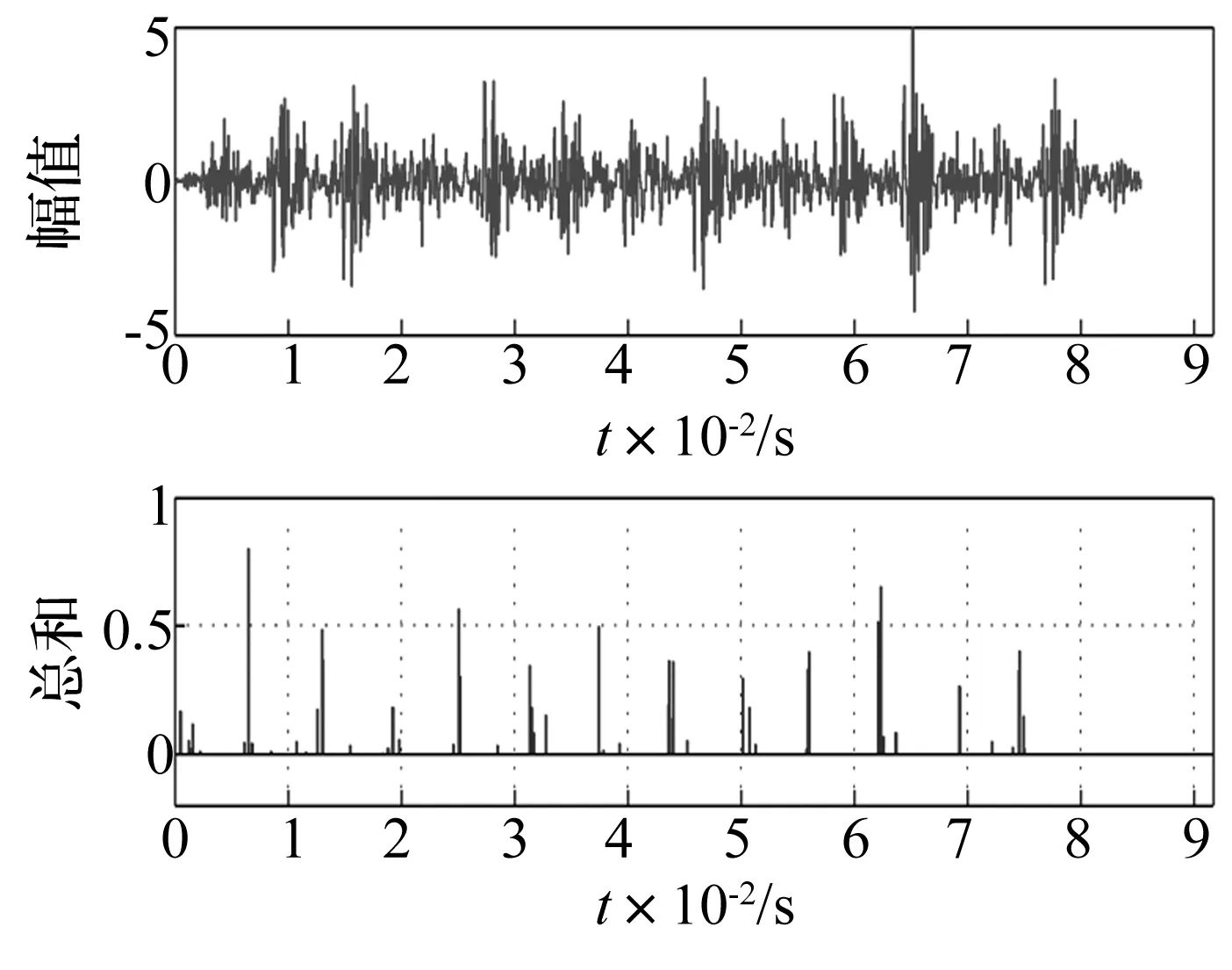
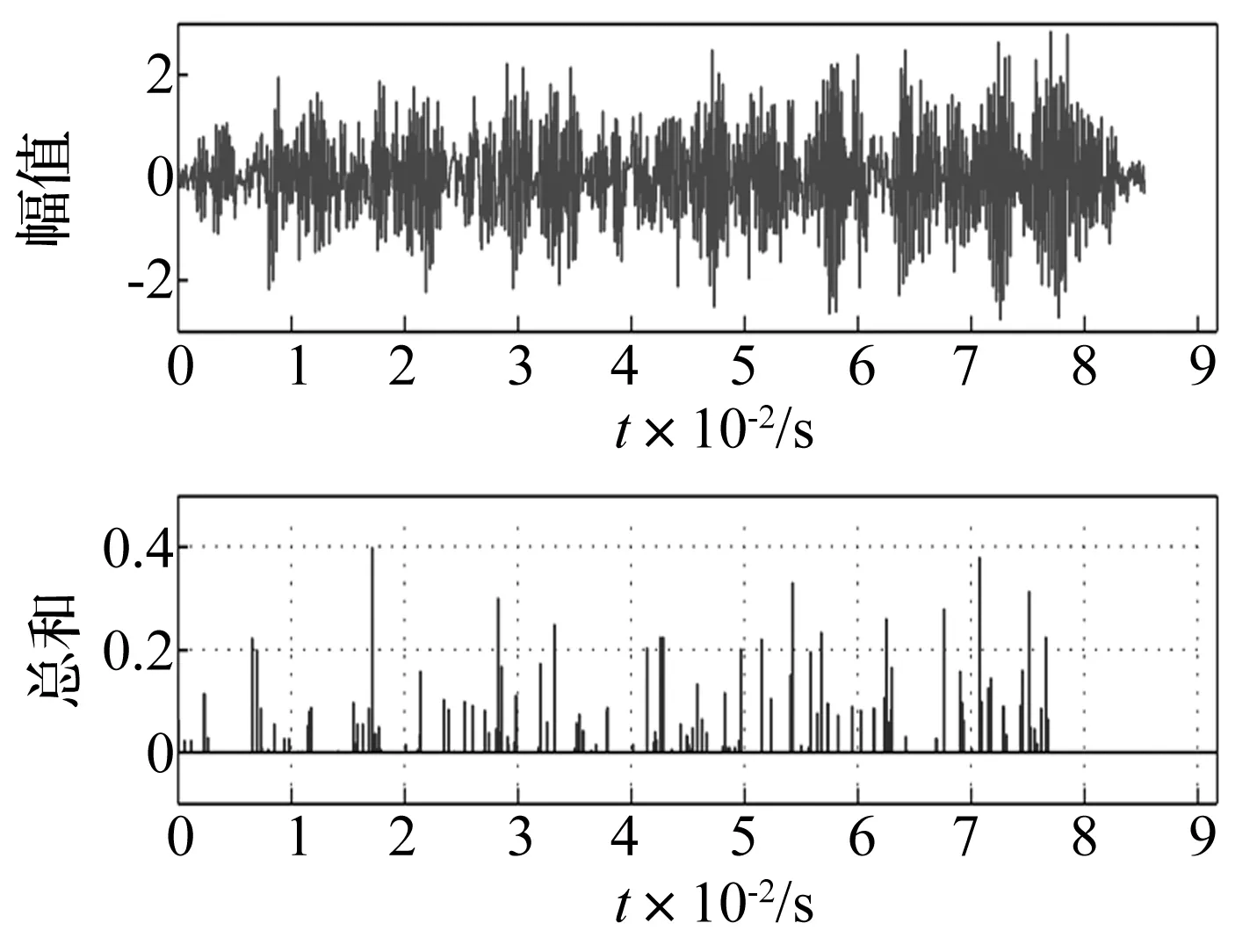
稀疏编码即是基于给定信号x与字典D求解稀疏表示s。在式(1)所示的模型中,基函数的个数可以大于输入信号的维数,即:M (2) 从本质上讲,稀疏性是上述两个问题的共同优化目标。对字典学习而言,稀疏性能够促进基函数对数据特征模式的捕捉;对系数求解来说,稀疏性从模式识别的简约原则(Parsimony Principle)[9]上能够使得后续推理过程变得简单。 基于给定字典精确求解信号的稀疏表示被证明是一个NP-Hard问题[10],通常采用匹配追踪算法[11-12]或者最大后验概率估计(Maximum A Posterior, MAP)[13-14]近似求解。 (3) (4) (5) (6) (7) 同时,每一个样本的似然可以被表示成: (8) 根据式(4)中的似然函数,并假设系数的先验概率分布为Laplace分布,则似然式(8)可被推导为: (9) (10) 式中第一项可以看作逼近误差,第二项可以看作具有惩罚参数β=2σ2θ的稀疏约束,从而将字典的最大似然估计转换成求解最优化问题。根据式(10)和式(5)可以完成字典D的学习以及稀疏表示s的求解。 在信号处理过程中经常将一个较长信号分割成若干固定长度信号段。在分割过程中,时间序列中的特征模式会由于信号段长度的不同而被“移动”到信号段内的不同时间位置。由于稀疏编码将时间序列表示成基函数的加权和,而为了表示被移动的特征模式,就必须在字典中构造同一基函数在不同时间位置的若干实例。然而,同一基函数在不同时间位置的实例仍然对应于同一信号事件。因此,需要引入移不变稀疏编码算法来解决同一基函数在不同时间位置的实例仍对应相同事件的难题。 移不变稀疏编码模型通过在原稀疏编码模型中引入附加参数来满足其“移不变”的特性: (11) 式中:Tl为移位算子,将基函数在位置范围l∈[-L,L]内移动;sk,j是移动到位置l处的基函数dk的系数;向量ε仍旧假设为高斯噪声。 移不变稀疏编码的系数求解与字典学习算法可从标准稀疏编码的对应算法得到。给定有限数据集X={x1,x2,…,xN},并假设基函数服从均匀分布,基函数与其对应系数的最大后验概率估计器为: (12) Subject to C (13) 式中,卷积算子 *是式(11)中移位算子Tl的一个特例;sk,j∈RM-K+1是基函数dk在信号xi中的稀疏激活;C定义了一个约束,防止求解的dk太大而sk,j太小。当设定变量d不变时,可以基于凸优化方法求解s,同理,当设定变量s不变时,可基于凸优化求解d。字典学习可通过迭代地交替求解这两个问题来实现;当目标函数收敛后,基于学习的基函数可求得稀疏解[15]。 从信号处理角度来讲,稀疏编码受益于字典学习来保证稀疏表示的稀疏性。通过字典学习,信号的特征模式被基函数捕捉;然后通过系数求解将信号中以一段时间序列表示的特征模式代之以一个非零系数表示,从而构成原信号的稀疏表示。因此,从理论上讲,稀疏编码可以作为设备状态监测中的一种有效特征提取方法。下面以轴承故障数据为例,验证稀疏编码在振动信号分析中的可行性。 振动数据取自美国凯斯西储大学(Case Western Reserve University, CWRU)的开放数据集[16]。该数据集被国内外基于状态维护的学者广泛使用,被认为是测试和验证设备状态识别新方法的一个基准。轴承试验装置示意如图1所示。左侧是一个2 HP的三相感应电动机(型号:Reliance Electric 2HP IQPreAlert),右侧是用于产生额定负载的测力计,二者通过扭矩传感器自动对准配合,测试轴承安装在电机驱动端,振动传感器安装在电机的驱动端上侧。 图1 轴承试验装置示意图 为了模拟轴承故障,分别在轴承的内圈、外圈(6∶00, 3∶00,12∶00方向)及滚动体上采用电火花加工的方式引入单点缺陷。缺陷尺寸分别为0.007、0.014、0.021、0.028 英寸,其中前三种尺寸采用SKF6205-2RS JEM型轴承,最后一种尺寸采用NTN 轴承。分别在0、1、2、3 hp 四种负载下获取振动数据,采集频率取12 kHz。 表1 轴承正常状态振动数据列表 轴承正常状态下采集的信号如表1所示,不同故障状态下采集的振动数据如表2所示。为了便于信号分析,每种轴承状态下的振动数据被分割成包含1 024个采样点的数据样本,并对数据样本边缘做光滑处理以减少信号分析中边缘效应。经过数据分割,表1中每种工况下的正常数据样本为236个,表2中不同工况及故障类型下的数据样本为128个,共计8024个数据样本。不失一般性地,负载为0 hp的正常及不同故障类型下的样本数据中随机抽取一半用于振动数据字典学习,所抽取数据样本标号末尾以“†”符号标记,剩余数据样本标号末尾以“”符号标记。 表2 故障状态下的轴承振动数据列表 从机械诊断学角度讲,瞬时振动脉冲波动携带了重要的诊断信息,是设备状态识别的重要依据。因此,捕捉和分析瞬时振动脉冲是振动信号处理和特征提取的目的之一。如果能够通过字典学习出振动信号中的瞬时脉冲作为基函数,无疑会促进稀疏编码对振动信号的特征提取。分别对表1与表2所抽取的振动样本数据(末尾以“†”符号标记)进行字典学习。指定基函数长度为80,每个字典中基函数个数为10。考虑到信号分割瞬时脉冲可能出现在信号段内的任意位置,采用基于移不变稀疏编码模型算法[14]进行字典学习,并进行稀疏求解。所学习出的振动信号字典如图2所示,从每一类振动数据中学习出的10个函数被标记为子字典Di(i∈[1,15]) 图2 从每一类轴承振动数据中学习出的字典(图中每一个子字典Di,从对应的数据样本学习得到) 图3 原始振动信号及其时域频谱图 从图2可以看出:从轴承正常状态振动数据中学习出的基函数明显有别于从故障状态振动数据中学习出的基函数,且没有明显的剧烈瞬时脉冲;从内外圈故障振动数据学习到的基函数波形比球故障振动数据的基函数波形更集中一些。这些不同可以从脉冲产生的机理来解释: (1) 轴承在正常状态下,滚动体在内外圈包围的滚道内平稳滚动,没有冲击产生。因而,轴承正常状态下的振动信号无明显的瞬时脉冲波动,但可能存在轴承刚性非线性、不同滚动体承载非线性或电机其他干扰源等因素,故会有均匀的微弱振动脉冲产生; (2) 当内圈或外圈出现损伤时,均匀排列的滚动体在滚道内滚动过程中会依次循环撞击损伤部位,因此,振动信号中会周期性地产生瞬时脉冲波动。 (3) 当损伤部位是在滚动体上时,每次损伤部位与内外圈滚道的撞击时间、撞击角度都是随机的,因此,振动信号虽然幅值较大,但无明显规律。不同轴承状态下的振动信号的波形特点决定了学习出的基函数具有不同的结构特点。 为了验证所学习出的字典的有效性,我们采用这些字典来求解振动信号的稀疏表示。不失一般性地,从内圈故障数据样本集I070中抽取一个信号样本进行稀疏表示的求解。该信号样本原始波形和时频谱如图3所示。采用从同类振动数据I070中学习出的字典Di求解该信号的稀疏表示,结果如图4所示。字典Di中的10个基函数依次竖直排列在图4中左侧,与之水平对应的右侧是各个基函数在原振动信号中的稀疏激活。稀疏激活中的每个尖峰表示对应的基函数在横轴所示的位置被激活,尖峰的幅值大小表示基函数的强度。由图4不难看到,稀疏表示中仅有少量的非零脉冲。 图4 基函数及其稀疏激活 根据式(1)所示的稀疏编码模型可知,一个原始振动信号可由基函数及其稀疏激活进行重构,结果见图5。对比图3和图5,不难看到:振动信号被很好的复原,时域波形上的瞬时脉冲更加突出,时频谱上的高频信号成分的周期性也更加明显。这一结果与稀疏编码模型中的高斯噪声假设有关,由于信号重构仅利用基函数与稀疏激活,假设噪声的成分被剔除,这在一定程度上起到了噪声抑制的作用。上述信号分析过程验证了从振动信号中学习出的字典有效性。 图5 重构振动信号及其时频谱图 上述稀疏编码算法以及针对振动信号的稀疏表示,可以直接用于基于状态的设备状态监控以及故障诊断。以美国凯斯西储大学公开的数据集为例,进行基于稀疏编码的人工轴承故障诊断实验分析研究。 将图4中基函数的稀疏激活取绝对值并在沿纵轴方向进行叠加,从而得到所有基函数在振动信号时间段内的激活统计,如图6所示。从图中下侧可以看到,在横轴方向上尖峰出现的位置对应于上侧的原始信号中的瞬时脉冲,并且其周期性更加明显。从稀疏激活的绝对值统计图中可以很容易地估计出脉冲出现的周期,经实际计算所得平均周期为0.006 2 s。这一周期对应着轴承内圈损伤时的通过频率162.2 Hz。 图6 基函数稀疏激活绝对值之和(内圈损伤) 图7 基函数稀疏激活绝对值之和(外圈损伤) 图8 基函数稀疏激活绝对值之和(滚动体损伤) 以上分析说明,稀疏编码在振动信号分析中的应用与常规的人工机械设备诊断方法相一致,从而进一步验证了稀疏编码可以作为一种有效的振动信号分析工具。 受设备维护人员凭借听觉系统所实现的生物本能诊断能力的启发,本文借鉴生物感知系统“冗余度压缩”的信息处理原则,引入神经科学研究中的稀疏编码算法,提出了连续长时间采样时振动信号有效特征提取方法。详细阐述了稀疏编码的理论背景、算法和模型,特别对稀疏编码相关的字典学习与稀疏表示求解进行了深入的分析总结。通过将稀疏编码应用于轴承振动信号分析,验证了其在挖掘振动信号中设备状态信息的有效性。基于人工轴承故障数据集进行的实验验证表明:基于稀疏编码的振动信号特征提取算法不仅能有效提取设备状态特征,而且稀疏特征具有良好的可分性。该方法可用于设备故障诊断,为基于状态的设备智能维护提供有效工具。 [1]Jardine A K S, Lin D, Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J]. Mechanical systems and signal processing, 2006, 20(7): 1483-1510. [2]Barlow H B. Possible principles underlying the transformation of sensory messages [J]. Sensory communication, 1961: 217-234. [3]Földiák P. Forming sparse representations by local anti-hebbian learning [J]. Biological cybernetics, 1990, 64(2): 165-170. [4]Olshausen B A. Emergence of simple-cell receptive field properties by learning a sparse code for natural images [J]. Nature, 1996, 381(6583): 607-609. [5]Olshausen B A, Field D J. Sparse coding of sensory inputs [J]. Current opinion in Neurobiology, 2004, 14(4): 481-487. [6]Smith E C, Lewicki M S. Efficient auditory coding [J]. Nature, 2006, 439(7079): 978-982. [7]尚丽.稀疏编码算法及其应用研究[D]. 合肥:中国科学技术大学, 2004. [8]刘海宁. 基于稀疏编码的设备状态识别及其重型轧辊磨床监测应用[D].上海交通大学,2011. [9]Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2009, 31(2): 210-227. [10]Davis G, Mallat S, Avellaneda M. Adaptive greedy approximations [J]. Constructive approximation, 1997, 13(1): 57-98. [11]Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries [J]. Signal Processing, IEEE Transactions on, 1993, 41(12): 3397-3415. [12]Pati Y C, Rezaiifar R, Krishnaprasad P. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]1993, IEEE. 40-44 vol. 1. [13]Lewicki M S, Sejnowski T J. Learning overcomplete representations [J]. Neural Computation, 2000, 12(2): 337-365. [14]Lewicki M S, Olshausen B A. Probabilistic framework for the adaptation and comparison of image Codes [J]. JOSA A, 1999, 16(7): 1587-1601. [15]Grosse R, Raina R, Kwong H, et al. Shift-invariant sparse coding for audio classification [J]. Cortex, 2007, 9: 8. [16]Loparo K, Bearings vibration data set[D]. Case Western Reserve University, 2003.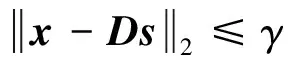
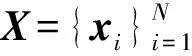
1.2 系数求解与字典学习
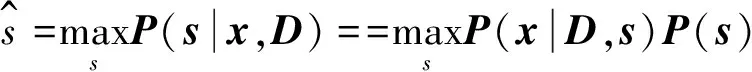
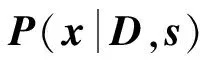
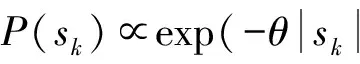
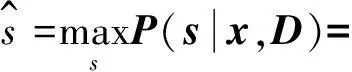

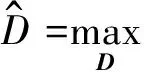
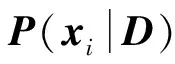
1.3 移不变稀疏编码
2 基于稀疏编码的振动信号分析
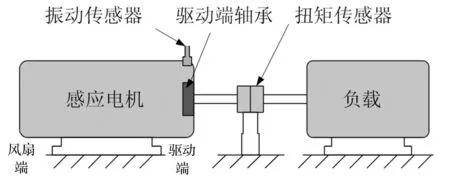
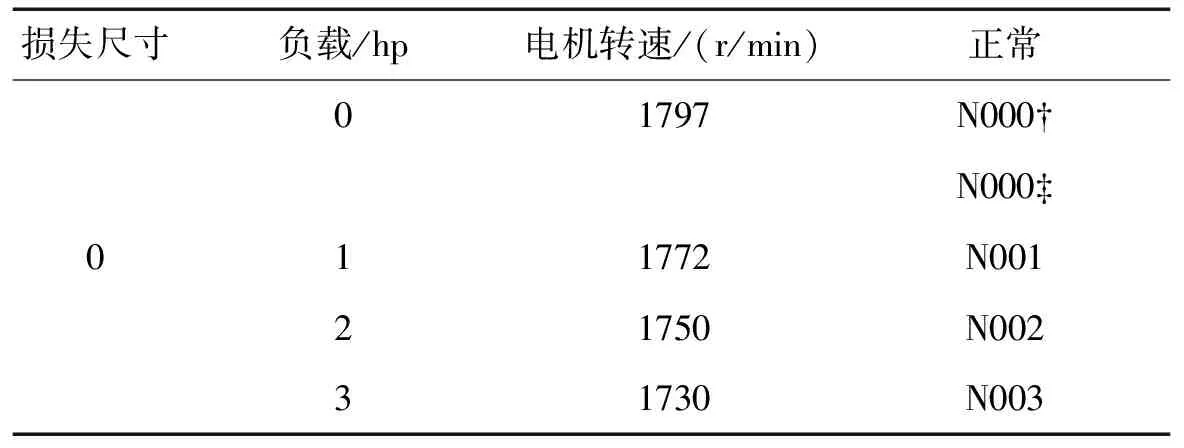
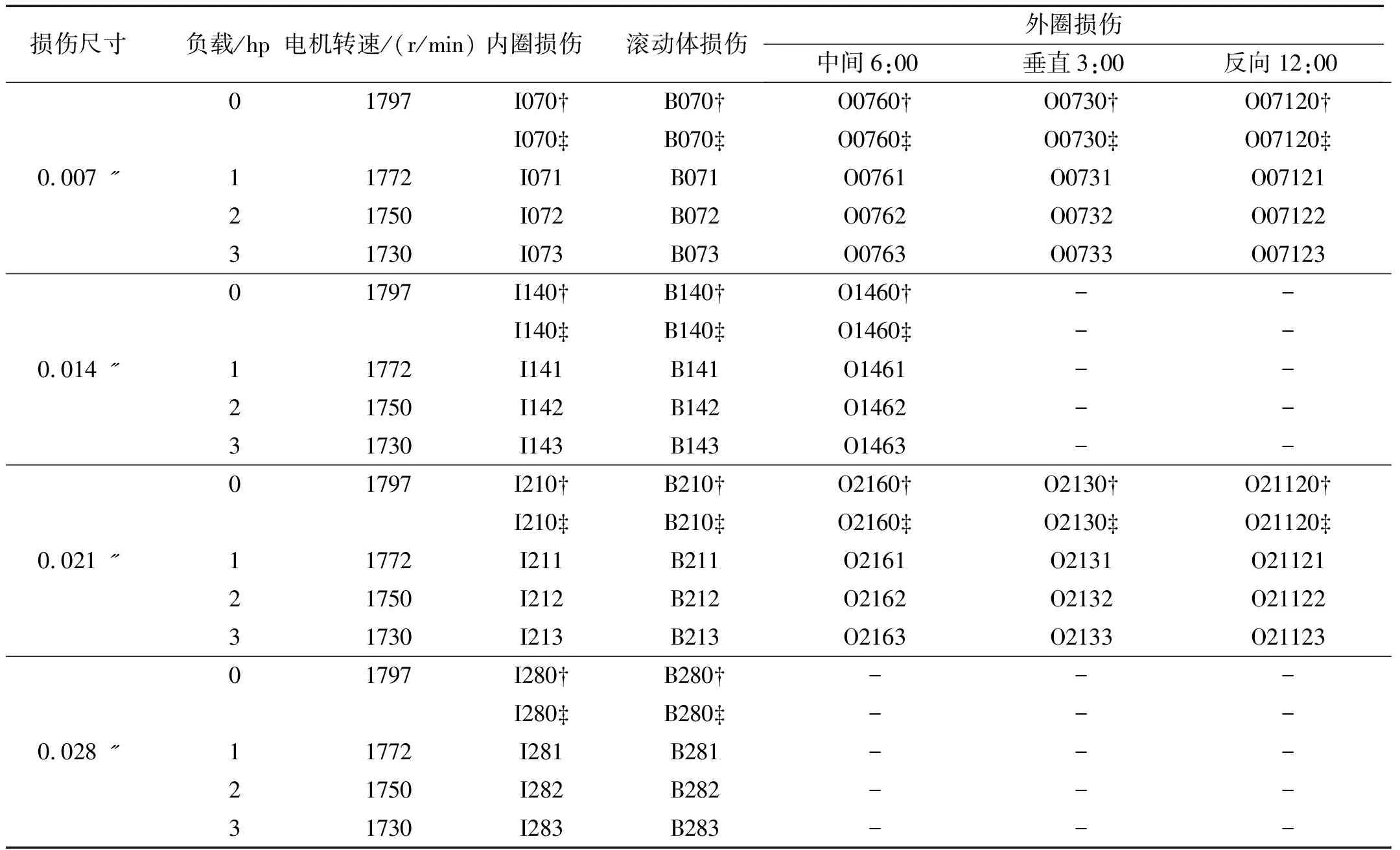
2.1 轴承振动数据获取
2.2 轴承振动信号字典学习
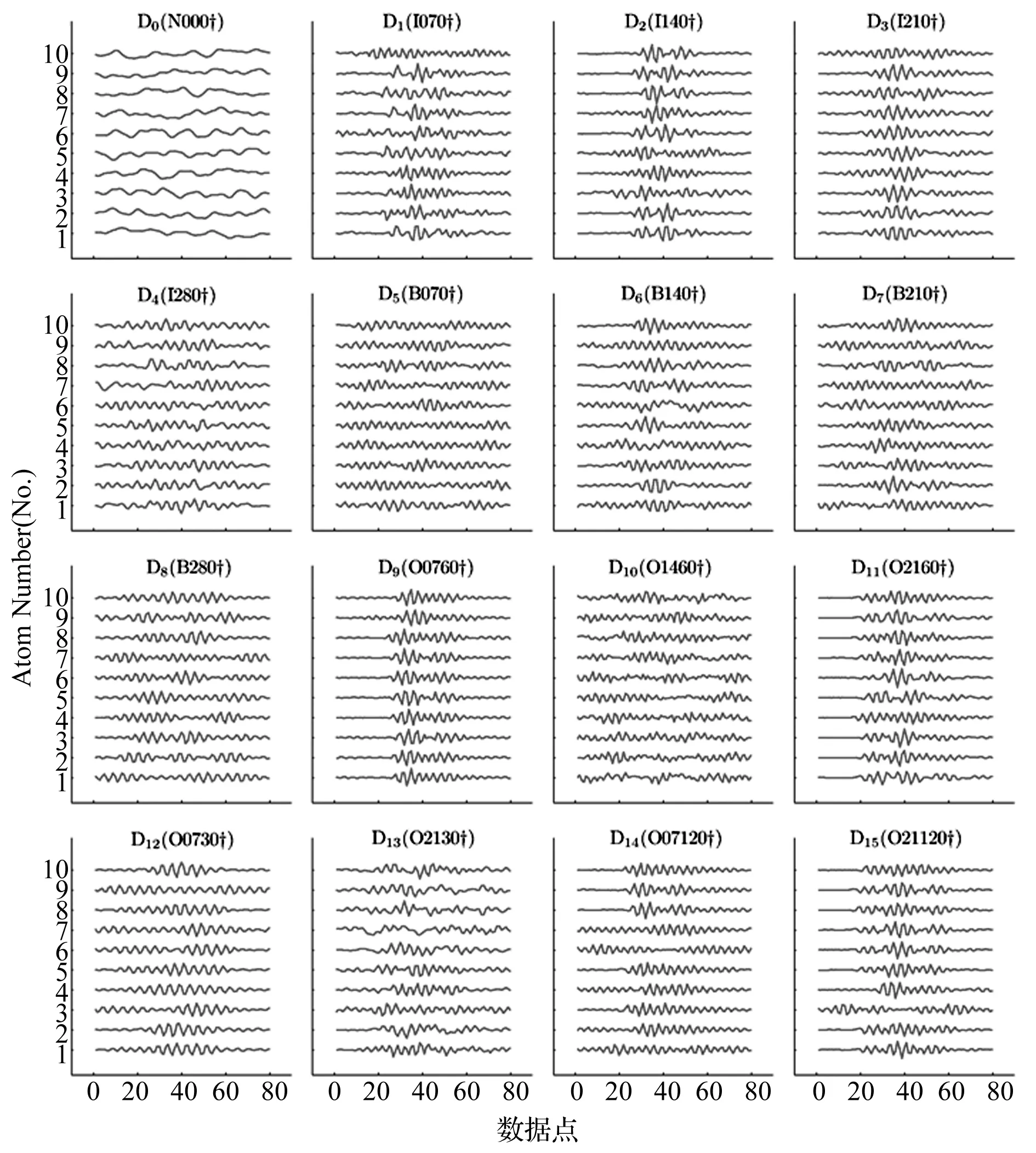
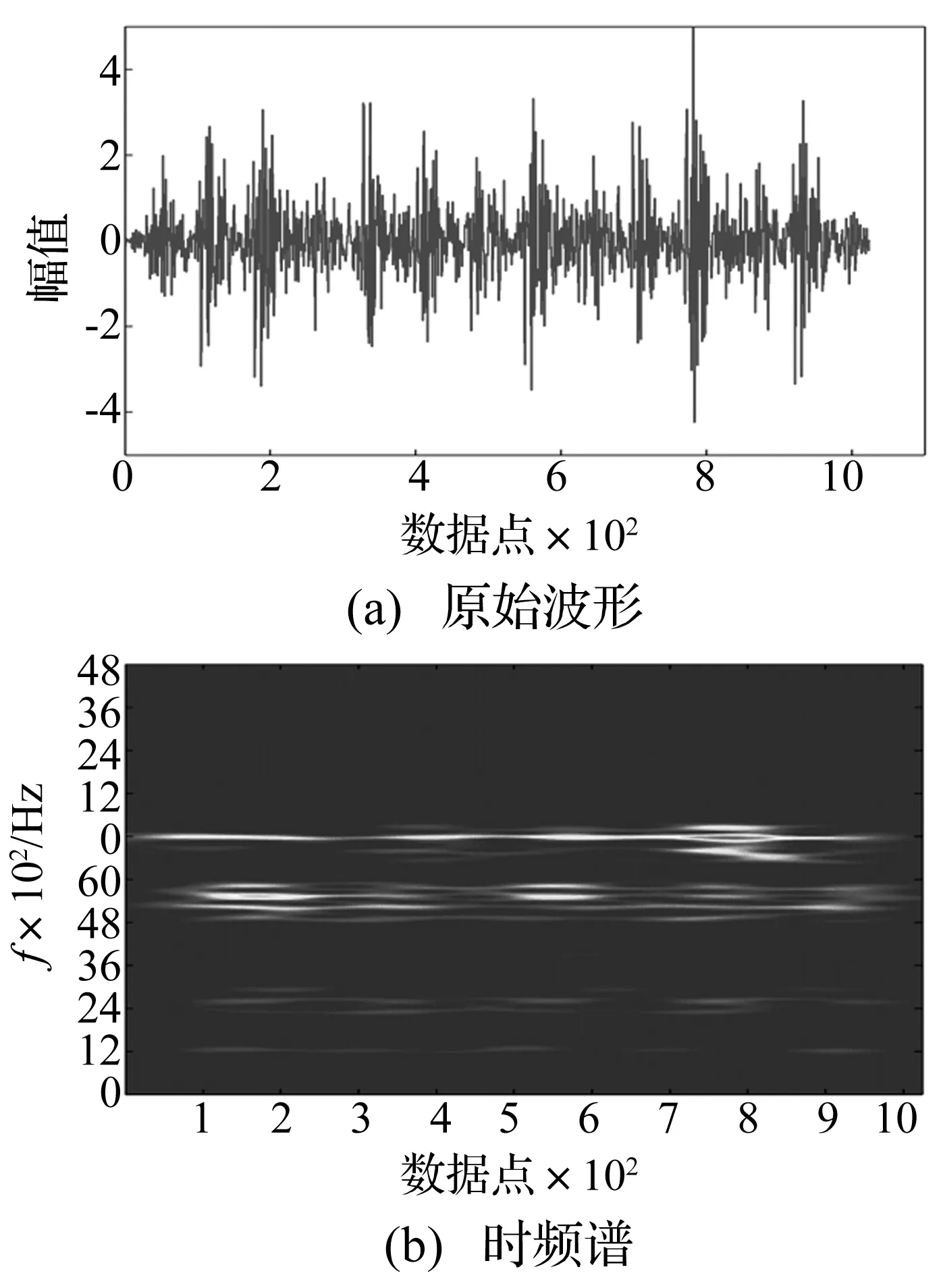
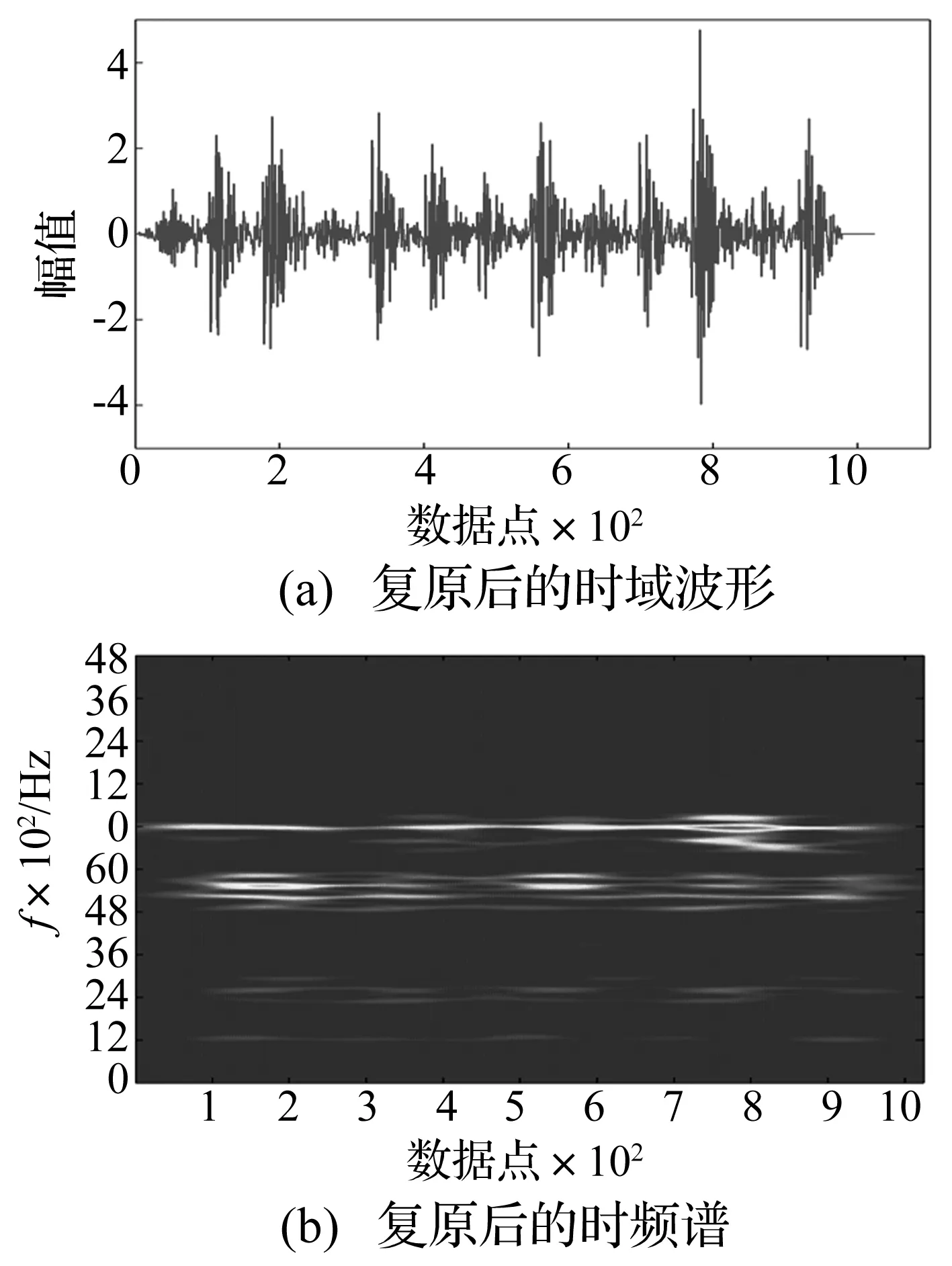
2.3 振动信号的稀疏编码分解与重构
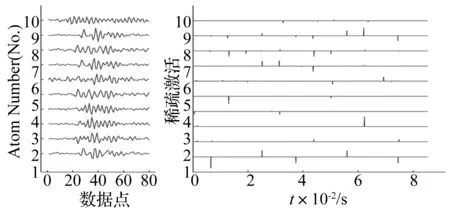
3 基于稀疏编码的人工轴承故障诊断实验研究
4 结 论

