基于最优扁平型结构元素长度的液压泵故障诊断研究
姜万录,郑 直,朱 勇,刘思远
(1. 燕山大学 河北省重型机械流体动力传输与控制重点实验室;2. 燕山大学 先进锻压成形技术与科学教育部重点实验室,秦皇岛 066004)
对液压泵进行故障诊断时,通常对泵壳的振动信号进行分析。但现场实测的振动信号会被采集设备等引入的噪声所干扰,导致信号失真。有效地从这些噪声干扰中提取液压泵的故障信息,可以为液压泵故障诊断提供良好的故障源信号[1-2]。
形态学滤波是在数学形态学变换的基础上发展起来的一种重要的非线性滤波工具[3]。对信号进行滤波时,利用起到滤波窗作用的结构元素作为“探针”,当信号局部特征和结构元素相匹配的时候,信息才会被保留下来,从而实现滤波[4]。结构元素长度过大,计算量就会增加,且导致过度滤波使信号细节信息被忽略;结构元素选择过小,噪声就不会被充分地抑制,有用的故障特征信息得不到充分的提取。所以,对起到滤波窗口作用的结构元素长度的选取对信号的滤波效果有着非常大的影响[5]。国内外学者对这一问题进行了深入的研究。Dong[4]根据不同长度扁平结构元素处理过的信号的信噪比作为优化条件,选取了最优结构元素长度。Zhang[6]根据“局部峰值”方法来优化三角形结构元素的长度和高度参数[6]。上述方法已成功地应用到了轴承故障的特征提取中。Zhang[7]利用遗传优化算法和BP神经网络来优化结构元素的长度。
Shannon[8]根据概率论和数理统计学的方法,第一次将“信息熵”的概念引入到信息论中,它是用来定量地描述信息的不确定性和复杂性。Yildiz等[9]利用脑电(EEG)信号提取小波系数能量熵作为自适应模糊推理系统模型的输入来评估大脑所处的状态。Sami[10]提取利用电流和电压信号的小波包能量熵作为ANN模型的输入来对故障进行定位。Yang[11]提取了滚动轴承振动信号的经验模态分解(EMD)能量熵,并利用ANN模型对其做了故障诊断分析。
本文将数学形态学和信息熵理论相融合,充分利用二者的优势,提出了一种基于形态学差值算子和功率谱熵理论相结合,并与特征能量比相配合的方法来确定最优扁平型结构元素长度以实现最优滤波。通过计算经过不同长度的滤波器滤波后的信号的功率谱熵值和特征能量比值,并根据功率谱熵的基本性质可得出最小功率谱熵值所对应的长度即为最优长度。通过仿真信号和实测液压泵故障信号的实验验证,结果表明该方法确定的最优扁平型结构元素长度的形态差值滤波器能够达到最优滤波效果。
1 数学形态学、功率谱熵和特征能量比
1.1 数学形态学基本变换
数学形态学是上世纪60年代由法国Matheron和Serra提出用来处理图像的理论,之后Maragos和Shafer将其扩展到对一维信号的滤波处理中[12-13]。
四种基本的形态学算子分别为:腐蚀、膨胀、开和闭。
若f(n)为一维原始离散信号,其定义域为F={0,1,2,…,N-1};g(m)为一维离散信号,称其为结构元素,其定义域为G={0,1,2,…,M-1},且M≪N。则f(n)关于g(m)的腐蚀和膨胀运算分别定义如下:
(fΘg)(n)=min{f(n+m)-g(m)}
m∈{0,1,2,…,M-1}
(1)
(f⊕g)(n)=max{f(n-m)+g(m)}
m∈{0,1,2,…,M-1}
(2)
f(n)关于g(n)的开和闭运算分别定义如下:
(f∘g)(n)=(fΘg⊕g)(n)
(3)
(f·g)(n)=(f⊕gΘg)(n)
(5)
1.2 差值滤波器
一维信号f(n)分别经过结构元素g(m)闭运算和开运算后的差值,称为差值滤波器,其表达式为:
DIF(f)=f·g(n)-f∘g(n)
(5)
上式可以分解为:
f·g-f∘g=(f·g-f)+(f-f∘g)
(6)
开运算和闭运算能根据实际信号中的波形轮廓形状的先验知识分别提取一维信号中的负、正脉冲。而差值算子则不需要先验知识而能同时提取正、负脉冲。因为f·g-f和f-f∘g正是形态学Top-Hat变换中的黑、白帽变换,而这两种变换就是用于提取信号中的负、正脉冲[6]。在本文中,利用该滤波器对液压泵故障信号进行滤波。
1.3 结构元素
形态学滤波的实质就是通过结构元素和待分析信号进行迭代形态学运算,从而达到滤波目的。所以结构元素的长度对于形态学滤波效果起到重要的作用。
常用到的结构元素有扁平型、三角型和半圆型等。三角型和半圆型结构元素具有长度和高度两个参数,分别适用于对脉冲噪声和随机噪声的滤除。而只有长度参数的扁平型结构元素具有计算简单、需要优化的参数少等优点,同时由于其高度为零,可避免对信号幅值的改变而获得了广泛的应用[14],所以本文采用扁平型结构元素。
1.4 功率谱熵
功率谱熵(PSE,Power Spectral Entropy)是在频域中对信号的一种不确定性和复杂性的描述,定义如下:
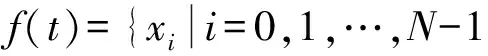
(7)
因此,把S视为整个频段的能量,那么s1,s2,…,sN是对信号总能量的N个分割,即信号的能量为S=s1+s2+…+sN。则定义频域中信号的功率谱熵为:
(8)

功率谱熵反映了信号在频域上的分布情况。从子带功率分布的角度定量地刻画了信号的不确定性和复杂性:子带能量分布越均匀,则信号不确定性和复杂性越高;反之则越低。
1.5 特征能量比
文献[15]定义了特征能量比为:
R=(E1+E2+…+En)/E
(9)
式中,E1、E2…En分别是信号经过消噪等处理后的1、2及n倍特征频率处的能量,E为取定频率段内的总能量。R越大,则在特征频率处的能量相对于取定频率段内总能量的比值越大,说明滤波效果越好[15]。
1.6 HF和R相结合确定结构元素最优长度
利用不同长度的扁平型结构元素对待分析信号进行滤波处理,对滤波后的信号进行HF的求取,结构元素长度的不同对应的HF值也是不同的。当HF值为最小时,根据定义可知:信号的子带谱线幅值在一定频率段内的分布最不均匀,不确定性和复杂程度最低。R的最大值说明:在特征频率处的谱线幅值相对于其它频率处的谱线幅值对这种不均匀分布的贡献最大,同时根据文献[15]也说明在最大R值点所对应的结构元素长度可以得到最优的滤波效果。所以,可以得出最小HF值点和最大R值点所对应的结构元素长度为最优滤波长度。
2 数值仿真算例
2.1 仿真信号
设计了如下的仿真信号进行分析:
x(t)=x1(t)+x2(t)+x3(t)
(10)
式中,x1(t)是频率为16 Hz的周期性指数衰减冲击信号,每周期内冲击函数为8e-100tsin(512πt);x2(t)是周期为20 Hz和40 Hz的叠加低频谐波干扰信号,x2(t)=cos(40πt)+cos(80πt);x3(t)是标准差为1的高斯白噪声,用于模拟强背景噪声。采样频率为2 048 Hz,采样时间为1 s。
仿真的目的是为了更好地抑制20 Hz和40 Hz处的叠加低频谐波和高斯白噪声的干扰,以提取冲击信号,并考察通过该方法确定的最优扁平型结构元素长度的滤波效果。
图1为混合信号的时域波形图和0-100 Hz低频段功率谱图。从图1(b)中可以看出冲击特征频率16 Hz及其倍频处的信号幅值几乎被噪声淹没,而在20 Hz和40 Hz处的低频谐波干扰信号的幅值很大。
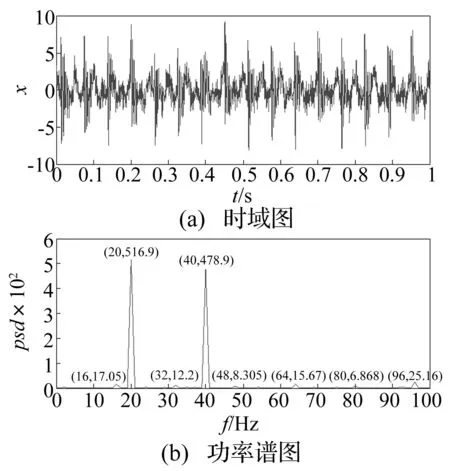
图1 混合信号
2.2 仿真结果分析
对仿真信号进行形态学差值运算,扁平型结构元素长度L的变化取为2到100。在求特征能量比R时,取冲击特征频率16 Hz的1-6倍频处的特征能量和0-1 024 Hz频率段的总能量进行运算。
图2为不同结构元素长度分别与功率谱熵值和特征能量比值的关系,横坐标为扁平结构元素的长度。
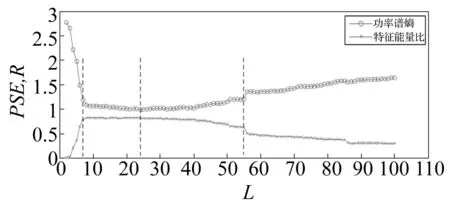
图2 PSE和R与结构元素长度的关系
如图所示,当2≤L≤7时,功率谱熵值随着L增加而快速递减。随着L的增加,在7≤L≤55区间的熵值变化比较平缓,其中在L=24时,熵值达到最小值0.985 8,两端点处的熵值分别为1.197和1.206,在L≥55区间的熵值随着L长度的增加而呈现相对快速的递增现象。对于特征能量比曲线,当2≤L≤7时,特征能量比值随着L增加而快速增加,在7≤L≤55区间的特征能量比值变化比较平缓,其中在L=24时,特征能量比R达到最大值0.822 8,两端点处的特征能量比R分别为0.777 6和0.622 7,在L≥55区间的熵值随着L长度的增加而呈现相对较快的递减现象。这说明最小功率谱熵值点与最大特征能量比值点是一致的。
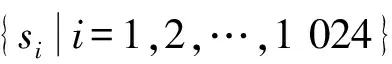
综上所述,可得出:在功率谱熵值比较小且变化缓慢的区域7≤L≤55,即L=(0.055-0.430)T(T为周期冲击长度:2 048 Hz/16 Hz=128个采样点)时能更好地滤除噪声,得到清晰故障特征信息,在功率谱熵值最小点所对应的L=24则是最优扁平结构元素长度。

图3 形态差值滤波器滤波后的信号功率谱图
图3分别是经过扁平型结构元素长度为7、24和55的形态差值滤波器滤波后的信号功率谱图。由图可知,在L=24时的滤波效果为最优,冲击特征频率16 Hz及其倍频处的幅值最大,低频谐波干扰信号20 Hz和40 Hz及噪声得到了有效的抑制。
3 液压泵故障信号分析
为了验证该方法的有效性,对某液压伺服故障模拟实验系统中的斜盘式轴向柱塞泵的振动信号进行采集并深入分析。
3.1 实验方法
液压泵的型号为MCY14-1B斜盘式轴向柱塞泵,柱塞数为7,额定转速为1 470 r/min,转轴频率为24.5 Hz。
在泵出口压力调定为15 MPa下,用50 kHz的采样频率分别采集滑靴磨损、中心弹簧磨损和松靴故障下的三组泵壳振动加速度信号,采集时间均为0.8 s。它们的故障冲击特征频率分别为171.5 Hz、24.5 Hz和171.5 Hz[16-17]。
3.2 滑靴磨损故障分析
滑靴-斜盘滑动摩擦副是轴向柱塞泵的三大摩擦副中最为复杂的一对[18]。当滑靴出现磨损故障时,故障滑靴对斜盘的冲击会增大。
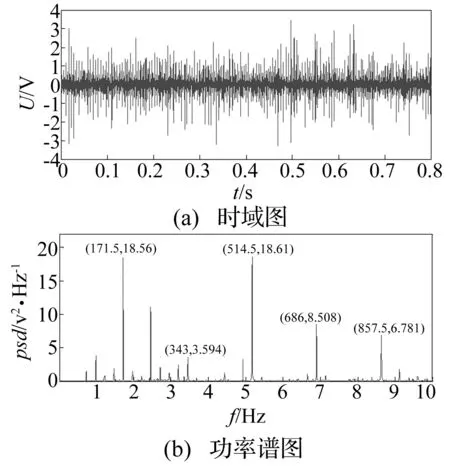
图4 滑靴磨损故障信号
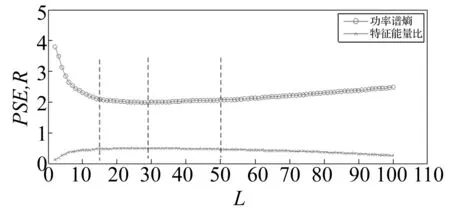
图5 PSE和R与结构元素长度的关系
图4(b)展示出了在故障冲击特征频率171.5 Hz及其倍频处的幅值特征。由于噪声的污染,在其它频率处的幅值也较高。
对滑靴磨损故障信号进行形态学差值运算,扁平型结构元素长度L的变化取为2到100。在求特征能量比R时,取故障冲击特征频率171.5 Hz的1~4倍频处的能量和0-25 kHz频率段的总能量进行运算。
分析过程如同2.2节,图5为不同结构元素长度与功率谱熵值和特征能量比值的关系。图中功率谱熵达到最小值1.986且特征能量比达到最大值0.499时所对应的结构元素长度为L=29。
在熵值比较小且变化缓慢的区域15≤L≤50(两端点处的熵值分别为2.082和2.062),即L=(0.051-0.171)T(T为滑靴故障周期冲击长度:50 000 Hz/171.5 Hz≈292个采样点)时能够更好地滤掉噪声,得到相对清晰的故障冲击特征信息,L=29则是最优扁平结构元素长度。
图6为L=29的形态差值滤波器对滑靴磨损故障信号进行滤波后的功率谱图。与图4(b)相比,故障冲击特征频率处的峰值得到了很好的凸现,噪声得到了很好的抑制。
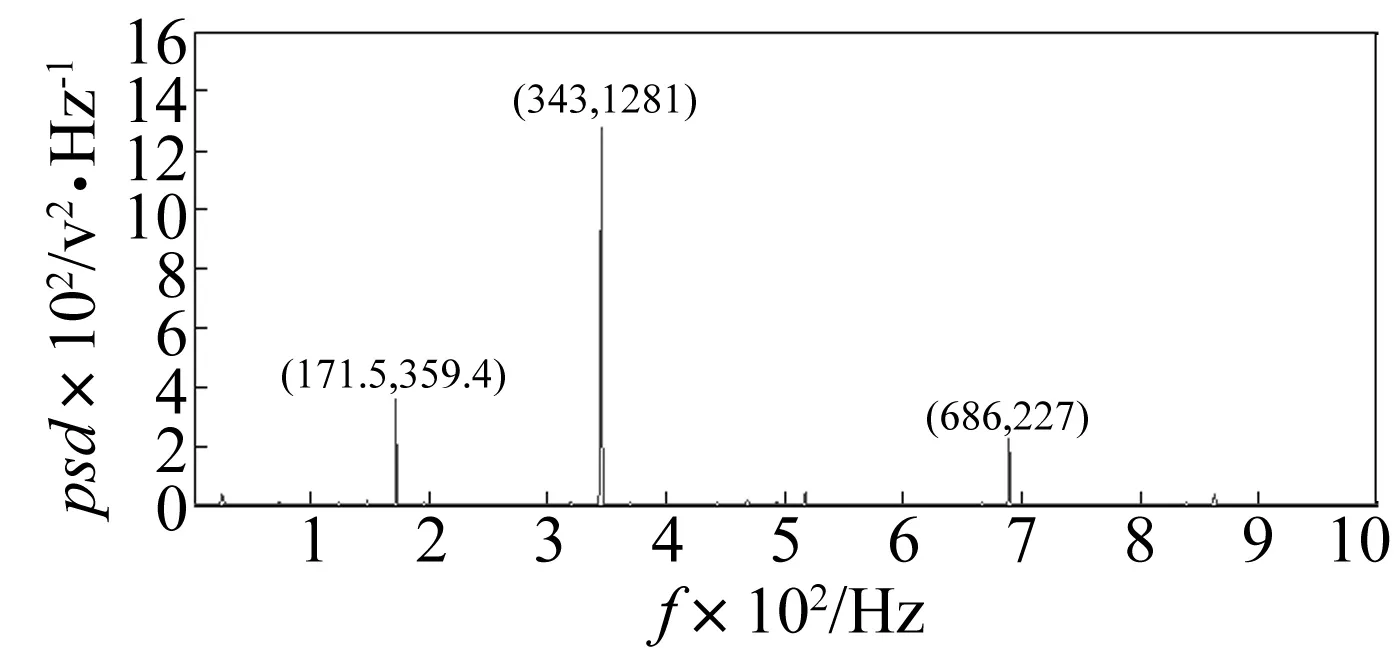
图6 滤波后的滑靴磨损故障信号功率谱图(L为29)
3.3 中心弹簧磨损故障分析
中心弹簧太短会导致柱塞回程不够、缸体-配流盘摩擦副的密封性能降低和内部油液的泄漏[18]。当中心弹簧出现磨损故障时,滑靴会加大对斜盘的冲击。
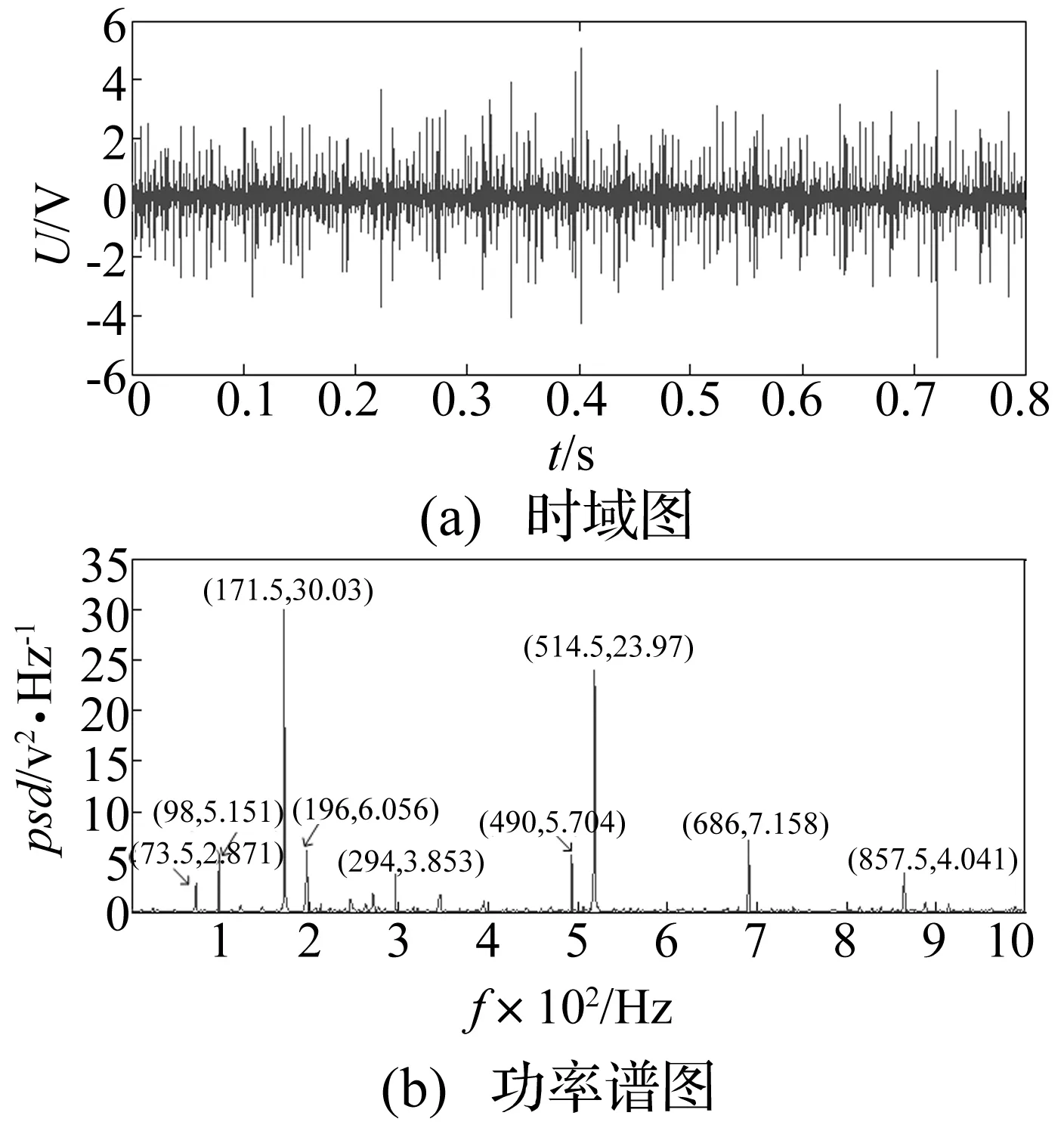
图7 中心弹簧磨损故障信号
图7(b)中展示出了在故障冲击特征频率24.5 Hz的某些倍频处的幅值特征,由于噪声的污染,在其它频率处也存在峰值。
对中心弹簧磨损故障信号进行形态学差值运算,扁平型结构元素长度L的变化取为2到180。在求特征能量比R时,取故障冲击特征频率24.5 Hz的1-25倍频处的能量和0-25 kHz频率段的总能量进行运算。
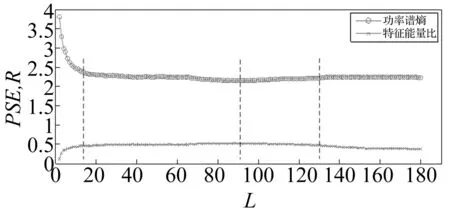
图8 PSE和R与结构元素长度的关系
分析过程如同2.2节,图8为不同结构元素长度与功率谱熵值和特征能量比值的关系。图中功率谱熵达到最小值2.157且特征能量比达到最大值0.525 3时所对应的结构元素长度为L=91。
在熵值比较小且变化缓慢的区域13≤L≤130(两端点处的熵值分别为2.383和2.219),即L=(0.006-0.064)T(T为中心弹簧磨损周期冲击长度:50 000 Hz/24.5 Hz≈2 041个采样点)时能够更好地滤掉噪声,得到相对清晰的故障冲击特征信息,L=91则是最优扁平结构元素长度。
图9为L=91的形态差值滤波器对中心弹簧磨损故障的信号进行滤波后的功率谱图。与图7(b)相比,故障冲击特征频率处的峰值得到了很好的凸现,噪声得到了很好的抑制。
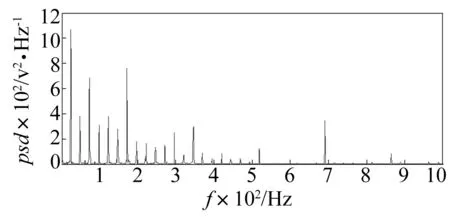
图9 滤波后的中心弹簧磨损故障信号功率谱图(L为91)
3.4 松靴故障分析
滑靴松动严重时会导致滑靴脱节或使活塞颈部扭断[18]。当发生此故障时,故障滑靴对斜盘的冲击增大。
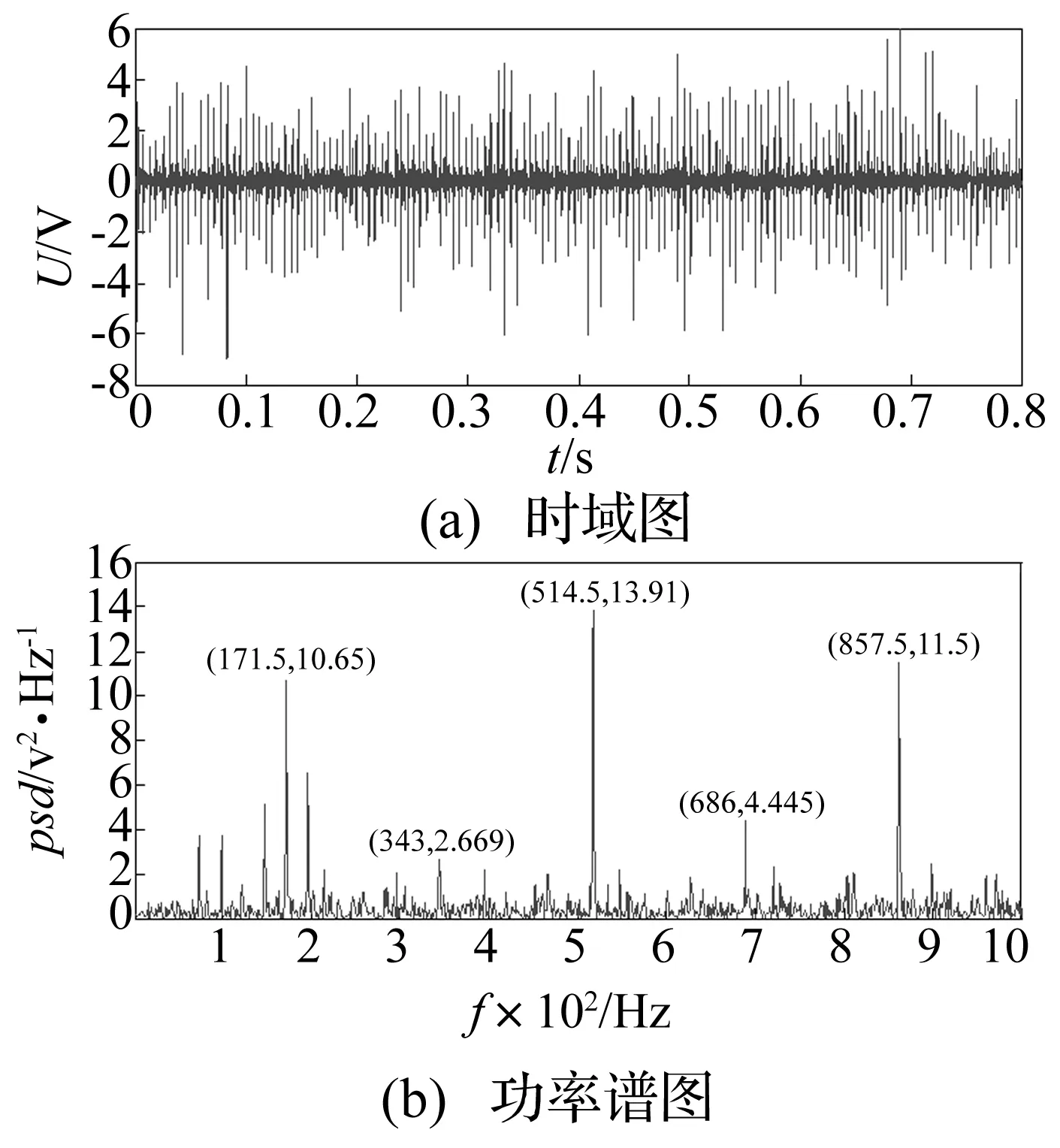
图10 松靴故障信号
图10(b)展示出了在故障冲击特征频率171.5 Hz及其倍频处的幅值特征,由于噪声的污染,其它频率处的幅值也很大。
对松靴故障信号进行形态学差值运算,扁平型结构元素长度L的变化取为2到100。在求特征能量比R时,取故障冲击特征频率171.5 Hz的1-5倍频处的能量和0-25 kHz频率段的总能量进行运算。
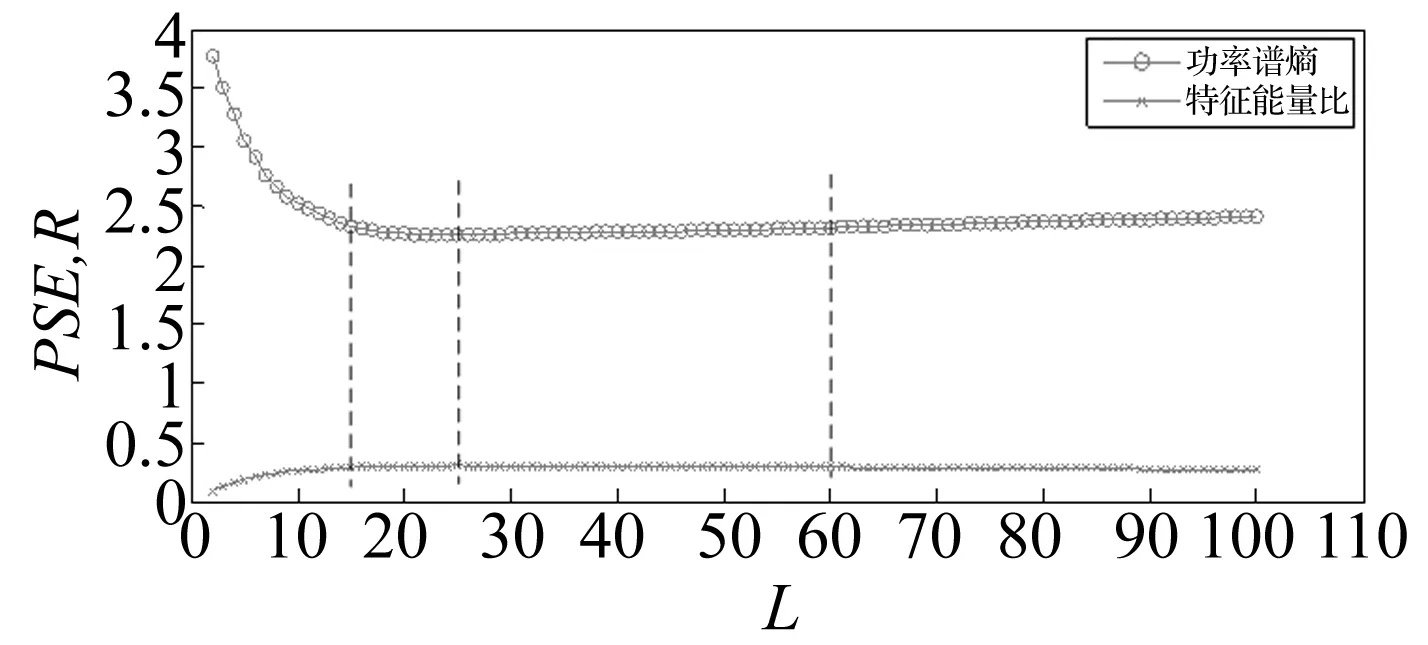
图11 PSE和R与结构元素长度的关系
分析过程如同2.2节,图11为不同结构元素长度与功率谱熵值和特征能量比值的关系。图中功率谱熵达到最小值2.256且特征能量比达到最大值0.308时所对应的结构元素长度为L=25。
在熵值比较小且变化缓慢的区域15≤L≤60(两端点处的熵值分别为2.333和2.32),即L=(0.051-0.205)T(T为松靴故障周期冲击长度:50 000 Hz/171.5 Hz≈292个采样点)时能够更好地滤掉噪声,得到相对清晰的故障冲击特征信息,L=25则是最优扁平结构元素长度。
图12为L=25的形态差值滤波器对松靴故障信号进行滤波后的功率谱图。与图10(b)相比,故障冲击特征频率处的峰值得到了很好的凸现,噪声得到了很好的抑制。
4 结 论
针对实测振动信号易受噪声污染而淹没有用信息和克服利用数学形态学对一维信号进行滤波时结构元素长度选取的经验性和任意性,提出了一种基于形态学差值算子和功率谱熵理论相结合,并与特征能量比相配合的方法来确定最优扁平型结构元素长度以实现最优滤波,并得出以下结论:
(1) 对于滑靴磨损故障信号,结构元素长度为L=(0.051-0.171)T(T为滑靴磨损故障周期冲击长度:50 000 Hz/171.5 Hz≈292个采样点)时能提取清晰的故障特征信息,功率谱熵最小值所对应的长度L=29是最优扁平结构元素长度,能达到最优的滤波效果;
(2) 对于中心弹簧磨损故障信号,当结构元素长度为L=(0.006-0.064)T(T为中心弹簧故障周期冲击长度:50 000 Hz/24.5 Hz≈2 041个采样点)时能提取清晰的故障特征信息,功率谱熵最小值所对应的长度L=91是最优扁平结构元素长度,能达到最优的滤波效果;
(3) 对于松靴故障信号,当结构元素长度为L=(0.051-0.205)T(T为松靴故障周期冲击长度:50 000 Hz/171.5 Hz≈292个采样点)时能提取清晰的故障特征信息,功率谱熵最小值所对应的长度L=25是最优扁平结构元素长度,能达到最优的滤波效果。
[1]姜万录,张淑清,王益群. 液压泵故障的小波变换诊断方法[J]. 机械工程学报, 2001, 37(6): 34-37.
JIANG Wan-lu, ZHANG Shu-qing, WANG Yi-qun. Wavelet transform method for fault diagnosis of hydraulic pump[J]. Chinese Journal of Mechanical Engineering, 2001, 37(6): 34-37.
[2]姜万录,吴胜强. 基于SVM和证据理论的多数据融合故障诊断方法[J]. 仪器仪表学报, 2010, 31(8): 1738-1743.
JIANG Wan-lu, WU Sheng-Qiang. Multi-data fusion fault diagnosis method based on SVM and evidence theory[J]. Chinese Journal of Scientific Instrument, 2010, 31(8):1738-1743.
[3]Serra J. Morphological filter: an overview[J]. Signal Process, 1994, 38(4): 3-11.
[4]Dong Ya-bin,Liao Ming-fu. Fault diagnosis of rolling element bearing based on modified morphological method[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1276-1286.
[5]Nikolaou N G,Antoniadis A. Application of morphological operators and envelope extractions for impulsive-type periodic signals[J]. Mechanical Systems and Signals Processing, 2003, 17(6): 1147-1162.
[6]Zhang Li-jun,Xu Jin-wu,Yang Jian-hong. Multiscale morphology analysis and its application to fault diagnosis[J]. Mechanical Systems and Signal Processing, 2008, 22(3): 597-610.
[7]Zhang Yu-dong,Wu Len-an. Recursive structure element decomposition using migration fitness scaling genetic algorithm[J]. Advances in Swarm Intelligence, 2011, 6728: 514-512.
[8]Shannon C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1984, 27:597-610, 623-656.
[9]Yildiz A,Akin M, Poyroz M, et al. Application of adaptive neuro-fuzzy inference system for vigilance level estimation byusing wavelet-entropy feature extraction[J]. Expert Systems with Applications, 2009, 36(4): 7390-7399.
[10]Ekici S,Yildirim S,Poyraz M. Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition[J]. Expert Systems with Applications, 2008, 34(4): 2937-2944.
[11]Yang Yu,Yu De-jie,Cheng Jun-sheng. A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration, 2006, 294(1-2): 269 -277.
[12]Matagos P,Schafer R W. Morphological filters-Part I: Their set-theoretic analysis and relations to liner shift-invariant filters[C]. IEEE Transactions on Acoustics, Speech, and Signal Processing ASSP, 2008, 22(3): 597-610.
[13]Matagos P,Schafer R W. Morphological filters-Part II: Their Their relations to median, order-statistic, and stack filters[C]. IEEE Transactions on Acoustics, Speech, and Signal Processing ASSP, 2008, 22(3): 1170-1184.
[14]李兵,张培林,刘东升. 基于自适应多尺度形态梯度变换的滚动轴承故障特征提取[J]. 振动与冲击,2011, 30(10): 104-108.
LI Bing, ZHANG Pei-lin, LIU Dong-sheng. Feature extraction for roller bearing fault diagnosis based on adaptive multi-scale morphological gradient transform[J]. Journal of Vibration and Shock, 2011, 30(10): 104-108.
[15]沈路,周晓军,张文斌. 形态解调在齿轮故障特征提取中的应用[J]. 浙江大学学报, 2010,44(8): 1514-1519.
SHEN Lu, ZHOU Xiao-jun, ZHANG Wen-bin. Application of morphological demodulation in gear fault feature extraction[J]. Journal of Zhengjiang University: Engineering Science, 2010 , 44(8): 1514-1519.
[16]吴胜强. 核主元分析及证据理论的多域特征故障诊断新方法研究[D]. 秦皇岛: 燕山大学, 2012.
[17]姜万录,牛慧峰,刘思远. 免疫支持向量机复合故障诊断方法及试验研究[J]. 振动与冲击, 2011, 30(6): 176-212.
JIANG Wan-lu, NIU Hui-feng, LIU Si-yuan. Composite fault diagnosis method and its verification experiments[J]. Journal of Vibration and Shock, 2011, 30(6): 176-212.
[18]刘思远. 信息融合和贝叶斯网络集成的故障诊断理论方法及实验研究[D]. 秦皇岛: 燕山大学, 2010.

