Time-varying confidence interval forecasting of travel timefor urban arterials using ARIMA-GARCH model
Cui Qinghua Xia Jingxin
(Intelligent Transportation System Research Center, Southeast University, Nanjing 210096, China)
Time-varying confidence interval forecasting of travel timefor urban arterials using ARIMA-GARCH model
Cui Qinghua Xia Jingxin
(Intelligent Transportation System Research Center, Southeast University, Nanjing 210096, China)
To improve the forecasting reliability of travel time, the time-varying confidence interval of travel time on arterials is forecasted using an autoregressive integrated moving average and generalized autoregressive conditional heteroskedasticity (ARIMA-GARCH) model. In which, the ARIMA model is used as the mean equation of the GARCH model to model the travel time levels and the GARCH model is used to model the conditional variances of travel time. The proposed method is validated and evaluated using actual traffic flow data collected from the traffic monitoring system of Kunshan city. The evaluation results show that, compared with the conventional ARIMA model, the proposed model cannot significantly improve the forecasting performance of travel time levels but has advantage in travel time volatility forecasting. The proposed model can well capture the travel time heteroskedasticity and forecast the time-varying confidence intervals of travel time which can better reflect the volatility of observed travel times than the fixed confidence interval provided by the ARIMA model.
confidence interval forecasting; travel time; autoregressive integrated moving average and generalized autoregressive conditional heteroskedasticity (ARIMA-GARCH); conditional variance; reliability
The development of efficient methodologies for accurately forecasting travel time is an important issue for ITS. However, conventional travel time forecasting concentrates on forecasting travel time levels with a presumed homogeneous variance. The time-varying confidence interval forecasting of travel time has not attracted more concern until travel time reliability was emphasized recently for the uncertainty of travel time forecasts. The time-varying confidence interval forecasting of travel time is related to both travel time level forecasting and conditional variance forecasting.
The models for travel time level forecasting range from linear weighted regression[1-2], Kalman filtering[3], time series[4-5],k-nearest neighbors[6], neural networks[7-8]and support vector machine[9]to combined or hybrid models[8]. However, the development of approaches for forecasting the conditional variance of travel time has received rather limited attention. Van Lint et al.[7-8]used neural networks to model the conditional variance, but the neural networks are limited to online applications because the model trainning is time-consuming. Recently, the generalized autoregressive conditional heteroskedasticity (GARCH) model[10]was used for the short-term forecasting of urban traffic variability. The model concentrates on the underlying volatility dynamics for generating travel time and can be used to calculate the conditional variance.
To date, the autoregressive integrated moving average (ARIMA) model which is one of the most important time series has shown comprehensive advantages in both forecasting accuracy and online applications. However, in the ARIMA model, the variance is assumed to be constant, which does not conform to the actual situation that heteroscedasticity has been found in travel time data. As we know, the GARCH model can capture heteroscedasticity characteristics. Therefore, the ARIMA model and the GARCH model are combined in this paper to forecast the conditional means and the conditional variances of travel time for calculating the time-varying confidence intervals of travel time.
1 Proposed Model
The ARIMA model has been acknowledged as an efficient way for the short-term travel time level forecasting. Assuming that the estimated travel time seriesXtis stationary, the basic idea of the ARMA model for modeling the travel time series is that the current travel timeXtis a linear combination ofpterms of lagged travel times andqterms of lagged errors as
Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+
ut-θ1ut-1-θ2ut-2-…-θqut-q
(1)
where the constants (φ1,φ2,…,φp) are called the autoregressive coefficients;utis the residual at timet; the constants (θ1,θ2,…,θq) are the moving average coefficients. By introducing the backshift operatorBand definingBjXt=Xt-1, Eq.(1) can be simplified as
φ(B)Xt=θ(B)ut
(2)
whereφ(B)=1-φ1B-φ2B2-…-φpBpandθ(B)=1-θ1B-θ2B2-…-θqBq.
Due to the fact that the most travel time series are non-stationary, the process of the series difference is usually applied withXtreplaced by (1-B)dXt, wheredis the difference index ofXt. Thus, the ARIMA model can be defined as
(1-B)dφ(B)Xt=θ(B)ut
(3)
Once there is a significant heteroskedasticity of the residual seriesutgenerated by the ARIMA model, the GARCH model can be applied for capturing the heteroskedasticity. The GARCH (p,q) model[11]is defined as
ut=σtet
(4)
(5)
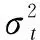
2 Model Validation
In this section, the travel time data used in this study are described, and the ARIMA-GARCH method is validated.
2.1 Data description
The travel time data used in this study were estimated from actual traffic flow data and intersection signal timing data collected by the traffic monitoring system of Kunshan city. Two arterial segments described in Tab.1 were selected as the research object. The travel time data from May 9, 2011 to May 13, 2011 were estimated at a 5-min interval in seconds. The travel time data on May 9, 2011 were used for model validation, and the others were used for model performance evaluation.
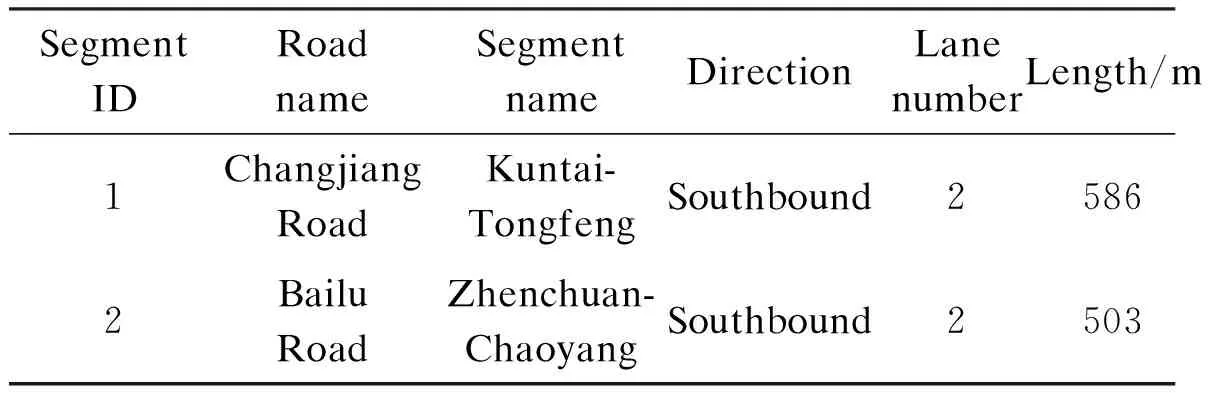
Tab.1 Segment description
2.2 Stationarity test for the travel time series
In this study, the ARIMA model is chosen as the travel time level forecasting model. The presumption of the ARIMA model is that the travel time series should be stationary or differenced to be stationary. Therefore, the unit root test based on the augmented Dickey-Fuller (ADF) approach is used. The test results show that original travel time series are non-stationary, but the first-order differenced travel time series are stationary. Therefore, the ARIMA model is suitable for the travel time level forecasting.
2.3 Constructing an ARIMA Model
In the ARIMA model process, it is essential to determine the lag order, which can be selected on the basis of the Bayesian information criterion the (BIC). In this study, the BIC values of the optimal ARIMA models are shown in Tab.2. Based on the BIC values, the optimal ARIMA model is determined as ARIMA(0,1,1) for the two urban arterial segments.

Tab.2 BIC values of the optimal ARIMA models
2.4 Residual autocorrelation test
Residual autocorrelation test is essential for checking whether the ARIMA model satisfies that the residual error series is white noise. The test results show that there is scarcely a notable autocorrelation in the residual error series, indicating that the ARIMA model is adequate for modeling the travel time series. However, the results show that autocorrelation clearly exists in its square series.
2.5 Testing the ARCH effect
The Lagrange multiplier (LM) test is chosen to verify the ARCH effect on the residual error series. Ann-th-order autoregression model is constructed for the squared residuals. The null hypothesis of the test is that there is no ARCH effect where autoregressive coefficients are equal to zero. Thep-value denotes the probability for accepting the null hypothesis. In this study, we construct a series of autoregression models withnfrom 1 to 5. The LM test results show that the null hypothesis is rejected when allp-values are equal to 0. Therefore, the GARCH model is adopted to forecast the conditional variances of travel time.
2.6 Constructing a GARCH Model
For constructing a GARCH model, the BIC is chosen to determine the lag order. The results are shown in Tab.3. The results show that the GARCH(1,1) model is optimal for modeling the travel time heteroskedasticity. Similarly, the LM test is applied to verify the effects of ARCH on the residuals generated from the ARIMA-GARCH model, and the results show that there is no ARCH effect. Therefore, an ARIMA(0,1,1)-GARCH(1,1) model can be constructed for the short-term forecasting of the mean and variance of travel time for urban arterials.

Tab.3 BIC values of the optimal GARCH models
3 Performance Evaluation
In this section, the proposed ARIMA-GARCH model and a comparative ARIMA model are used to predict the confidence interval of travel time on arterials from May 10, 2011 to May 13, 2011. Furthermore, performance measures are chosen to evaluate the proposed method and the comparative method.
3.1 Confidence interval forecasting
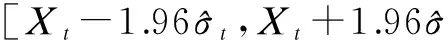
wtis the space between the upper and lower bounds of CI range at timet.
(6)
Taking segment 1 as an example, Fig.1 shows the forecasted CI width in the next four days. By comparison, we can find that the forecasted CI width using the ARIMA model is a constant, while it fluctuates when using the ARIMA-GARCH model. Moreover, we illustrate the forecasted CI range using the ARIMA-GARCH model and the ARIMA model with observed travel time on May 10, 2011 on segment 1, as shown in Figs.2 and 3. From the two figures, we can see that the observed travel times during the peak hours are more discrete than those of the off-peak hours. Consequently, the ARIMA-GARCH model proposes a larger confidence interval during fluctuating peak hours and a smaller confidence interval during off-peak hours, while the ARIMA model proposes constant confidence interval. Therefore, the forecasted CI ranges of the proposed model can better change with the volatility of observed travel times, indicating that the proposed method can better capture the dynamics of the real travel times. It can be used to improve the travel time forecasting reliability.

Fig.1 Forecasted CI width from May 10, 2011 to May 13, 2011
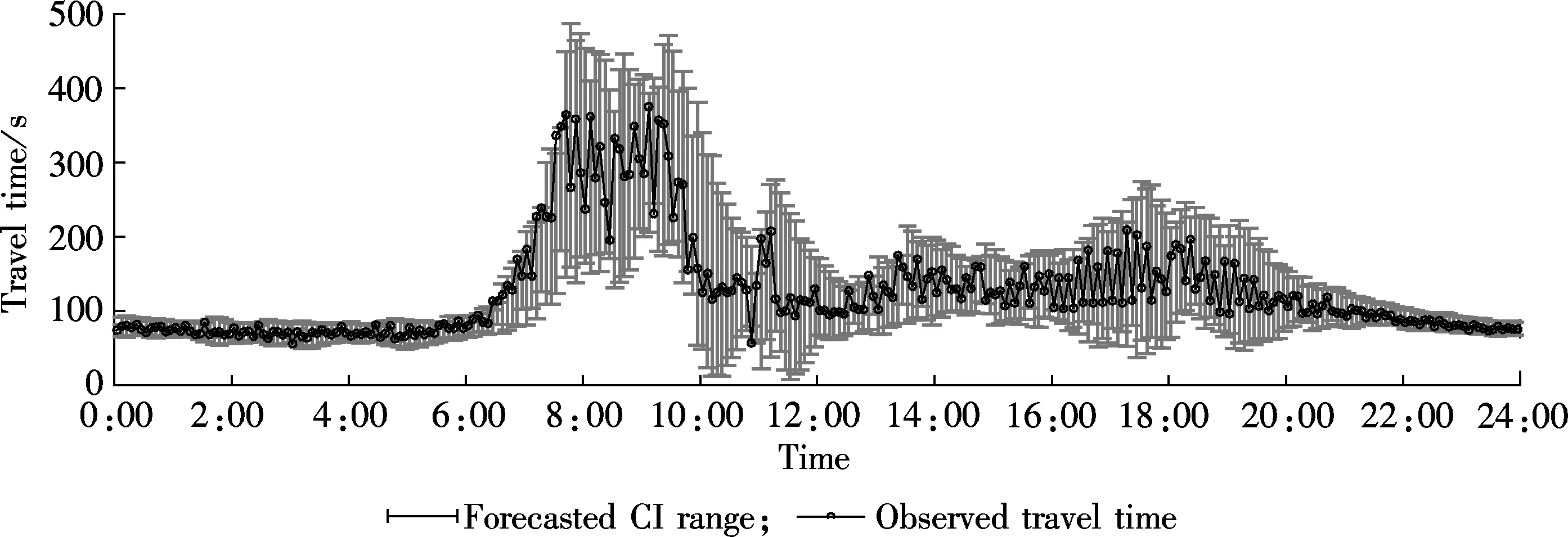
Fig.2 Forecasted CI range using ARIMA-GARCH model on May 10, 2011
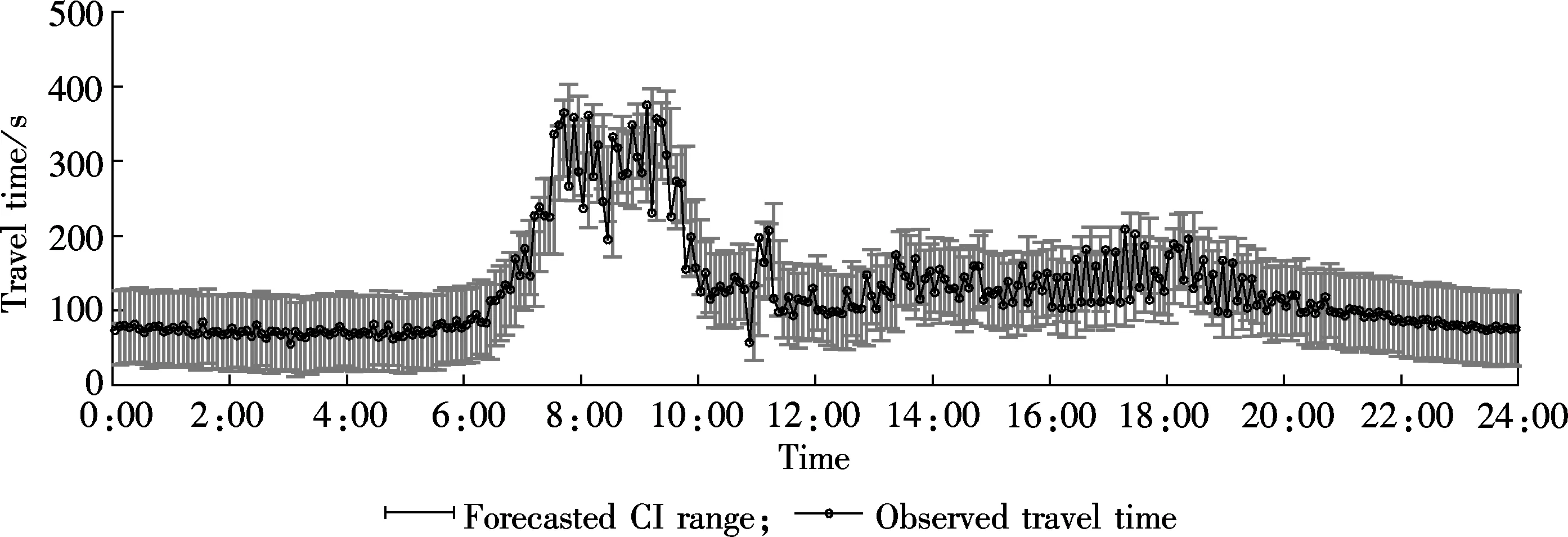
Fig.3 Forecasted CI range using ARIMA model on May 10, 2011
3.2 Forecasting performance
Root-mean-square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) are used to evaluate travel time level forecasting. The average CI width and hit rate which means the proportion of observed data points falling within the CI limit are used to evaluate travel time volatility forecasting.
Based on the evaluation data set, Tab.4 presents the forecasting performance of travel time using the ARIMA-GARCH model and the ARIMA model. The first three evaluation measures indicate that the ARIMA-GARCH model cannot significantly improve the forecasting performance of mean travel time. The reason is that the forecasts from the ARIMA-GARCH model are mainly determined by its mean equation. In other words, the heteroscedasticity has no significant influence on travel time level forecasting; however, it is reflected in the fluctuations of the forecasted confidence interval. The last two evaluation measures indicate that the confidence interval forecasted by the proposed model is more accurate in travel time volatility forecasting because it can produce a higher hit rate with a smaller average CI width than the ARIMA model. The reason of the superiority is that the forecasted CI ranges of the proposed model can better change with the volatility of observed travel times. In detail, during fluctuating peak hours, the proposed model produces a larger confidence interval to cover more actual observations while the ARIMA model produces a relatively smaller confidence interval which underestimates the actual volatility of travel time. During off-peak hours, the proposed model can produce a smaller confidence interval while the ARIMA model produces a relatively larger confidence interval which exaggerates the actual volatility of travel time.

Tab.4 Forecasting performance of travel time
4 Conclusion
In this paper, the time-varying confidence interval forecasting of travel time for urban arterials which can capture travel time uncertainty is analyzed using the ARIMA-GARCH model.
The results show that, although the improvement of forecasting accuracy of travel time levels brought by the proposed model is limited, its superiority is reflected in its travel time volatility forecasting. It can provide a series of time-varying confidence intervals of travel time, which can better change with the volatility of observed travel times and is more accurate than the fixed confidence interval provided by the ARIMA model. The time-varying confidence intervals of travel time can model both the evolution of travel time levels and the evolution of travel time volatility, so the proposed model can capture the characteristics of travel time more comprehensively and improve forecasting reliability.
[1]Rice J, Van Zwet E. A simple and effective method for predicting travel times on freeways[J].IEEETransactionsonIntelligentTransportationSystems, 2004, 5(3): 200-207.
[2]Du L, Peeta S, Kim Y H. An adaptive information fusion model to predict the short-term link travel time distribution in dynamic traffic networks[J].TransportationResearchPartB:Methodological, 2012, 46(1): 235-252.
[3]Liu H, Van Zuylen H, Van Lint H, et al. Predicting urban arterial travel time with state-space neural networks and Kalman filters[J].TransportationResearchRecord, 2006, 1968: 99-108.
[4]Yang M, Liu Y, You Z. The reliability of travel time forecasting[J].IEEETransactionsonIntelligentTransportationSystems, 2010, 11(1): 162-171.
[5]Ahmed M S, Cook A R. Analysis of freeway traffic time-series data by using box-jenkins techniques [J].TransportationResearchRecord, 1979, 722: 1-9.
[6]Myung J, Kim D K, Kho S Y, et al. Travel time prediction usingknearest neighbor method with combined data from vehicle detector system and automatic toll collection system[J].TransportationResearchRecord, 2011, 2256: 51-59.
[7]Khosravi A, Mazloumi E, Nahavandi S, et al. Prediction intervals to account for uncertainties in travel time prediction[J].IEEETransactionsonIntelligentTransportationSystems, 2011, 12(2): 537-547.
[8]Van Hinsbergen C P, Van Lint J W C, Van Zuylen H J. Bayesian committee of neural networks to predict travel times with confidence intervals[J].TransportationResearchPartC:EmergingTechnologies, 2009, 17(5): 498-509.
[9]Chen X, Gong H, Wang J. BRT vehicle travel time prediction based on SVM and Kalman filter[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2012, 12(4): 29-34. (in Chinese)
[10]Tsekeris T, Stathopoulos A. Real-time traffic volatility forecasting in urban arterial networks[J].TransportationResearchRecord, 2006, 1964: 146-156.
[11]Taylor S J.Modellingfinancialtimeseries[M]. Singapore:World Scientific Publishing, 2008.
基于ARIMA-GARCH模型的城市主干道行程时间时变置信区间预测
崔青华 夏井新
(东南大学智能交通系统研究中心, 南京 210096)
为了提高行程时间预测的可靠性,构建了自回归综合移动平均与广义自回归条件异方差性(ARIMA-GARCH)模型进行城市主干道行程时间动态置信区间预测,其中ARIMA模型作为GARCH模型的均值方程用于捕获行程时间均值,GARCH模型用于捕获行程时间条件方差.运用昆山市交通监测系统中采集的实际交通流数据进行验证和评估.结果表明,相较于传统的ARIMA模型,提出的方法虽然不能显著提升行程时间均值的预测性能,但是在行程时间波动性预测方面具有较大的优势.该方法可捕获行程时间异方差,从而能够预测出比ARIMA模型预测的固定置信区间更能反映行程时间观测值波动性的动态置信区间.
置信区间预测;行程时间;ARIMA-GARCH;条件方差;可靠性
U121
The National Natural Science Foundation of China (No.51108079).
:Cui Qinghua, Xia Jingxin. Time-varying confidence interval forecasting of travel time for urban arterials using ARIMA-GARCH model[J].Journal of Southeast University (English Edition),2014,30(3):358-362.
10.3969/j.issn.1003-7985.2014.03.019
10.3969/j.issn.1003-7985.2014.03.019
Received 2013-12-11.
Biographies:Cui Qinghua (1988—), female, graduate; Xia Jingxin(corresponding author), male, doctor, associate professor, jingxinxia@yahoo.com.cn.
 Journal of Southeast University(English Edition)2014年3期
Journal of Southeast University(English Edition)2014年3期
- Journal of Southeast University(English Edition)的其它文章
- P-FFT and FG-FFT with real coefficients algorithm for the EFIE
- Compressed sensing estimation of sparse underwateracoustic channels with a large time delay spread
- Improved metrics for evaluating fault detection efficiency of test suite
- Early-stage Internet traffic identification based on packet payload size
- An adaptive generation method for free curve trajectory based on NURBS
- Stability analysis of time-varying systems via parameter-dependent homogeneous Lyapunov functions
